欢迎关注个人主页：逸狼

---

创造不易，可以点点赞吗~

如有错误，欢迎指出~

---

---

目录

将递归转化为循环

逆波兰表达式

有效的括号

栈得压入、弹出系列

最小栈

---

将递归转化为循环

把递归代码实现为非递归代码

比如：逆序打印链表

<code>// 递归方式

void printList(Node head){

   if(null != head){

       printList(head.next);

       System.out.print(head.val + " ");

  }

}

// 循环方式

void printList(Node head){

   if(null == head){

       return;

  }

   Stack<Node> s = new Stack<>();

   // 将链表中的结点保存在栈中

   Node cur = head;

   while(null != cur){

       s.push(cur);

       cur = cur.next;

  }

逆波兰表达式

也叫后缀表达式（运算符在操作数的后面）,好处是：忽略运算符的优先级

我们平时运算加减乘除的式子其实是 中缀表达式 

比如式子a+b*c+(d*e+f)*g转成逆波兰表达式 abc*+de*f+g*+

逆波兰表达式的运算规则：

将操作数压入栈中遇到运算符弹出操作数（分别作为右操作数和左操作数）计算将计算的结果压入栈中

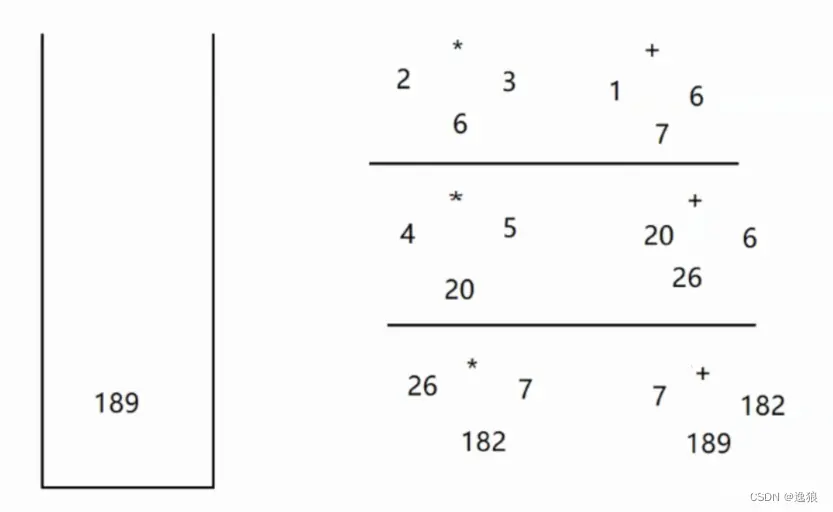
比如式子1+2*3+（4*5+6）*7

逆波兰表达式1 2 3*4 5*6 +7 *+

将1 2 3压入栈内，遇到*，取出2和3，计算2*3得6将6压入栈又遇到+，取出6和1，计算6+1得7

……

给你一个字符串数组 <code>tokens ，表示一个根据 逆波兰表示法 表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。oj链接

​

<code>class Solution {

public int evalRPN(String[] tokens) {

Stack<Integer> stack=new Stack<>();

for(int i=0;i<tokens.length;i++){

String tmp=tokens[i];

if(!isOperation(tokens[i])){

Integer val=Integer.valueOf(tmp);//将字符转化为整形

stack.push(val);

}else{

Integer val2=stack.pop();//val2作为右操作数

Integer val1=stack.pop();

switch(tmp){

case "+":

stack.push(val1+val2);

break;

case "-":

stack.push(val1-val2);

break;

case "*":

stack.push(val1*val2);

break;

case "/":

stack.push(val1/val2);

break;

}

}

}

return stack.pop();

}

//判断字符是否是 运算符

public boolean isOperation(String s){

if(s.equals("+")||s.equals("-")||s.equals("*")||s.equals("/")){

return true;

}

return false;

}

}

有效的括号

oj链接

​

括号匹配：栈最终为空，且字符串已经遍历完了

不匹配：

左括号与右括号不匹配    [ ( ] )字符串没有遍历完，遇到了右括号，但栈为空   (  )  ）））字符串遍历完，但栈里还有左括号（（（  ）右括号在前面 ）（（

<code>class Solution {

public boolean isValid(String s) {

Stack<Character> stack=new Stack<>();

for(int i=0;i<s.length();i++){

char ch=s.charAt(i);

if(ch=='('||ch=='['||ch=='{'){

stack.push(ch);

}else{

//遇到右括号

if(stack.empty()){

return false;//栈为空，没有左括号与之匹配

}else{

//取栈顶元素左括号 看与当前右括号是否匹配

char chL=stack.peek();

if(chL=='('&&ch==')'

||chL=='['&&ch==']'

||chL=='{'&&ch=='}'){

stack.pop();//说明当前这个括号匹配，所以要扔出去

}else{

return false;

}

}

}

}

return stack.empty();//如果循环走完，栈为空，返回真

}

}

栈得压入、弹出系列

oj链接

​

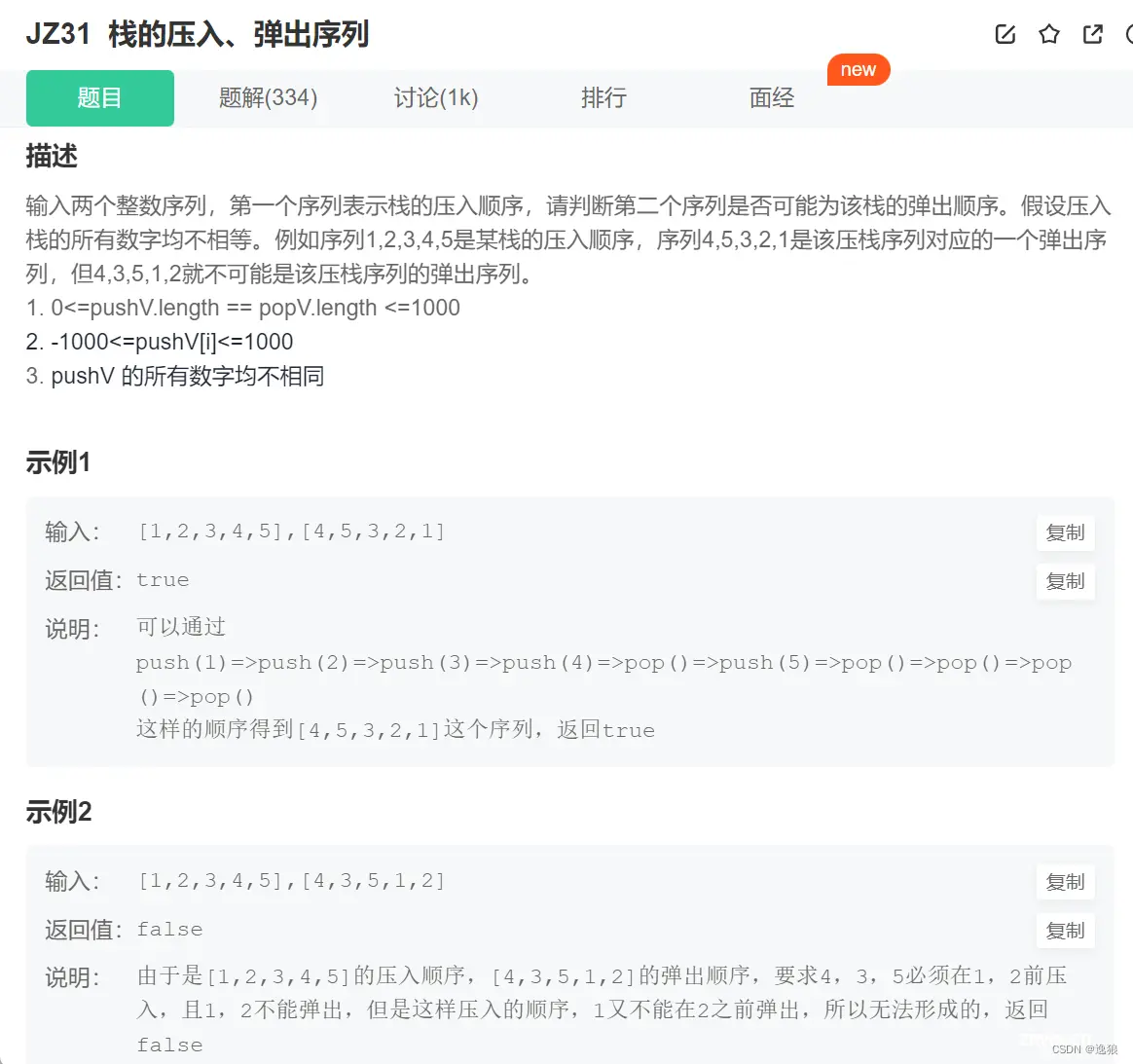
1. 遍历pushV数组，入栈，每次入栈后判断和popV数组的下标j是否一致

2.不一样,继续i++（继续进栈）；

一样,出栈，j++

3.出栈时，若一直一样就一直出，遇到不一样的，i++继续入栈；

注意：

j的条件：不能越界（超过popV的长度）栈不能为空<code>stack.peek()==popV[j] 引用类型时要用equals判断，这里为简单类型int.

public boolean IsPopOrder (int[] pushV, int[] popV) {

// write code here

Stack<Integer> stack=new Stack<>();

int j=0;

for(int i=0;i<pushV.length;i++){

stack.push(pushV[i]);

while(j<popV.length&&!stack.empty()&&

stack.peek()==popV[j]){

stack.pop();

j++;

}

}

return stack.empty();

}

}

最小栈

oj链接

​

 分别创建两个栈：普通栈 和 最小栈

push存放元素的过程：

如果是第一次存放元素，普通栈和最小栈都得存放元素；如果不是第一次存放，普通栈里放，需要比较的普通栈的栈顶元素和最小栈的，只有小于等于才能放入最小栈里。

pop取元素的过程（返回值是普通站的元素）：

每次pop元素时需要判断出栈的元素是不是和最小栈的栈顶元素一样，若一样，最小栈也得pop

top瞄一眼（相当于peek，返回的是普通栈的值）

getMin获取最小栈的栈顶元素

<code>import java.util.Stack;

class MinStack {

public Stack<Integer> stack;

public Stack<Integer> minStack;

public MinStack() {

stack=new Stack<>();

minStack=new Stack<>();

}

public void push(int val) {

stack.push(val);

if(minStack.empty()){

minStack.push(val);

}else{

Integer peekVal=minStack.peek();

if(val<=peekVal){

minStack.push(val);

}

}

}

public void pop() {

if (stack.empty()) {

return;

}

int popVal=stack.pop();

if(popVal==minStack.peek()){

minStack.pop();

}

}

public int top() {

if(stack.empty()){

return -1;

}

return stack.peek();

}

public int getMin() {

if(minStack.empty()){

return -1;

}

return minStack.peek();

}

}