目录

一、用户均衡模型简略介绍       

1.1 Wardrop第一原理

1.2 用户均衡模型

1.3 BPR函数 

1.4 用户均衡模型的积分项

 二、Frank Wolfe算法求解步骤

三、代码

3.1 导入必要的库

 3.2 构建交通网络

3.3 绘制交通路网图

3.4 定义BPR函数

3.5 初始化路网流量

3.6 获取 flow_temp

3.7 获取下降方向descent

3.8  定义目标函数

3.9 一维搜索最优步长，并更新流量

3.10 主函数

四、所用文件

---

CSDN公式加载有问题，读者可以尝试刷新，或者去知乎阅读（同名文章）。

如果对本博客有任何疑问，请转至知乎评论区：UE求解

一、用户均衡模型简略介绍       

1.1 Wardrop第一原理

 道路的利用者，都确切知道网络的交通状态，并试图选择最短路径当网络达到平衡状态时，每个OD对的各条被使用的路径，行驶时间相等，且行驶时间最短没有被使用的路径的行驶时间大于或等于最小行驶时间

1.2 用户均衡模型

        满足Wardrop第一原理的交通分配模型，称为用户均衡模型。

        1956年Beckmann提出了一种满足Wardrop第一原理的数学规划模型。模型核心是，交通网络中的用户，都试图选择最短路径，而最终使得被选择的路径的阻抗最小且相等。该数学规划模型为：

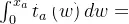
1.3 BPR函数 

        在用户均衡模型中，

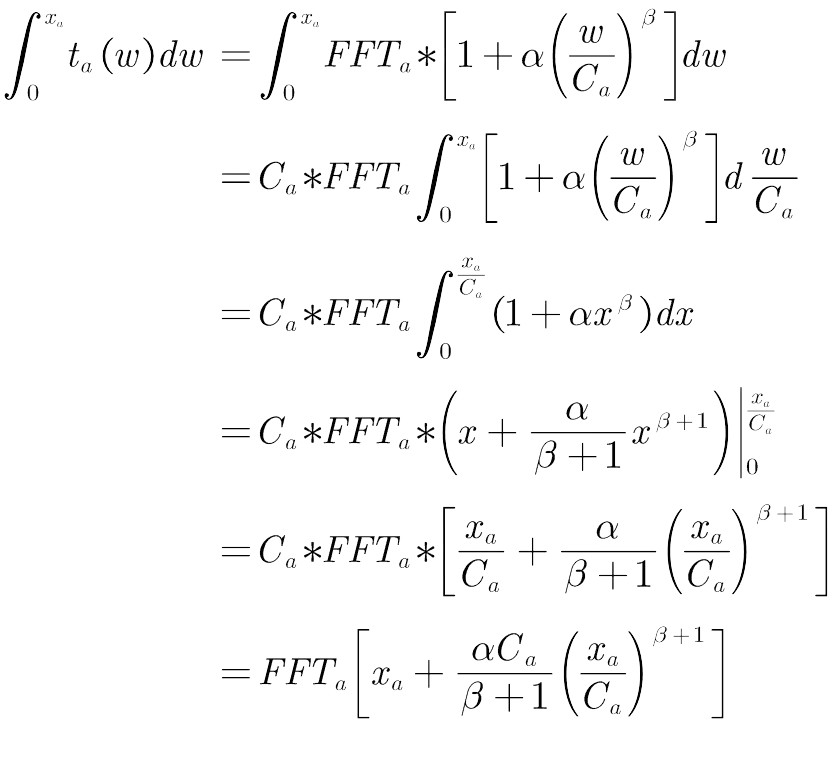
为路阻函数，我们一般采用BPR函数，即：

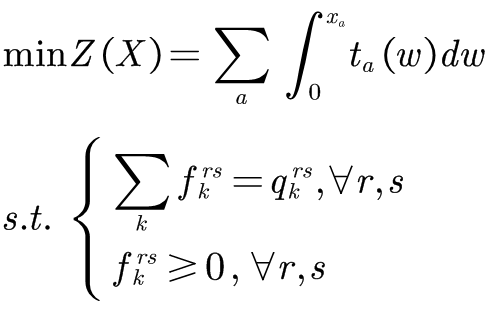
，表示最快通过路段a的时间；α常取0.15，β常取4.0 ；

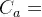
，表示路段a的通行能力；

，表示路段a的流量

1.4 用户均衡模型的积分项

        为便于后续求解，我们将BPR函数代入

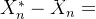
，进行积分计算，过程如下：

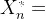
        因此，我们的目标函数为：

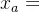
        当然，系统最优模型，是与用户均衡模型相通的。对于系统最优模型，其目标函数表达式为

 二、Frank Wolfe算法求解步骤

        友情提醒：后面若对代码主体逻辑有疑惑，返回看看这部分。

        步骤1：初始化。基于零流图的路阻，依次搜索每一个OD对 r,s 所对应的最短路径，并将 r,s 间的OD流量，全部分配到对应的最短路径上，得到初始路段流量

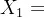
，并令迭代次数n=1。

        步骤2：更新路阻。根据BPR函数，分别代入每个路段的初始流量，求得阻抗

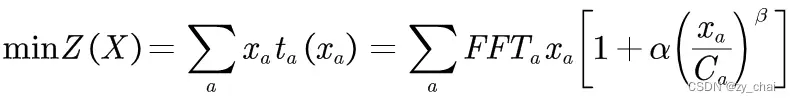
        步骤3：下降方向。基于阻抗

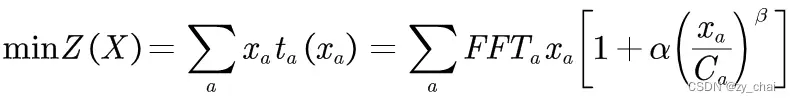
，按照步骤1中的方法（最短路全有全无分配），将流量重新分配到对应路径上，得到临时路段流量

，进而得到

        步骤4：搜索最优步长，并更新流量。采用二分法，搜索最优步长

，并令

。其中，最优步长满足：

        步骤5：结束条件。如果

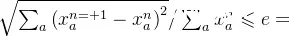
，则算法结束；否则n=n+1，转至步骤2。此处的e 表示误差阈值，在代码部分用max_err表示。

三、代码

        代码基于Python的NetWorkX库编写，这样将大大减少我们代码编写的工作量，并且更易于阅读。我们以SiouxFalls交通网络为例，进行交通网络构建与流量分配。

3.1 导入必要的库

import pandas as pdimport numpy as npimport networkx as nximport matplotlib.pyplot as pltfrom scipy.optimize import minimize_scalar pandas，用于读取文件；numpy在计算误差时使用；networkx贯穿整个代码；matplotlib用于绘制交通网络图scipy在搜索最优步长时用到。

 3.2 构建交通网络

def build_network(Link_path, Node_path): # 读取点数据、边数据 links_df = pd.read_csv(Link_path) # 需要注意使用from_pandas_edge，其读取的边的顺序和csv中边的顺序有差异 G = nx.from_pandas_edgelist(links_df, source='O', target='D', edge_attr=['FFT', 'Capacity'], create_using=nx.DiGraph()) nx.set_edge_attributes(G, 0, 'flow_temp') nx.set_edge_attributes(G, 0, 'flow_real') nx.set_edge_attributes(G, 0, 'descent') nx.set_edge_attributes(G, nx.get_edge_attributes(G, "FFT"), 'weight') # 获取节点位置信息 nodes_df = pd.read_csv(Node_path) node_positions = {} for index, row in nodes_df.iterrows(): node_positions[row['id']] = (row['pos_x'], row['pos_y']) # 更新图中节点的位置属性 nx.set_node_attributes(G, node_positions, 'pos') return G Link_path，表示路网文件路径。下载链接见文末，数据示例如下：

O	D	FFT	Capacity
1	2	6	25900.20064
1	3	4	23403.47319
2	1	6	25900.20064
2	6	5	4958.180928
3	1	4	23403.47319

Node_path，表示节点文件路径。下载链接见文末，数据示例如下：

id	pos_x	pos_y
1	2	2
2	13	2
3	2	5
4	5	5
5	9	5

flow_real，表示每次迭代更新后的路段流量或初始化流量，所有路段的flow_real组成

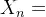
flow_temp， 所有路段的flow_temp组成

descent，表示flow_temp与flow_real的差值，所有路段的descent组成

weight，表示路阻。初始的路阻，由于路段流量都是0，所以直接用FFT。后续将用BPR函数计算

3.3 绘制交通路网图

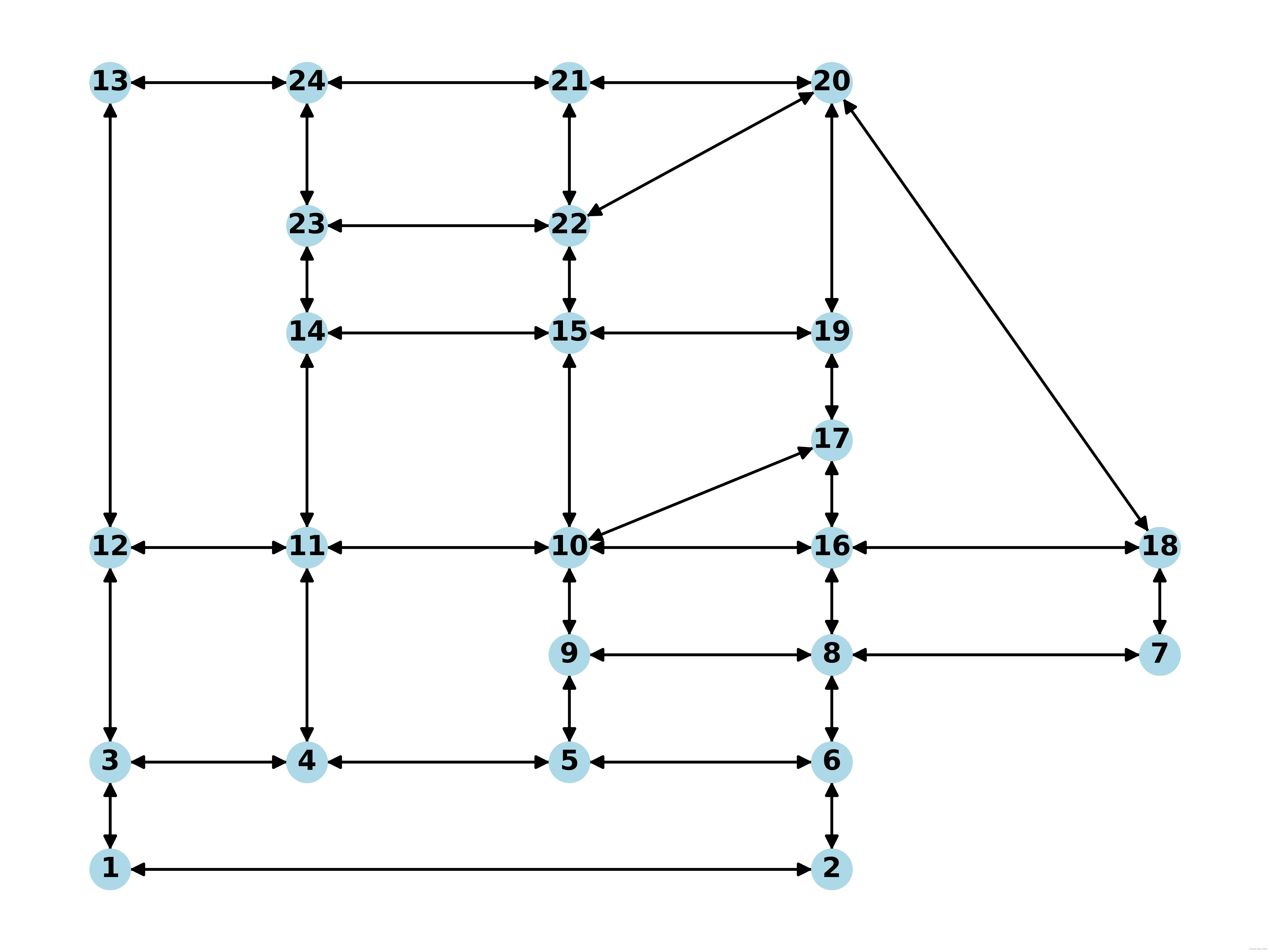
def draw_network(G): pos = nx.get_node_attributes(G, "pos") nx.draw(G, pos, with_labels=True, node_size=200, node_color='lightblue', font_size=10, font_weight='bold') plt.show()

         构建交通网络后，我们来看一看这个SiouxFalls网络长什么样子吧

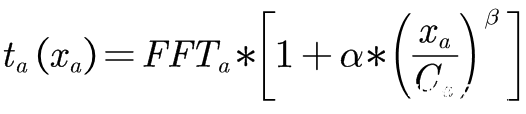
3.4 定义BPR函数

def BPR(FFT, flow, capacity, alpha=0.15, beta=4.0): return FFT * (1 + alpha * (flow / capacity) ** beta) FTT，表示最快通过时间；flow，表示路段流量；capacity，表示路段通行能力；alpha和beta，是BPR函数的参数，在此取默认值。

3.5 初始化路网流量

def all_none_initialize(G, od_df): # 这个函数仅使用一次，用于初始化 # 在零流图上，按最短路全有全无分配，用于更新flow_real for _, od_data in od_df.iterrows(): source = od_data["o"] target = od_data["d"] demand = od_data["demand"] # 计算最短路径 shortest_path = nx.shortest_path(G, source=source, target=target, weight="weight") # 更新路径上的流量 for i in range(len(shortest_path) - 1): u = shortest_path[i] v = shortest_path[i + 1] G[u][v]['flow_real'] += demand # 初始化流量后，更新阻抗 for _, _, data in G.edges(data=True): data['weight'] = BPR(data['FFT'], data['flow_real'], data['Capacity'])

        这个函数仅使用一次，用于初始化。在零流图上，按最短路全有全无分配，用于得到

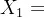
。 od_df表示pd.Dataframe数据格式的OD流量信息。ODParis.csv示例数据如下：

o	d	demand
1	2	100
1	3	100
1	4	500
1	5	200
1	6	300
1	7	500

3.6 获取 flow_temp

        flow_temp，即

def all_none_temp(G, od_df): # 这个是虚拟分配，用于得到flow_temp # 每次按最短路分配前，需要先将flow_temp归零 nx.set_edge_attributes(G, 0, 'flow_temp') for _, od_data in od_df.iterrows(): # 每次更新都得读OD，后面尝试优化这个 source = od_data["o"] target = od_data["d"] demand = od_data["demand"] # 计算最短路径 shortest_path = nx.shortest_path(G, source=source, target=target, weight="weight") # 更新路径上的流量 for i in range(len(shortest_path) - 1): u = shortest_path[i] v = shortest_path[i + 1] # 更新流量 G[u][v]['flow_temp'] += demand

3.7 获取下降方向descent

        descent，即

def get_descent(G): for _, _, data in G.edges(data=True): data['descent'] = data['flow_temp'] - data['flow_real']

3.8  定义目标函数

def objective_function(temp_step, G): s, alpha, beta = 0, 0.15, 4.0 for _, _, data in G.edges(data=True): x = data['flow_real'] + temp_step * data['descent'] s += data["FFT"] * (x + alpha * data["Capacity"] / (beta + 1) * (x / data["Capacity"]) ** (beta + 1)) return s

        该部分代码，对应本文1.4部分的目标函数，即：

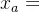
        如果需要求解系统最优模型，则目标函数为

        代码则需替换为：

def objective_function(temp_step, G): s, alpha, beta = 0, 0.15, 4.0 for _, _, data in G.edges(data=True): x = data['flow_real'] + temp_step * data['descent'] s += x * BPR(data["FFT"], x, data["Capacity"]) return s

3.9 一维搜索最优步长，并更新流量

def update_flow_real(G): # 这个函数用于调整流量，即flow_real，并更新weight best_step = get_best_step(G) # 获取最优步长 for _, _, data in G.edges(data=True): # 调整流量，更新路阻 data['flow_real'] += best_step * data["descent"] data['weight'] = BPR(data['FFT'], data['flow_real'], data['Capacity'])def get_best_step(G, tolerance=1e-4): result = minimize_scalar(objective_function, args=(G,), bounds=(0, 1), method='bounded', tol=tolerance) return result.x

3.10 主函数

def main(): G = build_network("Link.csv", "Node.csv") # 构建路网 draw_network(G) # 绘制交通路网图 od_df = pd.read_csv("ODPairs.csv") # 获取OD需求情况 all_none_initialize(G, od_df) # 初始化路网流量 print("初始化流量", list(nx.get_edge_attributes(G, 'flow_real').values())) epoch = 0 # 记录迭代次数 err, max_err = 1, 1e-4 # 分别代表初始值、最大容许误差 f_list_old = np.array(list(nx.get_edge_attributes(G, 'flow_real').values())) while err > max_err: epoch += 1 all_none_temp(G, od_df) # 全有全无分配，得到flow_temp get_descent(G) # 计算梯度，即flow_temp-flow_real update_flow_real(G) # 先是一维搜索获取最优步长，再调整流量，更新路阻 # 计算并更新误差err f_list_new = np.array(list(nx.get_edge_attributes(G, 'flow_real').values())) # 这个变量是新的路网流量列表 d = np.sum((f_list_new - f_list_old) ** 2) err = np.sqrt(d) / np.sum(f_list_old) f_list_old = f_list_new print("均衡流量", list(nx.get_edge_attributes(G, 'flow_real').values())) print("迭代次数", epoch) # 导出网络均衡流量 df = nx.to_pandas_edgelist(G) df = df[["source", "target", "flow_real"]].sort_values(by=["source", "target"]) df.to_csv("网络均衡结果.csv", index=False)if __name__ == '__main__': main() epoch，表示迭代次数err，表示误差初始值max_err，表示最大容许误差 f_list_new, f_list_old分别表示

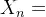
和

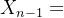
，用于计算误差

四、所用文件

        下载链接：交通分配