🐧主页详情：Choice~的个人主页

文章目录

搜索旋转排序数组方法一 二分查询最大最小值思路详解代码方法二 二分查询中间数 在排序数组中查找元素的第一个和最后一个位置、数组中的第K个最大元素和颜色分类在排序数组中查找元素的第一个和最后一个位置方法一 二分查找 数组中的第K个最大元素方法一方法二方法三题外话 颜色分类方法一 直接计算方法二 双指针遍历方法三 使用各种排序法

搜索旋转排序数组

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

你可以假设数组中不存在重复的元素。

你的算法时间复杂度必须是 O(log n) 级别。

示例 1:

输入: nums = [4,5,6,7,0,1,2], target = 0输出: 4

示例 2:

输入: nums = [4,5,6,7,0,1,2], target = 3输出: -1

方法一 二分查询最大最小值

思路

先算出 数组中最大最小值，利用 indexOf 计算之后要旋转位置，然后二分计算目标 target 位置

详解

计算数组中的最大最小值定义变量，数组长度等目标值大于数组最后一位时，数组查询位置从 0 到数字中在最大位置目标值小于等于数组最后一位时，数组查询位置从数组中最小值的位置开始，到数组的最后一位，3.4 两部为了定位数组查询区间循环二分查询，计算定位数组的中间值，数组的值等于目标查询结束不等于的情况，如果目标大于中间值，则定位数组最小值等于中间值+1，目标小于中间值，则定位数组中最大值等于中间值-1，继续循环查询即可，知道定位数组查询完毕，没有结果的话，返回 -1 代表不存在

代码

const search = function (nums, target) { const min = Math.min.apply(null, nums); const max = Math.max.apply(null, nums); const len = nums.length; let pos; let lo; let hi; let mid; if (target > nums[len - 1]) { pos = nums.indexOf(max); lo = 0; hi = pos; } else { pos = nums.indexOf(min); lo = pos; hi = len - 1; } while (lo <= hi) { mid = Math.ceil((lo + hi) / 2); if (nums[mid] === target) return mid; if (nums[mid] < target) { lo = mid + 1; } else { hi = mid - 1; } } return -1;};

复杂度分析：

时间复杂度：O(log(n))O(log(n))

过程会最多遍历一遍数组

空间复杂度：O(1)O(1)

只产生一次临时变量存储

方法二 二分查询中间数

思路

根据数组的中间数和左右节点的大小对比，来确定升序部分的位置，然后用二分法查询目标节点在数组中的位置

详解

计算数组长度，数组为0 直接返回-1定义左右值分别为数组第一个和最后一个的下标中间下标值为最大最小值的平均数如果数组中间数等于目标直接返回下标数组的中间值小于数组最后一个值，后半部分还处于升序，如果目标值在这部分数组中，则左下标等于中间值+1，代表目标值在后半部分数组，反着重新定义右下标为中间值-1，目标在前半数组数组中间值大于数组最后一个值，代表前半部分数组处于升序，如果目标在前半数组中，右标更新为中间值-1，反之，左下标更新为中间值+1二分查询到最后没找到目标值，则返回 -1 代表不存在

代码

const search = function(nums, target) { if(nums.length === 0){ return -1; } let left = 0; let right = nums.length - 1; let mid; while(left <= right){ mid = parseInt((left + right) / 2); if(nums[mid] === target){ return mid; } else if(nums[mid] < nums[right]) { if(nums[mid] < target && target <= nums[right]) { left = mid + 1; } else { right = mid - 1; } } else { if(nums[left] <= target && target < nums[mid]){ right = mid - 1; } else { left = mid + 1; } } } return -1;};

复杂度分析

时间复杂度：O(log(n))O(log(n))

过程会最多遍历一遍数组

空间复杂度：O(1)O(1)

只产生一次临时变量存储

在排序数组中查找元素的第一个和最后一个位置、数组中的第K个最大元素和颜色分类

在排序数组中查找元素的第一个和最后一个位置

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

你的算法时间复杂度必须是 O(log n) 级别。

如果数组中不存在目标值，返回 [-1, -1]。

示例

输入: nums = [5,7,7,8,8,10], target = 8输出: [3,4]输入: nums = [5,7,7,8,8,10], target = 6输出: [-1,-1]

方法一 二分查找

思路

由于数组已经时升序排列，可直接根据二分查找，往左定位第一个位置，往右定位最后一个位置 二分查找的实现上可以使用循环或者递归。

详解

根据二分查找，找到左边第一个不小于目标值的位置从上一步中的位置开始到最后，二分查找，确定右边最后一个符合条件值的位置得到结果

function getBinarySearchLowerBound (array, low, high, target) { // 找到第一个不小于目标值的位置 while (low < high) { const mid = Math.floor((low + high) / 2); if (array[mid] < target) { low = mid + 1; } else { high = mid; } } // 如果相等，则匹配，否则不匹配 return array[low] === target ? low : -1;}function getBinarySearchUpperBound (array, low, high, target) { // 找到第一个不大于目标值的位置 while (low < high) { const mid = Math.ceil((low + high) / 2); if (array[mid] > target) { high = mid - 1; } else { low = mid; } } // 如果相等，则匹配，否则不匹配 return array[high] === target ? high : -1;}const searchRange = function (nums, target) { const size = nums.length; const low = getBinarySearchLowerBound(nums, 0, size - 1, target); if (low === -1) { return [-1, -1]; } // 从左边数字的位置开始 const high = getBinarySearchUpperBound(nums, low >= 0 ? low : 0, size - 1, target); return [low, high];};

复杂度分析

时间复杂度：O(log(n))O(log(n))

过程中最差情况会遍历二遍数组

空间复杂度：O(1)O(1)

产生三个临时变量存储

数组中的第K个最大元素

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例1：

输入: [3,2,1,5,6,4] 和 k = 2输出: 5

示例2：

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4输出: 4

说明：你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

方法一

思路

首先通过快速排序的方法将数组升序排序，此时数组的头部为最小的元素，尾部为数组最大的元素。题目要求找到数组中的第 K 个最大的元素，即返回 length - k 个元素即可。

详解

本方法采用快速排序法；首先通过 arr[Math.floor((start + end) / 2)] 找到数组中间的元素作为主元；然后使用双指针，分别从数组的头部和尾部遍历数组；遍历过程中，把比主元小的数都放到主元的左边，比主元大的数都放到主元的右边，实现数组的升序排序；返回第 length - k 个元素，即为数组中第 k 个最大的元素。

1

const findKthLargest = function (nums, k) { return findK(nums, 0, nums.length - 1, nums.length - k);};function findK (arr, start, end, k) { if (start === end) return arr[start]; // 主元 const pivot = arr[Math.floor((start + end) / 2)]; let i = start; let j = end; while (i <= j) { while (arr[i] < pivot) i++; while (arr[j] > pivot) j--; if (i <= j) { swap(arr, i, j); i++; j--; } } // 二分查到k位置 if (k >= (i - start)) { return findK(arr, i, end, k - i + start); } else { return findK(arr, start, i - 1, k); }}// 元素交换function swap (arr, i, j) { const temp = arr[i]; arr[i] = arr[j]; arr[j] = temp;}

复杂度分析

时间复杂度： O(n log n)O(nlogn)

上述解法中，采用了快速排序的方法，快排的时间复杂度 O(n log n)O(nlogn)。

空间复杂度： O(1)O(1)

上述解法中，申请了四个额外的临时存储空间，这将耗费 O(1)O(1) 的空间。

方法二

思路

首先通过最小堆排序的方法将数组升序排序，排序完的数组如下图所示：

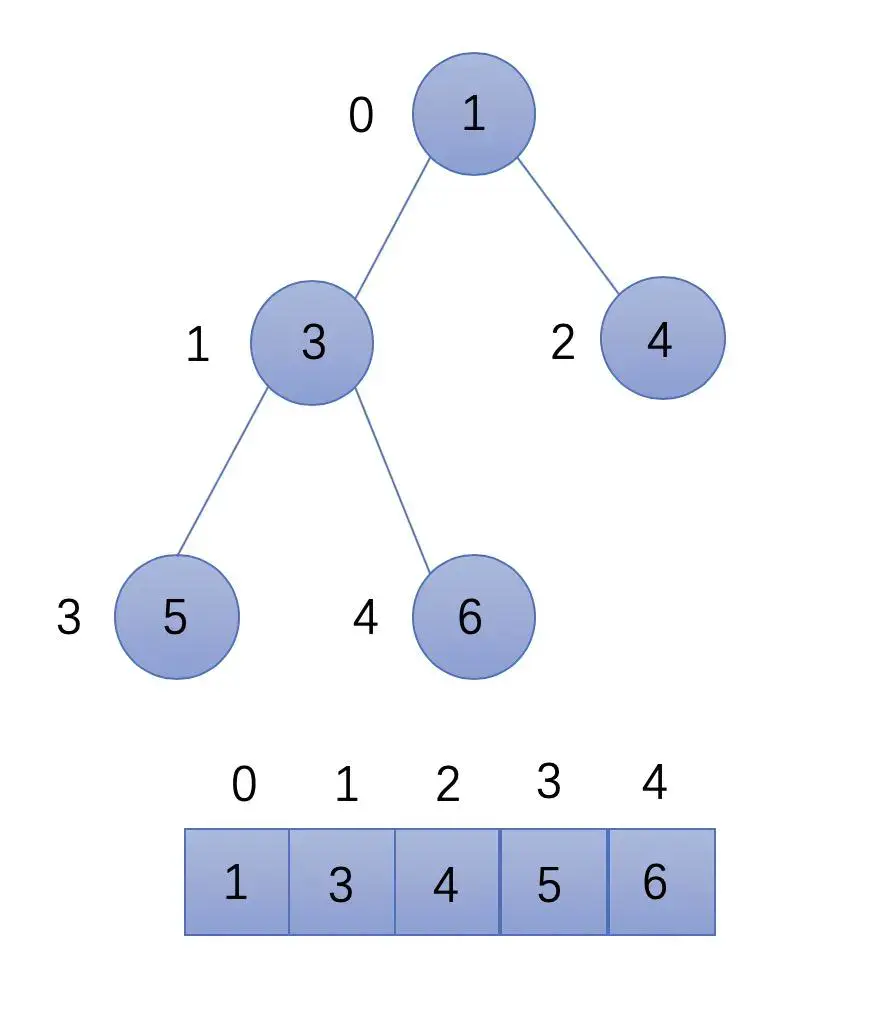
此时数组的头部为最小的元素，尾部为数组最大的元素。题目要求找到数组中的第 K 个最大的元素，即返回 length - k 个元素即可。

详解

本方法采用最小堆排序法；首先建立最小堆，将每个叶子结点视为一个堆，再将每个叶子结点与其父节点一起构成一个包含更多结点的堆；所以在构造堆的时候，首先需要找到最后一个结点的父节点，从这个节点开始构造最小堆，直到该节点前面的所有分支节点都处理完毕；然后返回第 length - k 个，即为数组中第 k 个最大的元素。

const findKthLargest = function (nums, k) { const size = nums.length; // 建立堆 for (let i = parseInt(size / 2) + 1; i >= 0; i--) { heapify(nums, i, size); } // 排序 for (let j = size - 1; j >= size - k; j--) { // 得到本次的最大，将最大的与最后一个交换位子 swap(nums, 0, j); heapify(nums, 0, j); } return nums[size - k];};function heapify (arr, x, length) { // 左右两个子节点 const l = 2 * x + 1; const r = 2 * x + 2; let largest = x; if (l < length && arr[l] > arr[largest]) { largest = l; } if (r < length && arr[r] > arr[largest]) { largest = r; } if (largest !== x) { swap(arr, x, largest); // 递归交换以下的是否也建好堆. heapify(arr, largest, length); }}function swap (arr, i, j) { const temp = arr[i]; arr[i] = arr[j]; arr[j] = temp;}

复杂度分析

时间复杂度： O(n log n)O(nlogn)

上述解法中，采用了堆排序的方法，堆排序的时间复杂度 O(n log n)O(nlogn)。

空间复杂度： O(1)O(1)

上述解法中，申请了四个额外的临时存储空间，这将耗费 O(1)O(1) 的空间。

方法三

思路

首先通过冒泡排序的方法将数组升序排序，此时数组的头部为最小的元素，尾部为数组最大的元素。题目要求找到数组中的第 K 个最大的元素，即返回 length - k 个元素即可。

详解

本方法采用经典冒泡排序法；比较相邻的元素，如果第一个比第二个大，就交换他们两个；对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对；完成步骤 3 后，最后的元素会是最大的数，实现升序排序；返回第 len-k 个元素，即为数组中第 k 个最大的元素。

const findKthLargest = function (nums, k) { const len = nums.length; for (let i = len - 1; i > 0; i--) { // 冒泡排序 for (let j = 1; j <= i; j++) { // 异或交换，详见题外话解析 if (nums[j - 1] > nums[j]) { nums[j - 1] ^= nums[j]; nums[j] ^= nums[j - 1]; nums[j - 1] ^= nums[j]; } } if (i === (len - k)) { return nums[i]; } } return nums[0];};

复杂度分析

时间复杂度： O(n^2)O(n2)

上述解法中，内外两层循环，时间复杂度 O(n^2)O(n2)。

空间复杂度： O(1)O(1)

上述解法中，最优的情况是开始时元素已经按顺序排好，空间复杂度为 0 ，最差的情况是开始时元素逆序排序，此时空间复杂度 O(n)O(n)，平均空间复杂度 O(1)O(1)。

复杂度分析：

时间复杂度： O(n^2)O(n2)，内外两层循环，时间复杂度 O(n^2)O(n2)空间复杂度： O(1)O(1)，最优的情况是开始时元素已经按顺序排好，空间复杂度为0，最差的情况是开始时元素逆序排序，此时空间复杂度 O(n)O(n)，平均空间复杂度 O(1)O(1)

题外话

对于给定两个整数a,b，下面的异或运算可以实现a,b的交换，而无需借助第3个临时变量：

a = a ^ b;b = a ^ b;a = a ^ b;

这个交换两个变量而无需借助第3个临时变量过程，其实现主要是基于异或运算的如下性质：

任意一个变量X与其自身进行异或运算，结果为0，即X ^ X=0任意一个变量X与0进行异或运算，结果不变，即X ^ 0=X异或运算具有可结合性，即a ^ b ^ c =（a ^ b）^ c= a ^（ b ^ c）异或运算具有可交换性，即a ^ b = b ^ a

分析：

第一步： a = a ^ b;

完成后 a变量的结果为a ^ b

第二步： b = a ^ b;

此时赋值号右边的 a 保存的是 a ^ b 的值，那么将赋值号右边的 a 用 a ^ b 替换，

得到（a ^ b） ^ b = a ^ (b ^ b)=a ^ 0=a,

即经过第二步运算后 b 中的值为 a ，即 b=a ，将 a 换到了 b 里

第三步： a = a ^ b;

此时赋值号右边的 a 保存的仍然是 a ^ b 的值，不变，而赋值号右边的 b 已经是 a 了，

将赋值号右边的 a,b 分别进行替换，

即此时赋值号右边 a ^ b=（a ^ b）^ a=a ^ b^ a=a ^ a^ b=0^ b=b, 该值赋值给 a ,即 a=b

即经过第三步运算后 a 中的值为 b ，即 a=b, 将 b 换到了 a 里

这样经过如上的三步骤，完成了交换两个变量 a,b 而无需借助第 3 个临时变量过程。

颜色分类

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

注意: 不能使用代码库中的排序函数来解决这道题。

示例

输入: [2,0,2,1,1,0]输出: [0,0,1,1,2,2]

方法一 直接计算

思路

直接遍历整个数组，分别计算出红蓝白球的个数，然后按照红色、白色、蓝色顺序依次存入数组。

详解

设定三个变量 red, white，blue 分别表示红球、白球和蓝球。遍历数组，遇到 0 则使 red 自增1，遇到 1 则使 white 自增1，遇到 2 则使 blue 自增1。根据红白蓝的个数，依次将 0，1，2 存入数组。

/** * @param {number[]} nums * @return {void} Do not return anything, modify nums in-place instead. */const sortColors = function (nums) { let red = 0; let blue = 0; let white = 0; for (let i = 0; i < nums.length; i++) { if (nums[i] === 0) { red++; } else if (nums[i] === 1) { blue++; } else if (nums[i] === 2) { white++; } } let index = 0; for (let i = 0; i < red; i++) { nums[index++] = 0; } for (let i = 0; i < blue; i++) { nums[index++] = 1; } for (let i = 0; i < white; i++) { nums[index++] = 2; }};

复杂度分析

时间复杂度： O(n)O(n)空间复杂度： O(n)O(n)

方法二 双指针遍历

思路

设定三个指针 begin, end, i，用 i 遍历数组，遇到 0，1 时分别将值与 begin, end 指向的值交换。这种方法相对于方法一的好处是只使用了一个常数空间。

详解

设定一头一尾两个指针 begin 和 end，然后用一个指针 i 从头开始遍历数组。如果遇到 0，则将该数值与begin指向的值交换，并且使begin向后移一位。如果遇到 2，则将该数值与end指向的值交换，并且使end向前移一位，并且此时不需自加 i。如果遇到 1，则继续。最终得到新数组。

/** * @param {number[]} nums * @return {void} Do not return anything, modify nums in-place instead. */const sortColors = function (nums) { let begin = 0; let end = nums.length - 1; let i = 0; while (i <= end) { if (nums[i] === 0) { nums[i] = nums[begin]; nums[begin] = 0; i++; begin++; } else if (nums[i] === 2) { nums[i] = nums[end]; nums[end] = 2; end--; } else { i++; } }};

复杂度分析

时间复杂度：O(n)O(n)空间复杂度：O(1)O(1)

方法三 使用各种排序法

思路

本题的实质是将数字从小到大排序，可以使用各种排序法（冒泡排序法，选择排序法，快速排序法等），这里举一个冒泡排序法的例子。

1

/** * @param {number[]} nums * @return {void} Do not return anything, modify nums in-place instead. */const sortColors = function (nums) { for (let i = 0; i < nums.length; i++) { for (let j = 0; j < nums.length - i; j++) { if (nums[j] > nums[j + 1]) { const tem = nums[j]; nums[j] = nums[j + 1]; nums[j + 1] = tem; } } }};

复杂度分析

时间复杂度：O(n^2)O(n2)

遍历了两次含n个元素的空间

空间复杂度：O(1)O(1)

排序过程没有用到新的空间存储数据