一、限幅滤波法

1、方法：

根据经验判断两次采样允许的最大偏差值（设为A）

每次检测到新值时判断：

a. 如果本次值与上次值之差<=A，则本次值有效

b. 如果本次值与上次值之差>A，则本次值无效，放弃本次值，用上次值代替本次值

2、优点：

能有效克服因偶然因素引起的脉冲干扰

3、缺点

无法抑制那种周期性的干扰

平滑度差

<code>/* A值根据实际调，Value有效值，new_Value当前采样值，程序返回有效的实际值 */

#define A 10

char Value;

char filter()

{

    char new_Value;

    new_Value = get_ad(); // 获取采样值

    if( abs(new_Value - Value) > A)   

        return Value;     // abs()取绝对值函数

    return new_Value;

}

二、中位值滤波法

1、方法：

连续采样N次（N取奇数），把N次采样值按大小排列

取中间值为本次有效值

2、优点：

能有效克服因偶然因素引起的波动干扰

对温度、液位的变化缓慢的被测参数有良好的滤波效果

3、缺点：

对流量、速度等快速变化的参数不宜

#define N 11

char filter()

{

    char value_buf[N];

    char count, i, j, temp;

    for(count = 0; count < N; count ++) //获取采样值

    {

        value_buf[count] = get_ad();

        delay();

    }

    for(j = 0; j < (N-1); j++)

    {

        for(i = 0; i < (n-j); i++)

        {

            if(value_buf[i] > value_buf[i+1])

            {

                temp = value_buf[i];

                value_buf[i] = value_buf[i+1];

                value_buf[i+1] = temp;

            }

        }

    }

    return value_buf[(N-1)/2];

}

三、算术平均滤波法

1、方法：

连续取N个采样值进行算术平均运算

N值较大时：信号平滑度较高，但灵敏度较低

N值较小时：信号平滑度较低，但灵敏度较高

N值的选取：一般流量，N=12；压力：N=4

2、优点：

适用于对一般具有随机干扰的信号进行滤波

这样信号的特点是有一个平均值，信号在某一数值范围附近上下波动

3、缺点：

对于测量速度较慢或要求数据计算速度较快的实时控制不适用

比较浪费RAM

#define N 12

char filter()

{

    int sum = 0;

    for(count = 0; count < N; count++)

    {

        sum += get_ad(count);

    } 

    return (char)(sum/N);

}

四、递推平均滤波法

1、方法：

把连续取N个采样值看成一个队列

队列的长度固定为N

每次采样到一个新数据放入队尾，并扔掉原来队首的一次数据.(先进先出原则)

把队列中的N个数据进行算术平均运算，就可获得新的滤波结果

N值的选取：流量，N=12；压力：N=4；液面，N=4 ~ 12；温度，N=1 ~ 4

2、优点：

对周期性干扰有良好的抑制作用，平滑度高

适用于高频振荡的系统

3、缺点：

灵敏度低

对偶然出现的脉冲性干扰的抑制作用较差

不易消除由于脉冲干扰所引起的采样值偏差

不适用于脉冲干扰比较严重的场合

比较浪费RAM

#define N 10

u16 value_buf[N];

u16 sum=0;

u16 curNum=0;

u16 moveAverageFilter()

{

    if(curNum < N)

    {

        value_buf[curNum] = getValue();

        sum += value_buf[curNum];

        curNum++;

        return sum/curNum;

    }

    else

    {

        sum -= sum/N;

        sum += getValue();

        return sum/N;

    }

}

五、中位值平均滤波法

1、方法：

相当于“中位值滤波法”+“算术平均滤波法”

连续采样N个数据，去掉一个最大值和一个最小值

然后计算N-2个数据的算术平均值

N值的选取：3~14

2、优点：

融合了两种滤波法的优点

对于偶然出现的脉冲性干扰，可消除由于脉冲干扰所引起的采样值偏差

3、缺点：

测量速度较慢，和算术平均滤波法一样

比较浪费RAM

char filter()

{

    char count, i, j;

    char Value_buf[N];

    int sum = 0;

    for(count = 0; count < N; count++)

    {

        Value_buf[count] = get_ad();

    } 

    for(j = 0; j < (N-1); j++)

    {

        for(i = 0; i < (N-j); i++)

        {

            if(Value_buf[i] > Value_buf[i+1])

            {

                temp = Value_buf[i];

                Value_buf[i] = Value_buf[i+1];

                Value_buf[i+1] = temp;

            }

        }  

    }    

    for(count = 1; count < N-1; count ++)

    {

        sum += Value_buf[count];

    }

    return (char)(sum/(N-2));

}

六、限幅平均滤波法

1、方法：

相当于“限幅滤波法”+“递推平均滤波法”

每次采样到的新数据先进行限幅处理，

再送入队列进行递推平均滤波处理

2、优点：

融合了两种滤波法的优点

对于偶然出现的脉冲性干扰，可消除由于脉冲干扰所引起的采样值偏差

3、缺点：

比较浪费RAM

#define A 10

#define N 12

char value, i = 0;

char value_buf[N];

char filter()

{

    char new_value, sum = 0;

    new_value = get_ad();

    if(Abs(new_value - value) < A)  

        value_buf[i++] = new_value;

    if(i==N)  

        i=0;

    for(count = 0; count < N; count++)

    {

        sum += value_buf[count];

    }

    return (char)(sum/N);

}

七、一阶滞后（低通）滤波法

1、方法：

取a=0~1

本次滤波结果=（1-a）本次采样值+a上次滤波结果

2、优点：

对周期性干扰具有良好的抑制作用

适用于波动频率较高的场合

3、缺点：

相位滞后，灵敏度低

滞后程度取决于a值大小

不能消除滤波频率高于采样频率的1/2的干扰信号

/*为加快程序处理速度，取a=0~100*/

#define a 30

char value;

char filter()

{

    char new_value;

    new_value = get_ad();

    return ((100-a)*value + a*new_value);

}

八、加权递推平均滤波法

1、方法：

是对递推平均滤波法的改进，即不同时刻的数据加以不同的权

通常是，越接近现时刻的数据，权取得越大。

给予新采样值的权系数越大，则灵敏度越高，但信号平滑度越低

2、优点：

适用于有较大纯滞后时间常数的对象

和采样周期较短的系统

3、缺点：

对于纯滞后时间常数较小，采样周期较长，变化缓慢的信号

不能迅速反应交易系统当前所受干扰的严重程度，滤波效果差

/* coe数组为加权系数表 */

#define N 12

char code coe[N] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12};

char code sum_coe = (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12);

char filter()

{

    char count;

    char value_buf[N];

    int sum = 0;

    for(count = 0; count < N; count++)

    {

        value_buf[count] = get_ad();

    }

    for(count = 0; count < N; count++)

    {

        sum += value_buf[count] * coe[count];

    } 

    return (char)(sum/sum_coe);

}

九、消抖滤波法

1、方法：

设置一个滤波计数器

将每次采样值与当前有效值比较：

如果采样值＝当前有效值，则计数器清零

如果采样值>或<当前有效值，则计数器+1，并判断计数器是否>=上限N(溢出)

如果计数器溢出，则将本次值替换当前有效值，并清计数器

2、优点：

对于变化缓慢的被测参数有较好的滤波效果，

可避免在临界值附近控制器的反复开/关跳动或显示器上数值抖动

3、缺点：

对于快速变化的参数不宜

如果在计数器溢出的那一次采样到的值恰好是干扰值，则会将干扰值当作有效值导入交易系统

#define N 12

char filter()

{

    char count = 0, new_value;

    new_value = get_ad();

    while(value != new_value)

    {

        count++;

        if(count >= N) 

            return new_value;

        new_value = get_ad();

    }

    return value;

}

十、限幅消抖滤波法

1、方法：

相当于“限幅滤波法”+“消抖滤波法”

先限幅，后消抖

2、优点：

继承了“限幅”和“消抖”的优点

改进了“消抖滤波法”中的某些缺陷，避免将干扰值导入系统

3、缺点：

对于快速变化的参数不宜

#define A 10

#define N 12

char value;

char filter()

{

    char new_value, count = 0;

    new_value = get_ad();

    while(value != new_value)

    {

        if(Abs(value - new_value) < A)

        {

            count++;

            if(count >= N) 

                return new_value;

            new_value = get_ad();

        }

        return value;

    }

}

 附录：

1、FIR滤波

FIR有限长滤波器，有限长指的是滤波器的脉冲响应为有限长的序列

输入X经过滤波器H得到滤波后的输出Y

表达成差分方程形式就是：

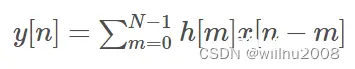
使用不同的窗函数会有不同的滤波性能（衰减程度和过渡带大小的不一样）

窗函数的介绍以及画出常见窗函数（汉宁窗，矩形窗，汉明窗，布莱克曼窗）的时域图和频谱图-CSDN博客

参考链接：https://blog.csdn.net/weixin_59250390/article/details/134329056

参考代码：

<code>#include <stdlib.h>

#include <math.h>

// FIR低通滤波器设计函数

void fir_lowpass(float *input, float *output, int N, float cutoff_freq, float sample_freq) {

int i, j;

float *b;

b = (float *)malloc((N + 1) * sizeof(float));

// 设计滤波器系数b[n]

float N_normalized = (N - 1) / 2.0;

for (i = 0; i < N + 1; i++) {

b[i] = (float)(sin(cutoff_freq * 2 * M_PI / sample_freq * (i - N_normalized)) / (i - N_normalized));

}

// 滤波器滤波

float acc = 0.0;

for (i = 0; i < N; i++) {

acc += input[i] * b[N - i];

}

output[0] = acc;

for (j = 1; j < N; j++) {

acc -= input[j - 1] * b[N + 1 - j];

acc += input[j + N - 1] * b[N - j];

output[j] = acc;

}

free(b);

}

int main() {

int N = 10; // 滤波器阶数

float cutoff_freq = 0.3; // 截止频率（0.3 * 采样频率）

float sample_freq = 1.0; // 采样频率

float input[N] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; // 输入数据

float output[N]; // 输出数据

fir_lowpass(input, output, N, cutoff_freq, sample_freq);

// 打印输出

for (int i = 0; i < N; i++) {

printf("%.2f ", output[i]);

}

return 0;

}

2、卡尔曼滤波

卡尔曼滤波算法是一种用于估计未知变量的状态的数学算法。它可以通过过滤传感器测量值，来估计出最可能的状态值。该算法最初是为航空航天应用而开发的，但现在已广泛应用于各种领域，如自动驾驶汽车、机器人、船舶控制等。卡尔曼滤波算法基于状态空间模型，其中包含系统的状态、测量值和控制输入。利用贝叶斯定理和高斯分布等概率统计学原理，卡尔曼滤波算法可以计算出最优状态估计值和协方差矩阵，从而实现对系统状态的精确估计和预测。

该算法具有高精度、快速收敛、自适应性强等优点，是一种非常有效的状态估计算法。

参考代码：

#include <stdio.h>

// 卡尔曼滤波器结构体

typedef struct {

float x; // 状态变量

float p; // 状态误差协方差矩阵

float q; // 过程噪声协方差

float r; // 测量噪声协方差

float h; // 测量矩阵

float k; // 卡尔曼增益

float y; // 测量值

} KalmanFilter;

// 卡尔曼滤波器更新函数

void kalmanFilterUpdate(KalmanFilter *kf, float measurement) {

kf->y = measurement - kf->h * kf->x; // 测量更新

kf->p = kf->h * kf->p * kf->h->transpose() + kf->r; // 预测误差更新

kf->k = kf->p * kf->h->transpose() / (kf->h * kf->p * kf->h->transpose() + 1.0f); // 卡尔曼增益计算

kf->x = kf->x + kf->k * kf->y; // 状态更新

kf->p = (1.0f - kf->k) * kf->p; // 预测误差新值

}

int main() {

KalmanFilter filter;

filter.x = 0.0f;

filter.p = 1.0f;

filter.q = 1e-5f;

filter.r = 1.0f;

filter.h = 1.0f;

float measurement = 1.0f; // 假设的测量值

kalmanFilterUpdate(&filter, measurement);

printf("状态变量: %f\n", filter.x);

printf("状态误差协方差矩阵: %f\n", filter.p);

return 0;

}