总结一下比较常用的一些数据滤波算法，一阶算法可以算是比较基础，通过基本的原理可以引出其他多阶算法或者组合算法

六种常用滤波算法 mcu平台c code

1. 中值滤波2. 滑动均值滤波3. rc-低通滤波4. rc-高通滤波5. rc-带通滤波6. 卡尔曼滤波

1. 中值滤波

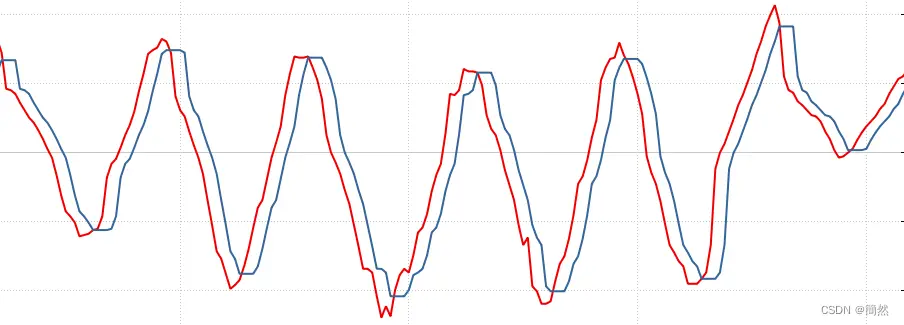
中值滤波顾名思义就是将连续的数据取其大小的中值代替，通常用在信号平滑且存在噪声突刺情况可以有效过滤异常数据，缺点是当信号噪声过密时滤波效果不明显，排序算法需要优化以减小ram与计算时间。

//头文件

#define MID_AVG_FILTER_SIZE (7U) //定义滤波窗口大小通常位奇数

typedef struct

{

float dataBuf[MID_AVG_FILTER_SIZE]; //采样数据区

u16 index; //实现循环队列的队尾下标

} mid_avg_filter_t;

float Mid_avg_filter(mid_avg_filter_t* const filter, const float data);

//源文件

/*******************************************************************************

* @fn Mid_avg_filter

* @brief 实现中值滤波

* @param filter 滤波器

* @param data 最新数据

* @return 滤波后的结果

******************************************************************************/

float Mid_avg_filter(mid_avg_filter_t * const filter, const float data)

{

float tem;

u16 i, j;

static mid_avg_filter_t f_tmp; //临时副本，用于排序

//采用循环队列形式将最新数据入队

filter->;dataBuf[filter->index] = data;

filter->index = (filter->index + 1) % MID_AVG_SIZE;

//采用冒泡法将滤波器内数据升序排序

f_tmp=*filter;

for (i = 0; i < MID_AVG_SIZE - 1; i ++) //MID_AVG_FILTER_SIZE-1不用与自己比较

{

u16 count = 0;

for (j = 0; j < MID_AVG_SIZE - 1 - i; j++)

{

if (f_tmp.dataBuf[j] > f_tmp.dataBuf[j + 1])

{

tem = f_tmp.dataBuf[j];

f_tmp.dataBuf[j] = f_tmp.dataBuf[j + 1];

f_tmp.dataBuf[j + 1] = tem;

count = 1;

}

}

if (count == 0)//如果某一趟没有交换位置，则说明已经排好序，直接退出循环

break;

}

//取中值

if(MID_AVG_SIZE%2==0)//判断奇偶

{

return (f_tmp.dataBuf[MID_AVG_SIZE/2]+f_tmp.dataBuf[(MID_AVG_SIZE/2)-1])/2;

}

return f_tmp.dataBuf[(MID_AVG_SIZE-1)/2];

}

//使用

mid_avg_filter_t filter={ 0};

float dataSrc; // 采样数据

float dataDest; //

//dataSrc=...//更新采样数据

dataDest=Mid_avg_filter(&mid_filter,dataSrc);//获取滤波数据

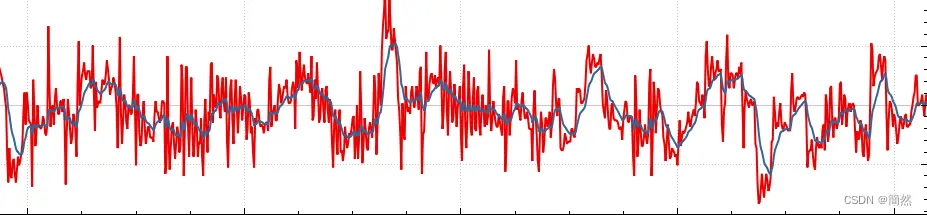
结果（红色为采样数据，蓝色为滤波数据）

2. 滑动均值滤波

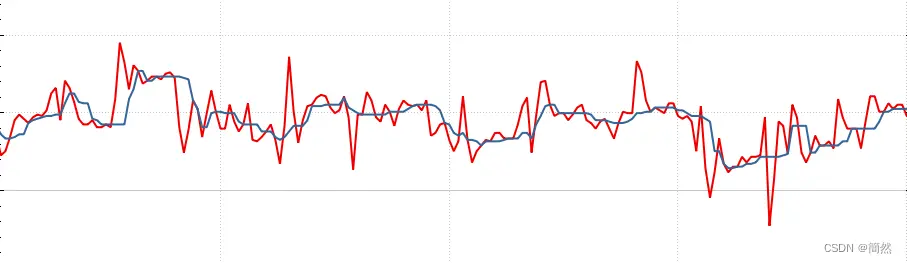
滑动均值滤波原理是在一组连续的采样数据中，按照某个数据块大小，连续对该块大小的数据取均值，看起来就像一个窗口划过这组数据。

优点；对于数据处理权重一致，能够将平均分布的噪声点处理综合掉。能够通过控制滑动窗口的大小控制平滑度。

缺点：窗口较大容易造成较大滞后性，且脉冲干扰抑制不明显。

<code>//头文件

#define SLID_WINDOW_SIZE (4U) //滑动窗口大小

typedef struct

{

float dataBuf[SLID_WINDOW_SIZE]; //采样数据区

u16 index; //实现循环队列的队尾下标

u16 size; //当前窗口内元素个数

} slid_avg_filter_t;

float Slid_avg_filter(slid_avg_filter_t* const filter, const float data);

//源文件

/*******************************************************************************

* @fn Slid_avg_filter

* @brief 实现滑动滤波

* @param filter 滤波器

* @param data 最新数据

* @return 滤波后的结果

******************************************************************************/

float Slid_avg_filter(slid_avg_filter_t* const filter, const float data)

{

double tem=0;

//采用循环队列形式将最新数据入队

filter->;dataBuf[filter->index] = data;

filter->index = (filter->index + 1) % SLID_WINDOW_SIZE;

if(filter->size<SLID_WINDOW_SIZE)filter->size+=1;

//取平均

for(u16 i=0;i<filter->size;i++)

{

tem+=filter->dataBuf[i];

}

tem/=filter->size;

return tem;

}

//使用

slid_avg_filter_t slid_filter={ 0};

float dataSrc; // 采样数据

float dataDest; //

//dataSrc=...//更新采样数据

dataDest=Slid_avg_filter(&slid_filter,idataSrc);//获取滤波数据

结果（红色为采样数据，蓝色为滤波数据）

3. rc-低通滤波

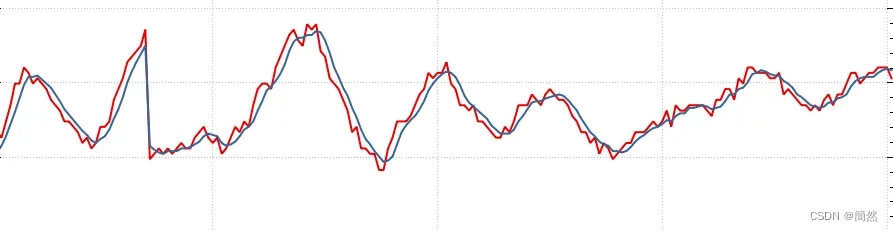
一阶低通滤波器（Low Pass Filter，LPF），核心参数为截止频率fc，该算法可以保留截止频率以内的信号，而衰减截止频率之外的信号。主要用于去除高频噪声。

一阶低通滤波公式如下：

y

n

=

a

x

n

+

(

1

−

a

)

y

n

−

1

等价于

:

y

n

=

y

n

−

1

+

a

(

x

n

−

y

n

−

1

)

其中

:

a

=

T

s

T

s

+

R

C

=

T

s

T

S

+

1

2

π

f

c

=

2

π

f

c

T

s

2

π

f

c

T

s

+

1

y_n=ax_n+(1-a)y_{n-1} \\等价于:\\ y_n=y_{n-1}+a(x_n-y_{n-1}) \\其中: \\ a= \frac {T_s} { {T_s+RC}}= {\frac {T_s}{T_S+\frac{1}{2 \pi f_c}}}=\frac{2\pi f_cT_s}{2\pi f_cT_s+1}

yn​=axn​+(1−a)yn−1​等价于:yn​=yn−1​+a(xn​−yn−1​)其中:a=Ts​+RCTs​​=TS​+2πfc​1​Ts​​=2πfc​Ts​+12πfc​Ts​​

参数说明：

y

n

y_n

yn​为本次滤波输出值，

y

n

−

1

y_{n-1}

yn−1​为上次滤波输出值，

x

n

x_n

xn​为本次采样值。

T

s

T_s

Ts​为采样周期（s），

f

c

f_c

fc​为截止频率(hz)。

a

a

a范围为[0,1]

<code>//头文件

#ifndef M_PI

#define M_PI (3.141592f)

#endif

typedef struct

{

float ts; //采样周期(s)

float fc; //截至频率(hz)

float lastYn; //上一次滤波值

float alpha; //滤波系数

} low_pass_filter_t;

//初始化滤波系数

void Init_lowPass_alpha(low_pass_filter_t* const filter,const float ts, const float fc);

//低通滤波

float Low_pass_filter(low_pass_filter_t* const filter, const float data);

//源文件

/*******************************************************************************

* @fn Init_lowPass_alpha

* @brief 初始化低通滤波器滤波系数

* @param filter 滤波器

* @param ts 采用周期 单位s

* @return fc 截至频率 单位hz

******************************************************************************/

void Init_lowPass_alpha(low_pass_filter_t* const filter,const float ts, const float fc)

{

float b=2*M_PI*fc*ts;

filter->;ts=ts;

filter->fc=fc;

filter->lastYn=0;

filter->alpha=b/(b+1);

}

/*******************************************************************************

* @fn Low_pass_filter

* @brief 低通滤波函数

* @param data 采样数据

* @return 滤波结果

******************************************************************************/

float Low_pass_filter(low_pass_filter_t* const filter, const float data)

{

float tem=filter->lastYn+(filter->alpha*(data-filter->lastYn));

filter->lastYn=tem;

return tem;

}

//使用

low_pass_filter_t low_pass_filter={ 0}; //定义滤波器

//初始化滤波器 采样周期0.005s 截至频率5hz

Init_lowPass_alpha(&low_pass_filter,0.005f,5);

...

float dataSrc; // 采样数据

float dataDest; //

//dataSrc=...//更新采样数据

dataDest=Low_pass_filter(&low_pass_filter,dataSrc);//获取滤波数据

结果（红色为采样数据，蓝色为滤波数据）

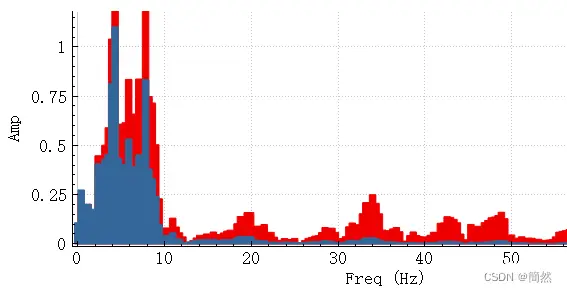
FFT分析如下，可以看到频率高于5hz 的数据被明显削弱

4. rc-高通滤波

高通滤波器可以滤除频率低于截止频率的信号，常用于处理存在累计漂移的数据中，例如陀螺仪角速度计

一阶高通滤波公式如下：

y

n

=

a

⋅

y

n

−

1

+

a

(

x

n

−

x

n

−

1

)

其中

:

a

=

R

C

R

C

+

T

s

=

1

2

π

f

c

1

2

π

f

c

+

T

s

=

1

1

+

2

π

f

c

T

s

y_n=a \cdot y_{n-1}+a(x_n-x_{n-1} ) \\其中: \\ a= \frac {RC} { {RC+T_s}}= {\frac{\frac{1}{2 \pi f_c}} {\frac{1}{2 \pi f_c}+T_s}}=\frac{1}{1+2\pi f_cT_s}

yn​=a⋅yn−1​+a(xn​−xn−1​)其中:a=RC+Ts​RC​=2πfc​1​+Ts​2πfc​1​​=1+2πfc​Ts​1​

参数说明：

y

n

y_n

yn​为本次滤波输出值，

y

n

−

1

y_{n-1}

yn−1​为上次滤波输出值，

x

n

x_n

xn​为本次采样值,

x

n

−

1

x_{n-1}

xn−1​为上次采样值，

T

s

T_s

Ts​为采样周期(s)，

f

c

f_c

fc​为下限频率（hz）。

a

a

a范围为[0,1]

<code>//头文件

typedef struct

{

float ts; //采样周期(s)

float fc; //下限频率(hz)

float lastYn; //上一次滤波值

float lastXn; //上一次采样值

float alpha; //滤波系数

} hight_pass_filter_t;

//初始化滤波系数

void Init_hightPass_alpha(hight_pass_filter_t* const filter,const float ts, const float fc);

//低通滤波

float Hight_pass_filter(hight_pass_filter_t* const filter, const float data);

//源文件

/*******************************************************************************

* @fn Init_hightPass_alpha

* @brief 初始高通滤波器滤波系数

* @param filter 滤波器

* @param ts 采用周期 单位s

* @return fc 截至频率 单位hz

******************************************************************************/

void Init_hightPass_alpha(hight_pass_filter_t* const filter,const float ts, const float fc)

{

float b=2*M_PI*fc*ts;

filter->;ts=ts;

filter->fc=fc;

filter->lastYn=0;

filter->lastXn=0;

filter->alpha=1/(1+b);

}

/*******************************************************************************

* @fn Hight_pass_filter

* @brief 高通滤波函数

* @param data 采样数据

* @return 滤波结果

******************************************************************************/

float Hight_pass_filter(hight_pass_filter_t* const filter, const float data)

{

float tem=((filter->alpha)*(filter->lastYn))+((filter->alpha)*(data-(filter->lastXn)));

filter->lastYn=tem;

filter->lastXn=data;

return tem;

}

//使用

hight_pass_filter_t hight_pass_filter={ 0}; //定义滤波器

//初始化滤波器 采样周期0.005s 下限频率20hz

Init_hightPass_alpha(&hight_pass_filter,0.005f,20);

...

float dataSrc; // 采样数据

float dataDest; //滤波数据

...

//这里生成一个合成的正弦波

Sin_Init(&sint1,0,3,0.5f,0.005f); //相移0，幅度3，频率0.5hz

Sin_Init(&sint2,0.5f*M_PI,1,1,0.005f);//相移0.5PI，幅度1，频率1hz

Sin_Init(&sint3,0,1,20,0.005f); //相移0，幅度1，频率20hz

//波形融合

dataSrc=Sin_cal(&sint1)+Sin_cal(&sint2)+Sin_cal(&sint3);

//dataSrc=...//更新采样数据

dataDest=Hight_pass_filter(&hight_pass_filter,dataSrc));//获取滤波数据

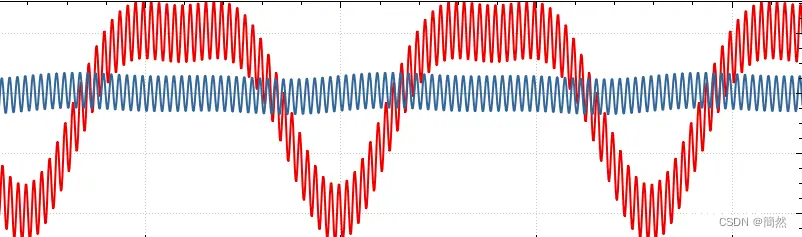
结果（红色为采样数据，蓝色为滤波数据）

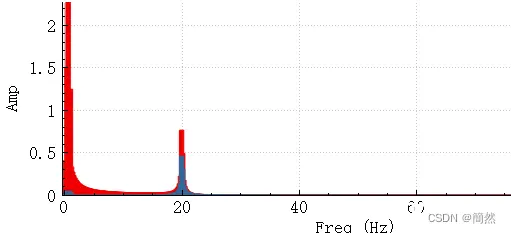
FFT分析如下，可以看到低频数据大部分被过滤掉

5. rc-带通滤波

由电路原理可以知道 带通滤波器可以由低通滤波和高通滤波器组成，将两部分串级可以形成带通滤波器。

如图生成三个正弦波

<code>Sin_Init(&sint1,0,0.5f,0.5f,0.005f); //相移0，幅度0.5，频率0.5hz

Sin_Init(&sint2,0,1,5,0.005f); //相移0，幅度1，频率5hz

Sin_Init(&sint3,0,0.5,50,0.005f); //相移0，幅度0.5，频率50hz

上图（红色：频率0.5hz 幅值0.5）（蓝色：频率5hz 幅值1）（黄色：频率50hz 幅值0.5）

合成波形如下

经过带通滤波频率在4hz-6hz 范围，结果为黑色波形

6. 卡尔曼滤波

当信号源中符合线性系统（齐次性和叠加性）并且噪声分布符合高斯分布时，可以使用卡尔曼对其滤波，具有较好效果。

卡尔曼本质是预测观测器，通过估计值与观测值得出最优值。关于观测卡尔曼滤波总结为5条公式,关于卡尔曼网上教程比较多，这里不做其他解释。

R和Q称为超调参数，两者会影响卡尔曼增益K，Q代表预测过程噪声，越小越好，R是测量噪声，当系统的观测噪声比较明显或者数据波动较大时，可以适当增加R的值（增大增益K）。当数据比较准确时，我们应该将R取小一点（减小增益K），Q取大一点。

<code>//头文件

typedef struct {

float X_last; //上一时刻的最优结果

float X_mid; //当前时刻的预测结果

float X_now; //当前时刻的最优结果

float P_mid; //当前时刻预测结果的协方差

float P_now; //当前时刻最优结果的协方差

float P_last; //上一时刻最优结果的协方差

float kg; //kalman增益

float A; //系统参数

float Q;

float R;

float H;

}kalman_filter_t;

///@codeEnd

//初始化卡尔曼滤波器

void Init_KalmanInfo(kalman_filter_t* const info, const float Q,const float R);

//卡尔曼过滤函数

float KalmanFilter(kalman_filter_t* const kalmanInfo, const float lastMeasurement);

//源文件

/************************************************

* @brief Init_KalmanInfo 初始化滤波器的初始值

* @param p 滤波器指针

* @param Q 预测噪声方差 由系统外部测定给定

* @param R 测量噪声方差 由系统外部测定给定

**************************************************/

void Init_KalmanInfo(kalman_filter_t* const p, const float Q,const float R)

{

//kalman* p = ( kalman*)malloc(sizeof( kalman));

p->;X_last = (float)0;

p->P_last = 1; //后验状态估计值误差的方差的初始值（不要为0问题不大）

p->Q = Q; //预测（过程）噪声方差 影响收敛速率，可以根据实际需求给出

p->R = R; //测量（观测）噪声方差 可以通过实验手段获得

p->A = 1; //标量卡尔曼

p->H = 1;

p->X_mid = p->X_last;

}

/************************************************

* @brief KalmanFilter 卡尔曼过滤函数

* @param p 滤波器指针

* @param lastMeasurement 当前最近值

* @return 过滤后的值

**************************************************/

float KalmanFilter(kalman_filter_t* const p, const float lastMeasurement)

{

p->X_mid =p->A*p->X_last; //x(k|k-1) = AX(k-1|k-1)+BU(k)

p->P_mid = p->A*p->P_last+p->Q; //p(k|k-1) = Ap(k-1|k-1)A'+Q

p->kg = p->P_mid/(p->P_mid+p->R); //kg(k) = p(k|k-1)H'/(Hp(k|k-1)'+R)

p->X_now = p->X_mid+p->kg*(lastMeasurement-p->X_mid); //x(k|k) = X(k|k-1)+kg(k)(Z(k)-HX(k|k-1))

p->P_now = (1-p->kg)*p->P_mid; //p(k|k) = (I-kg(k)H)P(k|k-1)

p->P_last = p->P_now; //状态更新

p->X_last = p->X_now;

return p->X_now;

}

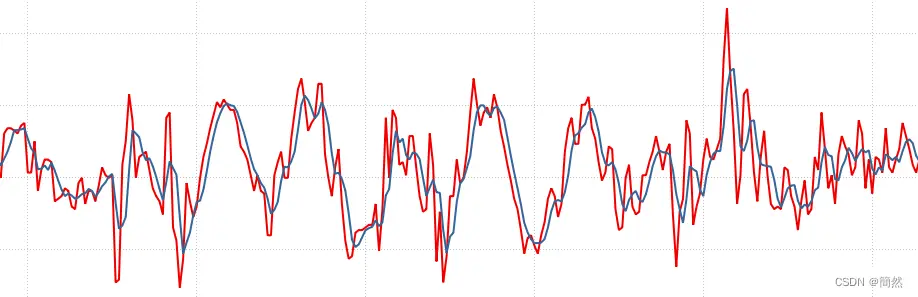
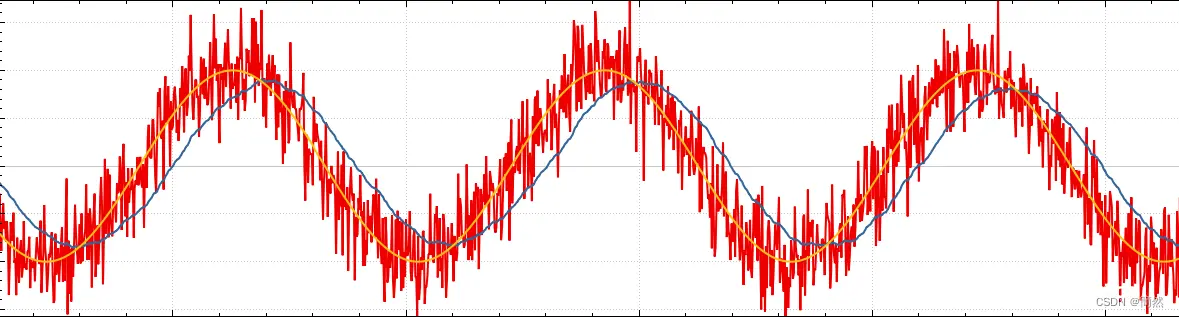
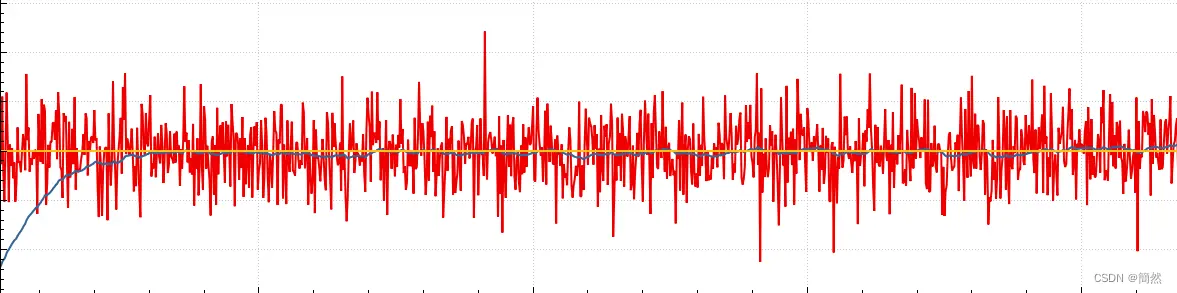
滤波效果图下如下，黄色线为原始数据线，红色为添加了高斯噪声的数据线（均值为1，方差为2.25），蓝色为滤波后的数据线，在滤波参数调节较大时，滞后性比较明显。