本文详细介绍常见的半监督学习算法及其实现，包括图形半监督学习、自训练、一致性正则化和生成对抗网络（GANs），并通过代码实战展示其具体应用。

关注TechLead，复旦AI博士，分享AI领域全维度知识与研究。拥有10+年AI领域研究经验、复旦机器人智能实验室成员，国家级大学生赛事评审专家，发表多篇SCI核心期刊学术论文，上亿营收AI产品研发负责人。

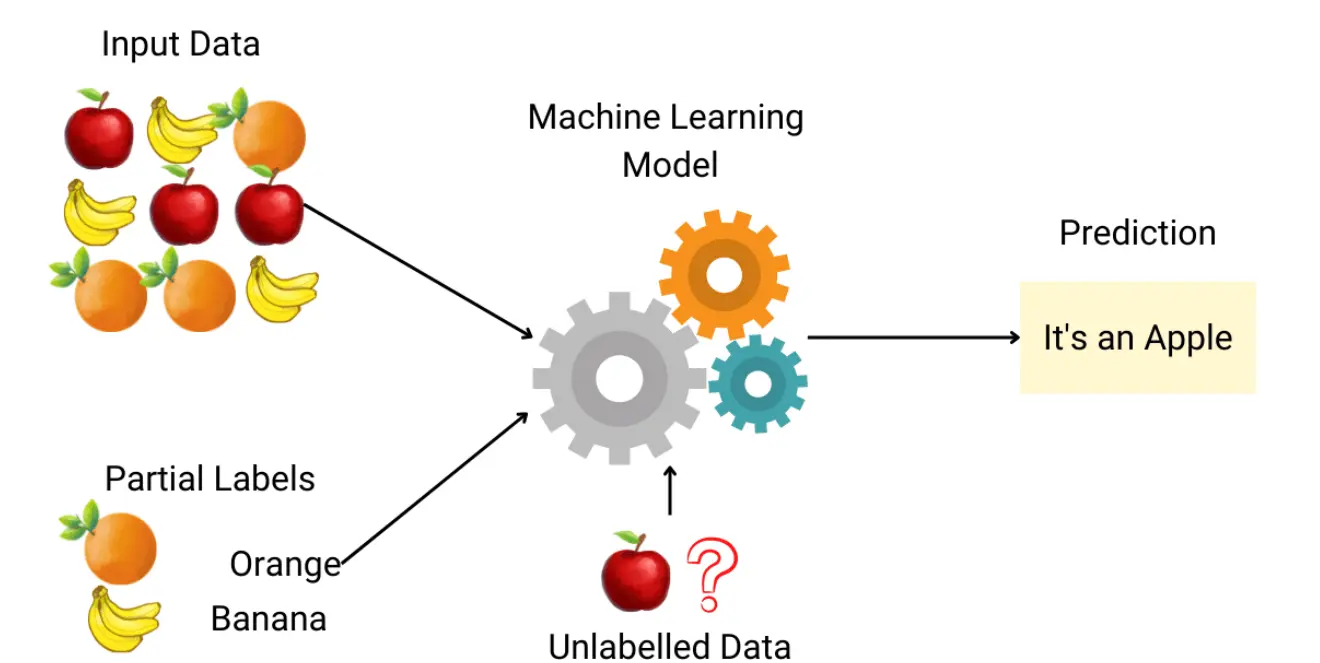
一、半监督学习概念

引言

在机器学习领域，数据是驱动模型训练的核心资源。然而，获取大量带标签的数据往往是昂贵且耗时的过程。半监督学习（Semi-Supervised Learning, SSL）通过利用大量未标记的数据和少量标记的数据，有效地缓解了这一问题。SSL不仅能够减少对标记数据的依赖，还能够在许多实际应用中提升模型的性能。

监督学习与无监督学习的比较

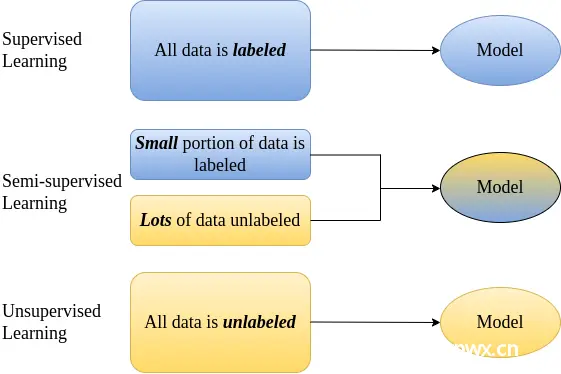
监督学习（Supervised Learning）依赖于大量带标签的数据来训练模型。这种方法的优势在于其明确的目标和易于评估的性能。然而，获取大规模标记数据集的成本高昂。

无监督学习（Unsupervised Learning）不依赖于带标签的数据，而是试图通过数据的内部结构和分布来学习模式。无监督学习的典型应用包括聚类和降维，但其缺点是难以直接评估和解释结果。

半监督学习位于监督学习和无监督学习之间，通过结合少量标记数据和大量未标记数据来构建模型。其目标是充分利用未标记数据的信息，提升模型的泛化能力。

半监督学习的定义和基本框架

定义：半监督学习是一种学习范式，旨在通过使用大量未标记数据和少量标记数据来训练模型。在许多实际应用中，获取未标记数据相对容易，而标记数据则相对稀缺且昂贵。SSL正是利用这种数据不平衡来提高学习效率和模型性能。

基本框架：半监督学习通常包括以下几个关键步骤：

数据准备：将数据集划分为标记数据和未标记数据。标记数据通常用于监督训练，而未标记数据用于引导模型的学习过程。

模型训练：通过联合使用标记数据和未标记数据进行模型训练。常见的方法包括自训练、图形半监督学习、一致性正则化和生成对抗网络等。

模型评估：使用独立的验证集或交叉验证来评估模型性能，确保模型能够有效利用未标记数据提升性能。

半监督学习的优势

减少标记需求：SSL能够有效减少对大规模标记数据的需求，降低数据获取的成本和时间。

提升模型性能：通过利用大量未标记数据，SSL可以捕捉到更多的数据分布信息，提升模型的泛化能力和鲁棒性。

应用广泛：SSL在许多实际场景中具有广泛的应用，包括图像分类、自然语言处理、语音识别等领域。

半监督学习的挑战

尽管半监督学习具有显著的优势，但在实际应用中仍然面临一些挑战：

模型复杂性：结合标记和未标记数据的训练过程可能导致模型复杂性增加，要求更高的计算资源和优化策略。

数据质量：未标记数据的质量和分布对于SSL的效果至关重要。低质量或噪声数据可能会对模型产生负面影响。

算法设计：设计有效的SSL算法需要在利用未标记数据和避免过拟合之间找到平衡，这对算法的设计和实现提出了更高的要求。

二、常见的半监督学习算法

半监督学习（Semi-Supervised Learning, SSL）通过利用大量未标记数据和少量标记数据，有效地提升了模型的性能和泛化能力。以下是一些常见且重要的半监督学习算法，每种方法在实际应用中都有其独特的优势和适用场景。

图形半监督学习（Graph-Based Semi-Supervised Learning）

图形半监督学习通过构建数据点之间的图结构，利用图上的连接关系来传播标签信息。其核心思想是相似的数据点在图结构中通常会有较强的连接，因此可以通过未标记数据点与标记数据点的连接关系来推断未标记数据点的标签。

典型方法

图正则化（Graph Regularization）：通过在监督学习的目标函数中添加图正则项，使得相邻数据点的标签更趋于一致。例如，拉普拉斯正则化（Laplacian Regularization）是常用的图正则化方法之一。

图嵌入（Graph Embedding）：将数据点嵌入到低维空间中，使得相似的数据点在低维空间中的距离较近。例如，拉普拉斯特征映射（Laplacian Eigenmaps）和局部线性嵌入（Locally Linear Embedding, LLE）等方法。

自训练（Self-Training）

自训练是一种简单而有效的半监督学习方法。它通过迭代的方式，逐步将高置信度的未标记数据加入到标记数据集中，重新训练模型，从而逐步提升模型性能。

步骤

初始训练：使用初始的标记数据训练一个基础模型。标签预测：使用训练好的模型对未标记数据进行预测，选取高置信度的预测结果。标签扩展：将高置信度的未标记数据及其预测标签加入到标记数据集中。迭代训练：使用扩展后的标记数据集重新训练模型，重复上述步骤直到收敛。

优势与挑战

自训练方法简单易行，适用于多种模型和任务。然而，它依赖于初始模型的性能，如果初始模型性能较差，可能会引入错误的标签，导致错误的积累和模型性能下降。

一致性正则化（Consistency Regularization）

一致性正则化方法通过施加扰动，使模型对输入数据的微小变化保持鲁棒性。其核心思想是模型在面对相似的输入时应该产生相似的输出。

典型方法

Π模型（Π Model）：对输入数据添加噪声，通过最小化同一数据点不同扰动下的预测输出之间的差异来训练模型。

Mean Teacher：使用一个教师模型和一个学生模型，教师模型的参数是学生模型参数的指数滑动平均（EMA）。学生模型对输入数据添加噪声，教师模型对原始输入进行预测，通过最小化两者的预测差异来训练学生模型。

生成对抗网络（GANs）在半监督学习中的应用

生成对抗网络（Generative Adversarial Networks, GANs）通过生成器和判别器之间的对抗训练来生成逼真的数据样本。在半监督学习中，GANs不仅可以生成未标记数据，还可以利用生成的样本来改进分类器的性能。

典型方法

Semi-Supervised GAN：在标准GAN框架中，判别器不仅区分真实数据和生成数据，还将真实数据分为标记类别。生成器通过生成逼真的数据来欺骗判别器，从而提升分类器的性能。

Triple GAN：引入第三个网络——分类器，与生成器和判别器一起进行对抗训练，生成器生成的样本不仅需要欺骗判别器，还需要使分类器的预测结果与真实标签一致。

小结

常见的半监督学习算法各有千秋，适用于不同的应用场景和数据特征。图形半监督学习通过数据点之间的连接关系传播标签信息；自训练方法简单易行，适用于多种任务；一致性正则化通过增强模型鲁棒性提升性能；GANs 在半监督学习中的应用充分利用生成数据来改进分类器。这些方法在实际应用中常常结合使用，以期获得更好的模型性能和泛化能力。

三、常见的半监督学习算法代码实战

在本章节中，我们将通过代码实战展示如何使用 PyTorch 实现常见的半监督学习算法，包括图形半监督学习、自训练、一致性正则化和生成对抗网络（GANs）。我们将通过详细的代码和注释，帮助读者深入理解这些算法的实现细节和工作原理。

1. 图形半监督学习

图形半监督学习通过构建数据点之间的图结构，利用图上的连接关系来传播标签信息。以下是一个基于 PyTorch 实现的简单图正则化算法示例。

数据准备

我们将使用一个小型的合成数据集来演示图形半监督学习的实现。

<code>import numpy as np

import torch

import torch.nn as nn

import torch.optim as optim

from sklearn.datasets import make_moons

from sklearn.preprocessing import StandardScaler

# 生成合成数据集

X, y = make_moons(n_samples=200, noise=0.1)

scaler = StandardScaler()

X = scaler.fit_transform(X)

# 将数据分为标记和未标记数据

n_labeled = 20

X_labeled = torch.tensor(X[:n_labeled], dtype=torch.float32)

y_labeled = torch.tensor(y[:n_labeled], dtype=torch.long)

X_unlabeled = torch.tensor(X[n_labeled:], dtype=torch.float32)

模型定义

我们定义一个简单的两层全连接神经网络作为基础模型。

class MLP(nn.Module):

def __init__(self, input_dim, hidden_dim, output_dim):

super(MLP, self).__init__()

self.fc1 = nn.Linear(input_dim, hidden_dim)

self.fc2 = nn.Linear(hidden_dim, output_dim)

def forward(self, x):

x = torch.relu(self.fc1(x))

x = self.fc2(x)

return x

model = MLP(input_dim=2, hidden_dim=16, output_dim=2)

图正则化

构建图结构，并定义图正则化的损失函数。

from sklearn.neighbors import kneighbors_graph

# 构建K近邻图

knn_graph = kneighbors_graph(X, n_neighbors=10, mode='connectivity')code>

adj_matrix = torch.tensor(knn_graph.toarray(), dtype=torch.float32)

# 定义图正则化损失

def graph_regularization(model, X, adj_matrix):

output = model(X)

diff = output.unsqueeze(1) - output.unsqueeze(0)

loss = (diff**2 * adj_matrix).sum()

return loss

# 定义总损失函数

criterion = nn.CrossEntropyLoss()

def total_loss(model, X_labeled, y_labeled, X_unlabeled, adj_matrix, lambda_reg):

labeled_loss = criterion(model(X_labeled), y_labeled)

reg_loss = graph_regularization(model, torch.cat((X_labeled, X_unlabeled)), adj_matrix)

return labeled_loss + lambda_reg * reg_loss

模型训练

训练模型，并应用图正则化。

optimizer = optim.Adam(model.parameters(), lr=0.01)

lambda_reg = 0.1

for epoch in range(100):

optimizer.zero_grad()

loss = total_loss(model, X_labeled, y_labeled, X_unlabeled, adj_matrix, lambda_reg)

loss.backward()

optimizer.step()

if (epoch + 1) % 10 == 0:

print(f'Epoch [{ epoch + 1}/100], Loss: { loss.item():.4f}')

2. 自训练

自训练通过迭代的方式，逐步将高置信度的未标记数据加入到标记数据集中，重新训练模型。

数据准备

使用与前面相同的数据集。

# 使用与前面相同的数据集

模型定义

使用相同的 MLP 模型。

# 使用相同的 MLP 模型

自训练

定义自训练的迭代过程。

from torch.utils.data import DataLoader, TensorDataset

# 初始训练

dataset = TensorDataset(X_labeled, y_labeled)

dataloader = DataLoader(dataset, batch_size=16, shuffle=True)

criterion = nn.CrossEntropyLoss()

optimizer = optim.Adam(model.parameters(), lr=0.01)

def train_model(model, dataloader, optimizer, criterion, epochs=100):

for epoch in range(epochs):

for X_batch, y_batch in dataloader:

optimizer.zero_grad()

output = model(X_batch)

loss = criterion(output, y_batch)

loss.backward()

optimizer.step()

train_model(model, dataloader, optimizer, criterion)

# 自训练迭代

for iteration in range(5):

# 预测未标记数据

with torch.no_grad():

outputs = model(X_unlabeled)

confidences, pseudo_labels = torch.max(outputs, dim=1)

# 选取高置信度的样本

high_confidence_mask = confidences > 0.9

X_pseudo_labeled = X_unlabeled[high_confidence_mask]

y_pseudo_labeled = pseudo_labels[high_confidence_mask]

# 扩展标记数据集

X_labeled = torch.cat((X_labeled, X_pseudo_labeled))

y_labeled = torch.cat((y_labeled, y_pseudo_labeled))

# 重新训练模型

dataset = TensorDataset(X_labeled, y_labeled)

dataloader = DataLoader(dataset, batch_size=16, shuffle=True)

train_model(model, dataloader, optimizer, criterion)

print(f'Iteration [{ iteration + 1}/5] completed')

3. 一致性正则化

一致性正则化通过施加扰动，使模型对输入数据的微小变化保持鲁棒性。

数据准备

使用与前面相同的数据集。

# 使用与前面相同的数据集

模型定义

使用相同的 MLP 模型。

# 使用相同的 MLP 模型

一致性正则化

定义一致性正则化的损失函数，并训练模型。

# 定义一致性正则化损失

def consistency_loss(model, X, noise_factor=0.1):

X_noisy = X + noise_factor * torch.randn_like(X)

output = model(X)

output_noisy = model(X_noisy)

return ((output - output_noisy)**2).mean()

# 总损失函数

def total_loss(model, X_labeled, y_labeled, X_unlabeled, lambda_reg):

labeled_loss = criterion(model(X_labeled), y_labeled)

reg_loss = consistency_loss(model, X_unlabeled)

return labeled_loss + lambda_reg * reg_loss

# 训练模型

optimizer = optim.Adam(model.parameters(), lr=0.01)

lambda_reg = 0.1

for epoch in range(100):

optimizer.zero_grad()

loss = total_loss(model, X_labeled, y_labeled, X_unlabeled, lambda_reg)

loss.backward()

optimizer.step()

if (epoch + 1) % 10 == 0:

print(f'Epoch [{ epoch + 1}/100], Loss: { loss.item():.4f}')

4. 生成对抗网络（GANs）

GANs 通过生成器和判别器之间的对抗训练来生成逼真的数据样本，并利用这些样本改进分类器的性能。

数据准备

使用与前面相同的数据集。

# 使用与前面相同的数据集

模型定义

定义生成器和判别器模型。

class Generator(nn.Module):

def __init__(self, input_dim, hidden_dim, output_dim):

super(Generator, self).__init__()

self.fc1 = nn.Linear(input_dim, hidden_dim)

self.fc2 = nn.Linear(hidden_dim, output_dim)

def forward(self, z):

x = torch.relu(self.fc1(z))

x = torch.tanh(self.fc2(x))

return x

class Discriminator(nn.Module):

def __init__(self, input_dim, hidden_dim, output_dim):

super(Discriminator, self).__init__()

self.fc1 = nn.Linear(input_dim, hidden_dim)

self.fc2 = nn.Linear(hidden_dim, output_dim)

def forward(self, x):

x = torch.relu(self.fc1(x))

x = torch.sigmoid(self.fc2(x))

return x

generator = Generator(input_dim=2, hidden_dim=16, output_dim=2)

discriminator = Discriminator(input_dim=2, hidden_dim=16, output_dim=1)

训练 GANs

定义 GANs 的损失函数，并进行对抗训练。

# 定义损失函数

adversarial_loss = nn.BCELoss()

# 优化器

optimizer_G = optim.Adam(generator.parameters(), lr=0.01)

optimizer_D = optim.Adam(discriminator.parameters(), lr=0.01)

# 训练 GANs

num_epochs = 100

for epoch in range(num_epochs):

# 训练判别器

optimizer_D.zero_grad()

# 真实数据

real_data = torch.tensor(X, dtype=torch.float32)

real_labels = torch.ones(real_data.size(0), 1)

real_output = discriminator(real_data)

d_loss_real = adversarial_loss(real_output, real_labels)

# 生成数据

z = torch.randn(real_data.size(0), 2)

fake_data = generator(z)

fake_labels = torch.zeros(real_data.size(0), 1)

fake_output = discriminator(fake_data.detach())

d_loss_fake = adversarial_loss(fake_output, fake_labels)

# 总判别器损失

d_loss = d_loss_real + d_loss_fake

d_loss.backward()

optimizer_D.step()

# 训练生成器

optimizer_G.zero_grad()

fake_output = discriminator(fake_data)

g_loss = adversarial_loss(fake_output, real_labels)

g_loss.backward()

optimizer_G.step()

if (epoch + 1) % 10 == 0:

print(f'Epoch [{ epoch + 1}/100], D Loss: { d_loss.item():.4f}, G Loss: { g_loss.item():.4f}')

小结

本章节通过代码实战展示了如何使用 PyTorch 实现图形半监督学习、自训练、一致性正则化和生成对抗网络（GANs）在半监督学习中的应用。每种方法通过详细的代码和注释，帮助读者深入理解这些算法的实现细节和工作原理。希望通过这些实战案例，读者能够更好地掌握半监督学习的核心思想和技术，实现自己的半监督学习模型。