本文详细介绍了强化学习的基础知识和基本算法，包括动态规划、蒙特卡洛方法和时序差分学习，解析了其核心概念、算法步骤及实现细节。

关注作者，复旦AI博士，分享AI领域全维度知识与研究。拥有10+年AI领域研究经验、复旦机器人智能实验室成员，国家级大学生赛事评审专家，发表多篇SCI核心期刊学术论文，上亿营收AI产品研发负责人。

一、导论

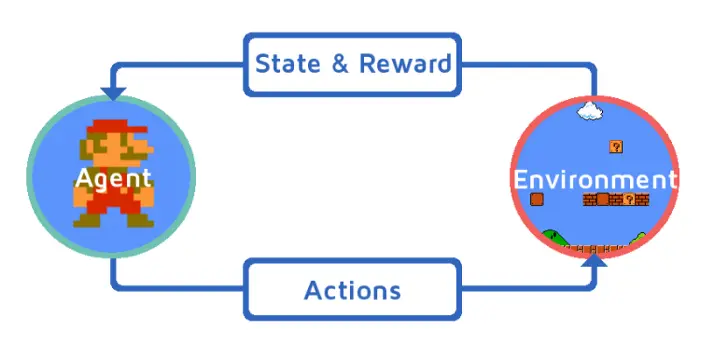
强化学习（Reinforcement Learning, RL）是机器学习中的一个重要分支，其目标是通过与环境的交互来学习决策策略，以最大化长期累积奖励。在强化学习中，智能体（agent）通过执行一系列动作来影响环境，从而获得反馈信号，即奖励（reward）。这种学习机制模仿了生物体在自然界中的学习过程，因此具有很强的现实意义和应用前景。

强化学习已经在多个领域展示了其强大的能力，以下是几个典型的应用场景：

游戏中的强化学习

游戏是强化学习的一个重要应用领域，特别是在复杂的策略游戏中，RL算法已经取得了显著的成功。例如，AlphaGo利用深度强化学习和蒙特卡洛树搜索（Monte Carlo Tree Search, MCTS）技术，在围棋比赛中击败了世界顶级棋手。此外，DQN（Deep Q-Network）在 Atari 游戏中的表现也证明了强化学习在复杂策略环境中的潜力。

自动驾驶

自动驾驶汽车需要在复杂的交通环境中做出实时决策，强化学习在这一领域具有重要的应用价值。通过不断与模拟环境交互，RL算法可以学习如何处理各种驾驶场景，包括避障、变道和停车等，从而提高自动驾驶系统的安全性和效率。

机器人控制

机器人控制是另一个重要的应用领域，强化学习可以帮助机器人在未知或动态环境中自主学习如何完成任务。例如，通过RL算法，机器人可以学会行走、抓取物体、组装零件等任务，这为实现高效灵活的机器人系统提供了新的途径。

二、基础知识

在理解强化学习的高级算法和应用之前，我们需要掌握其基础知识。基础知识部分将详细介绍强化学习的定义和关键术语、马尔可夫决策过程（MDP）的数学框架，以及策略与价值函数的定义和区别。这些概念是理解和应用强化学习的基石。

2.1 强化学习的定义和关键术语

强化学习（Reinforcement Learning, RL）是一种通过与环境交互来学习策略的机器学习方法。智能体（agent）在环境（environment）中执行动作（action），从而改变环境的状态（state）并获取奖励（reward）。智能体的目标是通过学习策略（policy），在不同状态下选择最佳动作，以最大化累积奖励。

2.1.1 关键术语

• 智能体（Agent）： 在环境中执行动作并学习策略的主体。
• 环境（Environment）： 智能体所处的外部系统，智能体的动作会影响环境的状态。
• 状态（State, S）： 环境在某一时刻的描述，通常由一组变量表示。
• 动作（Action, A）： 智能体在特定状态下可以执行的行为。
• 奖励（Reward, R）： 环境对智能体动作的反馈信号，表示动作的好坏。
• 策略（Policy, π）： 指导智能体在各个状态下选择动作的规则，可以是确定性的（π(s) = a）或随机的（π(a|s) = P(a|s)）。
• 价值函数（Value Function, V）： 用来估计智能体在某个状态或状态-动作对下的长期回报。
• 动作价值函数（Action-Value Function, Q）： 用来估计智能体在某个状态下执行某个动作后的长期回报。

2.2 马尔可夫决策过程（MDP）

马尔可夫决策过程（Markov Decision Process, MDP）是强化学习问题的数学框架。MDP通过五元组 (S, A, P, R, γ) 来描述，其中：

• S： 状态空间，表示所有可能状态的集合。
• A： 动作空间，表示智能体可以执行的所有动作的集合。
• P： 状态转移概率矩阵，P(s'|s,a) 表示在状态 s 执行动作 a 后转移到状态 s' 的概率。
• R： 奖励函数，R(s,a) 表示在状态 s 执行动作 a 后获得的即时奖励。
• γ： 折扣因子，0 ≤ γ ≤ 1，用于度量未来奖励的当前价值。

2.2.1 MDP的性质

MDP具有马尔可夫性质，即当前状态的转移只依赖于当前状态和当前动作，而与之前的状态无关。这一性质简化了强化学习问题的求解，使得智能体可以通过递推方式计算最优策略和价值函数。

2.2.2 状态转移与奖励

状态转移和奖励是MDP的核心，决定了智能体与环境的交互方式。状态转移概率矩阵 P 定义了环境的动态行为，而奖励函数 R 则评估了智能体动作的效果。通过不断试验和观察，智能体可以逐渐学会如何在不同状态下选择动作，以实现长期回报的最大化。

2.3 策略与价值函数

策略（Policy）和价值函数（Value Function）是强化学习中的两个关键概念，它们分别描述了智能体的行为规则和状态的价值评估。

2.3.1 策略（Policy, π）

策略 π 定义了智能体在每个状态下选择动作的规则。策略可以是确定性的，也可以是随机的。确定性策略 π(s) = a 表示在状态 s 下总是选择动作 a，而随机策略 π(a|s) = P(a|s) 则表示在状态 s 下以概率 P(a|s) 选择动作 a。

策略的目标是指导智能体选择最优动作，从而最大化累积奖励。学习最优策略是强化学习的核心任务之一。

2.3.2 价值函数（Value Function, V）

价值函数 V 用来估计某个状态或状态-动作对的长期回报。价值函数的定义有两种形式：

2.3.3 贝尔曼方程

贝尔曼方程提供了计算价值函数的递归公式，是求解最优策略和价值函数的基础。

三、基本算法

强化学习中，算法的设计和实现是智能体能够学习和优化策略的关键。基本算法包括动态规划（Dynamic Programming, DP）、蒙特卡洛方法（Monte Carlo Methods）和时序差分（Temporal-Difference, TD）学习。这些算法各有特点，适用于不同的场景和问题。

3.1 动态规划（Dynamic Programming, DP）

动态规划是一种通过递推方式求解优化问题的算法。在强化学习中，动态规划用于计算最优策略和价值函数。动态规划的前提是模型已知，即环境的状态转移概率和奖励函数是已知的。

3.1.1 价值迭代（Value Iteration）

价值迭代是一种通过不断更新价值函数来逼近最优价值函数的方法。其核心思想是利用贝尔曼最优方程递归地更新状态价值函数，直到收敛。

算法步骤：

代码示例：

<code>import numpy as np

def value_iteration(P, R, gamma, theta):

V = np.zeros(len(P))

while True:

delta = 0

for s in range(len(P)):

v = V[s]

V[s] = max(sum([P[s][a][s'] * (R[s][a] + gamma * V[s']) for s' in range(len(P))]) for a in range(len(P[s])))

delta = max(delta, abs(v - V[s]))

if delta < theta:

break

policy = np.zeros(len(P), dtype=int)

for s in range(len(P)):

policy[s] = np.argmax([sum([P[s][a][s'] * (R[s][a] + gamma * V[s']) for s' in range(len(P))]) for a in range(len(P[s]))])

return V, policy

# 示例用法

P = [[[0.8, 0.2], [0.1, 0.9]], [[0.7, 0.3], [0.2, 0.8]]]

R = [[1, 0], [0, 1]]

gamma = 0.9

theta = 1e-6

V, policy = value_iteration(P, R, gamma, theta)

print("Value Function:", V)

print("Policy:", policy)

3.1.2 策略迭代（Policy Iteration）

策略迭代通过交替进行策略评估和策略改进来找到最优策略。其核心思想是基于当前策略计算价值函数，然后改进策略，直到策略不再改变。

算法步骤：

代码示例：

<code>def policy_iteration(P, R, gamma, theta):

policy = np.zeros(len(P), dtype=int)

V = np.zeros(len(P))

def policy_evaluation(policy):

while True:

delta = 0

for s in range(len(P)):

v = V[s]

a = policy[s]

V[s] = sum([P[s][a][s'] * (R[s][a] + gamma * V[s']) for s' in range(len(P))])

delta = max(delta, abs(v - V[s]))

if delta < theta:

break

while True:

policy_stable = True

policy_evaluation(policy)

for s in range(len(P)):

old_action = policy[s]

policy[s] = np.argmax([sum([P[s][a][s'] * (R[s][a] + gamma * V[s']) for s' in range(len(P))]) for a in range(len(P[s]))])

if old_action != policy[s]:

policy_stable = False

if policy_stable:

break

return V, policy

# 示例用法

V, policy = policy_iteration(P, R, gamma, theta)

print("Value Function:", V)

print("Policy:", policy)

3.2 蒙特卡洛方法（Monte Carlo Methods）

蒙特卡洛方法是一种基于随机采样的强化学习方法。它通过多次模拟智能体与环境的交互过程，来估计状态价值或动作价值。与动态规划不同，蒙特卡洛方法不需要已知的环境模型，因此适用于模型未知的情况。

3.2.1 首访蒙特卡洛（First-Visit Monte Carlo）

首访蒙特卡洛方法通过记录智能体在每个状态第一次访问时的回报，来估计状态价值函数。具体步骤如下：

算法步骤：

代码示例：

<code>def first_visit_mc(env, num_episodes, gamma):

V = np.zeros(env.observation_space.n)

N = np.zeros(env.observation_space.n)

for _ in range(num_episodes):

state = env.reset()

trajectory = []

done = False

while not done:

action = env.action_space.sample()

next_state, reward, done, _ = env.step(action)

trajectory.append((state, action, reward))

state = next_state

visited_states = set()

G = 0

for state, action, reward in reversed(trajectory):

G = reward + gamma * G

if state not in visited_states:

visited_states.add(state)

N[state] += 1

V[state] += (G - V[state]) / N[state]

return V

# 示例用法

import gym

env = gym.make('FrozenLake-v1')

num_episodes = 5000

gamma = 0.9

V = first_visit_mc(env, num_episodes, gamma)

print("Value Function:", V)

3.2.2 每次访问蒙特卡洛（Every-Visit Monte Carlo）

每次访问蒙特卡洛方法通过记录智能体在每个状态每次访问时的回报，来估计状态价值函数。具体步骤如下：

算法步骤：

代码示例：

<code>def every_visit_mc(env, num_episodes, gamma):

V = np.zeros(env.observation_space.n)

N = np.zeros(env.observation_space.n)

for _ in range(num_episodes):

state = env.reset()

trajectory = []

done = False

while not done:

action = env.action_space.sample()

next_state, reward, done, _ = env.step(action)

trajectory.append((state, action, reward))

state = next_state

G = 0

for state, action, reward in reversed(trajectory):

G = reward + gamma * G

N[state] += 1

V[state] += (G - V[state]) / N[state]

return V

# 示例用法

V = every_visit_mc(env, num_episodes, gamma)

print("Value Function:", V)

3.3 时序差分（Temporal-Difference, TD）学习

时序差分学习结合了蒙特卡洛方法和动态规划的优点。它既不需要完整的轨迹，也不需要已知的环境模型，通过每一步的经验更新价值函数。

3.3.1 SARSA（State-Action-Reward-State-Action）

SARSA 是一种基于策略的 TD 学习算法，其名称代表了五元组 ((S_t, A_t, R_{t+1}, S_{t+1}, A_{t+1}))。SARSA 通过每一步的经验更新动作价值函数。

算法步骤：

代码示例：

<code>def sarsa(env, num_episodes, alpha, gamma, epsilon):

Q = np.zeros((env.observation_space.n, env.action_space.n))

def epsilon_greedy_policy(state):

if np.random.rand() < epsilon:

return np.random.choice(env.action_space.n)

else:

return np.argmax(Q[state])

for _ in range(num_episodes):

state = env.reset()

action = epsilon_greedy_policy(state)

done = False

while not done:

next_state, reward, done, _ = env.step(action)

next_action = epsilon_greedy_policy(next_state)

Q[state, action] += alpha * (reward + gamma * Q[next_state, next_action] - Q[state, action])

state, action = next_state, next_action

return Q

# 示例用法

alpha = 0.1

Q = sarsa(env, num_episodes, alpha, gamma, epsilon)

print("Q-Value Function:", Q)

3.3.2 Q学习（Q-Learning）

Q学习是一种无策略的 TD 学习算法，其目标是直接逼近最优动作价值函数。Q学习通过每一步的经验更新 Q 值函数，但不同于 SARSA，Q学习使用最大化未来 Q 值的动作来更新当前 Q 值。

算法步骤：

代码示例：

<code>def q_learning(env, num_episodes, alpha, gamma, epsilon):

Q = np.zeros((env.observation_space.n, env.action_space.n))

def epsilon_greedy_policy(state):

if np.random.rand() < epsilon:

return np.random.choice(env.action_space.n)

else:

return np.argmax(Q[state])

for _ in range(num_episodes):

state = env.reset()

done = False

while not done:

action = epsilon_greedy_policy(state)

next_state, reward, done, _ = env.step(action)

Q[state, action] += alpha * (reward + gamma * np.max(Q[next_state]) - Q[state, action])

state = next_state

return Q

# 示例用法

Q = q_learning(env, num_episodes, alpha, gamma, epsilon)

print("Q-Value Function:", Q)

本文由博客一文多发平台 OpenWrite 发布！