目录

一、特征选择1、定义2、原因3、做法4、生成过程5、停止条件

二、特征提取三、PCA 算法1、零均值化（中心化）2、方差3、协方差4、协方差矩阵5、对协方差矩阵求特征值、特征矩阵6、对特征值进行排序7、评价模型8、代码实现9、sklearn 库10、鸢尾花实例11、优缺点

一、特征选择

1、定义

从 N 个特征中选择其中 M（M<=N）个子特征，并且在 M 个子特征中，准则函数（实现目标）可以达到最优解。

卷积负责提取图像中的局部特征。

特征选择想要做的是：

选择尽可能少的子特征，模型的效果不会显著下降，并且结果的类别分布尽可能的接近真实的类别分布。

2、原因

在现实生活中，一个对象往往具有很多属性（以下称为特征），这些特征大致可以被分成三种主要的类型：

相关特征：对于学习任务（例如分类问题）有帮助，可以提升学习算法的效果。

无关特征：对于我们的算法没有任何帮助，不会给算法的效果带来任何提升。

冗余特征：不会对我们的算法带来新的信息，或者这种特征的信息可以由其它的特征推断出。

同一特征在不同业务场景下可以是不同类型的特征。

但是对于一个特定的学习算法来说，哪一个特征是有效的是未知的。因此，需要从所有特征中选择出对于学习算法有益的相关特征。

进行特征选择的主要目的：

降维（例如把100个特征减少为50个）降低学习任务的难度提升模型的效率

3、做法

特征选择主要包括四个过程：

生成过程：生成候选的特征子集。评价函数：评价特征子集的好坏。停止条件：决定什么时候该停止。验证过程：特征子集是否有效。

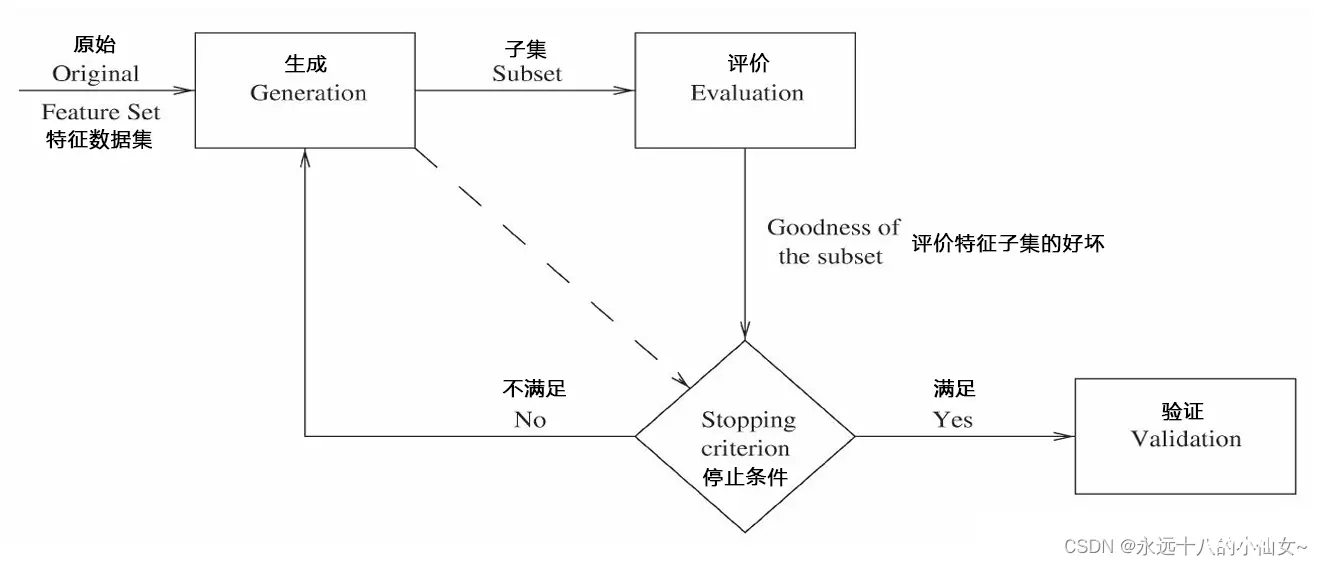
4、生成过程

生成过程是一个搜索过程，这个过程主要有以下三个策略：

完全搜索：根据评价函数做完全搜索。完全搜索主要分为穷举搜索和非穷举搜索。启发式搜索：根据一些启发式规则在每次迭代时，决定剩下的特征是应该被选择还是被拒绝。这种方法很简单并且速度很快。随机搜索：每次迭代时会设置一些参数，参数的选择会影响特征选择的效果。由于会设置一些参数（例如最大迭代次数）。

5、停止条件

停止条件用来决定迭代过程什么时候停止，生成过程和评价函数可能会对于怎么选择停止条件产生影响。停止条件有以下四种选择：

达到预定义的最大迭代次数。达到预定义的最大特征数。增加（删除）任何特征不会产生更好的特征子集。根据评价函数，产生最优特征子集。

二、特征提取

特征：常见的特征有边缘、角、区域等。

特征提取：是通过属性间的关系，如组合不同的属性得到新的属性，这样就改变了原来的特征空间。

特征选择：是从原始特征数据集中选择出子集，是一种包含的关系，没有更改原始的特征空间。

目前图像特征的提取主要有两种方法：

传统的特征提取方法：基于图像本身的特征进行提取。深度学习方法：基于样本自动训练出区分图像的特征分类器。

特征选择（feature selection）和特征提取（Feature extraction）都属于降维（Dimension reduction）。

三、PCA 算法

当我们处理高维数据时，往往存在冗余信息和噪声，这使得数据分析和模型训练变得更加困难。主成分分析（Principal Component Analysis，PCA）是一种常用的降维技术，通过线性变换将高维数据映射到低维空间，从而保留数据中最重要的信息。

原理

就是将数据从原始的空间中转换到新的特征空间中。

例如原始的空间是三维的 (x,y,z)，x、y、z 分别是原始空间的三个基，通过 PCA 算法，用新的坐标系 (a,b,c) 来表示原始的数据，那么 a、b、c 就是新的基，它们组成新的特征空间。

在新的特征空间中，可能所有的数据在 c 上的投影都接近于 0，即可以忽略，那么我们就可以直接用 (a,b) 来表示数据，这样数据就从三维的 (x,y,z) 降到了二维的 (a,b)。

步骤

1、对原始数据零均值化（中心化）。

2、求协方差矩阵。

3、对协方差矩阵求特征向量和特征值，这些特征向量组成了新的特征空间。

1、零均值化（中心化）

中心化即是指变量减去它的均值，使均值为0。

其实就是一个平移的过程，平移后使得所有数据的中心是(0,0)。

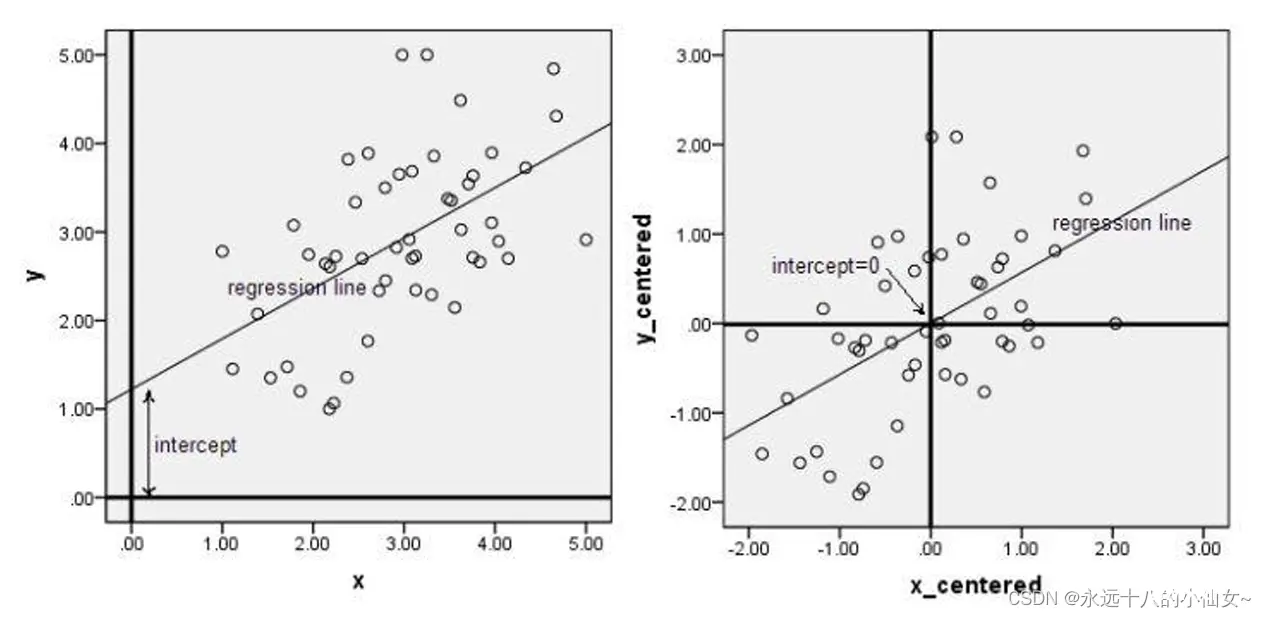
只有中心化数据之后，计算得到的方向才能比较好的“概括”原来的数据。此图形象的表述了，中心化的几何意义，就是将样本集的中心平移到坐标系的原点O上。

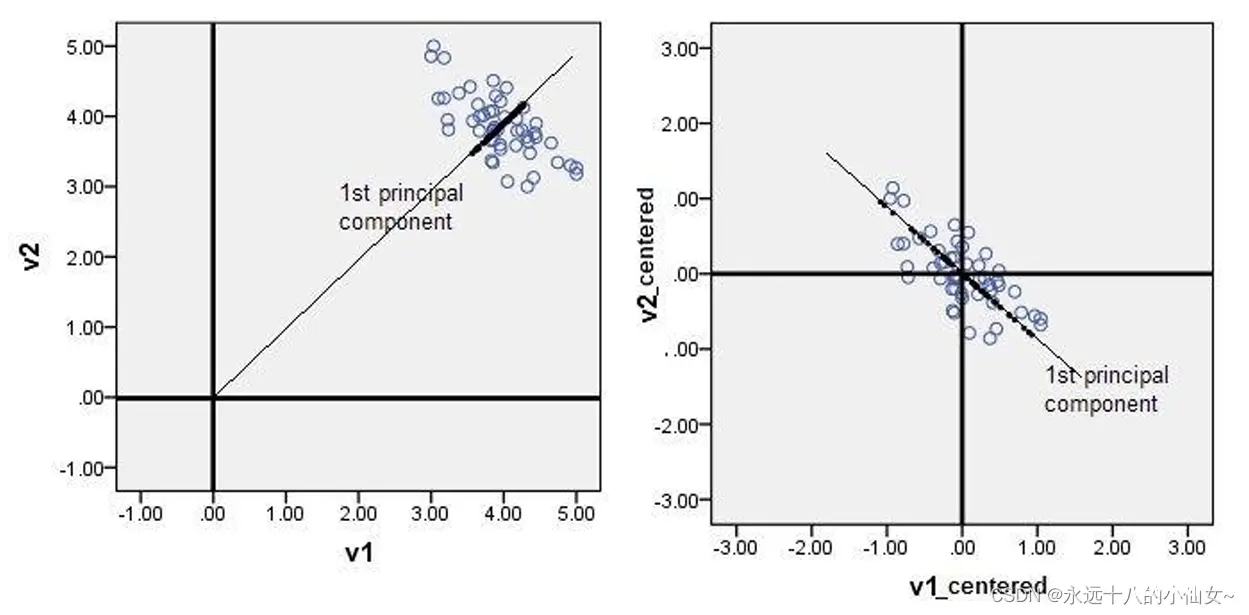
2、方差

对于一组数据，如果它在某一坐标轴上的方差越大，说明坐标点越分散，该属性能够比较好的反映源数据。

s

2

=

∑

i

=

1

n

(

X

i

−

X

ˉ

)

2

n

−

1

s^2 = \frac{\sum_{i=1}^{n} (X_i - \bar{X})^2}{n-1}

s2=n−1∑i=1n​(Xi​−Xˉ)2​

PCA 算法的优化目标：

降维后同一维度的方差最大。

不同维度之间的相关性为 0。

3、协方差

协方差就是一种用来度量两个随机变量关系的统计量。

同一元素的协方差就表示该元素的方差，不同元素之间的协方差就表示它们的相关性。

Cov

(

X

,

Y

)

=

∑

i

=

1

n

(

X

i

−

X

ˉ

)

(

Y

i

−

Y

ˉ

)

n

−

1

\text{Cov}(X, Y) = \frac{\sum_{i=1}^{n} (X_i - \bar{X})(Y_i - \bar{Y})}{n-1}

Cov(X,Y)=n−1∑i=1n​(Xi​−Xˉ)(Yi​−Yˉ)​

协方差的性质：

1、Cov(X,Y) = Cov(Y,X)

2、Cov(aX,bY) = abCov(Y,X) (a,b是常数)

3、Cov(X1+X2,Y) = Cov(X1,Y)+Cov(X2,Y)

由Cov

(

X

,

Y

)

=

∑

i

=

1

n

(

X

i

−

X

ˉ

)

(

Y

i

−

Y

ˉ

)

n

−

1

和

s

2

=

∑

i

=

1

n

(

X

i

−

X

ˉ

)

2

n

−

1

可看出：

C

o

v

(

X

,

X

)

=

D

(

X

)

,

C

o

v

(

Y

,

Y

)

=

D

(

Y

)

同一元素的协方差等于方差

D

\text{由Cov}(X, Y) = \frac{\sum_{i=1}^{n} (X_i - \bar{X})(Y_i - \bar{Y})}{n-1}和s^2 = \frac{\sum_{i=1}^{n} (X_i - \bar{X})^2}{n-1} 可看出：\\ Cov(X,X)=D(X),Cov(Y,Y)=D(Y)\\ 同一元素的协方差等于方差D

由Cov(X,Y)=n−1∑i=1n​(Xi​−Xˉ)(Yi​−Yˉ)​和s2=n−1∑i=1n​(Xi​−Xˉ)2​可看出：Cov(X,X)=D(X),Cov(Y,Y)=D(Y)同一元素的协方差等于方差D

协方差衡量了两属性之间的关系：

当 Cov(X,Y)>0 时，表示 X 与 Y 正相关。

当 Cov(X,Y)<0 时，表示 X 与 Y 负相关。

当 Cov(X,Y)=0 时，表示 X 与 Y 不相关。

4、协方差矩阵

定义

C

=

(

c

i

j

)

n

×

n

=

[

c

11

c

12

…

c

1

n

c

21

c

22

…

c

2

n

⋮

⋮

⋱

⋮

c

n

1

c

n

2

…

c

n

n

]

c

i

j

=

C

o

v

(

X

i

,

X

j

)

,

i

,

j

=

1

,

2

,

.

.

.

,

n

C = (c_{ij})_{n \times n} = \begin{bmatrix} c_{11} & c_{12} & \ldots & c_{1n} \\ c_{21} & c_{22} & \ldots & c_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ c_{n1} & c_{n2} & \ldots & c_{nn} \end{bmatrix}\\ c_{ij}=Cov(X_i,X_j),i,j=1,2,...,n

C=(cij​)n×n​=

​c11​c21​⋮cn1​​c12​c22​⋮cn2​​……⋱…​c1n​c2n​⋮cnn​​

​cij​=Cov(Xi​,Xj​),i,j=1,2,...,n

比如，三维(x,y,z)的协方差矩阵：

C

=

[

Cov

(

x

,

x

)

Cov

(

x

,

y

)

Cov

(

x

,

z

)

Cov

(

y

,

x

)

Cov

(

y

,

y

)

Cov

(

y

,

z

)

Cov

(

z

,

x

)

Cov

(

z

,

y

)

Cov

(

z

,

z

)

]

C = \begin{bmatrix} \text{Cov}(x, x) & \text{Cov}(x, y) & \text{Cov}(x, z) \\ \text{Cov}(y, x) & \text{Cov}(y, y) & \text{Cov}(y, z) \\ \text{Cov}(z, x) & \text{Cov}(z, y) & \text{Cov}(z, z) \end{bmatrix}

C=

​Cov(x,x)Cov(y,x)Cov(z,x)​Cov(x,y)Cov(y,y)Cov(z,y)​Cov(x,z)Cov(y,z)Cov(z,z)​

​

特点

协方差矩阵计算的是不同维度之间的协方差，而不是不同样本之间的。样本矩阵的每行是一个样本，每列为一个维度，所以我们要按列计算均值。协方差矩阵的对角线就是各个维度上的方差。

特别的，如果做了中心化，则协方差矩阵为（中心化矩阵的协方差矩阵公式，m为样本个数）：

D

=

1

m

Z

T

Z

D=\frac{1}{m}Z^TZ

D=m1​ZTZ

5、对协方差矩阵求特征值、特征矩阵

A 为 n 阶矩阵，若数 λ 和 n 维非 0 列向量 x 满足 Ax=λx，那么数 λ 称为 A 的特征值，x 称为 A 的对应于特征值 λ 的特征向量。

式 Ax=λx 也可写成 ( A-λE)x=0，E 是单位矩阵，并且|A-λE|叫做 A 的特征多项式。当特征多项式等于 0 的时候，称为 A 的特征方程，特征方程是一个齐次线性方程组，求解特征值的过程其实就是求解特征方程的解。

对于协方差矩阵 A，其特征值（ 可能有多个）计算方法为：

∣

A

−

λ

E

∣

=

0

|A-λE|=0

∣A−λE∣=0

假设

A

=

[

3

2

1

4

]

E

为单位矩阵

,

E

=

[

1

0

0

1

]

带入公式

∣

A

−

λ

E

∣

=

0

后，

A

−

λ

E

=

[

3

−

λ

2

1

4

−

λ

]

行列式计算：

(

3

−

λ

)

(

4

−

λ

)

−

(

1

)

(

2

)

=

λ

2

−

7

λ

+

10

令行列式等于零并解出

λ

：

λ

2

−

7

λ

+

10

=

0

将二次方程进行因式分解：

(

λ

−

5

)

(

λ

−

2

)

=

0

得到两个

λ

的解：

λ

1

=

5

,

λ

2

=

2

因此，矩阵

A

的特征值为

5

和

2

根据

(

A

−

λ

E

)

x

=

0

求

x

的值：

对

λ

=

5

：

(

A

−

λ

E

)

x

=

[

−

2

2

1

−

1

]

x

=

0

得到

x

1

=

[

2

−

1

]

对

λ

=

2

：

(

A

−

λ

E

)

x

=

[

1

2

1

2

]

x

=

0

得到

x

2

=

[

1

−

1

]

假设 A = \begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix}\\ E 为单位矩阵, E = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\\ 带入公式 |A-λE|=0 后， A - λE = \begin{bmatrix} 3 - λ & 2 \\ 1 & 4 - λ \end{bmatrix}\\ 行列式计算：\\ (3 - λ)(4 - λ) - (1)(2) = λ^2 - 7λ + 10\\ 令行列式等于零并解出 λ：\\ λ^2 - 7λ + 10 = 0\\ 将二次方程进行因式分解：\\ (λ - 5)(λ - 2) = 0\\ 得到两个 λ 的解：\\ λ₁ = 5, λ₂ = 2\\ 因此，矩阵 A 的特征值为 5 和 2\\ 根据 (A-λE)x=0 求 x 的值：\\ 对 λ = 5：\\ (A-λE)x = \begin{bmatrix} -2 & 2 \\ 1 & -1 \end{bmatrix}x = 0\\ 得到 x₁ = \begin{bmatrix} 2 \\ -1 \end{bmatrix}\\ 对 λ = 2：\\ (A-λE)x = \begin{bmatrix} 1 & 2 \\ 1 & 2 \end{bmatrix}x = 0\\ 得到 x₂ = \begin{bmatrix} 1 \\ -1 \end{bmatrix}

假设A=[31​24​]E为单位矩阵,E=[10​01​]带入公式∣A−λE∣=0后，A−λE=[3−λ1​24−λ​]行列式计算：(3−λ)(4−λ)−(1)(2)=λ2−7λ+10令行列式等于零并解出λ：λ2−7λ+10=0将二次方程进行因式分解：(λ−5)(λ−2)=0得到两个λ的解：λ1​=5,λ2​=2因此，矩阵A的特征值为5和2根据(A−λE)x=0求x的值：对λ=5：(A−λE)x=[−21​2−1​]x=0得到x1​=[2−1​]对λ=2：(A−λE)x=[11​22​]x=0得到x2​=[1−1​]

对数字图像矩阵做特征值分解，其实是在提取这个图像中的特征，这些提取出来的特征是一个个的向量，即对应着特征向量。而这些特征在图像中到底有多重要，这个重要性则通过特征值来表示。

比如一个 100x100 的图像矩阵 A 分解之后，会得到一个 100x100 的特征向量组成的矩阵 Q，以及一个 100x100 的只有对角线上的元素不为 0 的矩阵 E，这个矩阵 E 对角线上的元素就是特征值，而且还是按照从大到小排列的（取模，对于单个数来说，其实就是取绝对值），也就是说这个图像 A 提取出来了 100 个特征，这 100 个特征的重要性由 100 个数字来表示，这 100 个数字存放在对角矩阵 E 中。

所以，特征向量其实反应的是矩阵 A 本身固有的一些特征，本来一个矩阵就是一个线性变换，当把这个矩阵作用于一个向量的时候，通常情况绝大部分向量都会被这个矩阵 A 变换得“面目全非”，但是偏偏刚好存在这么一些向量，被矩阵 A 变换之后居然还能保持原来的样子，于是这些向量就可以作为矩阵的核心代表了。

于是我们可以说：一个变换（即一个矩阵）可以由其特征值和特征向量完全表述，这是因为从数学上看，这个矩阵所有的特征向量组成了这个向量空间的一组基底。而矩阵作为变换的本质其实就是把一个基底下的东西变换到另一个基底表示的空间中。

6、对特征值进行排序

将特征值按照从大到小的排序，选择其中最大的 k 个，然后将其对应的 k 个特征向量分别作为列向量组成特征向量矩阵 Wnxk。

计算 XnewW，即将数据集 Xnew 投影到选取的特征向量上，这样就得到了我们需要的已经降为的数据集 XnewW。

7、评价模型

通过特征值的计算，我们可以得到主成分所占的百分比，用来衡量模型的好坏。

对于前 k 个特征值所保留下的信息量计算方法如下：

η

k

=

∑

j

=

1

k

λ

j

∑

j

=

1

n

λ

j

×

100

%

\eta_k =\frac{\sum_{j=1}^{k} \lambda_j}{ \sum_{j=1}^{n} \lambda_j} \times 100\%

ηk​=∑j=1n​λj​∑j=1k​λj​​×100%

8、代码实现

详细计算过程

<code>import numpy as np # 导入 NumPy 库，用于数组操作

class CPCA(object):

'''

用PCA求样本矩阵X的K阶降维矩阵Z

Note:请保证输入的样本矩阵X shape=(m, n)，m行样例，n个特征

'''

def __init__(self, X, K):

'''

:param X,训练样本矩阵X

:param K,X的降维矩阵的阶数，即X要特征降维成k阶

'''

self.X = X # 样本矩阵X

self.K = K # K阶降维矩阵的K值

self.centrX = [] # 矩阵X的中心化

self.C = [] # 样本集的协方差矩阵C

self.U = [] # 样本矩阵X的降维转换矩阵

self.Z = [] # 样本矩阵X的降维矩阵Z

self.centrX = self._centralized()

self.C = self._cov()

self.U = self._U()

self.Z = self._Z() # Z=XU求得

def _centralized(self):

'''矩阵X的中心化'''

print('样本矩阵X:\n', self.X)

centrX = []

mean = np.array([np.mean(attr) for attr in self.X.T]) # 样本集的特征均值

print('样本集的特征均值:\n', mean)

centrX = self.X - mean # 样本集的中心化

print('样本矩阵X的中心化centrX:\n', centrX)

return centrX

def _cov(self):

'''求样本矩阵X的协方差矩阵C'''

# 样本集的样例总数

ns = np.shape(self.centrX)[0]

# 样本矩阵的协方差矩阵C

C = np.dot(self.centrX.T, self.centrX) / (ns - 1)

print('样本矩阵X的协方差矩阵C:\n', C)

return C

def _U(self):

'''求X的降维转换矩阵U, shape=(n,k), n是X的特征维度总数，k是降维矩阵的特征维度'''

# 先求X的协方差矩阵C的特征值和特征向量

a, b = np.linalg.eig(self.C) # 特征值赋值给a，对应特征向量赋值给b。函数doc：https://docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.linalg.eig.html

print('样本集的协方差矩阵C的特征值:\n', a)

print('样本集的协方差矩阵C的特征向量:\n', b)

# 给出特征值降序的topK的索引序列

ind = np.argsort(-1 * a)

# 构建K阶降维的降维转换矩阵U

UT = [b[:, ind[i]] for i in range(self.K)]

U = np.transpose(UT)

print('%d阶降维转换矩阵U:\n' % self.K, U)

return U

def _Z(self):

'''按照Z=XU求降维矩阵Z, shape=(m,k), n是样本总数，k是降维矩阵中特征维度总数'''

Z = np.dot(self.X, self.U)

print('X shape:', np.shape(self.X))

print('U shape:', np.shape(self.U))

print('Z shape:', np.shape(Z))

print('样本矩阵X的降维矩阵Z:\n', Z)

return Z

if __name__ == '__main__':

'10样本3特征的样本集, 行为样例，列为特征维度'

X = np.array([[10, 15, 29],

[15, 46, 13],

[23, 21, 30],

[11, 9, 35],

[42, 45, 11],

[9, 48, 5],

[11, 21, 14],

[8, 5, 15],

[11, 12, 21],

[21, 20, 25]])

K = np.shape(X)[1] - 1

print('样本集(10行3列，10个样例，每个样例3个特征):\n', X)

pca = CPCA(X, K)

简化实现

import numpy as np # 导入 NumPy 库，用于数组操作

class PCA():

def __init__(self, n_components):

self.n_components = n_components

def fit_transform(self, X):

# 计算特征数量

self.n_features_ = X.shape[1]

# 对数据进行零均值化

X = X - X.mean(axis=0)

# 计算协方差矩阵

self.covariance = np.dot(X.T, X) / X.shape[0]

# 计算协方差矩阵的特征值和特征向量

eig_vals, eig_vectors = np.linalg.eig(self.covariance)

# 对特征值进行降序排序，并获取对应的索引

idx = np.argsort(-eig_vals)

# 提取前 n_components 个特征向量作为主成分

self.components_ = eig_vectors[:, idx[:self.n_components]]

# 将原始数据投影到主成分上

return np.dot(X, self.components_)

# 创建 PCA 类的实例，设置要保留的主成分数量为 2

pca = PCA(n_components=2)

# 创建一个输入矩阵 X，每一行代表一个样本，每一列代表一个特征

X = np.array([[-1, 2, 66, -1], [-2, 6, 58, -1], [-3, 8, 45, -2], [1, 9, 36, 1], [2, 10, 62, 1], [3, 5, 83, 2]])

# 对输入数据进行主成分分析，并返回降维后的数据

newX = pca.fit_transform(X)

# 打印降维后的数据

print(newX)

# [[ 7.96504337 -4.12166867]

# [ -0.43650137 -2.07052079]

# [-13.63653266 -1.86686164]

# [-22.28361821 2.32219188]

# [ 3.47849303 3.95193502]

# [ 24.91311585 1.78492421]]

9、sklearn 库

<code>import numpy as np # 导入 NumPy 库，用于数组操作

# pip install numpy scikit-learn

from sklearn.decomposition import PCA # 导入 scikit-learn 中的 PCA 模块，scikit-learn 是一个用于机器学习的库

X = np.array([[-1,2,66,-1], [-2,6,58,-1], [-3,8,45,-2], [1,9,36,1], [2,10,62,1], [3,5,83,2]]) # 导入数据，维度为4

pca = PCA(n_components=2) # 降到2维

pca.fit(X) # 训练

newX=pca.fit_transform(X) # 降维后的数据

# PCA(copy=True, n_components=2, whiten=False)

print(pca.explained_variance_ratio_) # 输出贡献率

print(newX) # 输出降维后的数据

10、鸢尾花实例

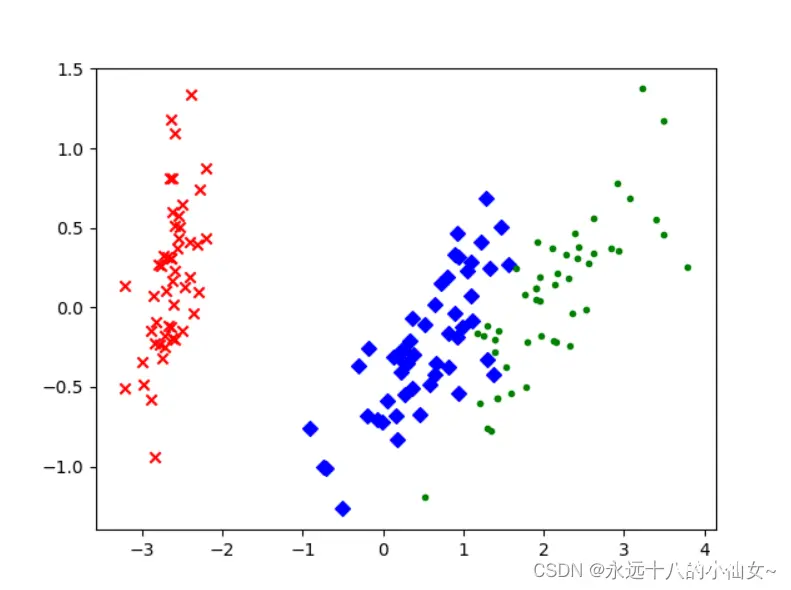
通过 Python 的 sklearn 库来实现鸢尾花数据进行降维，数据本身是 4 维的，降维后变成 2 维。

其中样本总数为 150，鸢尾花的类别有三种。

import matplotlib.pyplot as plt # 导入 Matplotlib 库，用于绘制图表

import sklearn.decomposition as dp # 导入 scikit-learn 中的 decomposition 模块，用于降维操作

from sklearn.datasets import load_iris # 导入 scikit-learn 中的 load_iris 函数，用于加载鸢尾花数据集

x,y=load_iris(return_X_y=True) # 加载数据，x表示数据集中的属性数据，y表示数据标签

pca=dp.PCA(n_components=2) # 加载pca算法，设置降维后主成分数目为2

reduced_x=pca.fit_transform(x) # 对原始数据进行降维，保存在reduced_x中

red_x,red_y=[],[]

blue_x,blue_y=[],[]

green_x,green_y=[],[]

for i in range(len(reduced_x)): # 按鸢尾花的类别将降维后的数据点保存在不同的表中

if y[i]==0:

red_x.append(reduced_x[i][0])

red_y.append(reduced_x[i][1])

elif y[i]==1:

blue_x.append(reduced_x[i][0])

blue_y.append(reduced_x[i][1])

else:

green_x.append(reduced_x[i][0])

green_y.append(reduced_x[i][1])

plt.scatter(red_x,red_y,c='r',marker='x')code>

plt.scatter(blue_x,blue_y,c='b',marker='D')code>

plt.scatter(green_x,green_y,c='g',marker='.')code>

plt.show()

11、优缺点