使用Python和scikit-learn实现支持向量机(SVM)
01_6 2024-09-07 12:01:04 阅读 97
支持向量机(Support Vector Machine,SVM)是一种强大的监督学习算法,广泛用于分类和回归问题。它能够有效处理线性和非线性数据,并在复杂数据集中表现出色。本文将介绍如何使用Python和scikit-learn库实现SVM,以及如何通过可视化不同参数设置来理解其工作原理。
一、什么是支持向量机(SVM)?
支持向量机是一种二类分类模型,它的基本思想是在特征空间中找到一个最优的超平面,能够将不同类别的数据点分隔开来,并且使得两侧距离最近的数据点(支持向量)到超平面的距离最大化。对于非线性可分的数据集,SVM通过核函数将数据映射到高维空间,使得数据线性可分。
二、实现步骤
我们将使用Python的scikit-learn库来实现一个简单的支持向量机分类器,并在一个合成的数据集上进行可视化展示。
1、导入必要的库和数据集生成
<code>from sklearn import svm
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
import numpy as np
2、定义绘制决策边界和支持向量的函数
# 定义绘制决策边界和支持向量的函数
def plot_hyperplane(clf, X, y, h=0.02, draw_sv=True, title='Hyperplane'):code>
# 确定绘图边界
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# 设置绘图属性
plt.title(title)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
# 生成网格数据并进行预测
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 绘制决策边界
plt.contourf(xx, yy, Z, cmap='hot', alpha=0.5)code>
# 定义不同类别的标记和颜色
markers = ['o', 's', '^']
colors = ['b', 'r', 'c']
labels = np.unique(y)
# 绘制数据点
for label in labels:
plt.scatter(X[y==label][:, 0],
X[y==label][:, 1],
c=colors[label],
marker=markers[label])
# 如果指定绘制支持向量,则绘制支持向量
if draw_sv:
sv = clf.support_vectors_
plt.scatter(sv[:, 0], sv[:, 1], c='y', marker='x')code>
3、生成合成数据集
使用make_moons函数生成一个合成的月亮形数据集,用于后续的分类器训练和可视化。
#生成包含150个样本的合成数据集,噪声为0.15
X, y = make_moons(n_samples=150, noise=0.15, random_state=42)
make_moons函数生成一个合成的月亮形状数据集。n_samples: 数据集样本数量。noise: 噪声水平,增加数据的随机性。random_state: 随机种子,确保每次运行生成的数据一致性。
4、初始化不同参数设置的SVM分类器
初始化了六个不同参数设置的SVM分类器,分别探索了不同的gamma和C参数组合对分类性能的影响。
# 初始化不同参数设置的SVM分类器
#初始化一个RBF核支持向量机分类器,设置参数C和gamma。
clf_rbf1 = svm.SVC(C=1, kernel='rbf', gamma=0.01)code>
clf_rbf2 = svm.SVC(C=1, kernel='rbf', gamma=5)code>
clf_rbf3 = svm.SVC(C=100, kernel='rbf', gamma=0.01)code>
clf_rbf4 = svm.SVC(C=100, kernel='rbf', gamma=5)code>
clf_rbf5 = svm.SVC(C=10000, kernel='rbf', gamma=0.01)code>
clf_rbf6 = svm.SVC(C=10000, kernel='rbf', gamma=5)code>
# 创建绘图区域
plt.figure()
# 将所有分类器放入列表中
clfs = [clf_rbf1, clf_rbf2, clf_rbf3, clf_rbf4, clf_rbf5, clf_rbf6]
# 设置每个子图的标题
titles = ['gamma=0.01, C=1',
'gamma=0.01, C=100',
'gamma=0.01, C=10000',
'gamma=5, C=1',
'gamma=5, C=100',
'gamma=5, C=10000']
初始化了六个不同参数设置的SVM分类器对象。svm.SVC: 创建一个支持向量机分类器。C: 正则化参数。kernel: 核函数类型,这里使用径向基函数(RBF)。gamma: RBF核函数的参数,影响决策边界的灵活性和复杂度。clfs: 包含所有分类器的列表。titles: 每个分类器对应的标题,用于在图表中显示参数设置。
5、绘制不同参数设置下的SVM决策边界
最后,我们通过循环遍历每个分类器,对其进行训练并绘制出相应的决策边界和支持向量。
# 对每个分类器进行训练和绘图
for clf, i in zip(clfs, range(len(clfs))):
clf.fit(X, y) # 训练分类器
plt.subplot(3, 2, i+1) # 创建3行2列的子图,并选择当前子图
plot_hyperplane(clf, X, y, title=titles[i]) # 绘制决策边界和支持向量
plt.show() # 显示图形
创建一个12x10英寸大小的图形窗口。使用zip函数将每个分类器clf与其对应的索引i组合。对每个分类器进行训练(clf.fit(X, y))并调用plot_hyperplane函数绘制决策边界。plt.subplot(3, 2, i+1): 将图形分成3行2列的子图,当前绘制第i+1个子图。plt.tight_layout(): 调整子图的布局,防止重叠。plt.show(): 显示绘制的图形。
三、结果分析
这幅图展示了使用较小的gamma(0.01)和较小的正则化参数C(1)训练的SVM模型。
决策边界相对平滑,模型的复杂度较低。
可以看到一些支持向量被标记为黄色的'x'符号。

这幅图展示了相同的低gamma值(0.01),但更大的正则化参数C(100)。
决策边界仍然平滑,但稍微更接近一些数据点,对噪声更敏感。

使用了极大的C值(10000),同时gamma仍然较低(0.01)。
决策边界非常接近许多数据点,模型非常复杂,几乎适应了每个数据点,可能存在过拟合的风险。

这幅图展示了较高的gamma值(5)和较小的正则化参数C(1)。
决策边界非常复杂,几乎适应了每个数据点,可能出现了过拟合。

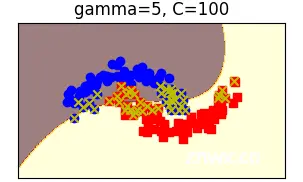
在高gamma(5)和较大C(100)的设置下,决策边界略有平滑化,但仍然相对复杂。

最后一幅图展示了高gamma(5)和非常大的C值(10000)。
决策边界非常复杂,几乎适应了每个数据点,存在严重的过拟合可能性。
总体分析:
参数gamma控制了决策边界的灵活性,较大的gamma值会导致决策边界更复杂,更贴近训练数据点。参数C是正则化参数,控制了对错误分类的惩罚,较大的C值会导致模型更关注训练数据,可能会导致过拟合。在低gamma和低C值的情况下,决策边界相对平滑,模型简单;而在高gamma和高C值的情况下,决策边界更复杂,可能会过度适应训练数据。
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。