波士顿房价预测案例（python scikit-learn）—多元线性回归(多角度实验分析)

这次实验，我们主要从以下几个方面介绍：

一、相关框架介绍

二、数据集介绍

三、实验结果-优化算法对比实验，数据标准化对比实验，正则化对比试验，多项式回归degree对比实验，岭回归alpha敏感度实验

一、相关框架介绍

Scikit-learn（全称：Simple and Efficient Tools for Machine Learning，意为“简单高效的机器学习工具”）是一个开源的Python机器学习库，它提供了简单而高效的工具，用于数据挖掘和数据分析。

Scikit-learn主要特点包括：丰富的算法库、易于使用、高效的性能、数据预处理和特征选择、模型评估和选择、可扩展性、社区支持。

二、数据集介绍

2.1数据集来源

波士顿房价数据集是一个著名的数据集，它在机器学习和统计分析领域中被广泛用于回归问题的实践和研究。这个数据集包含了美国马萨诸塞州波士顿郊区的房价信息，这些信息是由美国人口普查局收集的。

该数据集共包括507行数据，十三列特征，外加一列标签。

2.2数据集特征

数据集的特征：

CRIM: 城镇人均犯罪率 ZN: 占地面积超过25,000平方英尺的住宅用地比例

INDUS: 每个城镇非零售业务的比例 CHAS: 查尔斯河虚拟变量（如果是河道，则为1;否则为0）

NOX: 一氧化氮浓度（每千万份） RM: 每间住宅的平均房间数

AGE: 1940年以前建造的自住单位比例 DIS: 波士顿的五个就业中心加权距离

RAD: 径向高速公路的可达性指数 TAX: 每10,000美元的全额物业税率

PTRATIO: 城镇的学生与教师比例 B: 1000（Bk - 0.63）^ 2，其中Bk是城镇黑人的比例

LSTAT: 人口状况下降％ MEDV: 自有住房的中位数报价, 单位1000美元

三、实验结果-优化算法对比实验，数据标准化对比实验，正则化对比试验，多项式回归degree对比实验，岭回归alpha敏感度实验

3.1 优化算法对比实验

# 从 sklearn.datasets 导入波士顿房价数据读取器。from sklearn.datasets import load_boston# 从读取房价数据存储在变量 boston 中。boston = load_boston()# 输出数据描述。from matplotlib import pyplot as pltfrom matplotlib import font_managerfrom matplotlib import pyplot as pltimport numpy as npimport matplotlib# 参数设置import matplotlib.pyplot as pltplt.rcParams["font.sans-serif"]=["SimHei"] #设置字体plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题# 从sklearn.cross_validation 导入数据分割器。from sklearn.model_selection import train_test_split# 导入 numpy 并重命名为 np。import numpy as npfrom sklearn.linear_model import Ridge,LassoX = boston.datay = boston.target# 随机采样 25% 的数据构建测试样本，其余作为训练样本。X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)# 分析回归目标值的差异。print("The max target value is", np.max(boston.target))print("The min target value is", np.min(boston.target)) print("The average target value is", np.mean(boston.target))# 从 sklearn.preprocessing 导入数据标准化模块。from sklearn.preprocessing import StandardScalerfrom sklearn.preprocessing import MinMaxScalerfrom sklearn.preprocessing import Normalizer# 分别初始化对特征和目标值的标准化器。ss_X = StandardScaler()ss_y = StandardScaler()ss="StandardScaler"# 分别对训练和测试数据的特征以及目标值进行标准化处理。X_train = ss_X.fit_transform(X_train)X_test = ss_X.transform(X_test)y_train = ss_y.fit_transform(y_train.reshape(-1, 1))y_test = ss_y.transform(y_test.reshape(-1, 1))# 从 sklearn.linear_model 导入 LinearRegression。from sklearn.linear_model import LinearRegression# 使用默认配置初始化线性回归器 LinearRegression。def train_model(): lr = LinearRegression() # 使用训练数据进行参数估计。 lr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lr_y_predict = lr.predict(X_test) # 从 sklearn.linear_model 导入 SGDRegressor。 from sklearn.linear_model import SGDRegressor # 使用默认配置初始化线性回归器 SGDRegressor。 sgdr = SGDRegressor() # 使用训练数据进行参数估计。 sgdr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 sgdr_y_predict = sgdr.predict(X_test) ridge = Ridge(alpha=10) # 使用训练数据进行参数估计。 ridge.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 ridge_y_predict = ridge.predict(X_test) # Lasso lasso = Lasso(alpha=0.01) # 使用训练数据进行参数估计。 lasso.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lasso_y_predict = lasso.predict(X_test) return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict def evaluate(X_test,y_test,lr_y_predict,model):# 使用 LinearRegression 模型自带的评估模块，并输出评估结果。 nmse=model.score(X_test, y_test) print('The value of default measurement of LinearRegression is',nmse ) # 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。 from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error # 使用 r2_score 模块，并输出评估结果。 r2=r2_score(y_test, lr_y_predict) print('The value of R-squared of LinearRegression is',r2 ) # 使用 mean_squared_error 模块，并输出评估结果。 #print(y_test) lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1) #print(lr_y_predict) #print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))) mse=mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean squared error of LinearRegression is',mse ) # 使用 mean_absolute_error 模块，并输出评估结果。 mae= mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean absoluate error of LinearRegression is', mae ) return round(nmse,2),round(r2,2),round(mse,2),round(mae,2) def plot(model1,model2):# 数据 classes = [ 'r2', 'mse', 'mae'] # r2s = [87, 85, 89, 81, 78] # mess = [85, 98, 84, 79, 82] # nmse = [83, 85, 82, 87, 78] # 将横坐标班级先替换为数值 x = np.arange(len(classes)) width = 0.2 r2s_x = x mess_x = x + width nmse_x = x + 2 * width mae_x = x + 3 * width # 绘图 plt.bar(r2s_x, model1, width=width, color='gold', label='LinearRegression') plt.bar(mess_x,model2,width=width,color="silver",label="SGDRegressor") #plt.bar(nmse_x,model3,width=width, color="saddlebrown",label="ridge-alpha=10") #plt.bar(mae_x,model4,width=width, color="red",label="lasso-alpha=0.01") plt.title("lr,sdgr+"+ss+"性能对比图") #将横坐标数值转换为班级 plt.xticks(x + width, classes) #显示柱状图的高度文本 for i in range(len(classes)): plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8) plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8) #plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8) #plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8) #显示图例 plt.legend(loc="upper right") plt.show() #coding=gbk; def plot_line(X,y,model,name): #-------------------------------------------------------------- #z是我们生成的等差数列，用来画出线性模型的图形。 z=np.linspace(0,50,200).reshape(-1,1) plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k') plt.plot(z,z,c="k") plt.xlabel('y') plt.ylabel("y_hat") plt.title(name) plt.show() lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model()models=[lr,sgdr]r2s=[]mess=[]maes=[]nmse=[]results=[]plot_line(X,y,lr,'LinearRegression+'+ss)plot_line(X,y,sgdr,'SGDRegressor+'+ss)#plot_line(X,y,lasso,'lasso'+ss)#plot_line(X,y,ridge,'ridge'+ss)print("sgdr_y_predict")print(sgdr_y_predict)predicts=[lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict]i=0for model in models: result=evaluate(X_test,y_test,predicts[i],model) i=i+1 results.append(result) # r2s.append(result[1]) # mess.append(result[2]) # maes.append(result[3]) # nmse.append(result[0]) #evaluate(X_test,y_test,sgdr_y_predict,sgdr)print(results) #evaluate(X_test,y_test,sgdr_y_predict,sgdr)plot(results[0][1:4],results[1][1:4])

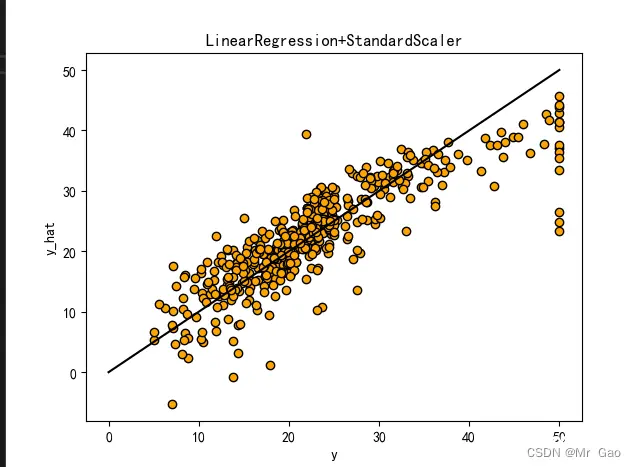
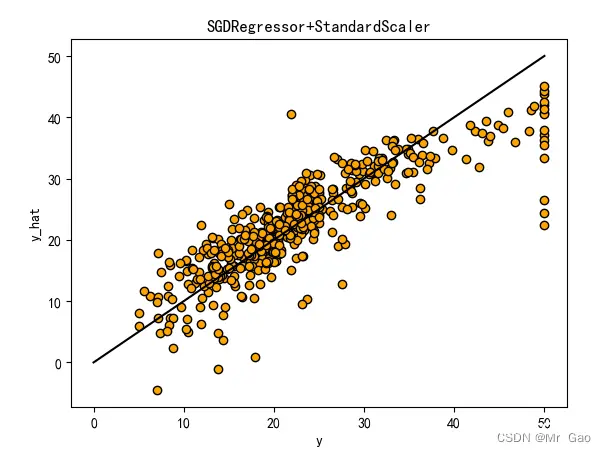
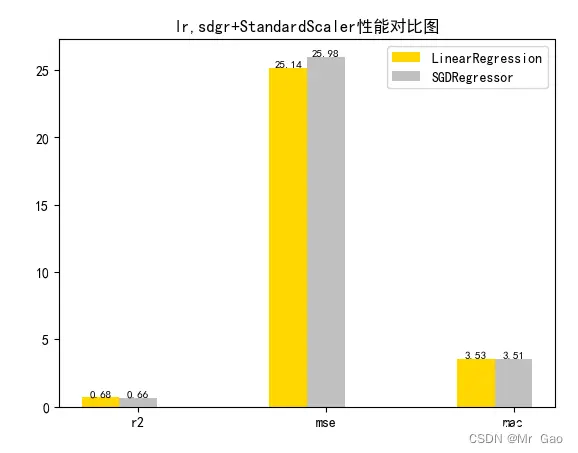
3.2 数据标准化对比实验

# 从 sklearn.datasets 导入波士顿房价数据读取器。from sklearn.datasets import load_boston# 从读取房价数据存储在变量 boston 中。boston = load_boston()# 输出数据描述。from matplotlib import pyplot as pltfrom matplotlib import font_managerfrom matplotlib import pyplot as pltimport numpy as npimport matplotlib# 参数设置import matplotlib.pyplot as pltplt.rcParams["font.sans-serif"]=["SimHei"] #设置字体plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题# 从sklearn.cross_validation 导入数据分割器。from sklearn.model_selection import train_test_split# 导入 numpy 并重命名为 np。import numpy as npfrom sklearn.linear_model import Ridge,LassoX = boston.datay = boston.target# 随机采样 25% 的数据构建测试样本，其余作为训练样本。X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)# 分析回归目标值的差异。print("The max target value is", np.max(boston.target))print("The min target value is", np.min(boston.target)) print("The average target value is", np.mean(boston.target))# 从 sklearn.preprocessing 导入数据标准化模块。from sklearn.preprocessing import StandardScalerfrom sklearn.preprocessing import MinMaxScalerfrom sklearn.preprocessing import Normalizer# 分别初始化对特征和目标值的标准化器。ss_X = StandardScaler()ss_y = StandardScaler()ss="StandardScaler"# 分别对训练和测试数据的特征以及目标值进行标准化处理。X_train = ss_X.fit_transform(X_train)X_test = ss_X.transform(X_test)y_train = ss_y.fit_transform(y_train.reshape(-1, 1))y_test = ss_y.transform(y_test.reshape(-1, 1))# 从 sklearn.linear_model 导入 LinearRegression。from sklearn.linear_model import LinearRegression# 使用默认配置初始化线性回归器 LinearRegression。def train_model(): lr = LinearRegression() # 使用训练数据进行参数估计。 lr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lr_y_predict = lr.predict(X_test) # 从 sklearn.linear_model 导入 SGDRegressor。 from sklearn.linear_model import SGDRegressor # 使用默认配置初始化线性回归器 SGDRegressor。 sgdr = SGDRegressor() # 使用训练数据进行参数估计。 sgdr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 sgdr_y_predict = sgdr.predict(X_test) ridge = Ridge(alpha=10) # 使用训练数据进行参数估计。 ridge.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 ridge_y_predict = ridge.predict(X_test) # Lasso lasso = Lasso(alpha=0.01) # 使用训练数据进行参数估计。 lasso.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lasso_y_predict = lasso.predict(X_test) return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict def evaluate(X_test,y_test,lr_y_predict,model):# 使用 LinearRegression 模型自带的评估模块，并输出评估结果。 nmse=model.score(X_test, y_test) print('The value of default measurement of LinearRegression is',nmse ) # 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。 from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error # 使用 r2_score 模块，并输出评估结果。 r2=r2_score(y_test, lr_y_predict) print('The value of R-squared of LinearRegression is',r2 ) # 使用 mean_squared_error 模块，并输出评估结果。 #print(y_test) lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1) #print(lr_y_predict) #print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))) mse=mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean squared error of LinearRegression is',mse ) # 使用 mean_absolute_error 模块，并输出评估结果。 mae= mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean absoluate error of LinearRegression is', mae ) return round(nmse,2),round(r2,2),round(mse,2),round(mae,2) def plot(model1,model2):# 数据 classes = [ 'r2', 'mse', 'mae'] # r2s = [87, 85, 89, 81, 78] # mess = [85, 98, 84, 79, 82] # nmse = [83, 85, 82, 87, 78] # 将横坐标班级先替换为数值 x = np.arange(len(classes)) width = 0.2 r2s_x = x mess_x = x + width nmse_x = x + 2 * width mae_x = x + 3 * width # 绘图 plt.bar(r2s_x, model1, width=width, color='gold', label='LinearRegression') plt.bar(mess_x,model2,width=width,color="silver",label="SGDRegressor") #plt.bar(nmse_x,model3,width=width, color="saddlebrown",label="ridge-alpha=10") #plt.bar(mae_x,model4,width=width, color="red",label="lasso-alpha=0.01") plt.title("lr,sdgr+"+ss+"性能对比图") #将横坐标数值转换为班级 plt.xticks(x + width, classes) #显示柱状图的高度文本 for i in range(len(classes)): plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8) plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8) #plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8) #plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8) #显示图例 plt.legend(loc="upper right") plt.show() #coding=gbk; def plot_line(X,y,model,name): #-------------------------------------------------------------- #z是我们生成的等差数列，用来画出线性模型的图形。 z=np.linspace(0,50,200).reshape(-1,1) plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k') plt.plot(z,z,c="k") plt.xlabel('y') plt.ylabel("y_hat") plt.title(name) plt.show() lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model()models=[lr,sgdr]r2s=[]mess=[]maes=[]nmse=[]results=[]plot_line(X,y,lr,'LinearRegression+'+ss)plot_line(X,y,sgdr,'SGDRegressor+'+ss)#plot_line(X,y,lasso,'lasso'+ss)#plot_line(X,y,ridge,'ridge'+ss)print("sgdr_y_predict")print(sgdr_y_predict)predicts=[lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict]i=0for model in models: result=evaluate(X_test,y_test,predicts[i],model) i=i+1 results.append(result) # r2s.append(result[1]) # mess.append(result[2]) # maes.append(result[3]) # nmse.append(result[0]) #evaluate(X_test,y_test,sgdr_y_predict,sgdr)print(results) #evaluate(X_test,y_test,sgdr_y_predict,sgdr)plot(results[0][1:4],results[1][1:4])

# 从 sklearn.datasets 导入波士顿房价数据读取器。from sklearn.datasets import load_boston# 从读取房价数据存储在变量 boston 中。boston = load_boston()# 输出数据描述。from matplotlib import pyplot as pltfrom matplotlib import font_managerfrom matplotlib import pyplot as pltimport numpy as npimport matplotlib# 参数设置import matplotlib.pyplot as pltplt.rcParams["font.sans-serif"]=["SimHei"] #设置字体plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题# 从sklearn.cross_validation 导入数据分割器。from sklearn.model_selection import train_test_split# 导入 numpy 并重命名为 np。import numpy as npfrom sklearn.linear_model import Ridge, RidgeCVX = boston.dataprint(X.min(axis=0))print(X.max(axis=0))y = boston.target# 随机采样 25% 的数据构建测试样本，其余作为训练样本。X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)# 分析回归目标值的差异。print("The max target value is", np.max(boston.target))print("The min target value is", np.min(boston.target)) print("The average target value is", np.mean(boston.target))# 从 sklearn.preprocessing 导入数据标准化模块。from sklearn.preprocessing import StandardScaler# 分别初始化对特征和目标值的标准化器。ss_X = StandardScaler()ss_y = StandardScaler()# 分别对训练和测试数据的特征以及目标值进行标准化处理。# X_train = ss_X.fit_transform(X_train# X_test = ss_X.transform(X_test)y_train = y_train.reshape(-1, 1)y_test = y_test.reshape(-1, 1)# 从 sklearn.linear_model 导入 LinearRegression。from sklearn.linear_model import LinearRegression# 使用默认配置初始化线性回归器 LinearRegression。def train_model(): lr = LinearRegression() # 使用训练数据进行参数估计。 lr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lr_y_predict = lr.predict(X_test) # 从 sklearn.linear_model 导入 SGDRegressor。 from sklearn.linear_model import SGDRegressor # 使用默认配置初始化线性回归器 SGDRegressor。 sgdr = SGDRegressor() # 使用训练数据进行参数估计。 sgdr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 sgdr_y_predict = sgdr.predict(X_test) ridge = Ridge(alpha=10) # 使用训练数据进行参数估计。 ridge.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 ridge_y_predict = ridge.predict(X_test) return lr,sgdr,ridge,lr_y_predict,sgdr_y_predict,ridge_y_predictdef evaluate(X_test,y_test,lr_y_predict,model):# 使用 LinearRegression 模型自带的评估模块，并输出评估结果。 nmse=model.score(X_test, y_test) print('The value of default measurement of LinearRegression is',nmse ) # 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。 from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error # 使用 r2_score 模块，并输出评估结果。 r2=r2_score(y_test, lr_y_predict) print('The value of R-squared of LinearRegression is',r2 ) # 使用 mean_squared_error 模块，并输出评估结果。 #print(y_test) lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1) #print(lr_y_predict) #print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))) mse=mean_squared_error(y_test, lr_y_predict) print('The mean squared error of LinearRegression is',mse ) # 使用 mean_absolute_error 模块，并输出评估结果。 mae= mean_absolute_error(y_test, lr_y_predict) print('The mean absoluate error of LinearRegression is', mae ) return round(nmse,2),round(r2,2),round(mse,2),round(mae,2) def plot(model1,model2):# 数据 classes = [ 'r2', 'mse', 'mae'] # r2s = [87, 85, 89, 81, 78] # mess = [85, 98, 84, 79, 82] # nmse = [83, 85, 82, 87, 78] # 将横坐标班级先替换为数值 x = np.arange(len(classes)) width = 0.2 r2s_x = x mess_x = x + width nmse_x = x + 2 * width mae_x = x + 3 * width # 绘图 plt.bar(r2s_x, model1, width=width, color='gold', label='LinearRegression') plt.bar(mess_x,model2,width=width,color="silver",label="SGDRegressor") # plt.bar(nmse_x,nmse,width=width, color="saddlebrown",label="mse") # plt.bar(mae_x,maes,width=width, color="red",label="mae") #将横坐标数值转换为班级 plt.xticks(x + width, classes) #显示柱状图的高度文本 for i in range(len(classes)): plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8) plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8) # plt.text(nmse_x[i],nmse[i], nmse[i],va="bottom",ha="center",fontsize=8) # plt.text(mae_x[i],maes[i], maes[i],va="bottom",ha="center",fontsize=8) #显示图例 plt.legend(loc="upper right") plt.show()def plot_line(X,y,model,name): #-------------------------------------------------------------- #z是我们生成的等差数列，用来画出线性模型的图形。 z=np.linspace(0,50,200).reshape(-1,1) plt.scatter(y,model.predict(X),c="orange",edgecolors='k') print(model.predict(X)) plt.plot(z,z,c="k") plt.xlabel('y') plt.ylabel("y_hat") plt.title(name) plt.show()lr,sgdr,ridge,lr_y_predict,sgdr_y_predict,ridge_y_predict=train_model()models=[lr,sgdr,]r2s=[]mess=[]maes=[]nmse=[]results=[] plot_line(X,y,lr,'LinearRegression')plot_line(X,y,sgdr,'SGDRegressor')print("sgdr_y_predict")print(sgdr_y_predict)predicts=[lr_y_predict,sgdr_y_predict]i=0for model in models: result=evaluate(X_test,y_test,predicts[i],model) i=i+1 results.append(result) # r2s.append(result[1]) # mess.append(result[2]) # maes.append(result[3]) # nmse.append(result[0]) #evaluate(X_test,y_test,sgdr_y_predict,sgdr)print(results)plot(results[0][1:4],results[1][1:4] )

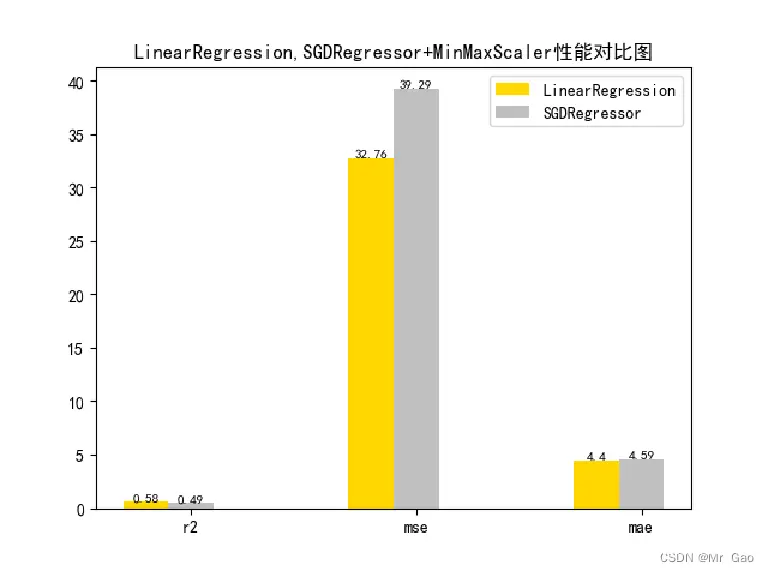
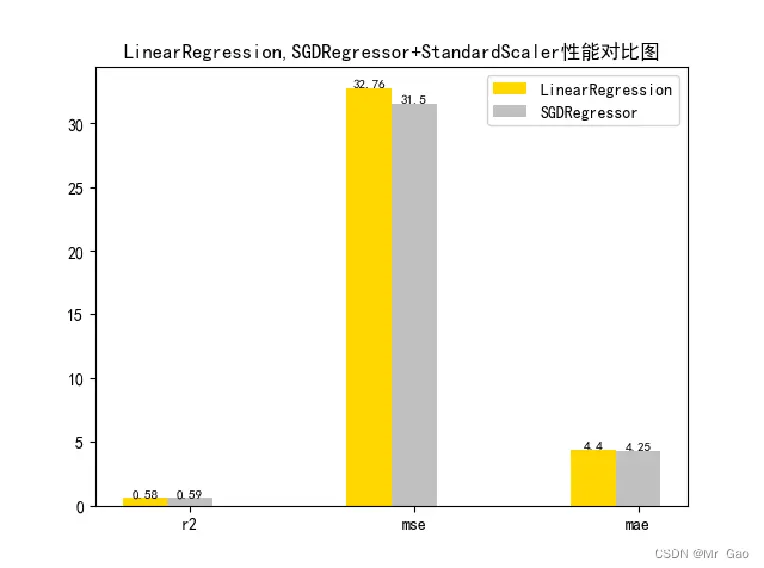
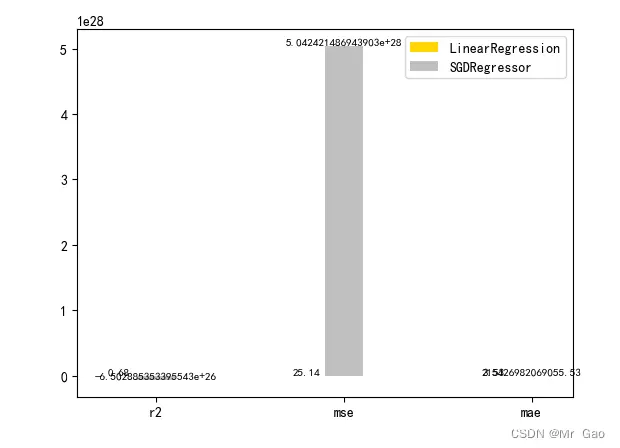
3.3 正则化对比试验

# 从 sklearn.datasets 导入波士顿房价数据读取器。from sklearn.datasets import load_boston# 从读取房价数据存储在变量 boston 中。boston = load_boston()# 输出数据描述。from matplotlib import pyplot as pltfrom matplotlib import font_managerfrom matplotlib import pyplot as pltimport numpy as npimport matplotlib# 参数设置import matplotlib.pyplot as pltplt.rcParams["font.sans-serif"]=["SimHei"] #设置字体plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题# 从sklearn.cross_validation 导入数据分割器。from sklearn.model_selection import train_test_split# 导入 numpy 并重命名为 np。import numpy as npfrom sklearn.linear_model import Ridge,LassoX = boston.datay = boston.target# 随机采样 25% 的数据构建测试样本，其余作为训练样本。X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)# 分析回归目标值的差异。print("The max target value is", np.max(boston.target))print("The min target value is", np.min(boston.target)) print("The average target value is", np.mean(boston.target))# 从 sklearn.preprocessing 导入数据标准化模块。from sklearn.preprocessing import StandardScalerfrom sklearn.preprocessing import MinMaxScalerfrom sklearn.preprocessing import Normalizer# 分别初始化对特征和目标值的标准化器。ss_X = StandardScaler()ss_y = StandardScaler()ss="StandardScaler"# 分别对训练和测试数据的特征以及目标值进行标准化处理。X_train = ss_X.fit_transform(X_train)X_test = ss_X.transform(X_test)y_train = ss_y.fit_transform(y_train.reshape(-1, 1))y_test = ss_y.transform(y_test.reshape(-1, 1))# 从 sklearn.linear_model 导入 LinearRegression。from sklearn.linear_model import LinearRegression# 使用默认配置初始化线性回归器 LinearRegression。def train_model(): lr = LinearRegression() # 使用训练数据进行参数估计。 lr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lr_y_predict = lr.predict(X_test) # 从 sklearn.linear_model 导入 SGDRegressor。 from sklearn.linear_model import SGDRegressor # 使用默认配置初始化线性回归器 SGDRegressor。 sgdr = SGDRegressor() # 使用训练数据进行参数估计。 sgdr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 sgdr_y_predict = sgdr.predict(X_test) ridge = Ridge(alpha=10) # 使用训练数据进行参数估计。 ridge.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 ridge_y_predict = ridge.predict(X_test) # Lasso lasso = Lasso(alpha=0.01) # 使用训练数据进行参数估计。 lasso.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lasso_y_predict = lasso.predict(X_test) return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict def evaluate(X_test,y_test,lr_y_predict,model):# 使用 LinearRegression 模型自带的评估模块，并输出评估结果。 nmse=model.score(X_test, y_test) print('The value of default measurement of LinearRegression is',nmse ) # 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。 from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error # 使用 r2_score 模块，并输出评估结果。 r2=r2_score(y_test, lr_y_predict) print('The value of R-squared of LinearRegression is',r2 ) # 使用 mean_squared_error 模块，并输出评估结果。 #print(y_test) lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1) #print(lr_y_predict) #print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))) mse=mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean squared error of LinearRegression is',mse ) # 使用 mean_absolute_error 模块，并输出评估结果。 mae= mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean absoluate error of LinearRegression is', mae ) return round(nmse,2),round(r2,2),round(mse,2),round(mae,2) def plot(model1,model2,model3,model4):# 数据 classes = [ 'r2', 'mse', 'mae'] # r2s = [87, 85, 89, 81, 78] # mess = [85, 98, 84, 79, 82] # nmse = [83, 85, 82, 87, 78] # 将横坐标班级先替换为数值 x = np.arange(len(classes)) width = 0.2 r2s_x = x mess_x = x + width nmse_x = x + 2 * width mae_x = x + 3 * width # 绘图 plt.bar(r2s_x, model1, width=width, color='gold', label='LinearRegression') plt.bar(mess_x,model2,width=width,color="silver",label="SGDRegressor") plt.bar(nmse_x,model3,width=width, color="saddlebrown",label="ridge-alpha=10") plt.bar(mae_x,model4,width=width, color="red",label="lasso-alpha=0.01") plt.title("lr,sdgr,lasso,ridge+"+ss+"性能对比图") #将横坐标数值转换为班级 plt.xticks(x + width, classes) #显示柱状图的高度文本 for i in range(len(classes)): plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8) plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8) plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8) plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8) #显示图例 plt.legend(loc="upper right") plt.show() #coding=gbk; def plot_line(X,y,model,name): z=np.linspace(0,50,200).reshape(-1,1) plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k') plt.plot(z,z,c="k") plt.xlabel('y') plt.ylabel("y_hat") plt.title(name) plt.show() lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model()models=[lr,sgdr,ridge,lasso]r2s=[]mess=[]maes=[]nmse=[]results=[]plot_line(X,y,lr,'LinearRegression+'+ss)plot_line(X,y,sgdr,'SGDRegressor'+ss)plot_line(X,y,lasso,'lasso'+ss)plot_line(X,y,ridge,'ridge'+ss)print("sgdr_y_predict")print(sgdr_y_predict)predicts=[lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict]i=0for model in models: result=evaluate(X_test,y_test,predicts[i],model) i=i+1 results.append(result) # r2s.append(result[1]) # mess.append(result[2]) # maes.append(result[3]) # nmse.append(result[0]) #evaluate(X_test,y_test,sgdr_y_predict,sgdr)print(results) #evaluate(X_test,y_test,sgdr_y_predict,sgdr)plot(results[0][1:4],results[1][1:4],results[2][1:4],results[3][1:4])

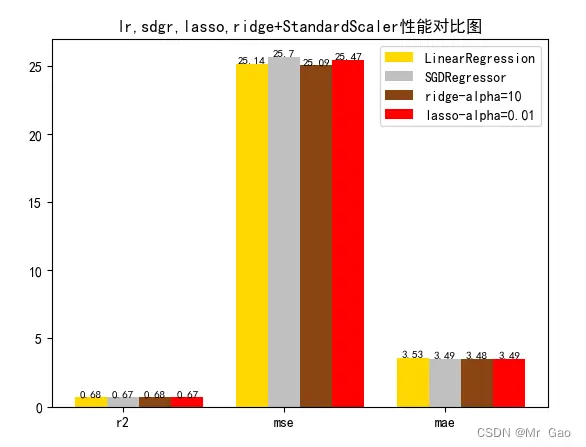
3.4多项式回归degree对比实验

# 从 sklearn.datasets 导入波士顿房价数据读取器。from sklearn.datasets import load_boston# 从读取房价数据存储在变量 boston 中。boston = load_boston()# 输出数据描述。from matplotlib import pyplot as pltfrom matplotlib import font_managerfrom matplotlib import pyplot as pltimport numpy as npimport matplotlib# 参数设置from sklearn.preprocessing import PolynomialFeaturesimport matplotlib.pyplot as pltplt.rcParams["font.sans-serif"]=["SimHei"] #设置字体plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题# 从sklearn.cross_validation 导入数据分割器。from sklearn.model_selection import train_test_split# 导入 numpy 并重命名为 np。import numpy as npfrom sklearn.linear_model import Ridge,LassoX = boston.datay = boston.target# 随机采样 25% 的数据构建测试样本，其余作为训练样本。X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)# 分析回归目标值的差异。print("The max target value is", np.max(boston.target))print("The min target value is", np.min(boston.target)) print("The average target value is", np.mean(boston.target))# 从 sklearn.preprocessing 导入数据标准化模块。from sklearn.preprocessing import StandardScalerfrom sklearn.preprocessing import MinMaxScalerfrom sklearn.preprocessing import Normalizer# 分别初始化对特征和目标值的标准化器。ss_X = StandardScaler()ss_y = StandardScaler()ss="StandardScaler"# 分别对训练和测试数据的特征以及目标值进行标准化处理。X_train = ss_X.fit_transform(X_train)X_test = ss_X.transform(X_test)y_train[0]=y_train[0]+300y_train = ss_y.fit_transform(y_train.reshape(-1, 1))y_test = ss_y.transform(y_test.reshape(-1, 1))# 从 sklearn.linear_model 导入 LinearRegression。from sklearn.linear_model import LinearRegression# 使用默认配置初始化线性回归器 LinearRegression。def train_model(): poly_reg = PolynomialFeatures(degree=1) # 数据转换 x0-->1 x1-->x x2-->x^2 x3-->x^3 x_poly = poly_reg.fit_transform(X_train) # 建模 #lin_reg = LinearRegression().fit(x_poly, y_data) lr = LinearRegression().fit(x_poly, y_train[:,0]) # 使用训练数据进行参数估计。 lr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lr_y_predict = lr.predict(X_test) # 从 sklearn.linear_model 导入 SGDRegressor。 from sklearn.linear_model import SGDRegressor # 使用默认配置初始化线性回归器 SGDRegressor。 poly_reg = PolynomialFeatures(degree=2) # 数据转换 x0-->1 x1-->x x2-->x^2 x3-->x^3 x_poly = poly_reg.fit_transform(X_train) sgdr = LinearRegression().fit(x_poly, y_train[:,0]) # 使用训练数据进行参数估计。 sgdr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 sgdr_y_predict = sgdr.predict(X_test) poly_reg = PolynomialFeatures(degree=3) # 数据转换 x0-->1 x1-->x x2-->x^2 x3-->x^3 x_poly = poly_reg.fit_transform(X_train) ridge = LinearRegression().fit(x_poly, y_train[:,0]) # 使用训练数据进行参数估计。 ridge.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 ridge_y_predict = ridge.predict(X_test) # Lasso poly_reg = PolynomialFeatures(degree=4) # 数据转换 x0-->1 x1-->x x2-->x^2 x3-->x^3 x_poly = poly_reg.fit_transform(X_train) lasso = LinearRegression().fit(x_poly, y_train[:,0]) # 使用训练数据进行参数估计。 lasso.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lasso_y_predict = lasso.predict(X_test) return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict def evaluate(X_test,y_test,lr_y_predict,model):# 使用 LinearRegression 模型自带的评估模块，并输出评估结果。 nmse=model.score(X_test, y_test) print('The value of default measurement of LinearRegression is',nmse ) # 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。 from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error # 使用 r2_score 模块，并输出评估结果。 r2=r2_score(y_test, lr_y_predict) print('The value of R-squared of LinearRegression is',r2 ) # 使用 mean_squared_error 模块，并输出评估结果。 #print(y_test) lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1) #print(lr_y_predict) #print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))) mse=mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean squared error of LinearRegression is',mse ) # 使用 mean_absolute_error 模块，并输出评估结果。 mae= mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean absoluate error of LinearRegression is', mae ) return round(nmse,2),round(r2,2),round(mse,2),round(mae,2) def plot(model1,model2,model3,model4):# 数据 classes = [ 'r2', 'mse', 'mae'] # r2s = [87, 85, 89, 81, 78] # mess = [85, 98, 84, 79, 82] # nmse = [83, 85, 82, 87, 78] # 将横坐标班级先替换为数值 x = np.arange(len(classes)) width = 0.2 r2s_x = x mess_x = x + width nmse_x = x + 2 * width mae_x = x + 3 * width # 绘图 plt.bar(r2s_x, model1, width=width, color='gold', label='ploy-degree=1') plt.bar(mess_x,model2,width=width,color="silver",label="ploy-degree=2") plt.bar(nmse_x,model3,width=width, color="saddlebrown",label="ploy-degree=3") plt.bar(mae_x,model4,width=width, color="red",label="ploy-degree=4") plt.title("不同degree多项式回归+"+ss+"性能对比图") #将横坐标数值转换为班级 plt.xticks(x + width, classes) #显示柱状图的高度文本 for i in range(len(classes)): plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8) plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8) plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8) plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8) #显示图例 plt.legend(loc="upper right") plt.show() #coding=gbk; def plot_line(X,y,model,name): #-------------------------------------------------------------- #z是我们生成的等差数列，用来画出线性模型的图形。 z=np.linspace(0,50,200).reshape(-1,1) plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k') plt.plot(z,z,c="k") plt.xlabel('y') plt.ylabel("y_hat") plt.title(name) plt.show() lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model()models=[lr,sgdr,ridge,lasso]r2s=[]mess=[]maes=[]nmse=[]results=[]#plot_line(X,y,lr,'LinearRegression+'+ss)#plot_line(X,y,sgdr,'SGDRegressor'+ss)#plot_line(X,y,lasso,'lasso'+ss)#plot_line(X,y,ridge,'ridge'+ss)print("sgdr_y_predict")print(sgdr_y_predict)predicts=[lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict]i=0for model in models: result=evaluate(X_test,y_test,predicts[i],model) i=i+1 results.append(result) # r2s.append(result[1]) # mess.append(result[2]) # maes.append(result[3]) # nmse.append(result[0]) #evaluate(X_test,y_test,sgdr_y_predict,sgdr)print(results) #evaluate(X_test,y_test,sgdr_y_predict,sgdr)plot(results[0][1:4],results[1][1:4],results[2][1:4],results[3][1:4])

截图：

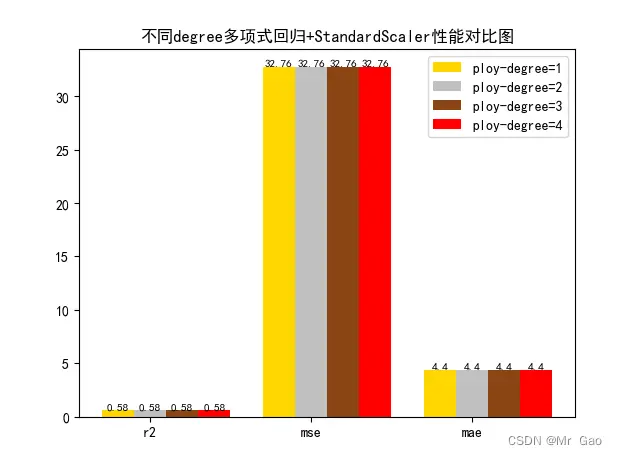
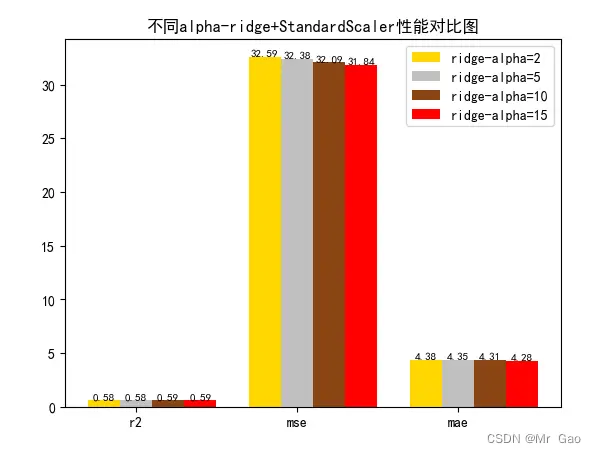
3.5 岭回归alpha敏感度实验

# 从 sklearn.datasets 导入波士顿房价数据读取器。from sklearn.datasets import load_boston# 从读取房价数据存储在变量 boston 中。boston = load_boston()# 输出数据描述。from matplotlib import pyplot as pltfrom matplotlib import font_managerfrom matplotlib import pyplot as pltimport numpy as npimport matplotlib# 参数设置import matplotlib.pyplot as pltplt.rcParams["font.sans-serif"]=["SimHei"] #设置字体plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题# 从sklearn.cross_validation 导入数据分割器。from sklearn.model_selection import train_test_split# 导入 numpy 并重命名为 np。import numpy as npfrom sklearn.linear_model import Ridge,LassoX = boston.datay = boston.target# 随机采样 25% 的数据构建测试样本，其余作为训练样本。X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)# 分析回归目标值的差异。print("The max target value is", np.max(boston.target))print("The min target value is", np.min(boston.target)) print("The average target value is", np.mean(boston.target))# 从 sklearn.preprocessing 导入数据标准化模块。from sklearn.preprocessing import StandardScalerfrom sklearn.preprocessing import MinMaxScalerfrom sklearn.preprocessing import Normalizer# 分别初始化对特征和目标值的标准化器。ss_X = StandardScaler()ss_y = StandardScaler()ss="StandardScaler"# 分别对训练和测试数据的特征以及目标值进行标准化处理。X_train = ss_X.fit_transform(X_train)X_test = ss_X.transform(X_test)y_train[0]=y_train[0]+300y_train = ss_y.fit_transform(y_train.reshape(-1, 1))y_test = ss_y.transform(y_test.reshape(-1, 1))# 从 sklearn.linear_model 导入 LinearRegression。from sklearn.linear_model import LinearRegression# 使用默认配置初始化线性回归器 LinearRegression。def train_model(): lr = Ridge(alpha=2) # 使用训练数据进行参数估计。 lr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lr_y_predict = lr.predict(X_test) # 从 sklearn.linear_model 导入 SGDRegressor。 from sklearn.linear_model import SGDRegressor # 使用默认配置初始化线性回归器 SGDRegressor。 sgdr = Ridge(alpha=5) # 使用训练数据进行参数估计。 sgdr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 sgdr_y_predict = sgdr.predict(X_test) ridge = Ridge(alpha=10) # 使用训练数据进行参数估计。 ridge.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 ridge_y_predict = ridge.predict(X_test) # Lasso lasso =Ridge(alpha=15) # 使用训练数据进行参数估计。 lasso.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lasso_y_predict = lasso.predict(X_test) return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict def evaluate(X_test,y_test,lr_y_predict,model):# 使用 LinearRegression 模型自带的评估模块，并输出评估结果。 nmse=model.score(X_test, y_test) print('The value of default measurement of LinearRegression is',nmse ) # 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。 from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error # 使用 r2_score 模块，并输出评估结果。 r2=r2_score(y_test, lr_y_predict) print('The value of R-squared of LinearRegression is',r2 ) # 使用 mean_squared_error 模块，并输出评估结果。 #print(y_test) lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1) #print(lr_y_predict) #print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))) mse=mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean squared error of LinearRegression is',mse ) # 使用 mean_absolute_error 模块，并输出评估结果。 mae= mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean absoluate error of LinearRegression is', mae ) return round(nmse,2),round(r2,2),round(mse,2),round(mae,2) def plot(model1,model2,model3,model4):# 数据 classes = [ 'r2', 'mse', 'mae'] # r2s = [87, 85, 89, 81, 78] # mess = [85, 98, 84, 79, 82] # nmse = [83, 85, 82, 87, 78] # 将横坐标班级先替换为数值 x = np.arange(len(classes)) width = 0.2 r2s_x = x mess_x = x + width nmse_x = x + 2 * width mae_x = x + 3 * width # 绘图 plt.bar(r2s_x, model1, width=width, color='gold', label='ridge-alpha=2') plt.bar(mess_x,model2,width=width,color="silver",label="ridge-alpha=5") plt.bar(nmse_x,model3,width=width, color="saddlebrown",label="ridge-alpha=10") plt.bar(mae_x,model4,width=width, color="red",label="ridge-alpha=15") plt.title("不同alpha-ridge+"+ss+"性能对比图") #将横坐标数值转换为班级 plt.xticks(x + width, classes) #显示柱状图的高度文本 for i in range(len(classes)): plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8) plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8) plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8) plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8) #显示图例 plt.legend(loc="upper right") plt.show() #coding=gbk; def plot_line(X,y,model,name): #-------------------------------------------------------------- #z是我们生成的等差数列，用来画出线性模型的图形。 z=np.linspace(0,50,200).reshape(-1,1) plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k') plt.plot(z,z,c="k") plt.xlabel('y') plt.ylabel("y_hat") plt.title(name) plt.show() lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model()models=[lr,sgdr,ridge,lasso]r2s=[]mess=[]maes=[]nmse=[]results=[]plot_line(X,y,lr,'LinearRegression+'+ss)plot_line(X,y,sgdr,'SGDRegressor'+ss)plot_line(X,y,lasso,'lasso'+ss)plot_line(X,y,ridge,'ridge'+ss)print("sgdr_y_predict")print(sgdr_y_predict)predicts=[lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict]i=0for model in models: result=evaluate(X_test,y_test,predicts[i],model) i=i+1 results.append(result) # r2s.append(result[1]) # mess.append(result[2]) # maes.append(result[3]) # nmse.append(result[0]) #evaluate(X_test,y_test,sgdr_y_predict,sgdr)print(results) #evaluate(X_test,y_test,sgdr_y_predict,sgdr)plot(results[0][1:4],results[1][1:4],results[2][1:4],results[3][1:4])

运行结果：