目录

一、SVC理解进阶

1. C（硬间隔与软间隔）

2. class_weight

二、模型评估指标（SVC）

1. 混淆矩阵 （Confusion Matrix）

（1）准确率 —— 模型整体效果

（2）精确度 —— 捕捉少数类

（3）召回率（Recall）—— 捕捉少数类

（4）F1 score—— 捕捉少数类

（5）假负率

（6）特异度 —— 判错多数类的考量

（7）假正率（FPR）—— 判错多数类的考量

三、sklearn中的混淆矩阵

四、ROC曲线和AUC面积

1. 曲线理解

2. sklearn 实现

---

一、SVC理解进阶

1. C（硬间隔与软间隔）

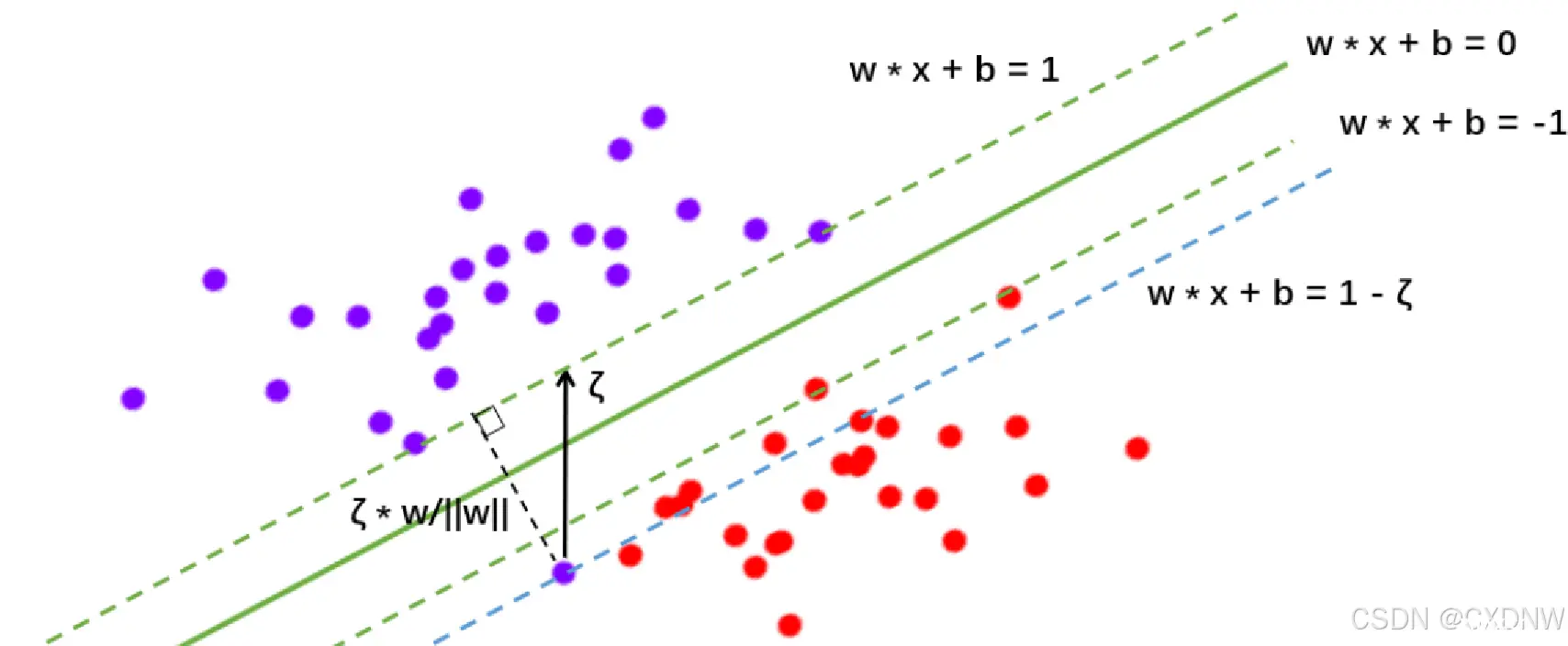
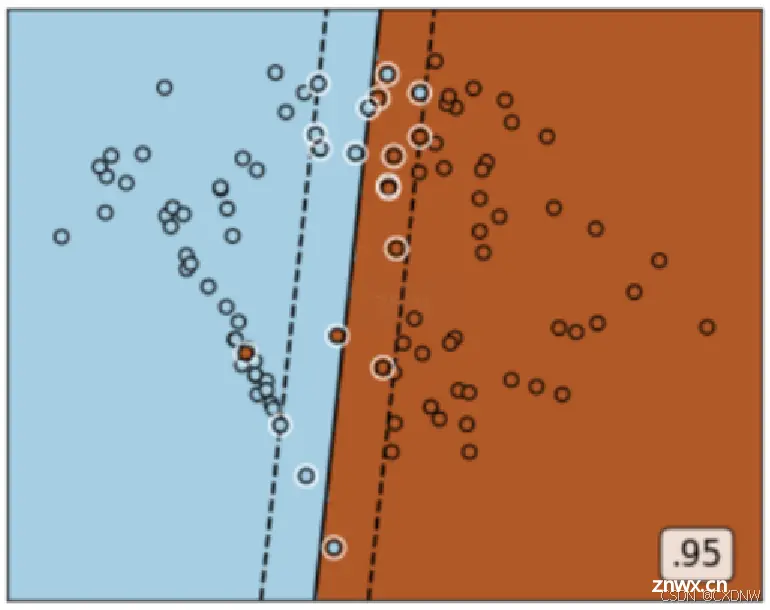
        有一些数据，可能是 线性可分，但 在 线性可分状况下 训练准确率 不能达到 100%，即 无法让训练误差为 0，这样的数据被称为 “存在软间隔的数据” 。此时 需要 让决策边界能够 忍受一小部分训练误差，就 不能单纯地寻 求最大边际了。

        虚线超平面

是 由 混杂在红色点中间的 紫色点来决定的，所以 此时，这个 紫色点就是 支持向量。所以 软间隔 让决定 两条虚线超平面的 支持向量 可能是 来自于同一个类别的 样本点，而 硬间隔的时候 两条虚线超平面 必须是由 来自两个不同类别的 支持向量决定的。

        c 值会决定我们 究竟是 依赖红色点 作为支持向量（只追求最大边界），还是要 依赖软间隔中，混杂 在红色点中的 紫色点来 作为支持向量（追求最大边界和判断正确的平衡）。

        如果 C 值 设定比较大，那 SVC 可能会选择 边际较小的，能够 更好地分类 所有训练点的 决策边界，不过 模型的训练时间 也会更长。如果 C 的 设定值 较小，那 SVC 会尽量 最大化边界，尽量 将掉落在决策边界 另一方的样本点 预测正确，决策 功能会更简单，但 代价是训练的 准确度，因为此时会 有更多红色的点被 分类错误。换句话说，C 在 SVM中的影响就像 正则化参数对逻辑回归的 影响。

2. class_weight

        对于分类问题，永远都逃不过的一个 痛点就是 样本不均衡问题。样本不均衡 是 指在一组数据集中，标签的 一类天生占有 很大的比例，但 我们有着 捕捉出 某种特定的分类的 需求的状况。

        样本不均衡的情况下，分类模型 天生会倾向于 多数的类，让多数类 更容易被判断正确，少数类 被牺牲掉。因为 对于模型而言，样本量 越大的标签 可以学习的 信息越多，算法 就会 更加依赖于从多数类中 学到的信息来 进行判断。如果 希望捕获少数类，模型 就会失败。

        其次，模型评估指标 会失去意义。这种分类状况下，即便 模型 什么也不做，把 所有标签 都判断为 多数类，准确率 也能非常高，这使得 模型评估指标 accuracy 变得毫无意义，根本 无法达到 特定分类的 建模目的。

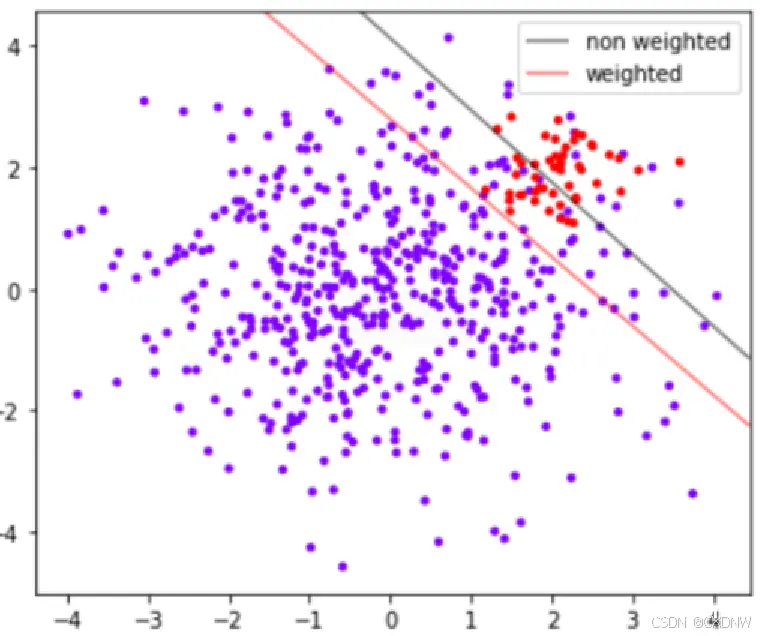
        支持向量机中地决策仅仅 受决策边界的影响，而 决策边界 又受到 参数 C 和 支持向量的 影响。在支持向量机中，要 大力依赖 调节样本均衡的参数：SVC 类中的 class_weight 和 接口 fit 中可以设定的 sample_weight。

二、模型评估指标（SVC）

        单纯地追求 捕捉出少数类，就会 成本太高，而不顾及少数类，又会无法达成 模型的效果。所以在现实中，往往 在寻找捕获少数类的能力 和 将多数类判错后需要 付出的成本的 平衡。如果一个 模型在 能够尽量捕获 少数类的情况 下，还 能够尽量 对多数类 判断正确，则 这个模型 就非常优秀了。为了 评估这样的 能力，将 引入新的 模型评估指标：混淆矩阵和ROC曲线。

1. 混淆矩阵 （Confusion Matrix）

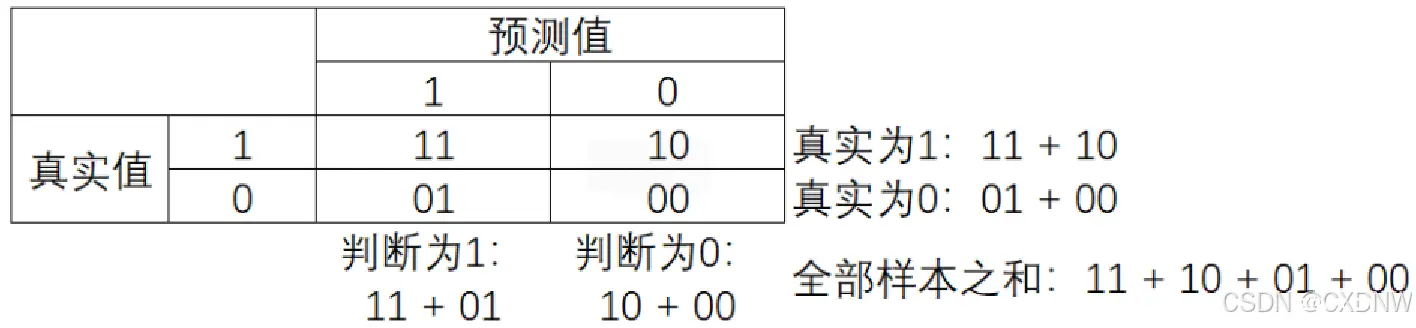
        混淆矩阵是 二分类问题的 多维衡量指标 体系，在 样本不平衡时 极其有用。在 混淆矩阵中，将 少数类认为 是正例，多数类认为 是负例。在 SVM 里，少数类 为 1，多数类为 -1。普通的混淆矩阵，一般使用｛0,1｝来表示。

        混淆矩阵中，永远是真实值 在前，预测值 在后。11 和 00 的 对角线就是 全部预测正确的， 01 和 10 的对角线 就是全部 预测错误的。基于 混淆短阵，有 六个不同的模型评估指标，这些 评估指标的 范围都在 [0, 1] 之间，所有以 11 和 00 为分子的指标 都是越接近 1 越好，所有以 01 和 10 为 分子的 指标都是 越接近 0 越好。

        对于所有的指标，用 橙色表示分母，用 绿色表示 分子，则有：

（1）准确率——模型整体效果

        准确率 Accuracy 就是 所有 预测 正确的 所有样本 除以总样本，通常来说 越接近 1 越好。

（2）精确度——捕捉少数类

        精确度 Precision，又叫 查准率，表示 所有 被预测为是 少数类的 样本中，真正的 少数类所占的 比例。精确度是 “ 将多数类判错后所需付出成本 〞的衡量。

        在支持向量机中，精确度 可以 被形象地表示为 决策边界 上方的所有点 中，红色点 所占的 比例。精确度越高，代表捕捉正确的红色点越多，对 少数类的预测 越精确。精确度 越低，则 代表我们 误伤了过多的多数类。

        当每一次将 多数类判断错误的 成本非常 高昂的时候，我们会 追求高精确度。精确度 越低，对多数类的 判断就会 越错误。当然，如果 目标是 不计一切代价 捕获少数类，那并不在意 精确度。

（3）召回率（Recall）——捕捉少数类

        召回率 Recall，又被称为 敏感度（sensitivity），真正率，查全率。表示 所有真实为 1 的样本中，被 预测正确的样本 所占的比例。

        在支持向量机中，召回率 可以被表示为 决策边界上方的 所有红色点 占全部样本中 的 红色点的比例。召回率 越高，代表 尽量捕捉出 了越多的 少数类，召回率 越低，代表我们 没有捕捉出足够的少数类。

        召回率 和 精确度是 此消彼长的，两者之间的 平衡代表了 捕捉少数类的 需求 和 尽量 不要误伤多数类的 需求的 平衡。如果 希望 不计一切 代价 找出少数类，那就会 追求 高召回率，相反如果 目标 不是尽量 捕获少数类，那就 不需要在意 召回率。

（4）F1 score——捕捉少数类

        同时 兼顾 精确度 和 召回率两者的 调和平均数 作为 考量两者 平衡的综合性指标，称之为 F1 measure。两个数之间的 调和平均倾向于 靠近两个数中 比较小的那一个数，因此 追求尽量高的F1 measure，能够 保证 精确度 和 召回率 都比较高。F1 measure在 [0 ,1] 之间分布，越接近 1 越好。

（5）假负率

        假负率（False Negative Rate），它等于 1 - Recall，用于 衡量 所有真实为 1 的样本中，被错误 判断为 0 的。通常用得不多。

（6）特异度——判错多数类的考量

​​​​​​​

        特异度（Specificity）表示 所有真实为 0 的样本 中，被 正确预测为 0 的样本 所占的比例。在支持向量机中，可以 形象地表示为 决策边界下方的 点占所 有紫色点的 比例。特异度 衡量了一个模型将多数 类判断正确的 能力。

（7）假正率（FPR）——判错多数类的考量

​​​​​​​

        1-specificity 是一个 模型将多数类 判断错误的能力，这种 能力被叫做 假正率 （False Positive Rate）。

        在支持向量机中，假正率 就是决策边界上方的 紫色点（所有被判断错误的多数类）占所有紫色点的比例。当样本均 衡过后，假正率 会 更高，因为 有更多紫色点被判断错误，而 样本均衡 之前，假正率 比较低，被 判错的紫色点 比较少。所以 假正率其实类似于 Precision的 反向指标，Precision 衡量 有多少少数点 被判断正确，而假正率 FPR 衡量有多少多数 点 被判断错误，性质 是十分类似的。

三、sklearn中的混淆矩阵

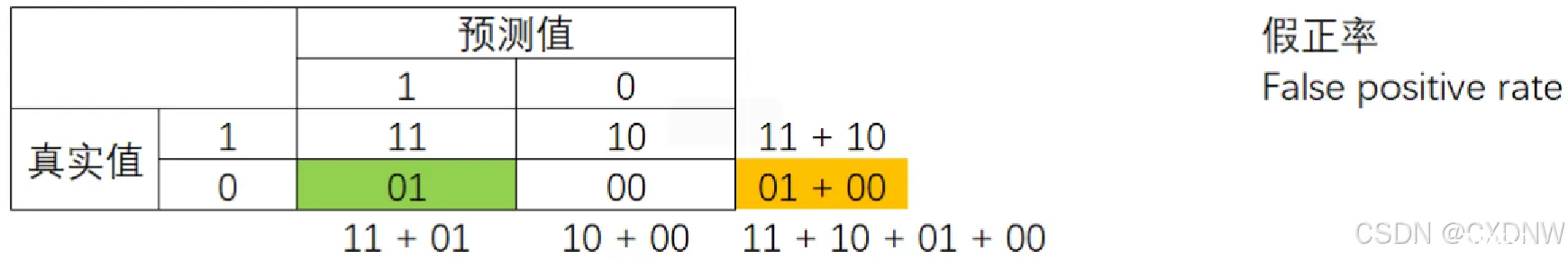
四、ROC曲线和AUC面积

1. 曲线理解

        建立 ROC 曲线的 根本目的是 找寻 Recall 和 FPR 之间的 平衡，让我们 能够衡量模型 在尽量捕捉少数类的 时候，误伤 多数类的情况 会如何变化。横坐标是 FPR，代表着 模型将多数类判断错误的 能力，纵坐标 Recall，代表着模型捕捉少数类的 能力，所以 ROC 曲线 代表着，随着Recall 的 不断增加，FPR 如何增加。

        我们希望随着 Recall 的不断提升，FPR 增加得 越慢越好，这说明我们 可以尽量 高效地捕捉出少数类，而不会 将很多地 多数类 判断错误。所以，我们 希望看到的 图像是，纵坐标急速上升，横坐标 缓慢增长，也就是 在整个图像 左上方的 一条弧线。这代表 模型的 效果很不错，拥有较好的 捕获少数类的能力。

        中间的 虚线代表着，当 recall 增加 1%，我们的 FPR 也增加 1%，也就是说，每 捕捉出 一个少数 类，就会 有一个 多数类 被判错，这种情况下，模型的效果就不好，这种 模型捕获 少数类的结果，会让许多多数类 被误伤，从而增加成本。

        ROC曲线通常都是 凸型的。对于一条凸型 ROC 曲线来说，曲线 越靠近 左上角越好，越往下越糟糕，曲线如果 在虚线的下方，则证明模型完全无法使用。对于一条 凹型 ROC 曲线来说，应该越 靠近 右下角越好，凹形曲线 代表模型的 预测结果 与 真实情况 完全相反，那也 不算 非常糟糕，只要 手动将模型的 结果逆转，就 可以得到 一条左上方的 弧线了。最 糟糕的就是，无论 曲线是 凹形 还是 凸型，曲线 位于图像 中间，和虚线 非常靠近，那我们 拿它无能为力。

2. sklearn 实现

<code># 计算ROC曲线的横坐标假正率FPR、纵坐标Recall和对应的阈值的类：

sklearn.metrics.roc_curve(y_true, y_score, pos_label=None, sample_weight=None, drop_ intermediate= True）

"""

y_true：数组，形状=[n_samples]，真实标签。

y_score：数组，形状=[n_samples]，置信度分数，可以是正类样本的概率值，或置信度分数，或者decision_function返回的距离。

pos_label：整数或者字符串，默认None，表示被认为是正类样本的类别。

sample_weight：形如 [n_samples]的类数组结构，可不填，表示样本的权重。

drop_intermediate：布尔值，默认True，如果设置为True，表示会舍弃一些。ROC曲线上不显示的阈值点，这对于计算一个比较轻量的ROC曲线来说非常有用。

return：FPR，Recall、阈值。

"""

# 计算AUC面积：

sklearn.metrics.roc_auc_score(y_true, y_score, average=‘macro’, sample_weight=None, max_fpr=None）

补充：利用 ROC 曲线找出最佳阈值

        ROC 曲线 反应的是 recall 增加的时候 FPR 如何变化，也就是 当模型捕获 少数类的 能力变强的 时候，会误 伤多数类的情况 是否严重。我们的 希望模型 在捕获 少数类的 能力变强的 时候，尽量 不误伤多数类，也就是说，随着 recall 的变大，FPR 的大小 越小 越好。所以 我们希望 找到的 阈值点，其实是 Recall 和 FPR 差距 最大的点。这个点，又叫做 约登指数。其实这个点就是图像上离左上角最近的点，离 中间虚线 最远的点，也是ROC曲线的转折点。