支持向量机回归预测(SVR)的MATLAB实现(含源代码)
沅_Yuan 2024-07-07 10:35:01 阅读 57
支持向量机(Support Vector Machine, SVM)是一种常用于分类和回归分析的机器学习算法。虽然SVM最为人熟知的是其分类应用,但它同样适用于回归任务,被称为支持向量回归(Support Vector Regression, SVR)。以下是SVR的详细介绍:
支持向量回归的基本概念
SVR的目标是找到一个函数,该函数与大多数训练数据点偏差不超过一个给定的阈值(即“ε”)。在SVM分类中,模型试图找到一个能够最好地分开两类数据的超平面,而在SVR中,模型试图找到一个能够最精确预测目标值的函数。
主要步骤
定义损失函数:
SVR使用一种ε-不敏感损失函数(ε-insensitive loss function),其定义为:

该函数的目的是使偏差在ε范围内的预测不被视为错误,从而允许模型忽略一些小的偏差。
找到最优平面:
在SVR中,模型试图找到一个能够最小化ε-不敏感损失函数的回归平面,同时确保所有数据点尽可能接近该平面。
正则化参数:
SVR中引入了正则化参数C以控制模型的复杂度。正则化参数决定了我们允许有多少点超出ε范围。较大的C值允许更多的点超出ε范围,从而可能会导致过拟合;较小的C值则会使模型更简单,可能会欠拟合。
数学公式
SVR的目标是通过优化以下公式来找到回归函数:

在满足以下约束条件下:

核函数
与SVM分类类似,SVR也可以使用核函数来处理非线性数据。常用的核函数包括:
线性核函数
多项式核函数
径向基函数(RBF)
Sigmoid核函数
核函数的使用使得SVR可以在高维空间中找到最优的回归平面,从而处理复杂的非线性关系。
应用场景
SVR被广泛应用于以下场景:
金融市场预测:如股票价格预测、市场趋势分析等。
工业过程控制:如生产过程参数的预测和控制。
生物信息学:如基因表达数据分析、药物活性预测等。
经济学:如GDP、CPI等经济指标的预测。
优缺点
优点:
能够处理高维数据,并且在样本数量较少的情况下表现良好。
灵活的核函数使其能够处理非线性数据。
缺点:
对参数(如C和ε)的选择敏感,通常需要通过交叉验证来选择最佳参数。
训练时间较长,特别是对于大规模数据集。
综上所述,SVR是一种强大的回归分析工具,适用于各种复杂的回归任务,尤其是在高维和非线性数据的处理上表现突出。
MATLAB完整源代码:
<code>%% 清空环境变量
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行
%% 导入数据
res = xlsread('数据集.xlsx');
%% 数据分析
num_size = 0.7; % 训练集占数据集比例
outdim = 1; % 最后一列为输出
num_samples = size(res, 1); % 样本个数
%res = res(randperm(num_samples), :); % 打乱数据集(不希望打乱时,注释该行)
num_train_s = ceil(num_size * num_samples)+1; % 训练集样本个数
f_ = size(res, 2) - outdim; % 输入特征维度
%% 划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);
P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);
%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);
[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%% 转置以适应模型
p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';
%% 创建模型
c = 4.0; % 惩罚因子
g = 0.8; % 径向基函数参数
cmd = [' -t 2',' -c ',num2str(c),' -g ',num2str(g),' -s 3 -p 0.01'];
model = svmtrain(t_train, p_train, cmd);
%% 仿真预测
[t_sim1, error_1] = svmpredict(t_train, p_train, model);
[t_sim2, error_2] = svmpredict(t_test , p_test , model);
%% 数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);
%% 均方根误差
error1 = sqrt(sum((T_sim1' - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2' - T_test ).^2) ./ N);
%% 绘图
figure
plot(1: M, T_train, 'r-*', 1: M, T_sim1, 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = { '训练集预测结果对比'; ['RMSE=' num2str(error1)]};
title(string)
xlim([1, M])
grid
figure
plot(1: N, T_test, 'r-*', 1: N, T_sim2, 'b-o', 'LineWidth', 1)code>
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = { '测试集预测结果对比'; ['RMSE=' num2str(error2)]};
title(string)
xlim([1, N])
grid
%% 相关指标计算
% R2
R1 = 1 - norm(T_train - T_sim1')^2 / norm(T_train - mean(T_train))^2;code>
R2 = 1 - norm(T_test - T_sim2')^2 / norm(T_test - mean(T_test ))^2;
disp(['训练集数据的R2为:', num2str(R1)])
disp(['测试集数据的R2为:', num2str(R2)])
% MAE
mae1 = sum(abs(T_sim1' - T_train)) ./ M ;
mae2 = sum(abs(T_sim2' - T_test )) ./ N ;
disp(['训练集数据的MAE为:', num2str(mae1)])
disp(['测试集数据的MAE为:', num2str(mae2)])
% MBE
mbe1 = sum(T_sim1' - T_train) ./ M ;
mbe2 = sum(T_sim2' - T_test ) ./ N ;
disp(['训练集数据的MBE为:', num2str(mbe1)])
disp(['测试集数据的MBE为:', num2str(mbe2)])
%% 绘制散点图
sz = 25;
c = 'b';
figure
scatter(T_train, T_sim1, sz, c)
hold on
plot(xlim, ylim, '--k')
xlabel('训练集真实值');
ylabel('训练集预测值');
xlim([min(T_train) max(T_train)])
ylim([min(T_sim1) max(T_sim1)])
title('训练集预测值 vs. 训练集真实值')
figure
scatter(T_test, T_sim2, sz, c)
hold on
plot(xlim, ylim, '--k')
xlabel('测试集真实值');
ylabel('测试集预测值');
xlim([min(T_test) max(T_test)])
ylim([min(T_sim2) max(T_sim2)])
title('测试集预测值 vs. 测试集真实值')
**
提示:代码还缺少数据集和相关文件,再文章底部可以免费下载
**
运行效果:
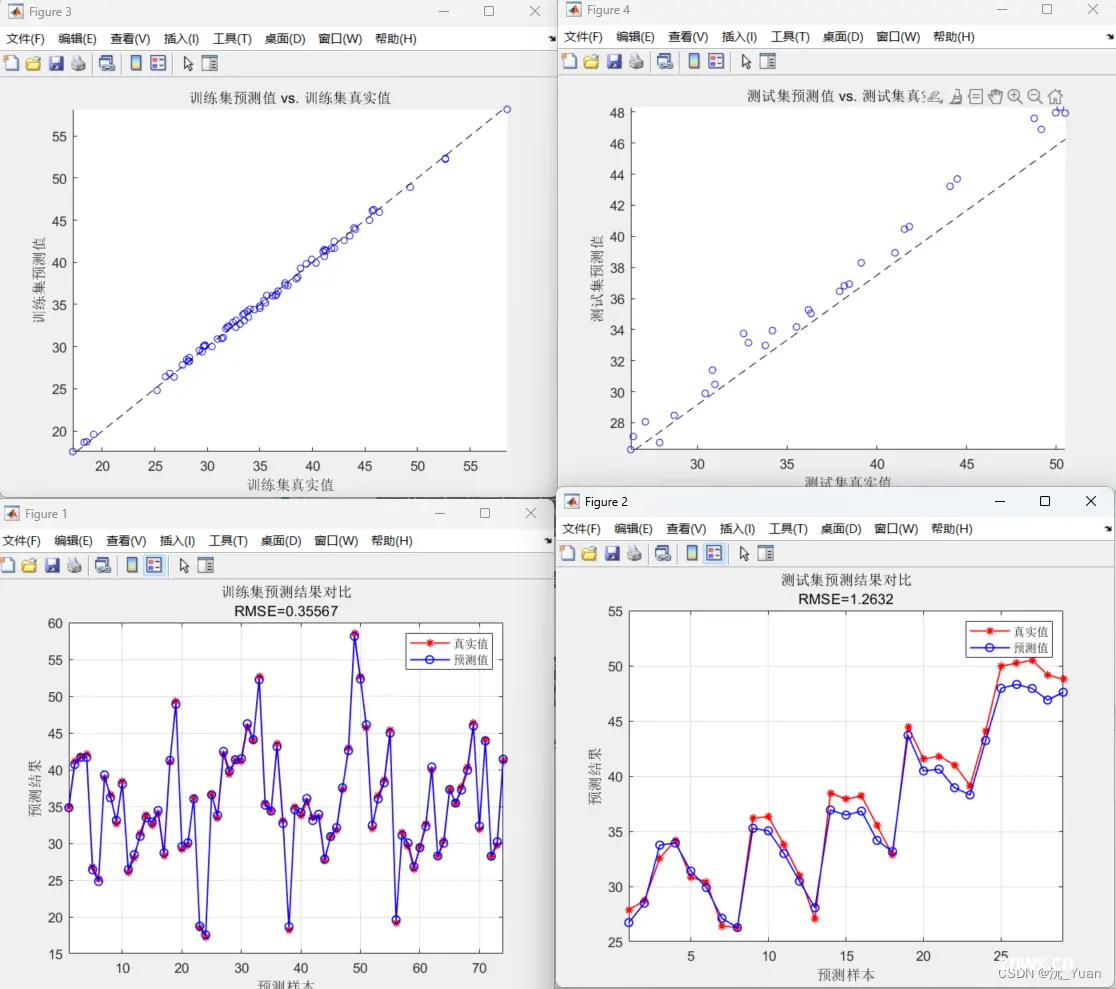
评价指标

完整下载链接:https://mbd.pub/o/bread/ZpaVlJZy
免费下载喔,如果觉得可以的话,欢迎支持博主主页其它付费代码
😘😘😘😘😘💕💕💕💕💕
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。