【C++】AVL树(旋转、平衡因子)
秦jh_ 2024-07-14 14:05:02 阅读 65
🌈个人主页:秦jh_-CSDN博客
🔥 系列专栏:https://blog.csdn.net/qinjh_/category_12575764.html?spm=1001.2014.3001.5482

目录
前言
AVL树的概念
节点
插入
AVL树的旋转
新节点插入较高左子树的左侧---左左:右单旋
新节点插入较高右子树的右侧---右右:左单旋
新节点插入较高左子树的右侧---左右:先左单旋再右单旋
新节点插入较高右子树的左侧---右左:先右单旋再左单旋
AVL树的验证
AVL树的性能
完整代码
前言
💬 hello! 各位铁子们大家好哇。
今日更新了AVL树的相关内容
🎉 欢迎大家关注🔍点赞👍收藏⭐️留言📝
AVL树的概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查 找元素相当于在顺序表中搜索元素,效率低下。
解决方案:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
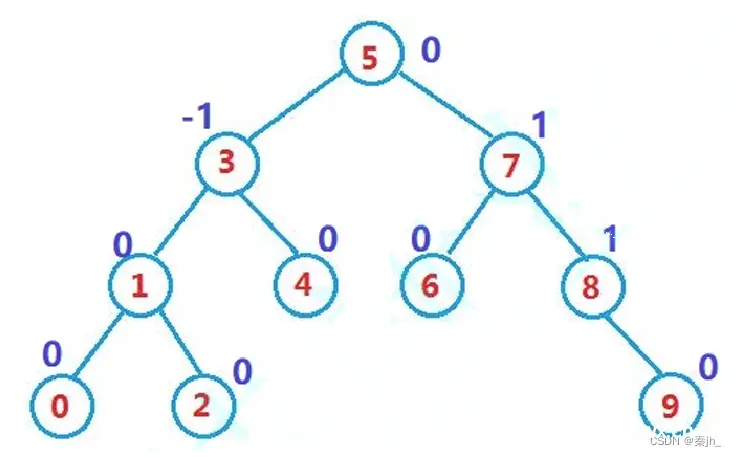
它的左右子树都是AVL树左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
如果一棵二叉搜索树是高度平衡的,它就是AVL树。
插入的总体原则:
按照搜索树规则插入更新插入节点的祖先节点的平衡因子。
如果插入在父亲左边,父亲的平衡因子--。如果插入在父亲右边,父亲的平衡因子++。父亲平衡因子==0,则父亲所在子树高度不变,不再继续往上更新,插入结束。父亲平衡因子==1or-1,父亲所在子树高度变了,继续往上更新。父亲平衡因子==2or-2,父亲所在子树已经不平衡了,需要旋转处理。
节点

插入
<code>bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first > kv.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
//更新平衡因子
while (parent)
{
if (cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
if (parent->_bf == 0)
{
//更新结束
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
//继续往上更新
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
//当前子树出问题了,需要旋转平衡一下
break;
}
else
{
//理论而言不可能出现该情况
assert(false);
}
}
return true;
}
上面是插入的大体流程,旋转操作还未给出。
AVL树的旋转
如果在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时必须调整树的结构, 使之平衡化。根据节点插入位置的不同,AVL树的旋转分为四种:
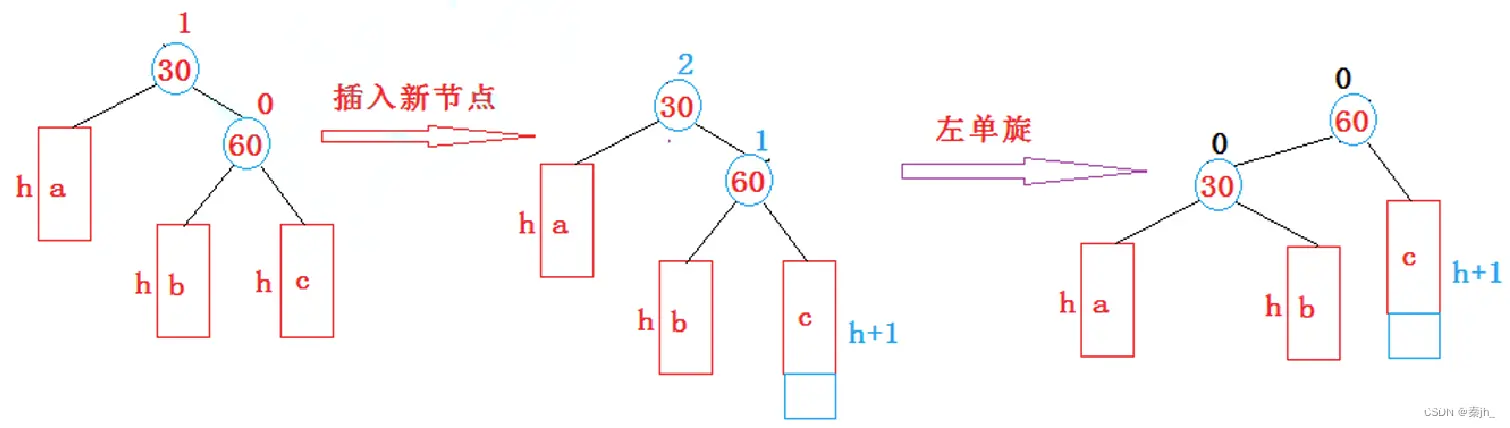
新节点插入较高左子树的左侧---左左:右单旋

这里以抽象图进行分析,因为具体的情况有很多种,无法画出。
注意:a子树的情况必须是插入后会引发祖先节点的更新,而不是只是内部变化。如下图情况就不符合要求。
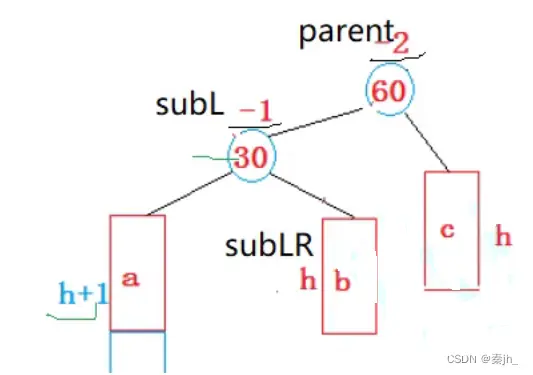
旋转流程:新节点插入在a树中,导致以60为根的二叉树不平衡。所以就要右单旋。
右单旋:把60的左子树高度减少,即把60取出来,让30的右子树变成60的左子树,再把以60为根的树变成30的右子树。30成为新的根。
<code>void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR) //节点可能为空
subLR->_parent = parent;
subL->_right = parent; //旧父节点变成subL的右节点
Node* ppNode = parent->_parent; //该不平衡节点可能不是根节点,所以要找到它的父节点
parent->_parent = subL;
if (parent == _root) //如果该节点是根节点
{
_root = subL;
_root->_parent = nullptr;
}
else //不平衡节点只是一棵子树
{
if (ppNode->_left == parent) //如果旧父节点等于爷爷节点的左节点,新父节点为爷爷节点的左节点
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode;//新父节点指向爷爷节点。
}
parent->_bf = subL->_bf = 0; //只需要修改这两个的平衡因子
}
新节点插入较高右子树的右侧---右右:左单旋
参考右单旋。
左单旋和右单旋的调用如下图:
新节点插入较高左子树的右侧---左右:先左单旋再右单旋

单旋用在一边一直高的情况。双旋是先一边高再另一边高的情况。
双旋的的原理就是把折线变成直线,再像处理直线一样旋转。
双旋可以复用单旋,但双旋主要要搞清平衡因子的变化。
第一种情况:
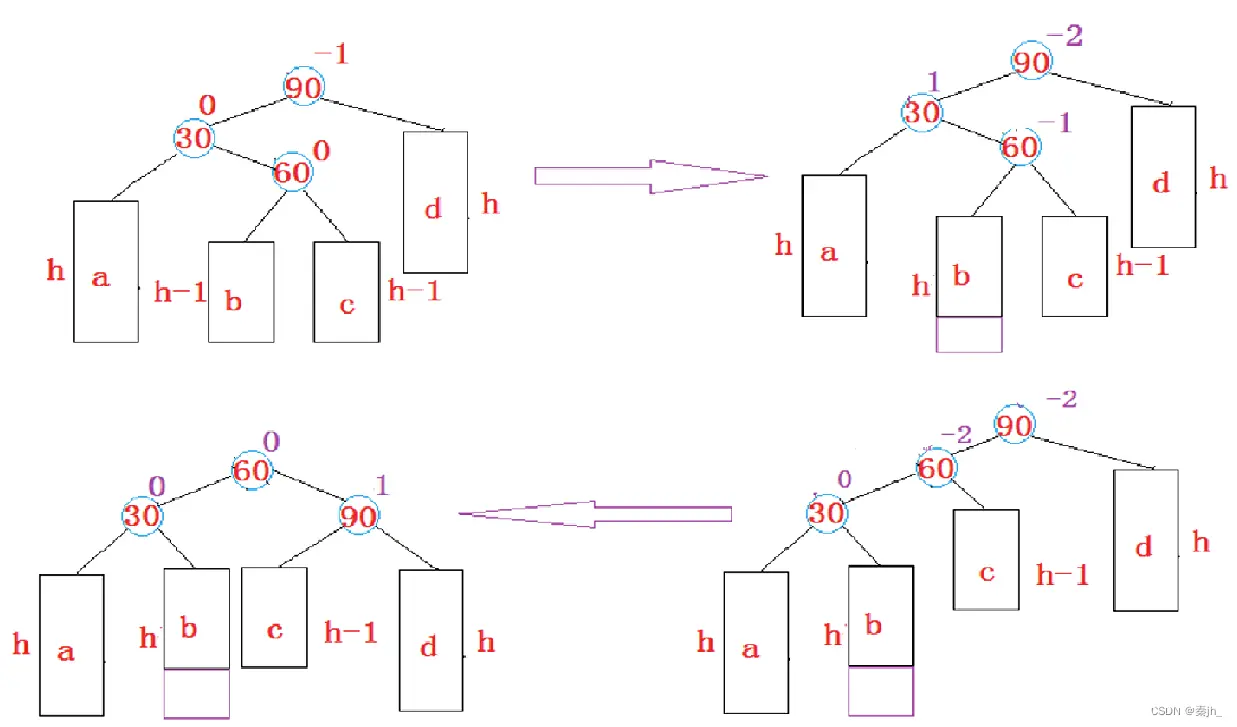
双旋的结果:60的左边给了30的右边,60的右边给了90的左边,30和90分别成为60的左右,60成为根。
上图是插入b引起的旋转,当插入c时是第二种情况,如下图:
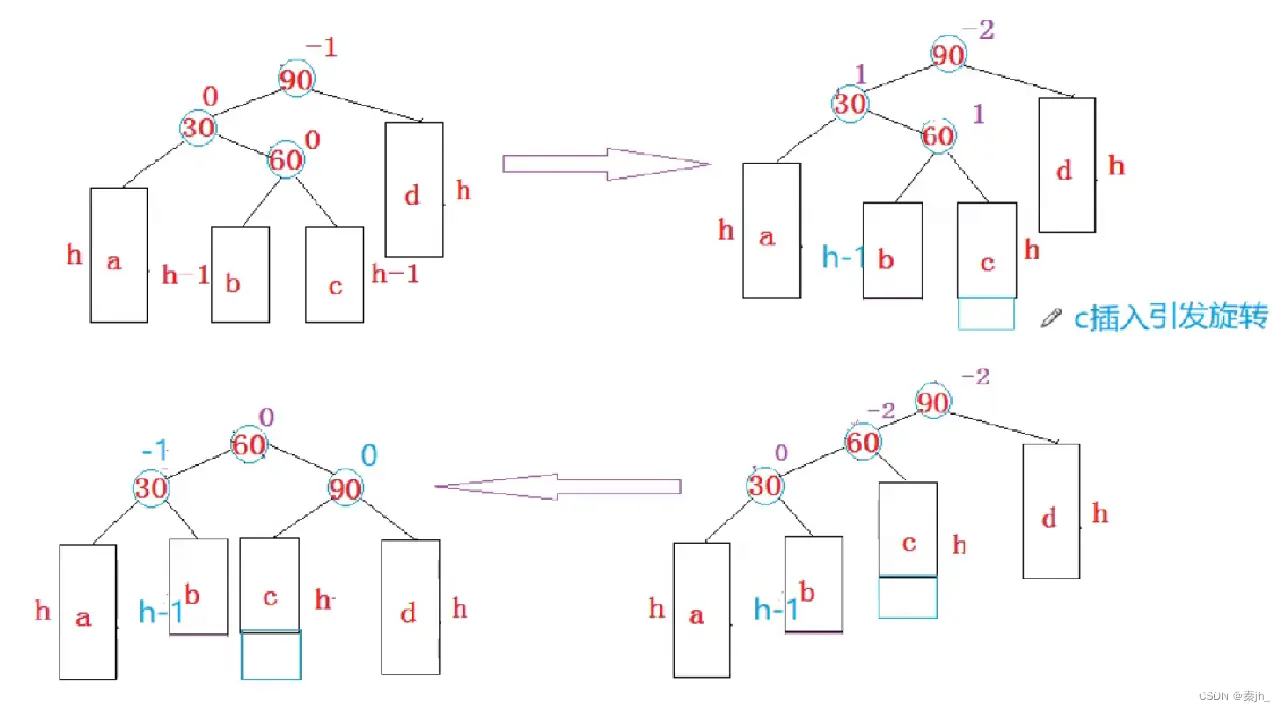
上面两种插入位置的不同,导致最终的平衡因子不同。
第三种情况:

h==0时,60就是新增节点,最终的平衡因子也不同。
<code>void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf; //记录未旋转前subLR的平衡因子
RotateL(parent->_left);
RotateR(parent);
if (bf == -1) //如果bf为-1,即插入在subLR的左边
{
subLR->_bf = 0;
subL->_bf = 0;
parent->_bf = 1;
}
else if (bf == 1) //插入在subLR的右边
{
subLR->_bf = 0;
subL->_bf = -1;
parent->_bf = 0;
}
else if (bf == 0)
{
subLR->_bf = 0;
subL->_bf = 0;
parent->_bf = 0;
}
else
{
assert(false);
}
}
新节点插入较高右子树的左侧---右左:先右单旋再左单旋

参考左右双旋,注意,这里也要讨论那三种情况。
<code>void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
subRL->_bf = 0;
if (bf == 1)
{
subR->_bf = 0;
parent->_bf = -1;
}
else if (bf == -1)
{
parent->_bf = 0;
subR->_bf = 1;
}
else
{
parent->_bf = 0;
subR->_bf = 0;
}
}
AVL树的验证
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
验证其为二叉搜索树。如果中序遍历可得到一个有序的序列,就说明为二叉搜索树验证其为平衡树。每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子) 节点的平衡因子是否计算正确

因为root是私有的,又因为需要递归检查每棵子树是否平衡,所以可以写一个私有的_IsBalance方法,通过公有的IsBalance方法来调用。
AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这 样可以保证查询时高效的时间复杂度,即O(logN)。 但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时, 有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。红黑树在经常进行增删的结构中性能比AVL树更优。
完整代码
<code>template<class K, class V>
struct AVLTreeNode
{
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
pair<K, V> _kv;
int _bf;
AVLTreeNode(const pair<K, V>& kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(kv)
,_bf(0)
{}
};
template<class K, class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first > kv.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
//更新平衡因子
while (parent)
{
if (cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
if (parent->_bf == 0)
{
//更新结束
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
//继续往上更新
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
//当前子树出问题了,需要旋转平衡一下
if (parent->_bf == -2 && cur->_bf == -1) //左边高,右单旋
{
RotateR(parent);
}
else if (parent->_bf == 2 && cur->_bf == 1)//右边高,左单旋
{
RotateL(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
break;
}
else
{
//理论而言不可能出现该情况
assert(false);
}
}
return true;
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < key)
{
cur = cur->_right;
}
else if (cur->_kv.first > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR) //节点可能为空
subLR->_parent = parent;
subL->_right = parent; //旧父节点变成subL的右节点
Node* ppNode = parent->_parent; //该不平衡节点可能不是根节点,所以要找到它的父节点
parent->_parent = subL;
if (parent == _root) //如果该节点是根节点
{
_root = subL;
_root->_parent = nullptr;
}
else //不平衡节点只是一棵子树
{
if (ppNode->_left == parent) //如果旧父节点等于爷爷节点的左节点,新父节点为爷爷节点的左节点
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode;//新父节点指向爷爷节点。
}
parent->_bf = subL->_bf = 0; //只需要修改这两个的平衡因子
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
subR->_left = parent;
Node* ppNode = parent->_parent;
parent->_parent = subR;
if (parent == _root)
{
_root = subR;
_root->_parent = nullptr;
}
else
{
if (ppNode->_right == parent)
{
ppNode->_right = subR;
}
else
{
ppNode->_left = subR;
}
subR->_parent = ppNode;
}
parent->_bf = subR->_bf = 0;
}
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
subRL->_bf = 0;
if (bf == 1)
{
subR->_bf = 0;
parent->_bf = -1;
}
else if (bf == -1)
{
parent->_bf = 0;
subR->_bf = 1;
}
else
{
parent->_bf = 0;
subR->_bf = 0;
}
}
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf; //记录未旋转前subLR的平衡因子
RotateL(parent->_left);
RotateR(parent);
if (bf == -1) //如果bf为-1,即插入在subLR的左边
{
subLR->_bf = 0;
subL->_bf = 0;
parent->_bf = 1;
}
else if (bf == 1) //插入在subLR的右边
{
subLR->_bf = 0;
subL->_bf = -1;
parent->_bf = 0;
}
else if (bf == 0)
{
subLR->_bf = 0;
subL->_bf = 0;
parent->_bf = 0;
}
else
{
assert(false);
}
}
bool IsBalance()
{
return _IsBalance(_root);
}
int Height() //树的高度
{
return _Height(_root);
}
int Size() //插入的节点个数
{
return _Size(_root);
}
private:
int _Size(Node* root)
{
return root == nullptr ? 0 : _Size(root->_left) + _Size(root->_right) + 1;
}
int _Height(Node* root)
{
if (root == nullptr)
return 0;
return max(_Height(root->_left), _Height(root->_right)) + 1;
}
bool _IsBalance(Node* root)
{
if (root == nullptr)
return true;
intleftHeight = _Height(root->_left);
intrightHeight = _Height(root->_right);
//如果不平衡
if (abs(leftHeight - rightHeight) >= 2)
{
cout << root->_kv.first << endl;
return false;
}
//检查平衡因子是否正确
if (rightHeight - leftHeight != root->_bf)
{
cout << root->_kv.first << endl;
return false;
}
return _IsBalance(root->_left)
&& _IsBalance(root->_right);
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_InOrder(root->_right);
}
private:
Node* _root=nullptr;
};
void AVLTreeTest1()
{
//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
AVLTree<int,int> t1;
for (auto e : a)
{
t1.Insert({e,e});
cout <<"Insert:"<<e<<"->"<< t1.IsBalance() << endl;
}
t1.InOrder();
cout << t1.IsBalance() << endl;
}
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。
