A题 Legs

题目：

农夫约翰的农场又迎来了美好的一天。

农夫约翰到达他的农场后，他数了数 n条 腿。众所周知，只有鸡和牛生活在农场，鸡有 2 条腿，而牛有 4 条腿 。

假设农场主约翰计算了所有动物的腿，他的农场上能有的最小动物数量是多少？

输入

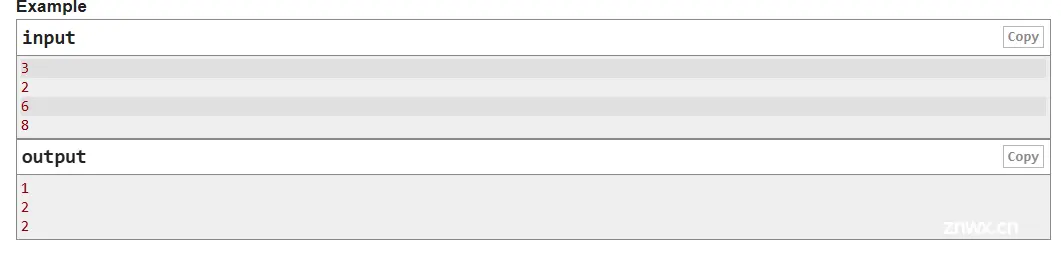
第一行包含单个整数 t ( 1 <= t <= 10^3 )ー测试用例的数量。

每个测试用例包含一个整数 n ( 2 <= n <= 2 * 10^3 ，n  是偶数 )。

输出

对于每个测试用例，输出一个整数，即农场主约翰可以在他的农场上养的动物的最小数量。

解题思路：

很简单的问题，类似于小学的鸡兔同笼问题，主要是贪心的思想，数量优先给牛，剩下的给鸡。

AC代码：

<code>#include<iostream>

using namespace std;

int n,t,sum;

int main(){

cin>>t;

while(t--){

sum=0;

cin>>n;

sum+=n/4;

sum+=n%4/2;

cout<<sum<<endl;

}

return 0;

}

B题 Scale

题目：

Tina有一个包含 n 行和 n 列的正方形网格。网格中的每个单元格都是 0 或 1 。Tina希望将网格减少因子 k （k 是 n 的除数）。

为此，Tina将网格拆分为 k * k 个不重叠的单元块，以便每个单元恰好属于一个块。然后，Tina用与块中的单元的值相等的单个单元来替换每个单元块。

保证同一块中的每个单元都具有相同的值。例如，以下演示显示了以因子 3 减少的网格。

输入

第一行包含 t（ 1 <= t <= 100 ）–测试用例的数量。

每个测试用例的第一行包含两个整数 n 和 k （ 1 <= n <= 1000 ， 1 <= k <= n ，

k 是 n的除数）—网格的行数和列数，以及Tina想要减少网格的因子。以下 n 行中的每一行都包含描述网格单元格的 n 字符。

每个字符为 0 或 1 。 k 块保证每个 k 具有相同的值。保证所有测试用例的 n 之和不超过 1000 。

输出

对于每个测试用例，在新行上输出减少因子 k 的网格。

解题思路：

emmm，好像没看懂

看了样例，理解了一会，才知道所缩小的因子就是行和列每隔k就输出一次即可。

AC代码：

<code>#include<iostream>

#include<cstring>

#include<vector>

using namespace std;

int t,n,k;

int main(){

cin>>t;

while(t--){

string s;

vector<string>v;

cin>>n>>k;

for(int i=0;i<n;i++){

cin>>s;

v.push_back(s);

}

for(int i=0;i<n;i+=k){

for(int j=0;j<n;j+=k){

cout<<v[i][j];

}

cout<<endl;

}

}

return 0;

}

C题 Sort

题目：

给出两个字符串 a 和 b ，长度为 n 。然后，您(被迫)回答q 个问题。对于每个查询，您都会得到一个由 l 和 r 限定的范围。在一个操作中，您可以选择整数 i ( l <= i <= r )

并设置 ai = x ，其中 x 是所需的任何字符。输出必须执行的最小操作数，以便 sorted(a[l..r]) = sorted(b[l..r]) 。您对一个查询执行的操作不会影响其他查询。

对于任意字符串 c ，sorted(c[l..r]) 表示由按字典顺序排序的字符 cl+1, ... , cr 组成的子字符串。

输入

第一行包含 t ( 1 <= t <= 1000 )–测试用例的数量。

每个测试用例的第一行包含两个整数 n 和 q ( 1 <= n, q <= 2 * 10^5 )

–两个字符串的长度和查询次数。

下一行包含长度为 n 的 a 。

保证 a 只包含小写拉丁字母。

下一行包含长度为 n 的 b 。

它保证 b 只包含小写拉丁字母。以下 q 行包含两个整数 l 和 r ( 1 <= l <= r <= n )–查询的范围。

保证所有测试用例的 n 和 q 之和不超过 2 * 10^5 。

输出

对于每个查询，输出一个整数，即需要在新行中执行的最小操作数。

注意

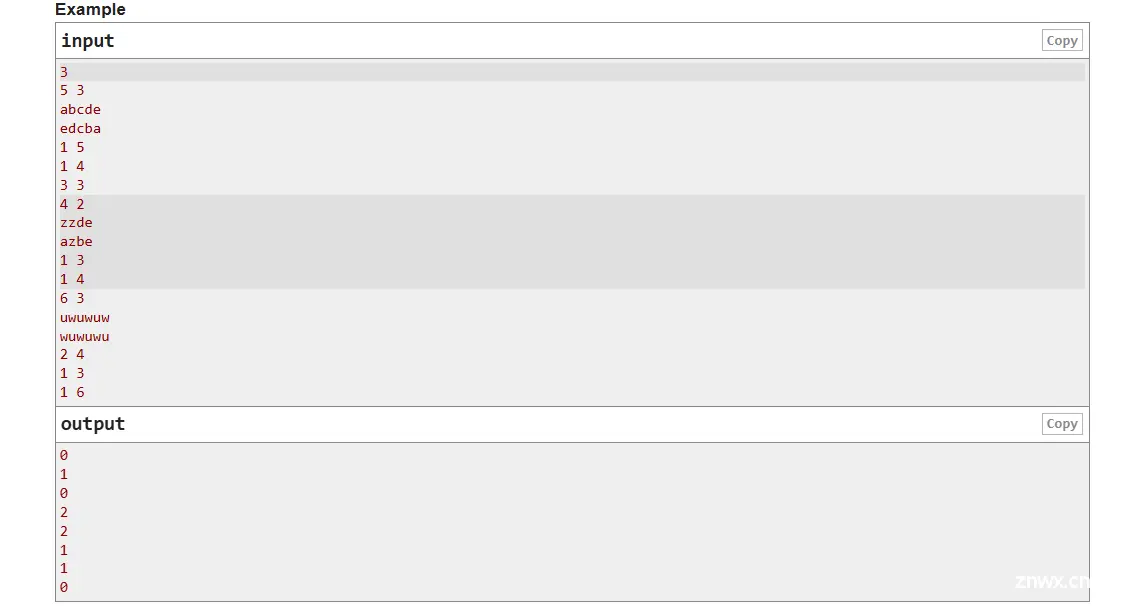
对于第一个查询， sorted(a[1..5]) =ABCDE和 sorted(b[1..5]) = ABCDE，因此不需要任何操作。

对于第二个查询，您需要设置 a1 = E。然后，sorted(a[1..4]) = sorted(b[1..4]) = BCDE。

解题思路：

题目看上去很简单，C++给了5s,题意主要就是给两个字符串，每次给一个左右区间，分别在这两个字符串上截取出来，按照sort排序规则，看两个字符串相差哪几个，可以进行操作修改其值，最终达到sort相同的目的。刚开始的思路是模拟，按照题目给的l,r截取出来，sort一下看看是不是相同，不一样的就进行一次操作。但是忘记了重复这一个问题，所以就要考虑另一种做法，看了大佬的题解，思路是开26个桶，就是26个字母的出现次数，再加上一个维度表示在下标为i之前的出现次数，当要查询区间为l、r时,直接在遍历这26个桶，看一下每个字母在字符串a跟字符串b的出现次数，做一下差值，就是它们不相同的个数，由于只需要改一个字符串即可，最后答案/2，主要的思想跟前缀和差不多。

AC代码：

<code>#include <bits/stdc++.h>

using namespace std;

using ll = long long;

const int N = 200005;

void solve(){

int n, q;

cin >> n >> q;

string s1, s2;

cin >> s1 >> s2;

s1 = " " + s1;

s2 = " " + s2;

vector<vector<int>> a(n+1, vector<int>(100));//字符串a前i个字符，字母j出现的次数

vector<vector<int>> b(n+1, vector<int>(100));//字符串b前i个字符，字母j出现的次数

for(int i = 1; i <= n; i++){

a[i] = a[i-1];//加上前面统计的次数

b[i] = b[i-1];

a[i][s1[i]-'a']++;//更新当前字符的个数

b[i][s2[i]-'a']++;

}

while(q--){

int l,r;

cin >> l >> r;

int ans = 0;

for(int i = 0; i < 26; i++){

ans+=abs(a[r][i] - a[l-1][i] - (b[r][i] - b[l-1][i]));//两个字符串的字符差值

}

cout << ans / 2 << '\n';

}

}

int main(){

int T = 1; cin >> T;

while(T--)

{

solve();

}

return 0;

}

D题 Fun

题目：

数数很有趣！                                                                                                             —SATYAM343

给定两个整数 n 和 x ，求正整数的三元组（ a,b,c ）的个数，使得 ab + ac + bc <= n 和 a + b + c <= x 。

请注意，（例如（ 1, 1, 2 ）和（ 1, 2, 1 ）被视为不同）和 a 、 b 、 c 必须严格大于 0 。

输入

第一行包含单个整数 t （ 1 <= t <= 10^4 ）—测试用例的数量。

每个测试用例包含两个整数 n 和 x （ 1 <= n,x <= 10^6 ）。

保证所有测试用例的 n 之和不超过 10^6 ，并且所有测试用例的 x 之和不超过 10^6 。

输出

输出单个整数-满足 ab + ac + bc <= n 和 a + b + c <= x 的正整数的三元组（ a,b,c ）的数目。

注意

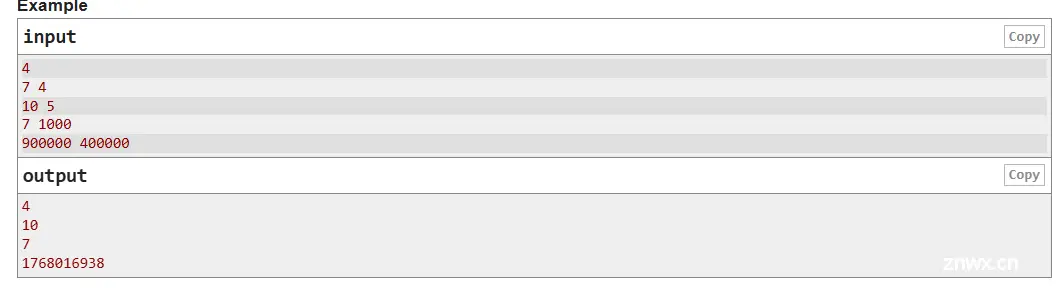
在第一个测试用例中，三元组是（ 1, 1, 1 ）、（ 1, 1, 2 ）、（ 1, 2, 1 ）和（ 2, 1, 1 ）。

在第二个测试用例中，三元组是（ 1, 1, 1 ）、（ 1, 1, 2 ）、（ 1, 1, 3 ），（ 1, 2, 1) ，（ 1, 2, 2 ），（ 1, 3, 1 ）和（ 2, 1, 1 ）以及（ 2, 1, 2 ）和（ 3, 1, 1 ）。

解题思路：

题目说的很简单，主要就是两个式子，分别是ab + ac + bc <= n 和 a + b + c <= x，如果直接求，肯定会超时，有式子肯定就是数学问题了，考虑化简，ab+ac+bc<=n  ab+(a+b)c<=n   c<=(n-ab)/(a+b)  第二个式子a+b+c<=x  c<=x-(a+b) 第一个式子我们将（a+b)与ab看成一个整体，如果a跟b知道了，那么（a+b)跟 ab就知道了，那么c也就知道了，第一个式子在最坏的情况下a*b=1，a+b=2,那么c<=（n-1）/2，c就有(n-1)/2种情况，再不寄一点a=2,b=1,则c<=(n-2)/3，也可以a=1,b=2因为（2，1，c)跟（1，2，c）是不一样的，我们这样可以去枚举a跟b，类似第二个式子最坏的情况下a=1,b=1,c<=x-2,c就有x-2种情况满足条件。再不寄的情况下a=2,b=1，c<=x-3。综上a,b,c要同时满足这两个式子，那么哪一个式子的限制条件大，我们就取谁。

AC代码：

<code>#include<bits/stdc++.h>

using namespace std;

int main(){

int t;

cin >> t;

while(t--){

int n, x;

cin >> n >> x;

long long ans = 0;

for(long long a = 1; a <= n && a <= x; a++){

for(long long b = 1; a*b <= n && a+b <= x; b++){

ans += min(max(x-a-b,0LL),max(n-a*b,0LL)/(a+b));//涉及到减法，要与零取最大值，防止为负数

}

}

cout << ans << "\n";

}

return 0;

}