CORDIC算法解释及verilog HDL实现(圆坐标系)
cnblogs 2024-08-18 17:39:00 阅读 94
CORDIC算法原理阐述
CORDIC(Coordinate Rotation Digital Computer)算法,即坐标旋转数字计算方法,是J.D.Volder1于1959年首次提出,主要用于三角函数、双曲线、指数、对数的计算。
伪旋转
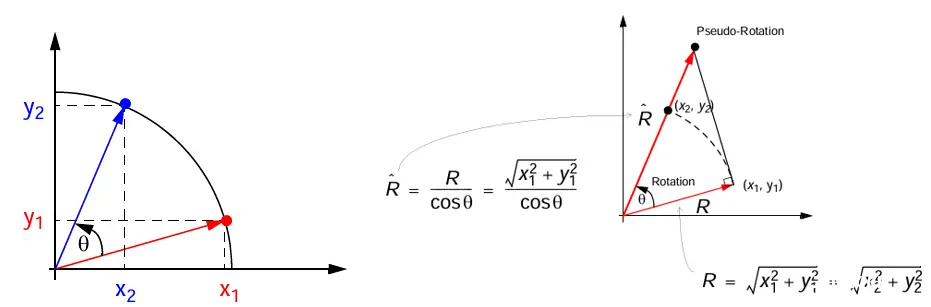
在笛卡尔坐标平面(下方左图)由 \(({x_1},{y_1})\) 旋转 θ 角度至 \(({x_2},{y_2})\) 得到:\(({\hat x_2},{\hat y_2})\) ;
提出因数 \(\cos \theta\) ,方程转化为:\(\left\{ {\matrix{
{{x_2} = \cos \theta ({x_1} - {y_1}\tan \theta )} \cr
{{y_2} = \cos \theta ({y_1} + {x_1}\tan \theta )} \cr
} } \right.\);
待去除 \(\cos \theta\) 项,得到“伪旋转”公式\(\left\{ {\matrix{
{{{\hat x}_2} = {x_1} - {y_1}\tan \theta } \cr
{{{\hat y}_2} = {y_1} + {x_1}\tan \theta } \cr
} } \right.\)。
经“伪旋转”后,向量 R 模值将增加 $1/\cos \theta $ 倍(角度保持一致)。
角度累加器
为便于FPGA硬件实现(正切项需改为移位操作):以 $ \tan {\theta ^i} = {2^{ - i}}$ 设定旋转角度 θ ;
故方程可转换为\(\left\{ {\matrix{
{{{\hat x}_{_2}} = {x_1} - {y_1}{2^{ - i}}} \cr
{{{\hat y}_{_2}} = {y_1} + {x_1}{2^{ - i}}} \cr
} } \right.\) 或 \(\left[ {\matrix{
{{{\hat x}_{_2}}} \cr
{{{\hat y}_{_2}}} \cr
} } \right] = \left[ {\matrix{
1 & { - {2^{ - i}}} \cr
{{2^{ - i}}} & 1 \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{y_1}} \cr
} } \right]\)。
其中矩阵 \(\left[ {\matrix{
1 & { - {2^{ - i}}} \cr
{{2^{ - i}}} & 1 \cr
} } \right]\) 可进行拆分为多个类似矩阵乘积,即旋转角度 θ ,可拆分为多次小的旋转(下图为对应的反正切角度表)。
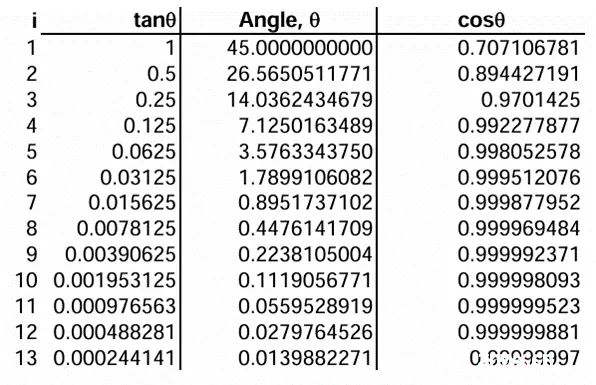
由于旋转角度 θ 可为任意值,故将旋转变换采用迭代算法实现,即多次角度迭代关系无限趋近于目标θ角度(以 θ 旋转角度限制)。以55°度旋转角为例逼近55° = 45.0° + 26.6° -14.0°- 7.1° + 3.6° + 1.8° - 0.9°。
旋转过程需引入一个判决因子 \({d_i}\) ,用于确定角度旋转的方向。
根据判决因子 \({d_i}\) 来设定一个角度累加器:$\eqalign{
& {z^{(i + 1)}} = {z^{(i)}} - {d_i}{\theta ^{(i)}} \cr
& where:{d_i} = \pm 1 \cr} $,其中z(旋转角度差)无限趋近于0。
并且伪旋转可表示为\(\left\{ {\matrix{
{{x^{(i + 1)}} = {x^{(i)}} - {d_i}({2^{ - i}}{y^{(i)}})} \cr
{{y^{(i + 1)}} = {y^{(i)}} + {d_i}({2^{ - i}}{x^{(i)}})} \cr
} } \right.\)。
象限预处理
当然,每次旋转的方向都影响到最终要旋转的累积角度,角度范围大致为: $ - 99.7 \le \theta \le 99.7$。对于范围外的角度,需要使用三角恒等式转化进行“预处理”,即象限判断。

因此,原始算法规整为使用向量的伪旋转来表示迭代移位-相加算法,即:\(\left\{ {\matrix{
{{x^{(i + 1)}} = {x^{(i)}} - {d_i}({2^{ - i}}{y^{(i)}})} \cr
{{y^{(i + 1)}} = {y^{(i)}} + {d_i}({2^{ - i}}{x^{(i)}})} \cr
{{z^{(i + 1)}} = {z^{(i)}} - {d_i}{\theta ^{(i)}}} \cr
} } \right.\),
前面提到了,在进行“伪旋转”操作时,每次迭代运算都忽略了\(\cos \theta\)项,最终得到的 \({x^{(n)}},{y^{(n)}}\) 被伸缩了 \({k_n}\)倍
${k_n} = \prod\limits_n {({1 \over {\cos {\theta ^{(i)}}}})} = \prod\limits_n {(\sqrt {1 + {2^{( - 2i)}}} )} $ (伸缩因子)。
对 \({k_n}\) 求无限积,${k_n} = \prod\limits_n {(\sqrt {1 + {2^{( - 2i)}}} )} \to 1.6476,as:n \to \infty $( \(1/{k_n} = 0.6073\) )
若已知执行的迭代次数,便可直接求得 \({k_n}\) 最终值。
关于圆坐标系下,CORDIC算法应用包括旋转模式和向量模式两种:
旋转模式
应用场景:已知相角angle,用Cordic算法计算其正弦和余弦值。
具体过程:判决因子\({d_i}{\rm{ = sign}}({z^{(i)}}) \Rightarrow {z^{(i)}} \to 0\),N次迭代后得到\(\left\{ {\matrix{
{{x^{(n)}} = {k_n}({x^{(0)}}\cos {z^{(0)}} - {y^{(0)}}\sin {z^{(0)}})} \cr
{{y^{(n)}} = {k_n}({y^{(0)}}\cos {z^{(0)}} + {x^{(0)}}\sin {z^{(0)}})} \cr
{{z^{(n)}} = 0} \cr
} } \right.\)( \({z^{(0)}}\) = θ)通过设置 \({x^{(0)}} = {1 \over {{k_n}}}{{\rm{y}}^{(0)}} = 0\),可最终求到 $\cos \theta、 \sin \theta $ 。
向量模式
应用场景:已知坐标,用cordic算法计算相角和幅值。
具体过程:直角坐标系转换的极坐标系,迭代过程变化为\(\left\{ {\matrix{
{{x^{(i + 1)}} = {x^{(i)}} - {d_i}({2^{ - i}}{y^{(i)}})} \cr
{{y^{(i + 1)}} = {y^{(i)}} + {d_i}({2^{ - i}}{x^{(i)}})} \cr
{{z^{(i + 1)}} = {z^{(i)}} - {d_i}{\theta ^{(i)}}} \cr
} } \right.\),
其中判决因子 \({d_i}{\rm{ = - sign}}({x^{(i)}}{y^{(i)}}) \Rightarrow {y^{(i)}} \to 0\),N次迭代得到:\(\left\{ {\matrix{
{{x^{(n)}} = {k^{(n)}}\sqrt {x_0^2 + y_0^2} } \cr
{{y^{(n)}} = 0} \cr
{{z^{(n)}} = {z^{(0)}} + {{\tan }^{ - 1}}({y_0}/{x_0})} \cr
{{k^{(n)}} = \prod\limits_n {\sqrt {1 + {2^{ - 2i}}} } } \cr
} } \right.\),
通过设定\({x^{(0)}} = 1,{z^{(0)}} = 0\),可最终求得 \({\tan ^{ - 1}}{y^{(0)}}\)。
Verilog HDL实现CORDIC
针对\(\left\{ {\matrix{
{{x^{(i + 1)}} = {x^{(i)}} - {d_i}({2^{ - i}}{y^{(i)}})} \cr
{{y^{(i + 1)}} = {y^{(i)}} + {d_i}({2^{ - i}}{x^{(i)}})} \cr
{{z^{(i + 1)}} = {z^{(i)}} - {d_i}{\theta ^{(i)}}} \cr
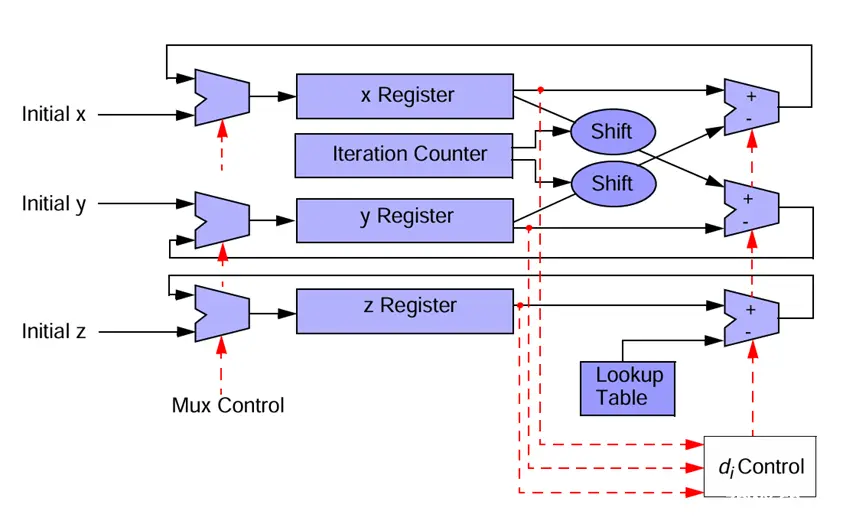
} } \right.\) ,每次迭代计算需要2次移位 \(({x^{(i)}{,y^{(i)}}})\) 、1次查找表\({\theta ^{(i)}}\)、3次加法(x、y、z累加)。
对应的CORDIC硬件结构如下:
在Cordic—旋转模式下,Matlab代码实现:
点击查看代码
<code>%% ***********************************************************************************
% 圆坐标系下:Cordic—旋转模式
% 已知相角angle,计算其正弦和余弦值。基本公式如下:
% x(k+1) = x(k) - d(k)*y(k)*2^(-k)
% y(k+1) = y(k) + d(k)*x(k)*2^(-k)
% z(k) = z(k) - d(k)*actan(2^(-k))
%% ***********************************************************************************
clear;close all;clc;
angle = 30; %设定旋转角度
% 初始化-------------------------------
N = 16; %迭代次数
tan_table = 2.^-(0 : N-1);
angle_LUT = atan(tan_table); %建立arctan&angle查找表
An = 1;
for k = 0 : N-1
An = An*(1/sqrt(1 + 2^(-2*k)));
end
Kn = 1/An;%计算归一化伸缩因子参数:Kn = 1.6476,1/Kn = 0.6073
Xn = 1/Kn; %相对于X轴上开始旋转
Yn = 0;
Zi = angle/180*pi; %角度转化为弧度
% cordic算法计算-------------------------------
if (Zi > pi/2) % 先做象限判断,得到相位补偿值
Zi = Zi - pi;
sign_x = -1;
sign_y = -1;
elseif (Zi < -pi/2)
Zi = Zi + pi;
sign_x = -1;
sign_y = -1;
else
sign_x = 1;
sign_y = 1;
end
for k = 0 : N-1 % 迭代开始
Di = sign(Zi);
x_temp = Xn;
Xn = x_temp - Di*Yn*2^(-k);
Yn = Yn + Di*x_temp*2^(-k);
Zi = Zi - Di*angle_LUT(k+1);
end
cos_out = sign_x*Xn; %余弦输出
sin_out = sign_y*Yn; %正弦输出
Verilog HDL在旋转模式下,程序:
点击查看代码
module Cordic_rotate_mode(
input sys_clk ,
input sys_rst ,
input signed [31:0] angle ,
output reg [31:0] cosout ,
output reg [31:0] sinout
);
//旋转角度查找表
wire [31:0]rot[15:0];
assign rot[0] = 32'd2949120 ; //45.0000度*2^16
assign rot[1] = 32'd1740992 ; //26.5651度*2^16
assign rot[2] = 32'd919872 ; //14.0362度*2^16
assign rot[3] = 32'd466944 ; //7.1250度*2^16
assign rot[4] = 32'd234368 ; //3.5763度*2^16
assign rot[5] = 32'd117312 ; //1.7899度*2^16
assign rot[6] = 32'd58688 ; //0.8952度*2^16
assign rot[7] = 32'd29312 ; //0.4476度*2^16
assign rot[8] = 32'd14656 ; //0.2238度*2^16
assign rot[9] = 32'd7360 ; //0.1119度*2^16
assign rot[10] = 32'd3648 ; //0.0560度*2^16
assign rot[11] = 32'd1856 ; //0.0280度*2^16
assign rot[12] = 32'd896 ; //0.0140度*2^16
assign rot[13] = 32'd448 ; //0.0070度*2^16
assign rot[14] = 32'd256 ; //0.0035度*2^16
assign rot[15] = 32'd128 ; //0.0018度*2^16
//FSM_parameter
localparam IDLE = 2'd0;
localparam WORK = 2'd1;
localparam ENDO = 2'd2;
reg [1:0] state ;
reg [1:0] next_state ;
reg [3:0] cnt;
always @(posedge sys_clk or negedge sys_rst)begin
if(!sys_rst)
next_state <= IDLE;
else begin
state <= next_state;
case(state)
IDLE:next_state <= WORK;
WORK:next_state <= cnt == 15 ? ENDO:WORK;
ENDO:next_state <= IDLE;
default:next_state <= IDLE;
endcase
end
end
reg signed [31:0] x_shift;
reg signed [31:0] y_shift;
reg signed [31:0] z_rot;
wire D_sign;
assign D_sign= z_rot[31];
always @(posedge sys_clk) begin
case(state)
IDLE:
begin
x_shift <= 32'd39800;
y_shift <= 32'd0;
z_rot <= (angle<<16);
end
WORK:
if(D_sign)begin
x_shift <= x_shift + (y_shift>>>cnt);
y_shift <= y_shift - (x_shift>>>cnt);
z_rot <= z_rot + rot[cnt];
end
else begin
x_shift <= x_shift - (y_shift>>>cnt);
y_shift <= y_shift + (x_shift>>>cnt);
z_rot <= z_rot - rot[cnt];
end
ENDO:
begin
cosout <= x_shift;
sinout <= y_shift;
end
default :;
endcase
end
always @(posedge sys_clk or negedge sys_rst) begin
if(!sys_rst)
cnt <= 4'd0;
else if(state == IDLE && next_state == WORK)
cnt <= 4'd0;
else if(state==WORK)begin
if(cnt<4'd15)
cnt <= cnt + 1'b1;
else
cnt <= cnt;
end
else
cnt <= 4'd0;
end
endmodule
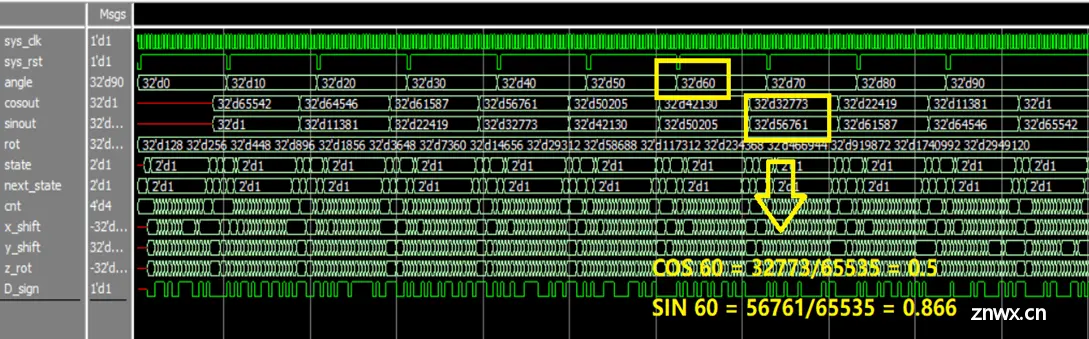
设定多种角度值,仿真如下图:
在Cordic—向量模式下,Matlab代码实现:
点击查看代码
<code>%% ***********************************************************************************
% 圆坐标系下:Cordic—向量模式
% 已知坐标,用cordic算法计算相角和幅值。基本公式如下:
% x(k+1) = x(k) - d(k)*y(k)*2^(-k)
% y(k+1) = y(k) + d(k)*x(k)*2^(-k)
% z(k) = z(k) - d(k)*actan(2^(-k))
%% ***********************************************************************************
clear;close all;clc;
% 初始化----------------------------------------
Xn = -1;
Yn = sqrt(3);
Zi = 0;
Di = 0;
N = 16; %迭代次数
tan_table = 2.^-(0 : N-1);
angle_LUT = atan(tan_table);
An = 1;
for k = 0 : N-1
An = An*(1/sqrt(1 + 2^(-2*k)));
end
Kn = 1/An;%计算归一化伸缩因子参数:Kn = 1.6476,1/Kn = 0.6073
% cordic算法计算-------------------------------
if (Xn==0 && Yn==0) %移至原点,未旋转角度
radian_out = 0;
amplitude_out = 0;
else % 先做象限判断,得到相位补偿值
if (Xn > 0) %第一、四象限:(-pi/2,0)/(0,pi/2)-->Zn
phase_shift = 0;
elseif (Yn < 0) %第三象限:(-pi,-pi/2)-->预旋转-pi,Zn+pi/2
phase_shift = -pi;
else %第二象限:(pi/2,pi)-->预旋转pi,Zn-pi/2
phase_shift = pi;
end
for k = 0 : N-1 % 迭代开始
Di = -sign(Xn*Yn);
x_temp = Xn;
Xn = x_temp - Di*Yn*2^(-k);
Yn = Yn + Di*x_temp*2^(-k);
Zi = Zi - Di*angle_LUT(k+1);
end
radian_out = Zi + phase_shift; %弧度输出
amplitude_out = abs(Xn)/Kn; %幅值输出
end
angle_out = radian_out*180/pi; %相角输出:角度(度)=角度(弧度)x pi/180
Verilog HDL在向量模式下,程序:
点击查看代码
module Cordic_vector_mode(
input sys_clk ,
input sys_rst ,
input signed [31:0] x ,
input signed [31:0] y ,
output reg [31:0] phase ,
output reg [31:0] mo_value
);
//旋转角度查找表
wire [31:0]rot[15:0];
assign rot[0] = 32'd2949120 ; //45.0000度*2^16
assign rot[1] = 32'd1740992 ; //26.5651度*2^16
assign rot[2] = 32'd919872 ; //14.0362度*2^16
assign rot[3] = 32'd466944 ; //7.1250度*2^16
assign rot[4] = 32'd234368 ; //3.5763度*2^16
assign rot[5] = 32'd117312 ; //1.7899度*2^16
assign rot[6] = 32'd58688 ; //0.8952度*2^16
assign rot[7] = 32'd29312 ; //0.4476度*2^16
assign rot[8] = 32'd14656 ; //0.2238度*2^16
assign rot[9] = 32'd7360 ; //0.1119度*2^16
assign rot[10] = 32'd3648 ; //0.0560度*2^16
assign rot[11] = 32'd1856 ; //0.0280度*2^16
assign rot[12] = 32'd896 ; //0.0140度*2^16
assign rot[13] = 32'd448 ; //0.0070度*2^16
assign rot[14] = 32'd256 ; //0.0035度*2^16
assign rot[15] = 32'd128 ; //0.0018度*2^16
//FSM_parameter
localparam IDLE = 2'd0;
localparam WORK = 2'd1;
localparam ENDO = 2'd2;
reg [1:0] state ;
reg [1:0] next_state ;
reg [3:0] cnt;
reg signed [31:0] x_shift;
reg signed [31:0] y_shift;
reg signed [31:0] z_rot;
always @(posedge sys_clk or negedge sys_rst)begin
if(!sys_rst)
next_state <= IDLE;
else begin
state <= next_state;
case(state)
IDLE:next_state <= WORK;
WORK:next_state <= cnt == 15 ? ENDO:WORK;
ENDO:next_state <= IDLE;
default:next_state <= IDLE;
endcase
end
end
wire D_sign;
assign D_sign=~y_shift[31];
always @(posedge sys_clk) begin
case(state)
IDLE:
begin
x_shift <= x;
y_shift <= y;
z_rot <= 0;
end
WORK:
if(D_sign)begin
x_shift <= x_shift + (y_shift>>>cnt);
y_shift <= y_shift - (x_shift>>>cnt);
z_rot <= z_rot + rot[cnt];
end
else begin
x_shift <= x_shift - (y_shift>>>cnt);
y_shift <= y_shift + (x_shift>>>cnt);
z_rot <= z_rot - rot[cnt];
end
ENDO:
begin
phase <= z_rot>>>16;
mo_value <= (x_shift>>>16)*0.6073;
end
default :;
endcase
en
always @(posedge sys_clk or negedge sys_rst) begin
if(!sys_rst)
cnt <= 4'd0;
else if(state == IDLE && next_state == WORK)
cnt <= 4'd0;
else if(state==WORK)begin
if(cnt<4'd15)
cnt <= cnt + 1'b1;
else
cnt <= cnt;
end
else
cnt <= 4'd0;
end
endmodule
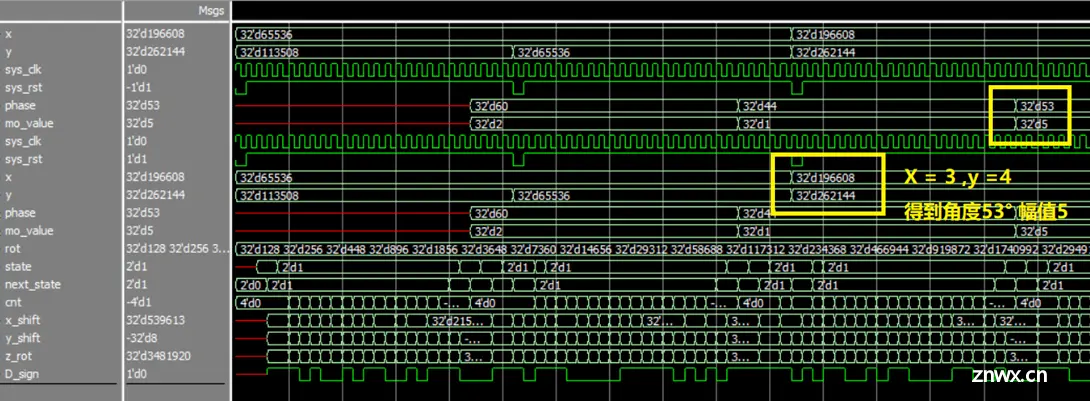
设定三种不同x,y值,仿真如下图:
本篇文章中使用的Verilog程序模块,若有需见网页左栏Gitee仓库链接:https://gitee.com/silly-big-head/little-mouse-funnyhouse/tree/FPGA-Verilog/
上一篇: SpringBoot文档之SpringApplication的阅读笔记
下一篇: 【Java】Windows系统中Java环境变量配置指南:详细配置JAVA_HOME和CLASSPATH(全网最详细的图文教程,建议收藏)
本文标签
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。