什么是算法复杂度？

        简单来说算法复杂度是用来衡量一个算法的优劣的，一个程序在运行时，对运行时间和运行空间有要求，即时间复杂度和空间复杂度。

目录

什么是算法复杂度？

大O的渐近表达式

时间复杂度示例

空间复杂度示例

 常见复杂度对比：

大O的渐近表达式

        时间复杂度，我们常常使用大O的渐近表示法

推导大O阶的规则：

●时间复杂度函数式T(N)中，只保留高阶项，去掉那些低阶项。

（因为当N不断变大时，低阶项对结果的影响越来越小，当N无穷大时，就可以忽略不计了）

●如果最高阶项存在且不是1，则去除这个项目的常数系数。

（因为当N不断变大，这个系数对结果的影响不断变小，当N无穷大时，其就可以忽略不计了）

●T(N)如果没有N相关的项目，只有常数项，那么就用常数1替代所有加法。

时间复杂度示例

1.

<code>// 计算Func2的时间复杂度？

void Func2(int N)

{

int count = 0; //1次

for (int k = 0; k < 2 * N ; ++ k)

{

++count; //2*N次

}

int M = 10;

while (M--)

{

++count; //10次

}

printf("%d\n", count);

}

 得：T(N)=1+2*N+10

由第一条和第二条规则得到时间复杂度O(N).

2.

// 计算Func3的时间复杂度？

void Func3(int N, int M)

{

int count = 0;

for (int k = 0; k < M; ++ k) //M次

{

++count;

}

for (int k = 0; k < N ; ++ k) //N次

{

++count;

}

printf("%d\n", count);

}

 得：T(N)=M+N

由第一条规则或第二条规则得到时间复杂度O(N).

 （因为使用N代表其中增长速度快的哪一项，则忽略掉增长速度慢的那一项，当M和N增长速度一样时为2N，则忽略系数）

3.

// 计算Func4的时间复杂度？

void Func4(int N)

{

int count = 0;

for (int k = 0; k < 100; ++ k) //100次

{

++count;

}

printf("%d\n", count);

}

 得：T(N)=100

由第三条规则得到时间复杂度O(1).

4.

// 计算strchr的时间复杂度？

const char * strchr ( const char * str, int character)

{

const char* p_begin = s;

while (*p_begin != character)

{

if (*p_begin == '\0')

return NULL;

p_begin++;

}

return p_begin;

}

①最好情况

        str的第一个字符就等于character，得：T(N)=1，则时间复杂度为O(1).

②平均情况

        要查找的字符在str的中间，得：T(N)=N/2，则时间复杂度为O(N).

③最差情况

        要查找字符在str的末尾，得：T(N)=N，则时间复杂度为O(N).

一般的我们取最差情况来表示算法的时间复杂度

★某些算法存在分情况的时间复杂度

        ●最坏情况：任意输入规模的最大运行次数（上界）.

        ●平均情况：任意输入规模的平均次数.

        ●最好情况：任意输入规模的最小次数（下界）.

 5.

// 计算BubbleSort的时间复杂度？

void BubbleSort(int* a, int n)

{

assert(a);

for (size_t end = n; end > 0; --end)

{

int exchange = 0;

for (size_t i = 1; i < end; ++i)

{

if (a[i-1] > a[i])

{

Swap(&a[i-1], &a[i]);

exchange = 1;

}

}

if (exchange == 0)

break;

}

}

通过上面的分析，我们可尝试求出三种情况：

最坏情况：倒序，O(N^2)

平均情况：平均情况，O(N^2）

最好情况：有序，O(N)

6.

void func5(int n)

{

int cnt = 1;

while (cnt < n)

{

cnt *= 2;

}

}

分析得T(N)=log2n,即O(logn).

7.

// 计算阶乘递归Fac的时间复杂度？

long long Fac(size_t N)

{

if(0 == N)

return 1;

return Fac(N-1)*N;

}

时间复杂度：O(N).

空间复杂度示例

        空间复杂度的表示也使用大O表达式。

1.

// 计算BubbleSort的时间复杂度？

void BubbleSort(int* a, int n)

{

assert(a); //1次

for (size_t end = n; end > 0; --end) //一次

{

int exchange = 0; //一次

for (size_t i = 1; i < end; ++i) //一次

{

if (a[i-1] > a[i])

{

Swap(&a[i-1], &a[i]);

exchange = 1;

}

}

if (exchange == 0)

break;

}

}

空间复杂度：O(1).

// 计算阶乘递归Fac的空间复杂度？

long long Fac(size_t N)

{

if(N == 0)

return 1;

return Fac(N-1)*N;

}

开辟了N个函数栈帧，空间复杂度为O(N)

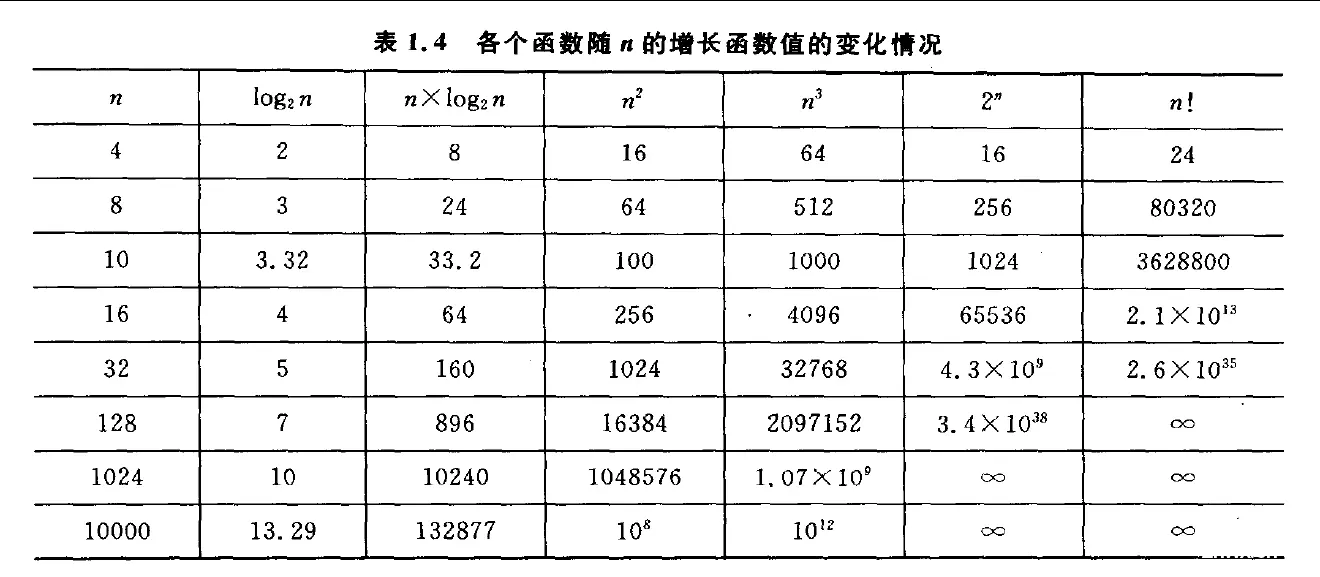
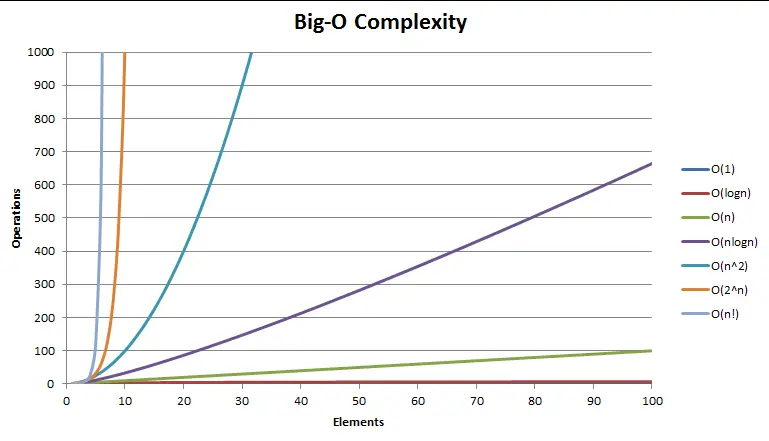
 常见复杂度对比：