目录

1137.第N个泰波那契数

解法（动态规划） 算法流程

1. 状态表⽰：

2. 状态转移⽅程：

3. 初始化：

4. 填表顺序：

5. 返回值：

 C++算法代码 

优化： 滚动数组

测试：

08.01.三步问题

解法（动态规划） 算法思路

1. 状态表⽰

2. 状态转移⽅程

3. 初始化

4. 填表顺序

5. 返回值

代码：

测试

746.使⽤最⼩花费爬楼梯

2. 状态转移⽅程：

3. 初始化：

测试：

 91.解码⽅法

算法思路：

1. 状态表⽰：

2. 状态转移⽅程：

3. 初始化：

代码： 

优化

测试

---

1137.第N个泰波那契数

解法（动态规划） 算法流程

1. 状态表⽰：

这道题可以「根据题⽬的要求」直接定义出状态表⽰：

dp[i] 表⽰：第i 个泰波那契数的值。

2. 状态转移⽅程：

题⽬已经⾮常贴⼼的告诉我们了： 

dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]

3. 初始化：

从我们的递推公式可以看出， dp[i] 在 i = 0 以及i = 1 的时候是没有办法进⾏推导的，因 为dp[-2] 或dp[-1] 不是⼀个有效的数据。

因此我们需要在填表之前，将0, 1, 2 位置的值初始化。题⽬中已经告诉我们dp[0] = 0, dp[1] = dp[2] = 1 。

4. 填表顺序：

毫⽆疑问是「从左往右」。

5. 返回值：

应该返回dp[n] 的值。

 C++算法代码 

使⽤⼀维数组：

class Solution {public: int tribonacci(int n) { //如何填，抄状态转移方程 if(n==0||n==1) return n; vector<int> dp(n+1); dp[0]=0,dp[1]=1,dp[2]=1;//初始化前三个 //left->right for(int i=3;i<=n;i++) dp[i]=dp[i-1]+dp[i-2]+dp[i-3]; //返回 return dp[n]; //核心：从左往右一个个+ }};

优化： 滚动数组

 //之后的背包中，会更加常用：

//滚动数组优化int tribonacci(int n){ if(n==0)return 0; if(n==1||n==2)return 1; int a=0,b=1,c=1,d=0; for(int i=3;i<=n;i++) { d=a+b+c; a=b;b=c;c=d; } return d;}

测试：

08.01.三步问题

解法（动态规划） 算法思路

1. 状态表⽰

这道题可以根据「经验+题⽬要求」直接定义出状态表⽰： dp[i] 表⽰：到达 i 位置时，⼀共有多少种⽅法。

2. 状态转移⽅程

以i位置状态的最近的⼀步，来分情况讨论：

如果 dp[i] 表⽰⼩孩上第i 阶楼梯的所有⽅式，那么它应该等于所有上⼀步的⽅式之和：

i. 上⼀步上⼀级台阶， dp[i] += dp[i - 1] ；ii. 上⼀步上两级台阶， dp[i] += dp[i - 2] ；iii. 上⼀步上三级台阶， dp[i] += dp[i - 3] ；

综上所述， dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3] 。

需要注意的是，这道题⽬说，由于结果可能很⼤，需要对结果取模。

在计算的时候，三个值全部加起来再取模，即(dp[i - 1] + dp[i - 2] + dp[i - 3]) % MOD 是不可取的，同学们可以试验⼀下， n 取题⽬范围内最⼤值时，⽹站会报错signed integer overflow 。

对于这类需要取模的问题，我们每计算⼀次（两个数相加/乘等），都需要取⼀次模。否则，万⼀ 发⽣了溢出，我们的答案就错了。

3. 初始化

从我们的递推公式可以看出， dp[i] 在i = 0, i = 1 以及i = 2 的时候是没有办法进⾏ 推导的，因为dp[-3] dp[-2] 或dp[-1] 不是⼀个有效的数据。

 因此我们需要在填表之前，将1, 2, 3 位置的值初始化。

根据题意， dp[1] = 1, dp[2] = 2, dp[3] = 4 。

4. 填表顺序

毫⽆疑问是「从左往右」。

5. 返回值

应该返回dp[n] 的值。

代码：

#define MOD 1000000007class Solution { //有一点起始累加，到最后一个的感觉public: int waysToStep(int n) { //1.状态表示 i和dp[i]表示什么 //2.方程 dp[i]和最近一步的关系 //3.初始化 不可越界 //4.填表顺序 是从左到右还是从右到左 //5.返回 dp[i/i-1] int i=0; vector<int> dp(n+1);//n+1 因为数组有0 dp[1]=1;dp[2]=2;dp[3]=4; if(n==1||n==2) return n; if(n==3) return 4; for(i=4;i<=n;i++) dp[i]=((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD; return dp[n]; }};

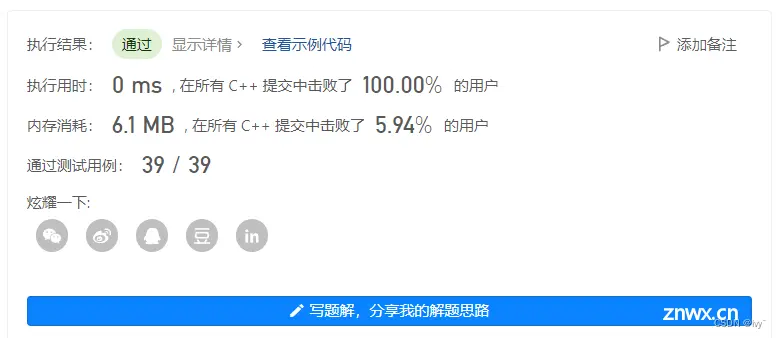
测试

746.使⽤最⼩花费爬楼梯

 

注意注意：

在这道题中，数组内的每⼀个下标[0, n - 1] 表⽰的都是楼层，⽽顶楼的位置其实是在n 的 位置！！！  

之后我们就着重研究：方程和初始化啦~

2. 状态转移⽅程：

根据最近的⼀步，分情况讨论：

▪ 先到达i - 1 的位置，然后⽀付cost[i - 1] ，接下来⾛⼀步⾛到 i 位置：

dp[i - 1] + csot[i - 1] ；

▪ 先到达i - 2 的位置，然后⽀付 cost[i - 2] ，接下来⾛⼀步⾛到i 位置：

dp[i - 2] + csot[i - 2] 。

 dp[i]= min (cost[i-1]+dp[i-1],cost[i-2]+dp[i-2]);

3. 初始化：

从我们的递推公式可以看出，我们需要先初始化i = 0 ，以及i = 1 位置的值。容易得到 dp[0] = dp[1] = 0 ，因为不需要任何花费，就可以直接站在第0 层和第1 层上。

class Solution {public: int minCostClimbingStairs(vector<int>& cost) { int n=cost.size(); //初始化一个dp表 vector<int> dp(n+1,0); //初始化 dp[0]=dp[1]=0; //填表 for(int i=2;i<n+1;i++) //根据状态转移方程得 dp[i]=min(cost[i-1]+dp[i-1],cost[i-2]+dp[i-2]); //一步两步当中，勇敢取小 return dp[n]; }};

测试：

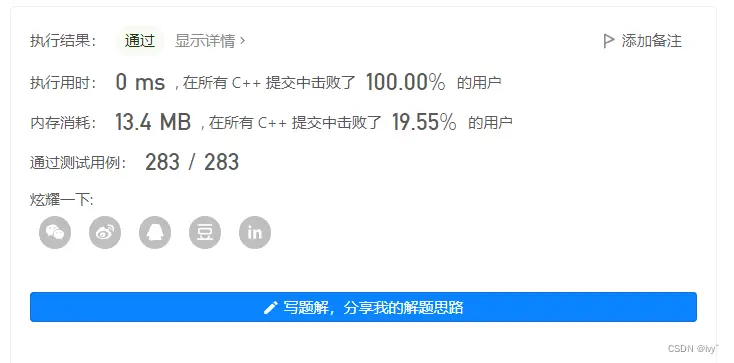
 91.解码⽅法

算法思路：

类似于斐波那契数列~

1. 状态表⽰：

根据以往的经验，对于⼤多数线性dp ，我们经验上都是「以某个位置结束或者开始」做⽂章，这 ⾥我们继续尝试「⽤i位置为结尾」结合「题⽬要求」来定义状态表⽰。

 dp[i] 表⽰：字符串中 [0，i] 区间上，⼀共有多少种编码⽅法。//一般都是所求及dp

2. 状态转移⽅程：

定义好状态表⽰，我们就可以分析 i 位置的 dp 值，如何由「前⾯」或者「后⾯」的信息推导出 来。

关于i 位置的编码状况，我们可以分为下⾯两种情况：

i. 让i 位置上的数单独解码成⼀个字⺟；ii. 让i 位置上的数与i - 1 位置上的数结合，解码成⼀个字⺟。

 下⾯我们就上⾯的两种解码情况，继续分析：

◦ 让i位置上的数单独解码成⼀个字⺟，就存在「解码成功」和「解码失败」两种情况：

i. 解码成功：当 i 位置上的数在 [1, 9] 之间的时候，说明i 位置上的数是可以单独解 码的，那么此时[0, i] 区间上的解码⽅法应该等于 [0, i - 1] 区间上的解码⽅ 法。因为 [0, i - 1] 区间上的所有解码结果，后⾯填上⼀个 i 位置解码后的字⺟就 可以了。此时 dp[i] = dp[i - 1] ； ii. 解码失败：当 i 位置上的数是 0 的时候，说明 i 位置上的数是不能单独解码的，那么 此时 [0, i] 区间上不存在解码⽅法。因为 i 位置如果单独参与解码，但是解码失败 了，那么前⾯做的努⼒就全部⽩费了。此时 dp[i] = 0 。

◦ 让 i 位置上的数与 i - 1 位置上的数结合在⼀起，解码成⼀个字⺟，也存在「解码成功」 和「解码失败」两种情况：

i. 解码成功：当结合的数在[10, 26] 之间的时候，说明[i - 1, i] 两个位置是可以 解码成功的，那么此时[0, i] 区间上的解码⽅法应该等于[0, i - 2 ]区间上的解码 ⽅法，原因同上。此时 dp[i] = dp[i - 2] ；  ii. 解码失败：当结合的数在[0, 9] 和[27 , 99] 之间的时候，说明两个位置结合后解 码失败（这⾥⼀定要注意00 01 02 03 04 ......这⼏种情况），那么此时[0, i] 区 间上的解码⽅法就不存在了，原因依旧同上。此时 dp[i] = 0 。

综上所述： dp[i] 最终的结果应该是上⾯四种情况下，解码成功的两种的累加和（因为我们关⼼ 的是解码⽅法，既然解码失败，就不⽤加⼊到最终结果中去），因此可以得到状态转移⽅程 （ dp[i] 默认初始化为 0 ）：

 i. 当 s[i] 上的数在 [1, 9] 区间上时： dp[i] += dp[i - 1] ； ii. 当 s[i - 1] 与 s[i] 上的数结合后，在[10, 26] 之间的时候： dp[i] += dp[i - 2] ；

如果上述两个判断都不成⽴，说明没有解码⽅法， dp[i] 就是默认值 0 。

3. 初始化：

⽅法⼀（直接初始化）：

由于可能要⽤到i - 1 以及i - 2 位置上的dp 值，因此要先初始化「前两个位置」。初始化dp[0] ：

 i. 当s[0] == '0' 时，没有编码⽅法，结果dp[0] = 0 ；

 ii. 当s[0] != '0' 时，能编码成功， dp[0] = 1

 初始化dp[1] ：

i. 当s[1] 在[1，9] 之间时，能单独编码，此时dp[1] += dp[0] （原因同上， dp[1] 默认为0 ）

ii. 当s[0] 与s[1] 结合后的数在[10, 26] 之间时，说明在前两个字符中，⼜有⼀种 编码⽅式，此时dp[1] += 1

 ⽅法⼆（添加辅助位置初始化）：

可以在最前⾯加上⼀个辅助结点，帮助我们初始化。使⽤这种技巧要注意两个点：

i. 辅助结点⾥⾯的值要保证后续填表是正确的；

ii. 下标的映射关系

代码： 

class Solution { // dp 是一种从起始到末的次数累加public: int numDecodings(string s) { // size int n = s.size(); vector<int> dp(n); // 创建一个dp表 // 初始化前两个位置 dp[0] = s[0] != '0'; if (n == 1) return dp[0]; // 处理边界情况 if (s[1] <= '9' && s[1] >= '1') dp[1] += dp[0]; int t = (s[0] - '0') * 10 + s[1] - '0';//如果和前一个数 联合编码 if (t >= 10 && t <= 26) dp[1] += 1; for (int i = 2; i < n; i++) { // 如果单独编码 if (s[i] <= '9' && s[i] >= '1') dp[i] += dp[i - 1]; int t = (s[i - 1] - '0') * 10 + s[i] - '0'; if (t >= 10 && t <= 26) dp[i] += dp[i - 2]; } return dp[n - 1]; }};

优化

使用添加辅助结点的方式 初始化：

class Solution {public: int numDecodings(string s) { // 优化 int n = s.size(); vector<int> dp(n + 1); dp[0] = 1; // 保证后续填表是正确的 dp[1] = s[0] != '0'; // 填表 for (int i = 2; i <= n; i++) { // 处理单独编码 if (s[i - 1] != '0') dp[i] += dp[i - 1]; // 如果和前⾯的⼀个数联合起来编码 int t = (s[i - 2] - '0') * 10 + s[i - 1] - '0'; if (t >= 10 && t <= 26) dp[i] += dp[i - 2]; } return dp[n]; }};

测试

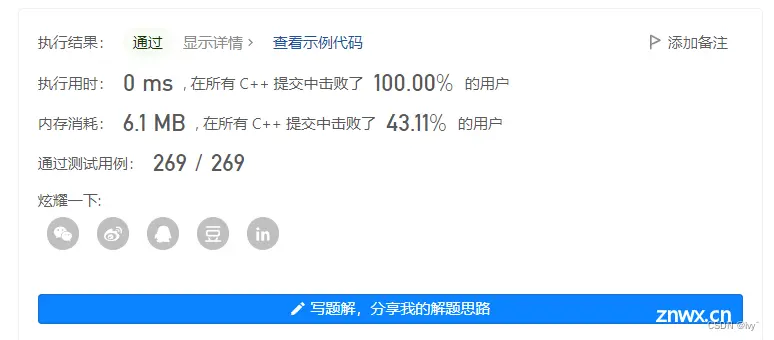
 本文就到这里结束啦，大家也可以多多去力扣刷一些 动态规划的题  巩固一下~