解释DFT是DTFT在频域中均匀采样得到的

首先介绍DTFT和DFT的频谱特点是有所不同的离散时间傅立叶变换 (DTFT)特点

离散傅立叶变换 (DFT)特点

总结频谱泄露与窗口函数应用场景例子信号定义DTFTDFTDFT 作为 DTFT 的采样示例计算信号定义计算 DTFT计算 DTFT 的幅度谱和相位谱计算 DFT绘制幅度谱绘制相位谱

首先介绍DTFT和DFT的频谱特点是有所不同的

离散时间傅立叶变换 (DTFT) 和离散傅立叶变换 (DFT) 的频谱特点有所不同，这些特点主要体现在频谱的周期性、连续性和采样等方面。下面是它们各自频谱特点的对比：

离散时间傅立叶变换 (DTFT)

特点

周期性:

DTFT 的频谱是周期的，对所有整数。这种周期性来源于指数函数的周期性。

连续性:

DTFT 的频谱是一个连续函数，定义在 (-\pi) 到 (\pi) 或 (0) 到 (2\pi) 的区间内。频谱函数 是关于 的连续函数，这意味着它可以取任何值在这个区间内。

无限长信号:

DTFT 适用于无限长度的离散时间信号。因此，它可以给出信号完整的频谱特性。

离散傅立叶变换 (DFT)

特点

周期性:

DFT 的频谱 (X[k]) 本质上是 DTFT 频谱在 ([0, 2\pi)) 区间内的均匀采样，DFT 的频谱也是周期性的，周期为 (N)，其中 (N) 是信号的长度。

离散性:

DFT 的频谱是一个离散函数，定义在 (0) 到 (N-1) 的整数索引上。频谱函数 (X[k]) 是关于 (k) 的离散函数，这意味着它只在 (k = 0, 1, N-1） 上有定义。

有限长度信号:

DFT 适用于有限长度的离散时间信号。它通常用于分析信号的一个片段，这个片段被视为周期信号的一个周期。

总结

DTFT 的频谱是连续的、周期为 (2\pi) 的函数，适用于无限长度的信号。DFT 的频谱是离散的、周期为 (N) 的函数，适用于有限长度的信号。

频谱泄露与窗口函数

频谱泄露:

当使用 DFT 分析非周期信号时，由于信号在时域中的截断，会导致频谱泄露现象。频谱泄露是指信号的真实频谱与 DFT 所得到的频谱之间存在的差异，特别是在频率分量的旁瓣出现额外的能量分布。

窗口函数:

为了减少频谱泄露的影响，通常在信号两端应用窗口函数（如汉明窗、海明窗、布莱克曼窗等）。窗口函数可以平滑信号的边缘，减少突然开始和结束所导致的频谱泄露。

应用场景

DTFT 适用于理论分析和无限长度信号的频谱分析。DFT 适用于实际应用中的信号处理和频谱分析，特别是有限长度信号的分析，如音频信号处理、图像处理等。

通过以上对比，我们可以看到 DTFT 和 DFT 在频谱特点上的明显差异，这些差异决定了它们在不同应用场景中的适用性。

让我们通过一个具体的例子来说明如何从 DTFT 得到 DFT，以及为什么 DFT 可以被认为是 DTFT 在频域中的均匀采样。

例子

假设我们有一个非周期但离散时间的信号 (x[n])，长度为 (N = 8)，我们想要计算这个信号的 DFT 和 DTFT，并观察两者之间的关系。

信号定义

假设信号 (x[n]) 如下：

这是一个简单的矩形脉冲信号，长度为 8 个样本。

DTFT

首先，我们计算信号N=8，矩形序列 的 DTFT，

我们可以写出 DTFT 的表达式，

这是一个几何级数，我们可以求出它的和

DFT

接下来，我们计算信号 (x[n]) 的 DFT，对于 (k = 0, 1, \ldots, 7)：

对于 (0 \leq n < 8)，我们可以写出 DFT 的表达式：

这个表达式与 DTFT 的表达式类似，只是 (k) 的取值范围是有限的，是从0到7

DFT 作为 DTFT 的采样

我们可以看到，DFT 的频谱 是 DTFT 频谱在 ([0, 2\pi)) 区间内的均匀采样。具体来说，

示例计算

<code>

```bash

import numpy as np

import matplotlib.pyplot as plt

# 信号定义

N = 8

n = np.arange(N)

x = np.ones(N)

# 计算 DTFT

def dtft(x, omega):

return np.sum(x * np.exp(-1j * omega * n))

# 创建频率向量

omega = np.linspace(-np.pi, np.pi, 1000) # 用于绘制 DTFT

# 计算 DTFT 的幅度谱和相位谱

X_dtft = np.array([dtft(x, w) for w in omega])

magnitude_dtft = np.abs(X_dtft)

phase_dtft = np.angle(X_dtft)

# 计算 DFT

X_dft = np.fft.fft(x)

magnitude_dft = np.abs(X_dft)

phase_dft = np.angle(X_dft)

# 绘制幅度谱

plt.figure(figsize=(12, 6))

plt.subplot(2, 2, 1)

plt.plot(omega, magnitude_dtft)

plt.title('Magnitude Spectrum of DTFT')

plt.xlabel('Frequency (radians)')

plt.ylabel('Magnitude')

plt.subplot(2, 2, 2)

plt.stem(np.arange(N), magnitude_dft)

plt.title('Magnitude Spectrum of DFT')

plt.xlabel('Frequency Index')

plt.ylabel('Magnitude')

# 绘制相位谱

plt.subplot(2, 2, 3)

plt.plot(omega, phase_dtft)

plt.title('Phase Spectrum of DTFT')

plt.xlabel('Frequency (radians)')

plt.ylabel('Phase (radians)')

plt.subplot(2, 2, 4)

plt.stem(np.arange(N), phase_dft)

plt.title('Phase Spectrum of DFT')

plt.xlabel('Frequency Index')

plt.ylabel('Phase (radians)')

plt.tight_layout()

plt.show()

图片结果展示

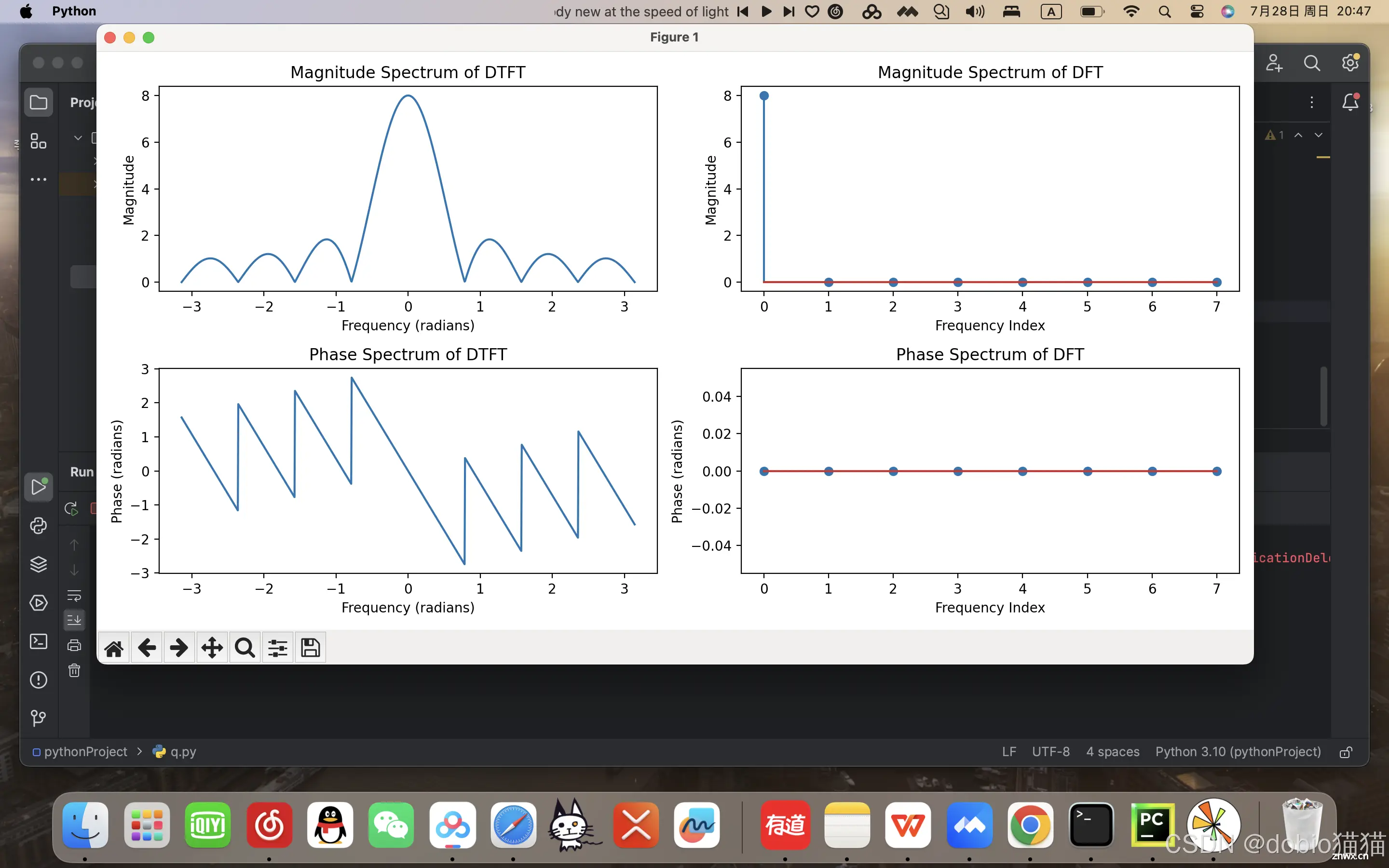
这段代码是用来展示一个长度为8个样本的离散时间信号（全1序列）的离散时间傅立叶变换（DTFT）和离散傅立叶变换（DFT）的幅度谱和相位谱的。下面是对每个部分的解释：

信号定义

<code>N = 8: 信号长度为8个样本。n = np.arange(N): 时间索引从0到N-1。x = np.ones(N): 信号x[n]是一个全1序列。

计算 DTFT

定义了一个函数 dtft(x, omega) 来计算给定信号x在频率omega处的DTFT值。omega 是一个从-(\pi) 到 (\pi) 的频率向量，用于计算和绘制DTFT。

计算 DTFT 的幅度谱和相位谱

使用列表推导式来计算omega范围内所有频率点上的DTFT值，并存储在 X_dtft 中。magnitude_dtft = np.abs(X_dtft) 和 phase_dtft = np.angle(X_dtft) 分别计算DTFT的幅度和相位。

计算 DFT

使用 np.fft.fft(x) 来计算信号x的DFT。magnitude_dft = np.abs(X_dft) 和 phase_dft = np.angle(X_dft) 分别计算DFT的幅度和相位。

绘制幅度谱

第一个子图显示了DTFT的幅度谱，频率范围从-(\pi) 到 (\pi)。第二个子图使用茎状图显示了DFT的幅度谱，频率索引从0到N-1。

绘制相位谱

第三个子图显示了DTFT的相位谱，频率范围从-(\pi) 到 (\pi)。第四个子图使用茎状图显示了DFT的相位谱，频率索引从0到N-1。

由于这是一个全1序列，我们可以预期以下特性：

幅度谱：对于DTFT来说，会形成一个矩形窗函数的sinc函数形状。对于DFT，由于信号是周期性的，我们期望在0频率处有一个峰值，表示信号的直流分量，其余频率分量均为0。相位谱：对于全1序列，由于信号没有相移，因此相位谱应该是0或者未定义（因为正弦波的幅度为0时相位无意义）。

让我们根据这些描述来可视化结果。由于无法直接运行代码，我们可以想象这些图像的样子并基于上述理论解释它们。

幅度谱应该显示出一个在0频率处的峰值，对于DTFT，它将在(-\pi)到(\pi)的频率轴上平滑变化；对于DFT，它将在第0个频率指数上有一个尖峰。相位谱应该接近于0，除了那些幅度为0的点，其相位可能是未定义的或数值噪声导致的小数值。

对于一个全1序列（即每个元素都是1的序列），其离散傅立叶变换（DFT）会在0频率处有一个尖峰，这是因为该序列代表了一个恒定的直流信号（DC component）。在频域中，直流信号对应于频率为0的情况，即信号的平均值或常数项。

在数学上，DFT在k次频率分量的定义是：

[ X[k] = \sum_{n=0}^{N-1} x[n] e^{-j2\pi kn/N} ]

其中:

( N ) 是序列的长度。( x[n] ) 是时间域中的信号。( X[k] ) 是频率域中的信号。( k ) 是频率索引，范围从 0 到 ( N-1 )。( n ) 是时间索引，范围从 0 到 ( N-1 )。

当信号 ( x[n] ) 是一个全1序列时，即 ( x[n] = 1 ) 对所有的 ( n )，我们可以计算DFT的各频率分量。

在这个情况下，指数项不再是1，而是一个旋转因子，其值在复平面上绕着单位圆旋转。对于任何非零的 ( k )，这个旋转因子会导致正弦和余弦的和最终抵消，从而使得 ( X[k] ) 的值为0。

总结起来，对于一个全1序列：

在 ( k = 0 ) 处，DFT的值为 ( N )，因为这是信号的直流分量，也是信号的总能量。在 ( k > 0 ) 处，DFT的值为 0，因为旋转因子导致了正弦和余弦的和相互抵消。

这解释了为什么对于一个全1序列，DFT只在0频率处有一个尖峰，而在其他频率处都是0。这个尖峰的大小等于序列的长度 ( N )。