离散傅里叶变换（DFT）和快速傅里叶变换（FFT）是信号处理和数字信号处理中的基本工具。它们用于将时间域的信号转换为频率域的表示，帮助分析信号的频谱成分。

1. 离散傅里叶变换（DFT）

1.1 DFT的基本概念

DFT是将离散时间信号转换为频域表示的工具。对于长度为 N 的离散信号 x[n]，其DFT定义为：

其中：

X[k] 是频域信号的第

𝑘k 个频率分量

x[n] 是时间域信号的第

n 个样本

N 是信号的总样本数

j 是虚数单位

1.2 逆DFT（IDFT）

逆DFT用于将频域信号转换回时间域信号：

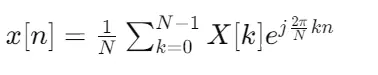
1.3 DFT的性质

2. 快速傅里叶变换（FFT）

2.1 FFT的基本概念

2.2 Cooley-Tukey算法

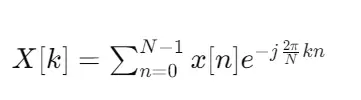
通过递归地应用这种分解，可以大幅减少计算量。

2.3 FFT的实现

以下是Python中使用NumPy库实现DFT和FFT的示例代码：

<code>import numpy as np

import matplotlib.pyplot as plt

# 生成一个示例信号

N = 1024

t = np.linspace(0, 1, N)

f1, f2 = 50, 120

x = np.sin(2 * np.pi * f1 * t) + 0.5 * np.sin(2 * np.pi * f2 * t)

# DFT的实现

def dft(x):

N = len(x)

X = np.zeros(N, dtype=complex)

for k in range(N):

for n in range(N):

X[k] += x[n] * np.exp(-2j * np.pi * k * n / N)

return X

# 计算DFT

X_dft = dft(x)

# 使用NumPy的FFT计算

X_fft = np.fft.fft(x)

# 绘制结果

frequencies = np.fft.fftfreq(N)

plt.figure(figsize=(12, 6))

# DFT

plt.subplot(2, 1, 1)

plt.plot(frequencies[:N//2], np.abs(X_dft)[:N//2])

plt.title('DFT')

plt.xlabel('Frequency (Hz)')

plt.ylabel('Magnitude')

# FFT

plt.subplot(2, 1, 2)

plt.plot(frequencies[:N//2], np.abs(X_fft)[:N//2])

plt.title('FFT')

plt.xlabel('Frequency (Hz)')

plt.ylabel('Magnitude')

plt.tight_layout()

plt.show()

2.4 FFT的应用

频谱分析： 用于分析信号的频率成分。

滤波器设计： 快速设计和实现数字滤波器。

卷积计算： 利用FFT快速计算大规模卷积。

音频处理： 如音频压缩、增强和特效。