写在前面：

🌟 欢迎光临 清流君 的博客小天地，这里是我分享技术与心得的温馨角落。📝

个人主页：清流君_CSDN博客，期待与您一同探索 移动机器人 领域的无限可能。

🔍 本文系 清流君 原创之作，荣幸在CSDN首发🐒

若您觉得内容有价值，还请评论告知一声，以便更多人受益。

转载请注明出处，尊重原创，从我做起。

👍 点赞、评论、收藏，三连走一波，让我们一起养成好习惯😜

在这里，您将收获的不只是技术干货，还有思维的火花！

📚 系列专栏：【运动控制】系列，带您深入浅出，领略控制之美。🖊

愿我的分享能为您带来启迪，如有不足，敬请指正，让我们共同学习，交流进步！

🎭 人生如戏，我们并非能选择舞台和剧本，但我们可以选择如何演绎 🌟

感谢您的支持与关注，让我们一起在知识的海洋中砥砺前行~~~

---

文章目录

引言一、MPC主流求解器二、MPC加速1、减少模型阶数2、缩短预测时长3、减少约束4、降低精确度要求

三、显式模型预测控制 (Explicit MPC)1、显示MPC的核心思想2、举例说明

四、大规模问题的分类讨论1、等式约束2、不等式约束

五、KKT条件1、对 z 求导等于02、互补松弛条件3、对偶可行性条件4、主问题可行性条件

六、显式MPC的缺陷七、MPC优缺点总结1、MPC的优点a）控制器公式直观b）状态和控制信号的安全范围c）适合车辆控制d）适用于各种类型的系统

2、MPC的缺点a）计算量较大b）可能不稳定或无法求得可行解

参考资料

引言

本篇博客将介绍MPC的求解器及如何加速MPC的运算。

---

一、MPC主流求解器

MPC可以根据不同情况采用不同求解方法：

对于线性无约束的情况，直接使用解析解，通过 动态规划(DP) 求解。对于线性有约束的情况，将其转化为 二次规划(QP) 求解。

MPC有许多流行的求解器，包括商用的和开源的。以下是一些常用求解器：

Software	Year	Target	License
ACADO Codegen	2009	NMPC	LGPL v3
qpOASES	2006	QP	LGPL v2.1
FORES	2011	QP, QCQP	proprietary
FORES NLP	2017	NMPC	proprietary
OSQP	2017	QP	Apache v2.0
acados	2018	NMPC	2-clause BSD

对于线性MPC：qpOASES、FORCES 和 OSQP都是很好用的求解器，能够有效解决具有约束的线性MPC问题。对于非线性MPC：同样有多种求解器可供选择，例如 ACADO Codegen 、acados、FORES NLP，这些都是开源的求解器，适用于求解具有非线性约束的MPC问题。

---

二、MPC加速

接下来，我们将讨论一个实际问题：如何提高MPC的计算速度？

根据之前对MPC理论部分的介绍，可以把 MPC 变成 QP 问题：

min

⁡

z

1

2

z

T

H

z

+

x

0

T

F

z

s

.

t

.

     

G

z

≤

W

+

s

x

0

\min_{\mathbf{z}}\quad\frac{1}{2}\mathbf{z}^{T}\mathbf{H}\mathbf{z}+{x}_{0}^{T}\mathbf{F}\mathbf{z}\\\mathrm{s.t.}\ \ \ \ \ G\mathbf{z}\leq W+s{x}_{0}

zmin​21​zTHz+x0T​Fzs.t.     Gz≤W+sx0​ 解决一个 二次规划(QP) 问题，其复杂度会随着状态量、约束量以及预测时长的增加而增加。因此，随着这些参数的增多，问题的复杂度也会相应提高。

在自动驾驶领域，对车辆控制的需求是实时且迅速的，这意味着采样时间通常非常短，例如毫秒级别。但是芯片的内存和算力有限，为了减少MPC的计算量并提高其运行速度，我们可以采取以下几种方法：

1、减少模型阶数

简化模型是提高MPC计算速度的一种有效方法，通过减少模型的阶数，去除一些对系统行为影响较小的状态参数，可以显著降低计算复杂度，从而加快问题求解的速度。

这种简化可以基于对系统动态特性的深刻理解和对控制目标的精确把握来实现。

2、缩短预测时长

减少对未来时间的预测步数，只关注较近的未来，而不是长时间范围。

预测时长的选择与问题的复杂程度有关，因为较短的预测时长会减少需要考虑的状态和约束数量，从而降低计算复杂度。

3、减少约束

约束的增加会导致问题的复杂度增加，因为每个约束都需要在优化过程中被考虑和满足。通过精简约束条件，可以简化优化问题，从而提高MPC的计算速度。

这通常涉及到对约束的优先级进行评估，并确定哪些约束对系统性能的影响最小，可以被移除或放宽。

4、降低精确度要求

在MPC中，通常寻求一个精确的解来确保系统的性能。但如果对解的精确度要求不那么严格，可以使用更快的算法或更简化的模型来近似解。

在实际应用中，这意味着我们可以接受一个稍微不那么精确但足够好的解，而不是追求一个完美的解。这种方法在计算资源有限的情况下尤其有用，因为它可以在保证系统性能的前提下，提高MPC的计算效率。

---

三、显式模型预测控制 (Explicit MPC)

那么有没有更系统化的方法来使 MPC 跑得更快？其实也是有的，就是 显式MPC (Explicit MPC).

下面我们就对 Explicit MPC进行深入的了解。

1、显示MPC的核心思想

Explicit MPC之所以能够加快求解进程，主要是因为它将一部分优化问题从在线(online) 处理，转变为了 离线 (offline) 处理。在传统的MPC中，优化问题通常在预测时域的初始阶段一次性求解，然后在线阶段根据实际状态和约束条件执行预先计算的控制序列。

而在Explicit MPC中，优化问题在每个采样时刻都进行离线求解，这意味着在实际运行之前，所有可能的状态和控制输入组合都已经经过优化处理。这种离线优化可以利用更强大的计算资源，如高性能计算机或专用硬件，以获得更精确的解。一旦优化完成，在线阶段只需根据当前状态执行计算出的控制输入，从而减少了在线计算的负担。

因此，Explicit MPC通过将部分计算任务转移到离线阶段，实现了对在线计算速度的提升，尤其是在预测时域较长或问题规模较大的情况下。这种方法提高了MPC系统的实时性能，使其能够更有效地处理复杂的控制问题。

举个例子，这个就像我们煲汤的过程。如果从原始的原料开始煲汤，这个过程可能需要很长时间。但如果事先准备了一个已经大致做好的汤底，那么只需将这个汤底加入，就能更容易地煲出一锅美味的汤。

因此，显性MPC（Explicit MPC）的思路是预先为不同的初始状态区间计算好相应的二次规划（QP）问题，然后在实际应用中，只需根据当前的初始状态去查询这个预先计算好的表格，即可得到相应的最优控制序列。

2、举例说明

下面通过一个例子来学习 显性MPC，假设有一个一维的二次规划问题：

J

∗

(

x

)

=

min

⁡

z

J

(

z

,

x

)

=

1

2

z

2

s

.

t

.

   

z

≤

1

+

3

x

\begin{aligned}J^{*}(x)&=\min_{z}J(z,x)=\frac{1}{2}z^{2}\\\mathrm{s.t.}\ \ \ &z\leq1+3x\end{aligned}

J∗(x)s.t.   ​=zmin​J(z,x)=21​z2z≤1+3x​决策变量是

z

z

z，注意这里的

x

x

x 并不是决策变量，而是一个参数。

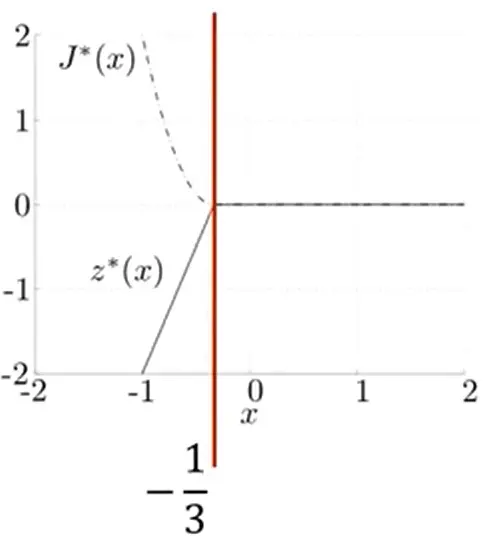
如果没有约束条件

z

≤

1

+

3

x

z \le 1+3x

z≤1+3x ，那么二次函数的极值点是在

z

=

0

z = 0

z=0 处，引入了这个约束，就需要分情况讨论：

若

x

>

−

1

3

x >-\frac{1}{ 3}

x>−31​，即约束

z

≤

z \le

z≤ 一个正数，那么

z

z

z 可以取极值点

0

0

0。此时函数的最小值就是极小值，即

z

=

0

z = 0

z=0 时 ， 目标函数

J

∗

=

0

J^*=0

J∗=0 。

x

≤

−

1

3

x \le-\frac{1}{ 3}

x≤−31​ 时，

z

z

z 就取不到极值点

0

0

0 了，而只能取边界上的一个点。在这种情况下，函数的最小值在

z

=

1

+

3

x

z = 1 + 3x

z=1+3x 处取得，函数的最小值需要分两段来讨论。

这个例子表明，只需要一些基础的数学知识，就可以理解约束条件如何影响二次函数的极值。

---

四、大规模问题的分类讨论

对于大规模的问题，要如何分类讨论呢？

1、等式约束

对于等式约束求极值的问题，可以使用拉格朗日乘子算法。这个方法是将约束条件乘以一个拉格朗日乘子（通常表示为

λ

λ

λ），然后将其加到目标函数中，形成一个拉格朗日函数。然后对这个拉格朗日函数分别对

z

z

z 和

λ

λ

λ 求导，并将导数设为零，分别求极值。

2、不等式约束

然而，对于不等式约束问题，情况就没有那么简单了。在这种情况下，我们需要使用到著名的KKT(Karush-Kuhn-Tucker) 条件。KKT条件是一组包含原始目标函数、约束条件以及拉格朗日乘子的一些必要条件，它们一起定义了问题是否有可行解，以及这个解是否是最优的。

---

五、KKT条件

对于不等式约束问题，KKT条件包括以下四类方程：

1、对 z 求导等于0

z

+

λ

=

0

z+\lambda=0

z+λ=0这表示在极值点处，目标函数关于

z

z

z 的偏导数为零。

2、互补松弛条件

λ

(

z

−

3

x

−

1

)

=

0

\lambda(z-3x-1)=0

λ(z−3x−1)=0核心公式，要么

λ

=

0

\lambda=0

λ=0，要么

g

(

z

)

=

0

g(z)=0

g(z)=0，此处要求两者不能同时为

0

0

0 。

3、对偶可行性条件

λ

≥

0

\lambda \ge 0

λ≥0要求拉格朗日乘子必须为正。

4、主问题可行性条件

z

−

3

x

−

1

≤

0

z-3x-1\leq0

z−3x−1≤0就是原问题的约束。

KKT条件是凸优化中一个非常重要的知识点。如果大家对此感兴趣，可以参考以下链接深入了解一下。在这里仅将其作为结论来使用。

Karush-Kuhn-Tucker（KKT）条件

因此，我们可以证明，对于一个严格的凸优化问题，即二次规划（QP）问题，多参数规划的解实际上是分段线性的。这意味着对于显性MPC，我们可以一开始就计算好一部分优化问题。

例如下面这个优化问题：

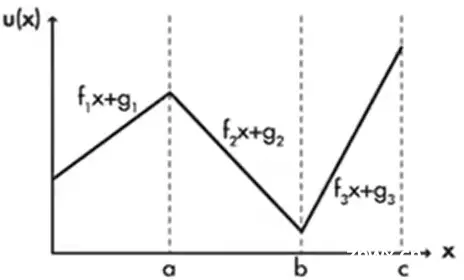
可以把它变成分段函数：

u

(

x

)

=

{

f

1

x

+

g

1

   

i

f

   

0

<

x

<

a

f

2

x

+

g

2

   

i

f

   

a

<

=

x

<

b

f

3

x

+

g

3

   

i

f

   

b

<

=

x

<

=

c

\left.u(x)=\left\{\begin{array}{ll}{ {f_{1}x+g_{1} \ \ \ \mathrm{if} \ \ \ 0<x<a}}\\{ {f_{2}x+g_{2}\ \ \ \mathrm{if} \ \ \ a<=x<b}}\\{ {f_{3}x+g_{3}\ \ \ \mathrm{if}\ \ \ b<=x<=c}}\\\end{array}\right.\right.

u(x)=⎩

⎨

⎧​f1​x+g1​   if   0<x<af2​x+g2​   if   a<=x<bf3​x+g3​   if   b<=x<=c​

在不同的时间段有不同的表达式，由此得到在线计算的这步：

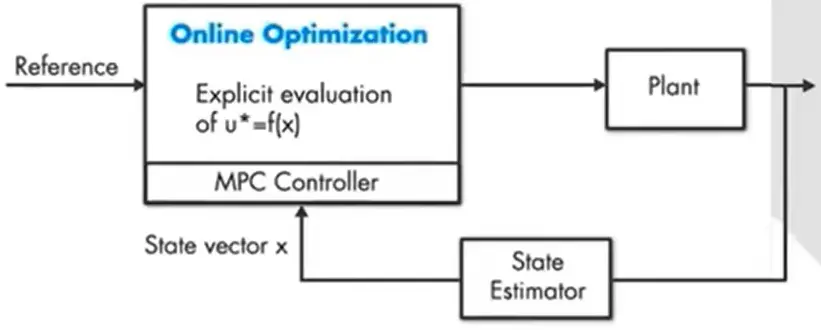
此时可根据不同时期直接查表，速度会变得快很多。

---

六、显式MPC的缺陷

显性MPC看起来是一个非常理想的选择，只需在离线时计算好初始状态

x

0

x_0

x0​的不同区间，以及每个区间对应的最优解，执行时只需查表即可。

但实际上存在一个问题，即区间的数量和有限约束的数量呈指数增长。当问题规模较大时，存储如此多的区间会消耗大量内存。即使是在执行时查表，也变成了一件相对耗时的事情。

这就是为什么显性MPC大多应用于自动化控制领域，而在机器人领域很少应用的原因。

---

七、MPC优缺点总结

1、MPC的优点

最后，我们来总结一下MPC的特点和优势。MPC的优点非常明显：

a）控制器公式直观

MPC需要定义目标函数、相关约束，并基于模型预测未来的状态，然后对这些预测进行优化。它使用成熟的求解器来解决优化问题。

b）状态和控制信号的安全范围

MPC可以将状态和控制信号限制在一个安全的范围内，并且可以选择同时最大化多个目标。它还允许使用软约束和硬约束以及软惩罚，为控制约束问题提供了丰富的解决方案。

c）适合车辆控制

由于车辆系统中存在许多执行器约束和不同的性能目标，MPC非常适合用于车辆的控制。

d）适用于各种类型的系统

MPC不仅适用于线性系统，也适用于非线性的技术系统。这意味着，即使模型随时间变化或改进，我们仍然可以使用相同的方法进行优化。

2、MPC的缺点

然而，MPC的缺点也是显而易见的：

a）计算量较大

MPC的计算时间通常比静态、离线控制算法需要更多的计算资源。为了减少处理器过载的问题，我们可以优化公式或算法。

b）可能不稳定或无法求得可行解

在某些情况下，MPC可能无法稳定运行或无法找到一个可行的解。这些问题可以通过具体问题的分析和调整来解决。

综上所述，MPC通过其直观的控制器公式、安全的状态和控制信号范围以及丰富的解决方案，为车辆控制提供了一个强大的工具。但MPC的计算需求和潜在的不稳定性是需要注意的问题，这些问题可以通过适当的方法有效解决。

---

参考资料

自动驾驶规划控制

---

后记：

🌟 感谢您耐心阅读这篇关于 主流求解器及MPC加速 的技术博客。 📚

🎯 如果您觉得这篇博客对您有所帮助，请不要吝啬您的点赞和评论 📢

🌟您的支持是我继续创作的动力。同时，别忘了收藏本篇博客，以便日后随时查阅。🚀

🚗 让我们一起期待更多的技术分享，共同探索移动机器人的无限可能！💡

🎭感谢您的支持与关注，让我们一起在知识的海洋中砥砺前行 🚀