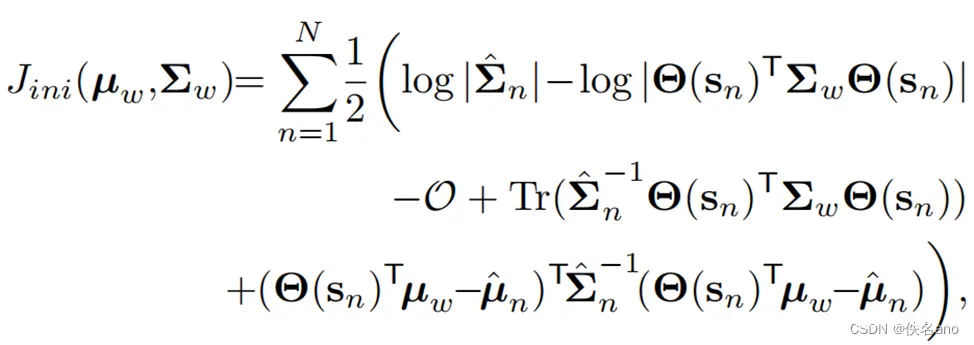KMP-一种用于生成和优化运动轨迹的方法-人工智能及其应用-课程学习记录-2
佚名ano 2024-07-18 10:31:02 阅读 73
Kernelised Movement Primitives (KMP) 是一种用于生成和优化运动轨迹的方法,它基于运动轨迹的轨迹基元(Movement Primitives, MP)概念。KMP 利用核方法(Kernel Methods)和概率统计工具来实现运动轨迹的生成、泛化和适应。这种方法在机器人学和运动控制领域特别有用,能够处理复杂的运动任务,并在不同的环境和约束条件下进行轨迹调整和优化。
KMP的基本概念
运动基元(Movement Primitives, MP):
运动基元是描述机器人或运动系统的基本运动单元,能够被组合和调整以实现复杂的运动任务。MP 通常用参数化的方式表示,能够被学习和再现。
核方法(Kernel Methods):
核方法是一类机器学习算法,利用核函数(Kernel Functions)将数据映射到高维特征空间,从而在该空间中进行线性操作。在KMP中,核方法用于处理和泛化运动基元。
KMP的基本步骤
数据收集:
收集用于训练的运动数据,可以是示范数据或通过模拟生成的数据。这些数据通常包括时间、位置、速度和加速度等。
轨迹建模:
使用核方法和高斯过程回归(Gaussian Process Regression, GPR)对收集的运动数据进行建模。建立运动基元的概率模型,能够描述轨迹的不确定性和变化范围。
轨迹生成:
给定初始条件和目标条件,利用核方法生成符合要求的轨迹。通过调整核函数和参数,能够生成多种变化形式的轨迹,以适应不同的任务要求。
轨迹优化:
根据实际环境和约束条件,对生成的轨迹进行优化。可以利用最优化算法或约束满足问题(Constraint Satisfaction Problem, CSP)解决轨迹优化问题。
KMP的优势
灵活性:
KMP能够适应多种运动任务和环境变化,通过调整核函数和参数,可以生成多种形式的轨迹。
泛化能力:
利用概率模型,KMP能够对运动轨迹进行泛化,生成未见过的轨迹,具有良好的泛化能力。
适应性:
KMP能够根据环境和任务要求,对轨迹进行实时调整和优化,提高了运动控制的适应性。
KMP的应用
机器人运动控制:
在机器人学中,KMP用于生成和优化机器人臂的运动轨迹,实现精确的抓取和放置任务。人机交互:
在人机交互领域,KMP用于生成自然的运动轨迹,提高了机器人和人类的交互体验。运动仿真:
在运动仿真和虚拟现实中,KMP用于生成逼真的运动轨迹,提高了仿真效果和用户体验。
以下是一个简单的KMP实现示例,使用Python和scikit-learn库中的高斯过程回归(GPR)来建模和生成轨迹:
<code>import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C
# 生成示范数据
def generate_demo_data(num_points=50):
t = np.linspace(0, 1, num_points)
y = np.sin(2 * np.pi * t)
return t, y
# KMP建模和生成轨迹
def kmp(t_demo, y_demo, t_new):
kernel = C(1.0, (1e-4, 1e1)) * RBF(1, (1e-4, 1e1))
gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10)
gp.fit(t_demo.reshape(-1, 1), y_demo)
y_pred, sigma = gp.predict(t_new.reshape(-1, 1), return_std=True)
return y_pred, sigma
# 主函数
if __name__ == '__main__':
# 生成示范数据
t_demo, y_demo = generate_demo_data()
# 新的时间点
t_new = np.linspace(0, 1, 100)
# KMP生成轨迹
y_pred, sigma = kmp(t_demo, y_demo, t_new)
# 可视化
plt.figure()
plt.plot(t_demo, y_demo, 'r.', markersize=10, label='Training Data')code>
plt.plot(t_new, y_pred, 'b-', label='Predicted Mean')code>
plt.fill_between(t_new, y_pred - 1.96 * sigma, y_pred + 1.96 * sigma, alpha=0.2, color='blue', label='95% Confidence Interval')code>
plt.xlabel('Time')
plt.ylabel('Position')
plt.legend()
plt.show()
以上内容均是查询得到的概念,接下来详细介绍一下KMP算法是个什么玩意
什么是KMP?
KMP (Kernelised Movement Primitives) 是一种生成和优化运动轨迹的方法。想象一下,你要让一个机器人手臂从一点移动到另一点,同时避开障碍物。KMP就像一个聪明的导航系统,可以根据已经学到的示范动作生成平滑且安全的轨迹,这就是KMP的作用.由名字看来,可以理解为一种基于核的方法的运动基元,那么什么又是核方法什么又是运动基元呢?
关键概念
核方法 (Kernel Methods)
核方法是一种数学工具,用来处理复杂的非线性数据.通过核函数,我们可以把数据映射到一个高维空间,在这个高维空间中,我们可以更容易地找到数据之间的关系.而核函数(Kernel Function)是一种数学工具,用来计算数据点之间的相似性. 通过核函数,我们可以在一个高维空间中处理原本在低维空间中难以处理的非线性问题.
假设我们有一堆苹果和橙子,想要把它们分类. 在二维空间中,我们使用两个特征来描述它们:颜色(从红到橙)和重量.
低维空间中的问题:在二维空间中,有些苹果和橙子的颜色和重量很接近,比如,一个非常重的橙子可能看起来像一个苹果,一个颜色非常浅的苹果可能看起来像一个橙子. 这样,我们很难通过简单的线性分割线来区分它们.高维空间中的解决方案:如果我们把这些特征映射到一个更高的维度,比如三维空间(添加一个新的特征,比如形状),在这个高维空间中,这些数据点之间的关系可能变得更加清晰. 比如,所有的苹果在三维空间中可能会聚集在一起,而所有的橙子会聚集在另一个地方. 在高维空间中,我们可以很容易地找到一个平面来分割苹果和橙子.
如下图中,如果只看两维数据,我们会发现无法用线性回归实现分类的目的
但是如果添加一个合理的维度,却有可能实现线性回归
核函数就像一个魔法工具,可以帮助我们计算数据点在高维空间中的相似性,而不需要显式地去计算这些高维空间中的特征. 这样,我们可以在原始的低维空间中处理复杂的非线性问题.
核函数的选择非常重要, 常用的核函数有以下几种:
线性核 (Linear Kernel)
k
(
x
,
x
′
)
=
x
⋅
x
′
k(x,x^{'})=x\cdot x^{'}
k(x,x′)=x⋅x′多项式核 (Polynomial Kernel):
k
(
x
,
x
′
)
=
(
α
x
⋅
x
′
+
c
)
d
k(x,x^{'})=(\alpha x\cdot x^{'}+c)^d
k(x,x′)=(αx⋅x′+c)d径向基函数核 (RBF Kernel) / 高斯核 (Gaussian Kernel):
k
(
x
,
x
′
)
=
exp
(
−
∣
∣
x
−
x
′
∣
∣
2
2
σ
2
)
k(x,x^{'})=\exp(-\frac{||x-x^{'}||^2}{2\sigma^2})
k(x,x′)=exp(−2σ2∣∣x−x′∣∣2)Sigmoid核 (Sigmoid Kernel):
k
(
x
,
x
′
)
=
tanh
(
α
x
⋅
x
′
+
c
)
k(x,x^{'})=\tanh(\alpha x\cdot x^{'}+c)
k(x,x′)=tanh(αx⋅x′+c)
让我们以径向基函数核(RBF核)为例子,RBF核的公式是:
k
(
x
,
x
′
)
=
exp
(
−
∣
∣
x
−
x
′
∣
∣
2
2
σ
2
)
k(x,x^{'})=\exp(-\frac{||x-x^{'}||^2}{2\sigma^2})
k(x,x′)=exp(−2σ2∣∣x−x′∣∣2)
其中:
x
和
x
′
是两个数据点
x和x^{'}是两个数据点
x和x′是两个数据点
∣
∣
x
−
x
′
∣
∣
2
是这两个点之间的欧几里得距离
||x-x^{'}||^2是这两个点之间的欧几里得距离
∣∣x−x′∣∣2是这两个点之间的欧几里得距离
σ
是一个参数,控制相似性衰减的速度
\sigma 是一个参数,控制相似性衰减的速度
σ是一个参数,控制相似性衰减的速度
这个核函数的作用是:当两个数据点
x
和
x
′
非常接近时,它们的距离
∣
∣
x
−
x
′
∣
∣
2
很小
这个核函数的作用是:当两个数据点x和x^{'}非常接近时,它们的距离||x-x^{'}||^2很小
这个核函数的作用是:当两个数据点x和x′非常接近时,它们的距离∣∣x−x′∣∣2很小
核函数值
k
(
x
,
x
′
)
接近
1.
当两个数据点
x
和
x
′
距离很远时,核函数值核函数值
k
(
x
,
x
′
)
接近
0
核函数值k(x,x^{'})接近 1. 当两个数据点x和x^{'}距离很远时,核函数值核函数值k(x,x^{'})接近 0
核函数值k(x,x′)接近1.当两个数据点x和x′距离很远时,核函数值核函数值k(x,x′)接近0
这样我们把核函数的值作为第三个维度的数据拓展了一个数据点的信息,通过更高维度我们可以更好地解决问题
运动基元 (Movement Primitives, MP)
运动基元是一些基础的运动模式,我们可以通过这些基础动作的组合和调整来实现复杂的运动任务.比如对应一个三自由度的机械臂,我们可以把该机械臂的抓取动作分解成三个伺服电机的各自的旋转动作,这样每一个伺服电机的动作就可以被称为一个运动基元
简单讲完一些基本的概念,我们先看结论,KMP算法是干什么用的?举个例子,如果我们有一个带有噪声的正弦图像,使用KMP算法我们可以构建出一个平滑的轨迹拟合这个图像
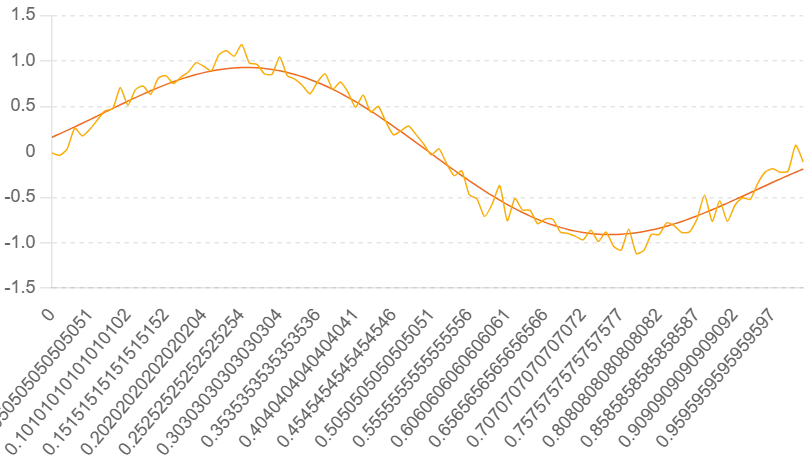
python代码:
<code>import numpy as np
from sklearn.kernel_ridge import KernelRidge
import matplotlib.pyplot as plt
# 生成示范轨迹数据
def generate_demo_data():
t = np.linspace(0, 1, 100) # 时间
y = np.sin(2 * np.pi * t) + 0.1 * np.random.randn(100) # 带噪声的正弦轨迹
return t, y
# 核函数轨迹基元
def kmp_trajectory(t, y, t_new, gamma=10, alpha=1):
# 使用核岭回归
model = KernelRidge(kernel='rbf', gamma=gamma, alpha=alpha)code>
model.fit(t[:, np.newaxis], y)
y_new = model.predict(t_new[:, np.newaxis])
return y_new
# 主程序
if __name__ == "__main__":
# 生成示范轨迹数据
t, y = generate_demo_data()
# 生成新的时间点
t_new = np.linspace(0, 1, 100)
# 使用KMP生成新的轨迹
y_new = kmp_trajectory(t, y, t_new)
# 绘制结果
plt.figure()
plt.plot(t, y, 'b.', label='示范轨迹')code>
plt.plot(t_new, y_new, 'r-', label='生成轨迹')code>
plt.xlabel('时间')
plt.ylabel('轨迹')
plt.legend()
plt.title('KMP轨迹生成')
plt.show()
这个代码是直接调用库中的岭回归算法,并不知道其具体的运算流程,接下来我们详细剖析一下:
首先导入库
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import cho_solve, cho_factor
from scipy.optimize import minimize
然后生成示范数据,这里我们假定只有一维,并带有噪声的正弦和余弦数据
def generate_noisy_demo_data():
t = np.linspace(0, 10, 100)
x = np.sin(t) + 0.1 * np.random.randn(t.shape[0])
y = np.cos(t) + 0.1 * np.random.randn(t.shape[0])
return t.reshape(-1, 1), np.vstack((x, y)).T
生成的示范数据 x 和 y 带有噪声
x
(
t
)
=
sin
(
t
)
+
ϵ
x
x(t)=\sin(t)+\epsilon_x
x(t)=sin(t)+ϵx
y
(
t
)
=
cos
(
t
)
+
ϵ
y
y(t)=\cos(t)+\epsilon_y
y(t)=cos(t)+ϵy
其中
ϵ
x
\epsilon_x
ϵx和
ϵ
y
\epsilon_y
ϵy是服从正态分布
N
(
0
,
0.
1
2
)
N(0,0.1^2)
N(0,0.12)的噪声
然后我们定义核函数,这里我们使用径向基函数核 (RBF Kernel) / 高斯核 (Gaussian Kernel)
def rbf_kernel(x1, x2, length_scale=1.0, variance=1.0):
sqdist = np.sum(x1**2, 1).reshape(-1, 1) + np.sum(x2**2, 1) - 2 * np.dot(x1, x2.T)
return variance * np.exp(-0.5 / length_scale**2 * sqdist)
定义了 Radial Basis Function (RBF) 核函数
k
(
x
1
,
x
2
)
=
v
a
r
i
a
n
c
e
⋅
exp
(
−
1
2
⋅
l
e
n
g
t
h
_
s
c
a
l
e
2
∣
∣
x
1
−
x
2
∣
∣
2
)
k(x_1,x_2)=variance\cdot \exp(-\frac{1}{2\cdot length\_scale^2}||x_1-x_2||^2)
k(x1,x2)=variance⋅exp(−2⋅length_scale21∣∣x1−x2∣∣2)
用于计算训练数据点之间的相似性
定义函数计算均值和协方差
def compute_mean_and_covariance(data):
mean = np.mean(data, axis=0)
covariance = np.cov(data.T)
return mean, covariance
定义函数计算KL散度
def kl_divergence(mu_p, cov_p, mu_q, cov_q):
dim = mu_p.shape[0]
cov_q_inv = np.linalg.inv(cov_q)
term1 = np.log(np.linalg.det(cov_q) / np.linalg.det(cov_p))
term2 = np.trace(cov_q_inv @ cov_p)
term3 = (mu_q - mu_p).T @ cov_q_inv @ (mu_q - mu_p)
kl_div = 0.5 * (term1 - dim + term2 + term3)
return kl_div
KL散度的定义
KL散度的作用
KL散度是度量两个概率分布之间差异的度量,常用于概率模型的优化、变分推断和信息论中。在KMP的高级实现中,KL散度可能用于以下情况:
分布匹配:确保生成的运动分布与目标分布(例如示范数据的分布)尽可能接近。优化目标:在优化过程中使用KL散度作为目标函数的一部分,使得模型参数的调整能够最小化分布之间的差异。
在更复杂的KMP实现中,KL散度可能用于优化控制策略,使生成的轨迹不仅与示范数据的均值和协方差匹配,还能在概率分布层面上保持一致
KL散度的推导过程:
KL散度的定义:
D
K
L
(
P
∣
∣
Q
)
=
∫
p
(
x
)
log
p
(
x
)
q
(
x
)
d
x
D_{KL}(P||Q)=\int p(x)\log\frac{p(x)}{q(x)}dx
DKL(P∣∣Q)=∫p(x)logq(x)p(x)dx
将高斯分布的概率密度函数代入上面的
K
L
散度公式
D
K
L
(
P
∣
∣
Q
)
=
∫
p
(
x
)
log
p
(
x
)
q
(
x
)
d
x
=
∫
p
(
x
)
log
1
(
2
π
)
d
/
2
∣
K
∣
1
/
2
exp
(
−
1
2
(
x
−
μ
)
T
K
−
1
(
x
−
μ
)
)
1
(
2
π
)
d
/
2
∣
K
^
∣
1
/
2
exp
(
−
1
2
(
x
−
μ
^
)
T
K
^
−
1
(
x
−
μ
^
)
)
d
x
化简对数为
:
log
p
(
x
)
q
(
x
)
=
log
1
(
2
π
)
d
/
2
∣
K
∣
1
/
2
−
log
1
(
2
π
)
d
/
2
∣
K
^
∣
1
/
2
−
1
2
(
x
−
μ
)
T
K
−
1
(
x
−
μ
)
+
1
2
(
x
−
μ
^
)
T
K
^
−
1
(
x
−
μ
^
)
=
1
2
[
log
∣
K
^
∣
∣
K
∣
−
(
x
−
μ
)
T
K
−
1
(
x
−
μ
)
+
(
x
−
μ
^
)
T
K
^
−
1
(
x
−
μ
^
)
]
将对数整合回
K
L
散度公式
:
D
K
L
(
P
∣
∣
Q
)
=
∫
1
2
p
(
x
)
log
∣
K
^
∣
∣
K
∣
d
x
−
∫
1
2
p
(
x
)
(
x
−
μ
)
T
K
−
1
(
x
−
μ
)
d
x
+
∫
1
2
p
(
x
)
(
x
−
μ
^
)
T
K
^
−
1
(
x
−
μ
^
)
d
x
对这三部分积分
:
∫
p
(
x
)
log
∣
K
^
∣
∣
K
∣
d
x
=
1
2
log
∣
K
^
∣
∣
K
∣
∫
p
(
x
)
(
x
−
μ
)
T
K
−
1
(
x
−
μ
)
d
x
=
t
r
(
K
−
1
K
)
=
d
∫
p
(
x
)
(
x
−
μ
^
)
T
K
^
−
1
(
x
−
μ
^
)
d
x
=
t
r
(
K
^
−
1
K
)
+
(
μ
−
μ
^
)
T
K
^
−
1
(
μ
−
μ
^
)
其中重点步骤
:
因为
(
x
−
μ
)
T
K
−
1
(
x
−
μ
)
是一个标量
,
所以
t
r
(
(
x
−
μ
)
T
K
−
1
(
x
−
μ
)
)
=
(
x
−
μ
)
T
K
−
1
(
x
−
μ
)
,
所以
E
(
(
x
−
μ
)
T
K
−
1
(
x
−
μ
)
)
=
E
(
t
r
(
(
x
−
μ
)
T
K
−
1
(
x
−
μ
)
)
)
=
E
(
t
r
(
K
−
1
(
x
−
μ
)
T
(
x
−
μ
)
)
)
=
t
r
(
K
−
1
E
(
(
x
−
μ
)
T
(
x
−
μ
)
)
)
=
t
r
(
K
−
1
K
)
=
d
由此可以顺利推出第二和第三个积分
最终得到
K
L
散度在高斯分布下的积分出来结果
:
D
K
L
(
P
∣
∣
Q
)
=
1
2
(
log
∣
K
^
∣
∣
K
∣
−
d
+
t
r
(
K
^
−
1
K
)
+
(
μ
−
μ
^
)
T
K
^
−
1
(
μ
−
μ
^
)
)
将高斯分布的概率密度函数代入上面的KL散度公式\\ D_{KL}(P||Q)=\int p(x)\log\frac{p(x)}{q(x)}dx\\ =\int p(x)\log\frac{\frac{1}{(2\pi)^{d/2}|K|^{1/2}}\exp(-\frac{1}{2}(x-\mu)^TK^{-1}(x-\mu))}{\frac{1}{(2\pi)^{d/2}|\hat K|^{1/2}}\exp(-\frac{1}{2}(x-\hat \mu)^T\hat K^{-1}(x-\hat \mu))}dx\\ 化简对数为:\\ \log\frac{p(x)}{q(x)}= \log\frac{1}{(2\pi)^{d/2}|K|^{1/2}}-\log\frac{1}{(2\pi)^{d/2}|\hat K|^{1/2}} -\frac{1}{2}(x-\mu)^TK^{-1}(x-\mu) +\frac{1}{2}(x-\hat \mu)^T\hat K^{-1}(x-\hat \mu)\\ =\frac{1}{2}[\log\frac{|\hat K|}{|K|} -(x-\mu)^TK^{-1}(x-\mu) +(x-\hat \mu)^T\hat K^{-1}(x-\hat \mu)]\\ 将对数整合回KL散度公式:\\ D_{KL}(P||Q)=\int \frac{1}{2}p(x)\log\frac{|\hat K|}{|K|}dx -\int \frac{1}{2}p(x)(x-\mu)^TK^{-1}(x-\mu)dx +\int \frac{1}{2}p(x)(x-\hat \mu)^T\hat K^{-1}(x-\hat \mu)dx\\ 对这三部分积分:\\ \int p(x)\log\frac{|\hat K|}{|K|}dx=\frac{1}{2}\log\frac{|\hat K|}{|K|}\\ \int p(x)(x-\mu)^TK^{-1}(x-\mu)dx=tr(K^{-1}K)=d\\ \int p(x)(x-\hat \mu)^T\hat K^{-1}(x-\hat \mu)dx=tr(\hat K^{-1}K)+(\mu-\hat \mu)^T\hat K^{-1}(\mu-\hat \mu)\\ 其中重点步骤:\\ 因为(x-\mu)^TK^{-1}(x-\mu)是一个标量,所以tr((x-\mu)^TK^{-1}(x-\mu))=(x-\mu)^TK^{-1}(x-\mu),\\所以E((x-\mu)^TK^{-1}(x-\mu))=E(tr((x-\mu)^TK^{-1}(x-\mu)))\\ =E(tr(K^{-1}(x-\mu)^T(x-\mu)))=tr(K^{-1}E((x-\mu)^T(x-\mu)))\\ =tr(K^{-1}K)=d\\ 由此可以顺利推出第二和第三个积分\\ 最终得到KL散度在高斯分布下的积分出来结果:\\ D_{KL}(P||Q)=\frac{1}{2}(\log\frac{|\hat K|}{|K|}-d +tr(\hat K^{-1}K)+(\mu-\hat \mu)^T\hat K^{-1}(\mu-\hat \mu))\\
将高斯分布的概率密度函数代入上面的KL散度公式DKL(P∣∣Q)=∫p(x)logq(x)p(x)dx=∫p(x)log(2π)d/2∣K^∣1/21exp(−21(x−μ^)TK^−1(x−μ^))(2π)d/2∣K∣1/21exp(−21(x−μ)TK−1(x−μ))dx化简对数为:logq(x)p(x)=log(2π)d/2∣K∣1/21−log(2π)d/2∣K^∣1/21−21(x−μ)TK−1(x−μ)+21(x−μ^)TK^−1(x−μ^)=21[log∣K∣∣K^∣−(x−μ)TK−1(x−μ)+(x−μ^)TK^−1(x−μ^)]将对数整合回KL散度公式:DKL(P∣∣Q)=∫21p(x)log∣K∣∣K^∣dx−∫21p(x)(x−μ)TK−1(x−μ)dx+∫21p(x)(x−μ^)TK^−1(x−μ^)dx对这三部分积分:∫p(x)log∣K∣∣K^∣dx=21log∣K∣∣K^∣∫p(x)(x−μ)TK−1(x−μ)dx=tr(K−1K)=d∫p(x)(x−μ^)TK^−1(x−μ^)dx=tr(K^−1K)+(μ−μ^)TK^−1(μ−μ^)其中重点步骤:因为(x−μ)TK−1(x−μ)是一个标量,所以tr((x−μ)TK−1(x−μ))=(x−μ)TK−1(x−μ),所以E((x−μ)TK−1(x−μ))=E(tr((x−μ)TK−1(x−μ)))=E(tr(K−1(x−μ)T(x−μ)))=tr(K−1E((x−μ)T(x−μ)))=tr(K−1K)=d由此可以顺利推出第二和第三个积分最终得到KL散度在高斯分布下的积分出来结果:DKL(P∣∣Q)=21(log∣K∣∣K^∣−d+tr(K^−1K)+(μ−μ^)TK^−1(μ−μ^))
开始编写KMP计算流程
<code>class KMP:
def __init__(self, length_scale=1.0, variance=1.0, noise=1e-5):
self.length_scale = length_scale
self.variance = variance
self.noise = noise
self.X_train = None
self.Y_train = None
self.K_inv = None
def fit(self, X_train, Y_train):
self.X_train = X_train
self.Y_train = Y_train
self.optimize_hyperparameters(X_train, Y_train)
def optimize_hyperparameters(self, X_train, Y_train):
def objective(params):
self.length_scale, self.variance = params
K = rbf_kernel(X_train, X_train, self.length_scale, self.variance) + self.noise * np.eye(len(X_train))
self.K_inv = cho_solve(cho_factor(K), np.eye(len(K)))
mu_s, cov_s, pred_mean, pred_cov = self.predict_with_mean_and_cov(X_train)
demo_mean, demo_cov = compute_mean_and_covariance(Y_train)
kl_div = kl_divergence(demo_mean, demo_cov, pred_mean, pred_cov)
return kl_div
initial_params = [self.length_scale, self.variance]
result = minimize(objective, initial_params, bounds=((1e-5, 1e5), (1e-5, 1e5)))
self.length_scale, self.variance = result.x
def predict(self, X_test):
K_s = rbf_kernel(X_test, self.X_train, self.length_scale, self.variance)
K_ss = rbf_kernel(X_test, X_test, self.length_scale, self.variance) + self.noise * np.eye(len(X_test))
mu_s = K_s.dot(self.K_inv).dot(self.Y_train)
cov_s = K_ss - K_s.dot(self.K_inv).dot(K_s.T)
return mu_s, cov_s
def predict_with_mean_and_cov(self, X_test):
mu_s, cov_s = self.predict(X_test)
mean, covariance = compute_mean_and_covariance(mu_s)
return mu_s, cov_s, mean, covariance
我们使用核方法来拟合示范数据并预测新的轨迹,这里定义了fit函数计算训练数据的核矩阵
K
K
K,计算
K
K
K的 Cholesky 分解并求逆,定义predict函数计算测试数据与训练数据之间的核矩阵
K
s
K_s
Ks,计算测试数据的核矩阵
K
s
s
K_{ss}
Kss,计算预测的均值和协方差,最优化KL散度值,使得模型参数的调整能够最小化分布之间的差异
K
i
j
=
k
(
x
i
,
x
j
)
+
n
o
i
s
e
⋅
δ
i
j
K_{ij}=k(x_i,x_j)+noise\cdot \delta_{ij}
Kij=k(xi,xj)+noise⋅δij
K
−
1
=
(
C
h
o
l
e
s
k
y
(
K
)
)
−
1
⋅
(
C
h
o
l
e
s
k
y
(
K
)
)
−
T
K^{-1}=(Cholesky(K)) ^{−1} \cdot(Cholesky(K)) ^{−T}
K−1=(Cholesky(K))−1⋅(Cholesky(K))−T
K
s
i
j
=
k
(
x
t
e
s
t
i
,
x
t
r
a
i
n
j
)
K_{s_{ij}}=k(x_{test_i} ,x_{train_j})
Ksij=k(xtesti,xtrainj)
K
s
s
i
j
=
k
(
x
t
e
s
t
i
,
x
t
e
s
t
j
)
+
n
o
i
s
e
⋅
δ
i
j
K_{ss_{ij}}=k(x_{test_i} ,x_{test_j})+noise\cdot \delta_{ij}
Kssij=k(xtesti,xtestj)+noise⋅δij
μ
s
=
K
s
⋅
K
−
1
⋅
Y
t
r
a
i
n
\mu_s=K_s\cdot K^{-1}\cdot Y_{train}
μs=Ks⋅K−1⋅Ytrain
Σ
s
=
K
s
s
−
K
s
⋅
K
−
1
⋅
K
s
T
\Sigma_s=K_{ss}-K_s\cdot K^{-1}\cdot K_s^T
Σs=Kss−Ks⋅K−1⋅KsT
然后初始化进行绘制
t, demo_data = generate_noisy_demo_data()
kmp = KMP(length_scale=1.0, variance=1.0)
kmp.fit(t, demo_data)
mu_s, cov_s, pred_mean, pred_cov = kmp.predict_with_mean_and_cov(t)
def plot_kmp_noisy(t, demo_data, mu_s):
plt.figure(figsize=(10, 5))
plt.plot(t, demo_data[:, 0], 'r', label='Noisy Demo X')code>
plt.plot(t, demo_data[:, 1], 'b', label='Noisy Demo Y')code>
plt.plot(t, mu_s[:, 0], 'r--', label='Predicted X')code>
plt.plot(t, mu_s[:, 1], 'b--', label='Predicted Y')code>
plt.legend()
plt.xlabel('Time')
plt.ylabel('Trajectory')
plt.title('KMP')
plt.show()
plot_kmp_noisy(t, demo_data, mu_s)
结果如下图
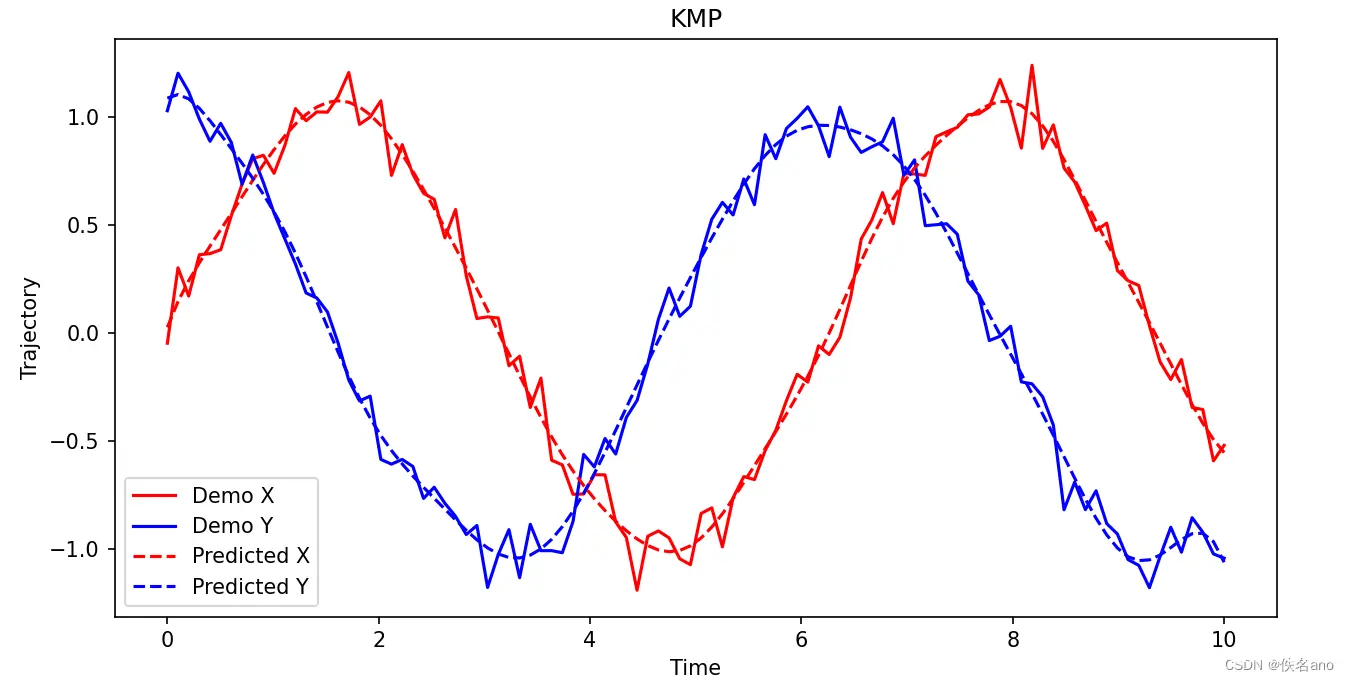
以上就是KMP算法的大致流程了
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。