【机器学习】Grid Search: 一种系统性的超参数优化方法
CSDN 2024-08-12 09:31:03 阅读 65


🌈个人主页: 鑫宝Code
🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础
💫个人格言: "如无必要,勿增实体"

文章目录
Grid Search: 一种系统性的超参数优化方法引言什么是Grid Search?Grid Search的工作流程1. 定义超参数范围2. 创建超参数网格3. 训练和评估模型4. 选择最佳超参数
随机森林下的 Grid Search步骤1: 导入必要的库步骤2: 准备数据步骤3: 定义超参数的网格步骤4: 创建GridSearchCV对象步骤5: 执行Grid Search步骤6: 分析结果
Grid Search的优缺点优点缺点
总结
Grid Search: 一种系统性的超参数优化方法
引言
在机器学习领域,模型的性能往往取决于一系列可调参数的选择,这些参数被称为“超参数”。与模型权重不同,超参数不能从数据中直接学习得到,而是需要人为设定。超参数的选择对模型最终的表现有着至关重要的影响,因此寻找最佳超参数组合是机器学习项目中的一个关键步骤。本文将详细介绍Grid Search(网格搜索)这一超参数优化技术。
什么是Grid Search?
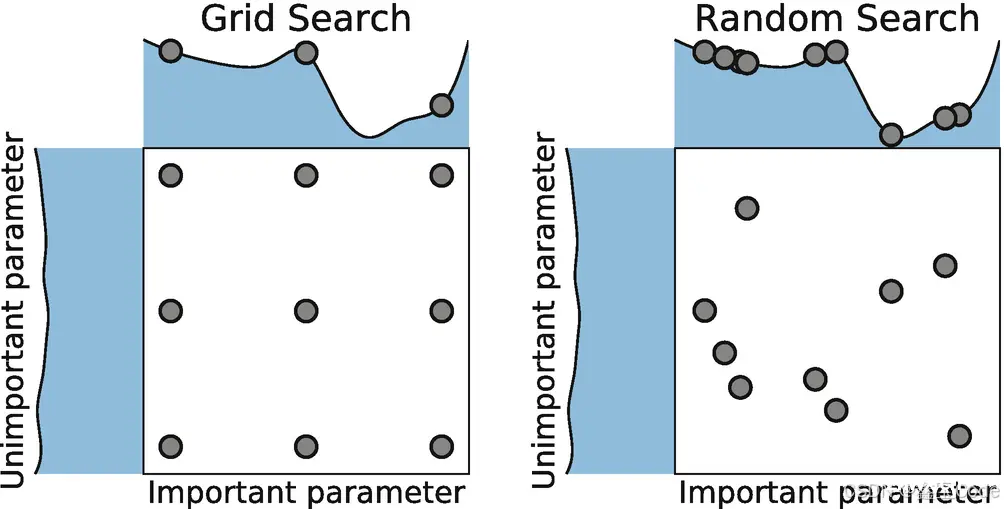
Grid Search是一种用于自动搜索给定超参数空间中最佳模型参数组合的方法。它通过创建一个包含所有待评估超参数值的网格,然后遍历这个网格中的每一个点来完成搜索过程。对于每个网格点,即超参数的一个特定组合,Grid Search会训练模型并评估其性能,最后选择性能最优的那个组合作为最佳超参数设置。
Grid Search的工作流程
1. 定义超参数范围
首先,需要为每个超参数定义一个候选值的列表或区间。例如,如果我们要调整决策树的深度和最小样本分割数,我们可以定义如下:
决策树深度:[3, 5, 7, 9]最小样本分割数:[2, 5, 10]
2. 创建超参数网格

基于上述定义,可以创建一个超参数网格,其中包含所有可能的超参数组合。在这个例子中,我们有:
| 决策树深度 | 最小样本分割数 |
|---|---|
| 3 | 2 |
| 3 | 5 |
| 3 | 10 |
| 5 | 2 |
| 5 | 5 |
| 5 | 10 |
| 7 | 2 |
| 7 | 5 |
| 7 | 10 |
| 9 | 2 |
| 9 | 5 |
| 9 | 10 |
3. 训练和评估模型
对于网格中的每一个超参数组合,Grid Search将重复以下步骤:
使用该组合训练模型。在验证集上评估模型性能。记录结果。
4. 选择最佳超参数
最后,根据在验证集上的表现,选择性能最好的超参数组合。通常,性能的度量标准可以是准确率、F1分数、AUC-ROC等,具体取决于问题类型和业务需求。
随机森林下的 Grid Search
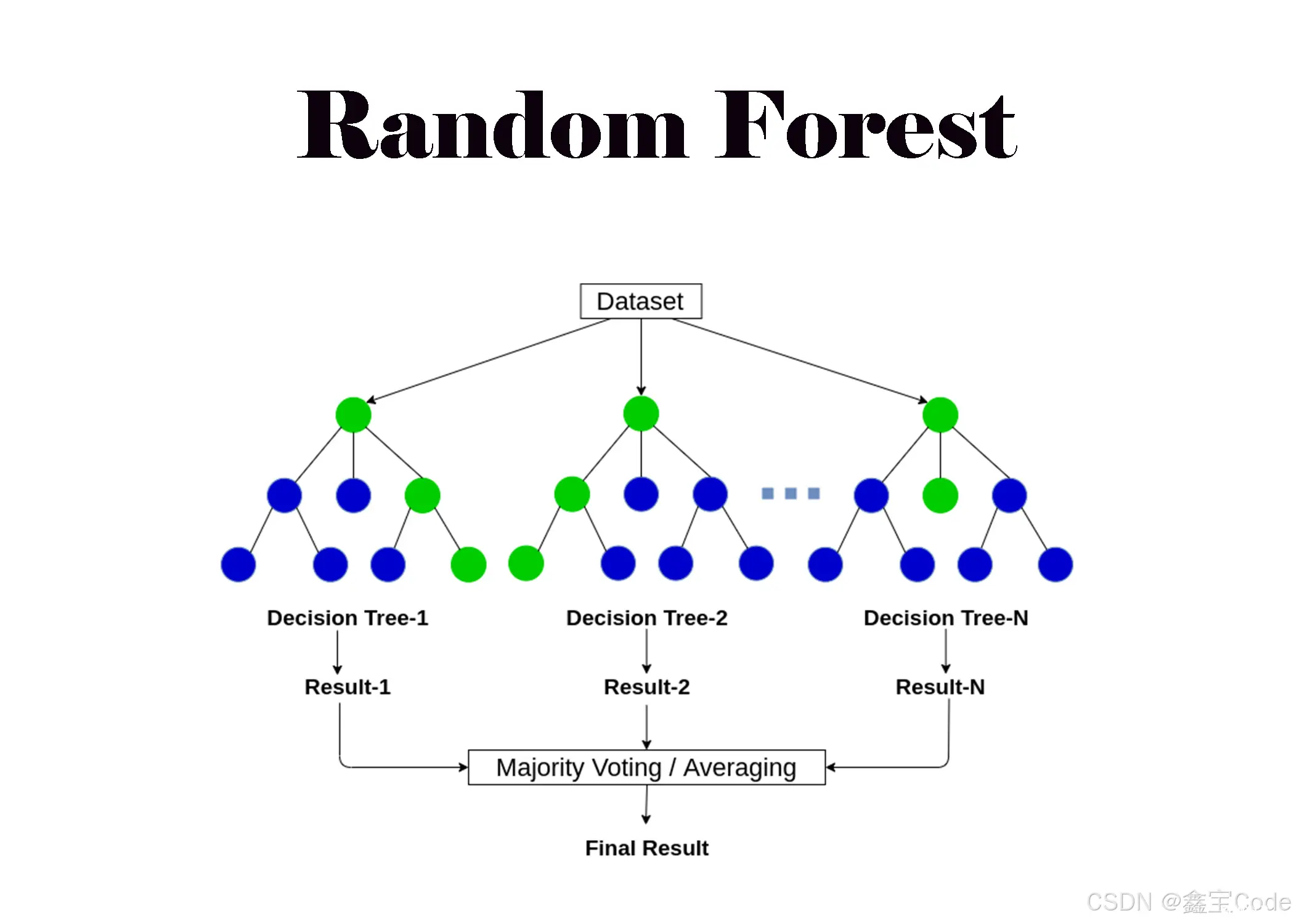
随机森林(Random Forest)是一种常用的集成学习方法,它通过构建多个决策树并将它们的预测结果综合起来,以提高预测精度和防止过拟合。在随机森林中,有几个关键的超参数需要调整,比如树的数量(<code>n_estimators)、特征的最大数量(max_features)、节点分裂所需的最小样本数(min_samples_split)等。下面我们将使用Python的Scikit-Learn库来展示如何使用Grid Search对随机森林的超参数进行优化。以下代码仅供参考🐶
步骤1: 导入必要的库
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
步骤2: 准备数据
这里我们使用Iris数据集作为示例。
data = load_iris()
X = data.data
y = data.target
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
步骤3: 定义超参数的网格
param_grid = {
'n_estimators': [10, 50, 100, 200],
'max_features': ['auto', 'sqrt', 'log2'],
'min_samples_split': [2, 5, 10],
'min_samples_leaf': [1, 2, 4],
}
步骤4: 创建GridSearchCV对象
rf = RandomForestClassifier(random_state=42)
grid_search = GridSearchCV(estimator=rf, param_grid=param_grid, cv=5, scoring='accuracy', verbose=2, n_jobs=-1)code>
这里的cv=5表示我们使用5折交叉验证,scoring='accuracy'code>指定了评估指标为准确率,verbose=2让输出更详细,n_jobs=-1则意味着使用所有可用的处理器核心来加速搜索过程。
步骤5: 执行Grid Search
grid_search.fit(X_train, y_train)
步骤6: 分析结果
best_params = grid_search.best_params_
best_score = grid_search.best_score_
print("Best Parameters: ", best_params)
print("Best Score (Cross-Validated): ", best_score)
# 使用最佳超参数重新训练模型,并在测试集上评估
best_rf = grid_search.best_estimator_
y_pred = best_rf.predict(X_test)
test_accuracy = accuracy_score(y_test, y_pred)
print("Test Accuracy: ", test_accuracy)
这段代码将会输出最佳超参数组合以及对应的交叉验证得分和测试集准确率。
Grid Search的优缺点
优点
简单易用:Grid Search的实现相对直接,不需要复杂的算法知识。保证找到最优解:只要超参数空间被充分覆盖,Grid Search一定能找到最优解。
缺点
计算成本高:随着超参数数量和每个参数的候选值数量增加,Grid Search的计算复杂度呈指数级增长。不考虑参数间交互:Grid Search假设超参数之间是相互独立的,这在实际中往往是不成立的。
总结
Grid Search是一种有效的超参数优化方法,尤其适用于超参数空间较小的情况。然而,在处理具有大量超参数的复杂模型时,其计算效率低下成为主要瓶颈。在实际应用中,应根据具体情况权衡是否采用Grid Search,或考虑更高效的替代方案,如Randomized Search或Bayesian Optimization。
以上内容仅为Grid Search概念的简要介绍,深入实践时还需要结合具体案例和工具,如Scikit-Learn库中的GridSearchCV类,进行更细致的学习和应用。


下一篇: AI生成PPT怎么弄?本文的四种方法让你高效搞定PPT制作过程
本文标签
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。