【AI学习笔记】初学机器学习西瓜书概要记录(一)机器学习基础知识篇
秃头队长 2024-10-01 17:01:07 阅读 84
初学机器学习西瓜书的概要记录(一)机器学习基础知识篇(已完结)
初学机器学习西瓜书的概要记录(二)常用的机器学习方法篇(持续更新)
初学机器学习西瓜书的概要记录(三)进阶知识篇(待更)
文字公式撰写不易,随意学习,转载请注明!谢谢
(一)机器学习基础知识篇
1.1 机器学习1.2 典型的机器学习过程1.2 机器学习理论1.3 基本术语1.4 归纳偏好1.5 NFL定理2.1 泛化能力2.2 过拟合和欠拟合2.3 三大问题2.4 评估方法2.5 调参与验证集2.6 性能度量2.7 比较检验3.1 线性回归3.2 最小二乘解3.3 多元线性回归3.4 广义线性模型3.5 广义线性模型3.6 对率回归求解3.7 线性判别分析(LDA)3.7 线性判别分析(LDA)的多类推广3.9 多分类学习基本思路3.10 类别不平衡
以下内容出自周志华老师亲讲西瓜书
1.1 机器学习
(1)经典定义:利用经验改善系统自身的性能。(经验->数据)
随着该领域的发展,目前主要研究智能数据分析的理论和方法,并已成为智能数据分析技术的源泉之一
1.2 典型的机器学习过程
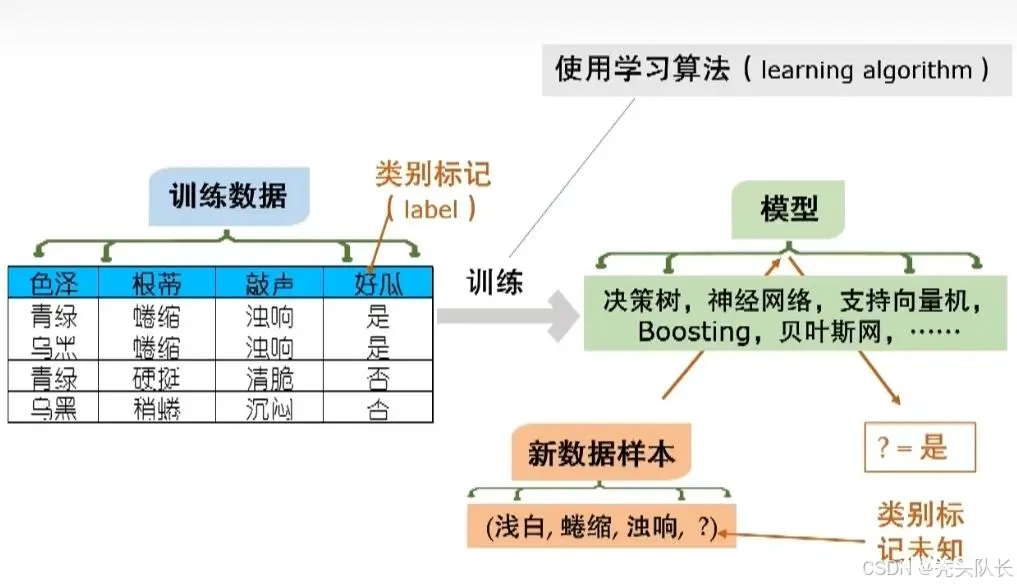
适用于全局 - 模型 适用于局部 - 模式(pattern)
1.2 机器学习理论
PAC(Probably Approximately Correct 概率近似正确模型)
P
(
∣
f
(
x
)
−
y
∣
≤
ϵ
)
≥
1
−
δ
P(|f(x) - y|\leq \epsilon )\geq 1- \delta
P(∣f(x)−y∣≤ϵ)≥1−δ
建立一个模型,对于数据
x
x
x 样本得到一个模型
f
f
f,那么模型
f
f
f 会对
x
x
x进行一个判断,即
f
(
x
)
f(x)
f(x),我们希望这个模型判断特别准,即逼近真实结果
y
y
y。那么可以表达为
∣
f
(
x
)
−
y
∣
≤
ϵ
|f(x) - y|\leq \epsilon
∣f(x)−y∣≤ϵ,即它们俩的差别小于一个很小的数。希望能得到这样一个模型
f
f
f,但并不是每次都能得到,所以希望能以很高的概率去得到它,很高的概率意味着
P
(
∣
f
(
x
)
−
y
∣
≤
ϵ
)
≥
1
−
δ
P(|f(x) - y|\leq \epsilon )\geq 1- \delta
P(∣f(x)−y∣≤ϵ)≥1−δ,如果
δ
\delta
δ非常小,那么获取到这个模型的概率就非常高。
为什么不追求该模型一定是准的,即
∣
f
(
x
)
−
y
∣
=
0
|f(x) - y| = 0
∣f(x)−y∣=0,且一定能获取到该模型?
机器学习通常解决的问题具有高度的不确定性、高度的复杂性,甚至不知道怎么去做它。当我们的知识已经不能精确的给我结果的时候,我从数据里去分析,希望能从数据中得到答案。
P
?
=
N
P
P?=NP
P?=NP
P问题:在多项式时间内,能找到该问题的解。
NP问题:在多项式时间内,给一个解,能判断它是不是解。
如果
∣
f
(
x
)
−
y
∣
=
0
|f(x) - y| = 0
∣f(x)−y∣=0,
P
=
1
P=1
P=1,那么意味着每次都能给到最佳答案,那么即证明了
P
=
N
P
P=NP
P=NP
1.3 基本术语
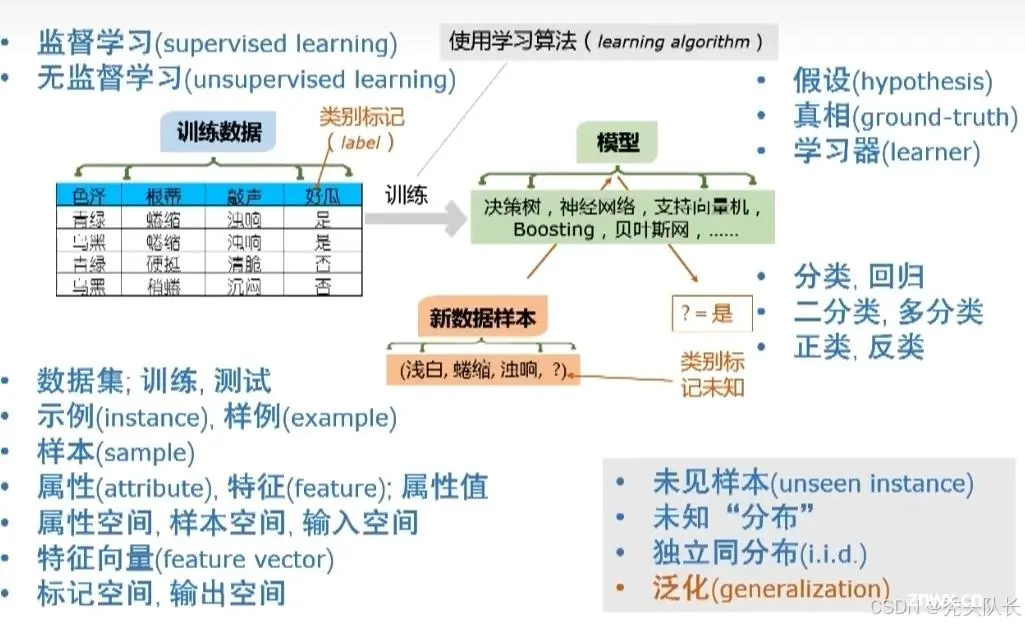
非监督学习:拿到的数据中,没有希望结果,聚类、密度估计
监督学习:预测内容、分类回归
1.4 归纳偏好
机器学习算法学习过程中对某种类型假设的偏好
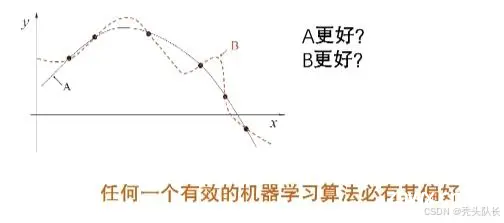
一般原则:奥卡姆剃刀(若非必要,勿增实体)
学习算法的归纳偏好是否与问题本身匹配,大多数时候直接决定了算法能否取得好的性能!
1.5 NFL定理
NFL定理:一个算法
a
a
a若在某些问题比领一个算法
b
b
b好,必存在另一些问题
b
b
b比
a
a
a好。
NFL定理的重要前提:所有“问题”出现的机会相同、或所有问题同等重要
实际情形并非如此,我们通常只关注自己正在试图解决的问题
脱离具体问题,空泛地谈论“什么学习算法更好”毫无意义!
最优方案往往来自:按需设计、度身定制
2.1 泛化能力
泛化能力强,能很好地适用于 unseen instance
2.2 过拟合和欠拟合
泛化误差:在“未来”样本上的误差
经验误差:在训练集上的误差,亦称“训练误差”
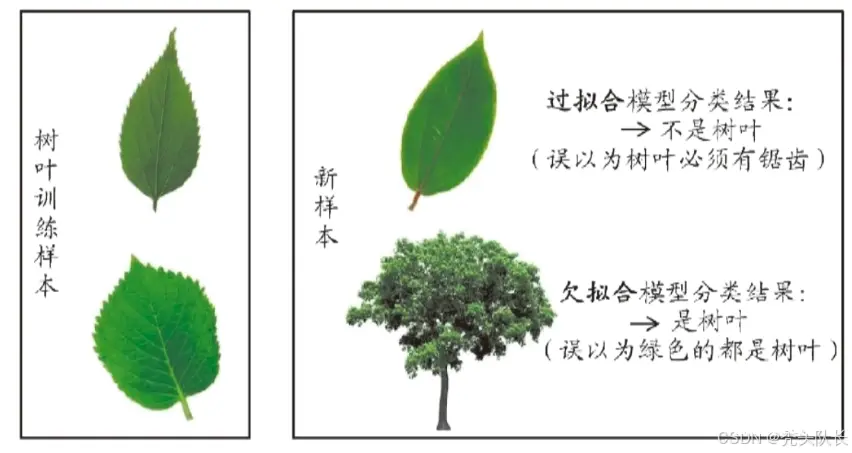
过拟合(over fitting),所有的算法都是在缓解过拟合,在学习具体算法时需要关注该算法靠什么去缓解过拟合,以及缓解过拟合的策略在什么情况下会失效,明白以上两点便把握了该算法应该在什么时候用。
2.3 三大问题
三个关键问题:
(1)如何获得测试结果 评估方法
(2)如何评估性能优劣 性能度量
(3)如何判断实质差别 比较检验
2.4 评估方法
关键:怎么获得“测试集”?
测试集应该与训练集"互斥"
常见方法:
(1)留出法(hold-out)

例如训练一个100条数据的数据集,训练出的模型称为
M
100
M_{100}
M100,它的性能判断
E
r
r
100
Err_{100}
Err100,但是
E
r
r
100
Err_{100}
Err100是无法得到的,因此我们划分出80条数据集进行训练,得到模型
M
80
M_{80}
M80,则用剩下的20条数据进行测试得到
E
r
r
80
Err_{80}
Err80,使用
E
r
r
80
Err_{80}
Err80去近似
E
r
r
100
Err_{100}
Err100。但是如果测试集使用的数据过多,那么
M
80
M_{80}
M80已经不是
M
100
M_{100}
M100模型了,随着训练集的减少,该近似效果就会变差,同时又希望测试集更多,才会使
E
r
r
80
Err_{80}
Err80的测试结果更准确。因此大部分情况下都是使用经验值20%去做测试。在通过抽取的训练集训练出模型后,通过性能判断
E
r
r
80
Err_{80}
Err80选择最终的模型,此时并不是把
M
80
M_{80}
M80作为最终的模型,而是使用所有数据集训练得到
M
100
M_{100}
M100.
(2)交叉验证法(cross vaildation)
因为在留出法中,每次都是挑取一定比例的数据作为训练集,所以存在有的数据永远都没存在在训练集中。
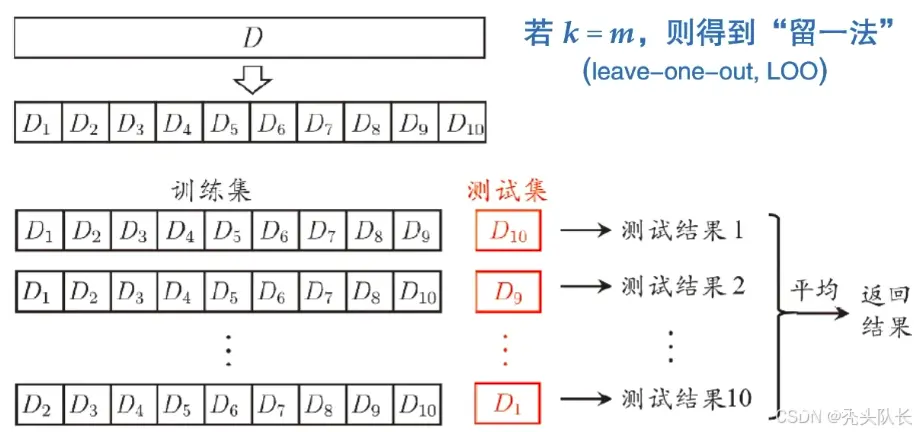
(3)自助法(bootstrap)
基于“自助采样”(bootstrap sampling)亦称“有放回采样”、“可重复采样”
在十个彩色小球的筐内,随机抽取一个小球,复制一份放到训练集中。最后未抽取到的颜色小球作为测试集。
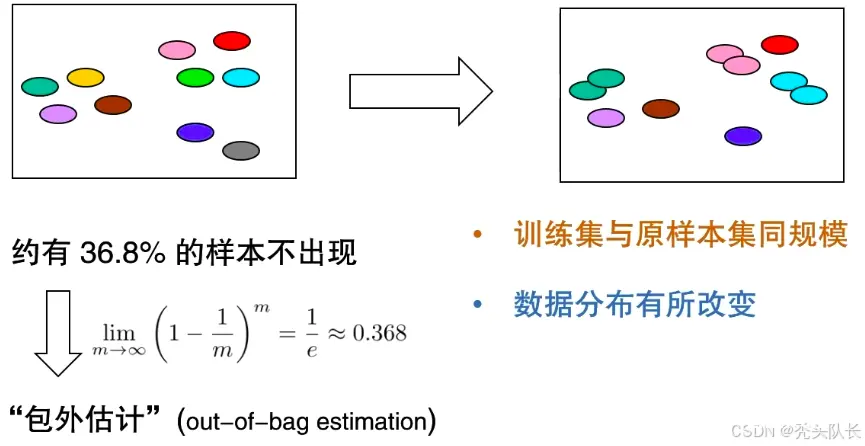
2.5 调参与验证集
算法的参数:一般由人工设定,亦称"超参数"
调参的过程相似:先产生若干模型,然后基于某种评估方法进行选择。
在拟合一条直线时,对于一个模型
y
=
a
x
d
+
b
x
+
c
y=ax^d+bx+c
y=axd+bx+c,其中次数
d
d
d可以由用户提供,即超参数,剩下的则有学习确定
参数调的好不好往往对最终性能有关键影响
在训练集中单独留出用于调参数的数据称为验证集
算法参数选定后,要用“训练集+验证集”重新训练最终模型
2.6 性能度量
性能度量时衡量模型泛化能力的评价标准,反映了任务需求
使用不同的性能度量往往会导致不同的评判结果
什么样的模型是好的,不仅取决于算法和数据,还取决于任务需求
(1)回归任务常用均方误差:
E
(
f
;
D
)
=
1
m
∑
i
=
1
m
(
f
(
x
i
)
−
y
i
)
2
E(f;D) = {1\over m}\sum^m_{i=1}(f(x_i)-y_i)^2
E(f;D)=m1i=1∑m(f(xi)−yi)2
(2)分类任务错误率:
E
(
f
;
D
)
=
1
m
∑
i
=
1
m
∏
(
f
(
x
i
)
≠
y
i
)
E(f;D) = {1\over m}\sum^m_{i=1}\prod(f(x_i) \neq y_i)
E(f;D)=m1i=1∑m∏(f(xi)=yi)
(3)查准率和查全率
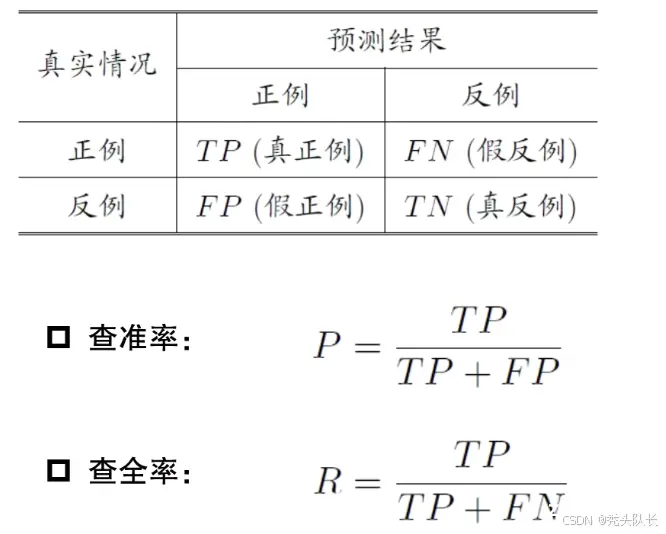

2.7 比较检验
在某种度量下取得评估结果后,不可以直接比较以评判优劣
因为:
(1)测试性能不等于泛化性能
(2)测试性能随着测试集的变化而变化
(3)很多机器学习算法本身有一定随机性
统计假设检验为学习器性能比较提供了总要依据
两学习器比较:
交叉验证t检验(基于成对t检验)McNemar检验(基于列联表,卡方检验)
3.1 线性回归
线性模型试图学得一个通过属性的线性组合来进行预测的函数
f
(
x
)
=
w
1
x
1
+
w
2
x
2
+
.
.
.
+
w
d
x
d
+
b
f(x) = w_1x_1+w_2x_2+...+w_dx_d+b
f(x)=w1x1+w2x2+...+wdxd+b
向量形式:
f
(
x
)
=
w
T
x
+
b
f(x) = w^Tx+b
f(x)=wTx+b
f
(
x
i
)
=
w
T
x
i
+
b
使得
f
(
x
i
)
≈
y
i
f(x_i)=w^Tx_i+b 使得 f(x_i)\approx y_i
f(xi)=wTxi+b使得f(xi)≈yi
对于线性回归模型,其擅长处理数值属性,对于离散属性转换成连续数值。在转化的过程中需要考虑是否有序的关系,例如对于高、中、低,但是对于一个西瓜的颜色,他们的序是无法判断的,这时候就不能简单的划分为1、0.5、0。对于这样的离散属性,可以将其表示为三维向量。
离散属性的处理:若有序,则连续化,否则转化为
k
k
k维向量
令均方误差最小化,有:
(
w
∗
,
b
∗
)
=
a
r
g
m
i
n
(
w
,
b
)
∑
i
=
1
m
(
f
(
x
i
)
−
y
i
)
2
(w^*,b^*) = \underset{(w,b) }{argmin}\sum^m_{i=1}(f(x_i)-y_i)^2
(w∗,b∗)=(w,b)argmini=1∑m(f(xi)−yi)2
=
a
r
g
m
i
n
(
w
,
b
)
∑
i
=
1
m
(
y
i
−
w
x
i
−
b
)
2
= \underset{(w,b) }{argmin}\sum^m_{i=1}(y_i - wx_i-b)^2
=(w,b)argmini=1∑m(yi−wxi−b)2
对
E
(
w
,
b
)
=
∑
i
=
1
m
(
y
i
−
w
x
i
−
b
)
2
E(w,b)=\sum^m_{i=1}(y_i - wx_i-b)^2
E(w,b)=∑i=1m(yi−wxi−b)2进行最小二乘估计
3.2 最小二乘解
E
(
w
,
b
)
=
∑
i
=
1
m
(
y
i
−
w
x
i
−
b
)
2
E(w,b)=\sum^m_{i=1}(y_i - wx_i-b)^2
E(w,b)=∑i=1m(yi−wxi−b)2 分别对
w
w
w 和
b
b
b 求偏导
∂
E
(
w
,
b
)
∂
w
=
2
∑
i
=
1
m
(
y
i
−
w
x
i
−
b
)
x
i
=
2
(
w
∑
i
=
1
m
x
i
2
−
∑
i
=
1
m
(
y
i
−
b
)
x
i
)
{\partial E(w,b) \over \partial w} =2\sum^m_{i=1}(y_i - wx_i-b)x_i \\ =2\left(w \sum^m_{i=1} x^2_i - \sum^m_{i=1} (y_i-b)x_i \right)
∂w∂E(w,b)=2i=1∑m(yi−wxi−b)xi=2(wi=1∑mxi2−i=1∑m(yi−b)xi)
∂
E
(
w
,
b
)
∂
b
=
−
2
∑
i
=
1
m
(
y
i
−
w
x
i
−
b
)
=
2
(
m
b
−
∑
i
=
1
m
(
y
i
−
w
x
i
)
)
{\partial E(w,b) \over \partial b} =-2\sum^m_{i=1}(y_i - wx_i-b) \\=2\left(mb - \sum^m_{i=1} (y_i-wx_i) \right)
∂b∂E(w,b)=−2i=1∑m(yi−wxi−b)=2(mb−i=1∑m(yi−wxi))
令导数等为 0,得到闭式解:
w
=
∑
i
=
1
m
y
i
(
x
i
−
x
ˉ
)
∑
i
=
1
m
x
i
2
−
1
m
(
∑
i
=
1
m
x
i
)
2
w={\sum^m_{i=1} y_i(x_i-\bar x) \over \sum^m_{i=1} x^2_i - {1\over m} \left(\sum^m_{i=1} x_i \right)^2}
w=∑i=1mxi2−m1(∑i=1mxi)2∑i=1myi(xi−xˉ)
b
=
1
m
∑
i
=
1
m
(
y
i
−
w
x
i
)
b=\ {1\over m} \sum^m_{i=1} (y_i-wx_i)
b= m1i=1∑m(yi−wxi)
偏导的真实含义是变化率,对于该凸函数,极值点就是最值点。
3.3 多元线性回归
f
(
x
i
)
=
w
T
x
i
+
b
使得
f
(
x
i
)
≈
y
i
f(x_i)=w^Tx_i+b 使得 f(x_i)\approx y_i
f(xi)=wTxi+b使得f(xi)≈yi
x
i
=
(
x
i
1
;
x
i
2
;
.
.
.
;
x
i
d
)
y
i
∈
R
x_i=(x_{i1};x_{i2};...;x_{id}) \\y_i\in \Bbb{R}
xi=(xi1;xi2;...;xid)yi∈R
把
w
w
w 和
b
b
b 吸收入向量形式
w
^
=
(
w
;
b
)
\hat{w} = (w;b)
w^=(w;b)数据集表示为
X
=
(
x
11
x
12
⋯
x
1
d
1
x
21
x
22
⋯
x
2
d
1
⋮
⋮
⋮
⋱
⋮
x
m
1
x
m
2
⋯
x
m
d
1
)
=
(
x
1
T
1
x
2
T
1
⋮
⋮
x
m
T
1
)
X = \begin{pmatrix} x_{11} & x_{12} & \cdots & x_{1d} & 1 \\ x_{21} & x_{22} & \cdots & x_{2d} & 1 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_{m1} & x_{m2} & \cdots & x_{md} & 1 \\ \end{pmatrix} = \begin{pmatrix} x_{1}^T & 1 \\ x_{2}^T & 1 \\ \vdots & \vdots \\ x_{m}^T & 1 \\ \end{pmatrix}
X=
x11x21⋮xm1x12x22⋮xm2⋯⋯⋮⋯x1dx2d⋱xmd11⋮1
=
x1Tx2T⋮xmT11⋮1
y
=
(
y
1
;
y
2
;
.
.
.
;
y
m
)
y=(y_1;y_2;...;y_m)
y=(y1;y2;...;ym)
同样采用最小二乘法求解,有
w
^
∗
=
a
r
g
m
i
n
w
^
(
y
−
X
w
^
)
T
(
y
−
X
w
^
)
\hat{w}^* = \underset{\hat{w}}{argmin}(y-X\hat{w})^T(y-X\hat{w})
w^∗=w^argmin(y−Xw^)T(y−Xw^)
令
E
w
^
=
(
y
−
X
w
^
)
T
(
y
−
X
w
^
)
E_{\hat{w}}=(y-X\hat{w})^T(y-X\hat{w})
Ew^=(y−Xw^)T(y−Xw^),对
w
^
\hat{w}
w^求导:
∂
E
(
w
^
)
∂
w
^
=
2
X
T
(
X
w
^
−
y
)
{\partial E(\hat{w}) \over \partial \hat{w}} =2X^T(X\hat{w}-y)
∂w^∂E(w^)=2XT(Xw^−y) 令其为零可得
w
^
\hat{w}
w^
若
X
T
X
X^TX
XTX 满秩或正定,则
w
^
∗
=
(
X
T
X
)
−
1
X
T
y
\hat {w}^*=(X^TX)^{-1}X^Ty
w^∗=(XTX)−1XTy
若
X
T
X
X^TX
XTX 不满秩,则可解出多个
w
^
\hat{w}
w^
此时需求助于归纳偏好,或引入正则化。
3.4 广义线性模型
线性模型的变化
对于样例
(
x
,
y
)
,
y
∈
R
(x,y),y\in \Bbb{R}
(x,y),y∈R,希望线性模型的预测值逼近真实标记,则得到线性回归模型
y
=
w
T
x
+
b
y=w^Tx+b
y=wTx+b
令预测值逼近
y
y
y的衍生物,若令
l
n
y
=
w
T
x
+
b
lny=w^Tx+b
lny=wTx+b则得到对数线性回归,实际是在用
e
w
T
x
+
b
e^{w^Tx+b}
ewTx+b逼近
y
y
y
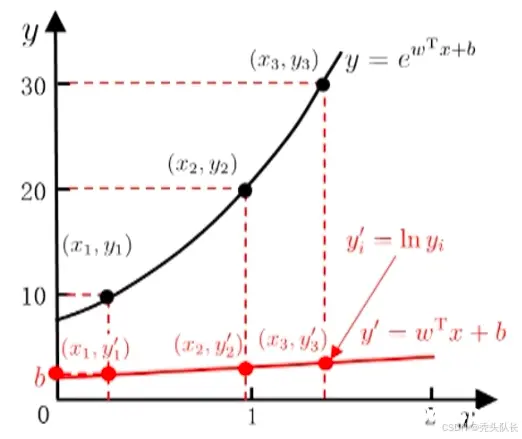
一般形式:
y
=
g
−
1
(
w
T
x
+
b
)
y=g^{-1}(w^Tx+b)
y=g−1(wTx+b)其中
g
−
1
g^{-1}
g−1为单调可微的联系函数
3.5 广义线性模型
二分类任务
线性回归模型产生的实值输出
z
=
w
T
x
+
b
z=w^Tx+b
z=wTx+b
期望输出
y
∈
{
0
,
1
}
y \in \{0,1\}
y∈{ 0,1}
找出
z
z
z和
y
y
y的联系函数,理想的“单位阶跃函数”
y
=
{
1
,
z<0
0.5
,
z=0
1
,
z>0
y = \begin{cases} 1, & \text{z<0} \\[2ex] 0.5, & \text{z=0} \\[2ex] 1, & \text{z>0} \end{cases}
y=⎩
⎨
⎧1,0.5,1,z<0z=0z>0
性质不好,不连续,需要找替代函数。常用单调可微、任意阶可导的对数几率函数(logistic function),简称对率函数
y
=
1
1
+
e
−
z
y={1\over 1+e^{-z}}
y=1+e−z1

注意:Logistic与“逻辑”没有半毛钱关系!
1.Logistic 源自 Logit,不是Logic
2.实数值,并非“非0即1”的逻辑值
以对率函数为联系函数:
y
=
1
1
+
e
−
z
变为
y
=
1
1
+
e
−
(
w
T
x
+
b
)
y={1\over 1+e^{-z}} 变为y={1\over 1+e^{-(w^Tx+b)}}
y=1+e−z1变为y=1+e−(wTx+b)1即
l
n
y
1
−
y
=
w
T
x
+
b
ln{y \over 1-y}=w^Tx+b
ln1−yy=wTx+b
y
1
−
y
y \over 1-y
1−yy :几率(odds),反映了
x
x
x作为正例的相对可能性
对数几率回归,简称对率回归
无需事先假设数据分布可得到“类别”的近似概率预测可直接应用现有数值优化算法求取最优解
注意:它是分类学习算法
3.6 对率回归求解
若将
y
y
y看做类后验概率估计
p
(
y
=
1
∣
x
)
p(y=1|x)
p(y=1∣x),则
l
n
y
1
−
y
=
w
T
x
+
b
ln{y \over 1-y}=w^Tx+b
ln1−yy=wTx+b可写为
l
n
p
(
y
=
1
∣
x
)
p
(
y
=
0
∣
x
)
=
w
T
x
+
b
ln{p(y=1|x) \over p(y=0|x)}=w^Tx+b
lnp(y=0∣x)p(y=1∣x)=wTx+b于是,可使用极大似然法
给定数据集
{
(
x
i
,
y
i
)
}
i
=
1
m
\{ (x_i,y_i) \}^m_{i=1}
{(xi,yi)}i=1m,最大化对数似然函数
l
(
w
,
b
)
=
∑
i
=
1
m
l
n
p
(
y
i
∣
x
i
;
w
,
b
)
l(w,b)=\sum^m_{i=1}lnp(y_i|x_i;w,b)
l(w,b)=i=1∑mlnp(yi∣xi;w,b)
令
β
=
(
w
;
b
)
,
x
^
=
(
x
;
1
)
\beta=(w;b),\hat{x}=(x;1)
β=(w;b),x^=(x;1),则
w
T
x
+
b
w^Tx+b
wTx+b 可简写为
β
T
x
^
\beta^T\hat{x}
βTx^
再令:
p
1
(
x
i
^
;
β
)
=
p
(
y
=
1
∣
x
^
;
β
)
=
e
w
T
x
+
b
1
+
e
w
T
x
+
b
p
0
(
x
i
^
;
β
)
=
p
(
y
=
0
∣
x
^
;
β
)
=
1
−
p
1
(
x
i
^
;
β
)
=
1
1
+
e
w
T
x
+
b
p_1(\hat{x_i};\beta) =p(y=1|\hat{x};\beta)={e^{w^Tx+b}\over 1+e^{w^Tx+b}} \\ p_0(\hat{x_i};\beta) =p(y=0|\hat{x};\beta)=1-p_1(\hat{x_i};\beta) ={1\over 1+e^{w^Tx+b}}
p1(xi^;β)=p(y=1∣x^;β)=1+ewTx+bewTx+bp0(xi^;β)=p(y=0∣x^;β)=1−p1(xi^;β)=1+ewTx+b1
则似然项可重写为
p
(
y
i
∣
x
i
;
w
i
,
b
)
=
y
i
p
1
(
x
^
i
;
β
)
+
(
1
−
y
i
)
p
0
(
x
^
i
;
β
)
p(y_i|x_i;w_i,b)=y_ip_1(\hat{x}_i;\beta)+(1-y_i)p_0(\hat{x}_i;\beta)
p(yi∣xi;wi,b)=yip1(x^i;β)+(1−yi)p0(x^i;β)
于是最大化似然函数
l
(
w
,
b
)
=
∑
i
=
1
m
l
n
p
(
y
i
∣
x
i
;
w
,
b
)
l(w,b)=\sum^m_{i=1}lnp(y_i|x_i;w,b)
l(w,b)=∑i=1mlnp(yi∣xi;w,b) 等价为最小化:
l
(
β
)
=
∑
i
=
1
m
(
−
y
i
β
T
x
^
i
+
l
n
(
1
+
e
β
T
x
^
i
)
)
l(\beta)=\sum^m_{i=1}\left( -y_i\beta^T\hat{x}_i+ln(1+e^{\beta^T\hat{x}_i}) \right)
l(β)=i=1∑m(−yiβTx^i+ln(1+eβTx^i))
高阶连续可导凸函数,可用经典的数值优化方法,如梯度下降法/牛顿法
MAX(P(真是+)P(预测为+) + P(真是-)P(预测为-)),在极大似然法中通常需要加对数,因为其概率可能是很小值,当概率连乘时可能会出现浮点数下溢,在取对数后乘法变成加法。
即
l
n
(
y
∗
e
β
T
x
1
+
e
β
T
x
+
(
1
−
y
)
1
1
+
e
β
T
x
)
=
l
n
y
e
β
T
x
+
1
−
y
1
+
e
β
T
x
=
l
n
(
y
e
β
T
x
+
1
−
y
)
−
l
n
(
1
+
e
β
T
x
)
ln(y*{e^{\beta^T x} \over 1+e^{\beta^T x}}+(1-y){1\over 1+e^{\beta^T x}}) \\ =ln{ye^{\beta^T x} + 1-y \over 1+e^{\beta^T x}}\\ =ln(ye^{\beta^T x} + 1-y)-ln(1+e^{\beta^T x})
ln(y∗1+eβTxeβTx+(1−y)1+eβTx1)=ln1+eβTxyeβTx+1−y=ln(yeβTx+1−y)−ln(1+eβTx)
当
y
=
1
y=1
y=1时为
β
T
x
−
l
n
(
1
+
e
β
T
x
)
\beta^Tx-ln(1+e^{\beta^T x})
βTx−ln(1+eβTx)
当
y
=
0
y=0
y=0时为
−
l
n
(
1
+
e
β
T
x
)
-ln(1+e^{\beta^T x})
−ln(1+eβTx)
因此可写为通项:
M
A
X
(
y
β
T
x
−
l
n
(
1
+
e
β
T
x
)
)
=
M
I
N
(
−
y
β
T
x
+
l
n
(
1
+
e
β
T
x
)
)
=
M
I
N
(
l
n
(
1
+
e
β
T
x
)
e
y
β
T
x
)
MAX (y\beta^Tx-ln(1+e^{\beta^T x})) \\ =MIN (-y\beta^Tx+ln(1+e^{\beta^T x})) \\ =MIN (ln{(1+e^{\beta^T x}) \over e^{y\beta^Tx}})
MAX(yβTx−ln(1+eβTx))=MIN(−yβTx+ln(1+eβTx))=MIN(lneyβTx(1+eβTx))
其中
β
T
x
^
=
w
T
x
+
b
\beta^T\hat{x} = w^Tx+b
βTx^=wTx+b
M
I
N
(
l
n
(
1
+
e
f
(
x
)
)
e
y
f
(
x
)
)
MIN (ln{(1+e^{f(x)}) \over e^{yf(x)}})
MIN(lneyf(x)(1+ef(x)))
一般情况下,即使是凸函数,也很难通过直接求导为零得到最优解(需要求逆),通常通过梯度下降的方式求解
最终解一定是梯度为零的点,梯度为零的点不一定是最优解梯度下降通常是迭代解法
(
w
i
+
1
=
w
i
+
δ
w
)
(w_{i+1}=w_{i}+\delta w)
(wi+1=wi+δw),迭代解法比较容易并行化,更适合计算机处理,往往更快
3.7 线性判别分析(LDA)
用线性模型做分类,有两种基本思路,以上讲的是先用线性模型做回归,然后找一个联系函数,把我们要做的分类结果和回归结果联系起来,那么能否直接去做分类。
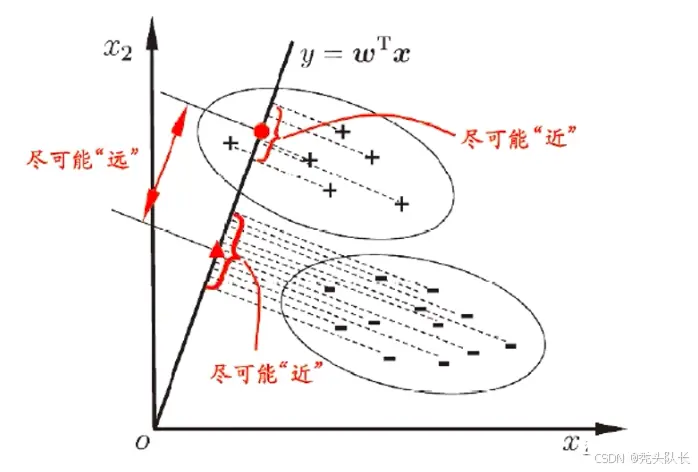
由于将样例投影到一条直线(低维空间),因此也被视为一种“监督降维”技术。
给定数据集
{
(
x
i
,
y
i
)
}
i
=
1
m
\{(x_i,y_i) \}^m_{i=1}
{(xi,yi)}i=1m
第
i
i
i类示例的集合
X
i
X_i
Xi
第
i
i
i类示例的均值向量
μ
i
\mu_i
μi
第
i
i
i类示例的协方差矩阵
∑
i
\sum_i
∑i
两类样本的中心在直线上的投影:
w
T
μ
0
w^T \mu_0
wTμ0 和
w
T
μ
1
w^T \mu_1
wTμ1
两类样本的协方差:
w
T
∑
0
w
w^T\sum_0 w
wT∑0w 和
w
T
∑
1
w
w^T\sum_1w
wT∑1w
同类样例的投影点尽可能接近:
w
T
∑
0
w
w^T\sum_0 w
wT∑0w 和
w
T
∑
1
w
w^T\sum_1w
wT∑1w 尽可能小
异类样例的投影点尽可能远离:
∣
∣
w
T
μ
0
−
w
T
μ
1
∣
∣
2
2
||w^T\mu_0 -w^T\mu_1||^2_2
∣∣wTμ0−wTμ1∣∣22 尽可能大
于是,最大化
J
=
∣
∣
w
T
μ
0
−
w
T
μ
1
∣
∣
2
2
w
T
∑
0
w
+
w
T
∑
1
w
=
w
T
(
μ
0
−
μ
1
)
(
μ
0
−
μ
1
)
T
w
w
T
(
∑
0
+
∑
1
)
w
J={||w^T\mu_0 -w^T\mu_1||^2_2 \over w^T\sum_0 w +w^T\sum_1w}={w^T(\mu_0-\mu_1)(\mu_0-\mu_1)^Tw \over w^T(\sum_0+\sum_1)w}
J=wT∑0w+wT∑1w∣∣wTμ0−wTμ1∣∣22=wT(∑0+∑1)wwT(μ0−μ1)(μ0−μ1)Tw
类内散度矩阵
S
w
=
∑
0
+
∑
1
=
∑
x
∈
X
0
(
x
−
μ
0
)
(
x
−
μ
0
)
T
+
∑
x
∈
X
1
(
x
−
μ
1
)
(
x
−
μ
1
)
T
S_w=\sum_0+\sum_1\\ =\sum_{x\in X_0}(x-\mu_0)(x-\mu_0)^T+\sum_{x\in X_1}(x-\mu_1)(x-\mu_1)^T
Sw=0∑+1∑=x∈X0∑(x−μ0)(x−μ0)T+x∈X1∑(x−μ1)(x−μ1)T类间散度矩阵
S
b
=
(
μ
0
−
μ
1
)
(
μ
0
−
μ
1
)
T
S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^T
Sb=(μ0−μ1)(μ0−μ1)T
LDA目标:最大化广义瑞利商
J
=
w
T
S
b
w
w
T
S
w
w
J={w^TS_bw\over w^TS_ww}
J=wTSwwwTSbw
可以看出
w
w
w 大小无关紧要,其方向才是关键。
求解:令
w
T
S
w
w
=
1
w^TS_ww=1
wTSww=1最大化广义瑞利商等价形式为:
m
i
n
w
−
w
T
S
b
w
s
.
t
.
w
T
S
w
w
=
1
\underset{w}{min}-w^TS_bw \\ s.t. \quad w^TS_ww=1
wmin−wTSbws.t.wTSww=1
运用拉格朗日乘子法:即
w
T
S
w
w
−
1
=
0
w^TS_ww-1=0
wTSww−1=0
−
w
T
S
b
w
+
λ
(
w
T
S
w
w
−
1
)
-w^TS_bw+\lambda( w^TS_ww-1)
−wTSbw+λ(wTSww−1)
令其对
w
w
w偏导为零,即
−
(
S
b
+
S
b
T
)
w
+
λ
(
S
w
+
S
w
T
)
w
-(S_b+S_b^T)w+ \lambda(S_w+S_w^T)w
−(Sb+SbT)w+λ(Sw+SwT)w
其中类内散度矩阵和类间散度矩阵均为对称阵,则:
−
2
S
b
w
+
2
λ
S
w
w
=
0
S
b
w
=
λ
S
w
w
-2S_bw+2\lambda S_ww=0 \\ S_bw=\lambda S_ww
−2Sbw+2λSww=0Sbw=λSww
由
S
b
S_b
Sb定义,有
S
b
w
=
(
μ
0
−
μ
1
)
(
μ
0
−
μ
1
)
T
w
S_bw=(\mu_0-\mu_1)(\mu_0-\mu_1)^Tw
Sbw=(μ0−μ1)(μ0−μ1)Tw,注意到
(
μ
0
−
μ
1
)
T
w
(\mu_0-\mu_1)^Tw
(μ0−μ1)Tw 为标量,且
w
w
w 大小无关紧要,令其等于
λ
\lambda
λ,于是:
w
=
S
w
−
1
(
μ
0
−
μ
1
)
w=S_w^{-1}(\mu_0-\mu_1)
w=Sw−1(μ0−μ1)
实践中通常是进行奇异值分解
S
w
=
U
∑
V
T
S_w=U\sum V^T
Sw=U∑VT,然后
S
w
−
1
=
V
∑
−
1
U
T
S^{-1}_w=V\sum^{-1} U^T
Sw−1=V∑−1UT
3.7 线性判别分析(LDA)的多类推广
假设有
N
N
N个类
全局散度矩阵
S
t
=
S
b
+
S
w
=
∑
i
=
1
m
(
x
I
−
μ
)
(
x
i
−
μ
)
T
S_t=S_b+S_w=\sum^m_{i=1}(x_I-\mu)(x_i-\mu)^T
St=Sb+Sw=i=1∑m(xI−μ)(xi−μ)T类内散度矩阵
S
w
=
∑
i
=
1
N
S
w
i
S
w
i
=
∑
x
∈
X
i
(
x
−
μ
i
)
(
x
−
μ
i
)
T
S_w=\sum^N_{i=1}S_{w_i} \\ S_{w_i} = \sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^T
Sw=i=1∑NSwiSwi=x∈Xi∑(x−μi)(x−μi)T类内散度矩阵
S
b
=
S
t
−
S
w
=
∑
i
=
1
N
m
i
(
μ
i
−
μ
)
(
μ
i
−
μ
)
T
S_b=S_t-S_w=\sum_{i=1}^Nm_i(\mu_i-\mu)(\mu_i-\mu)^T
Sb=St−Sw=i=1∑Nmi(μi−μ)(μi−μ)T
多类LDA有多种实现方法:采用
S
b
,
S
w
,
S
t
S_b,S_w,S_t
Sb,Sw,St中的任何两个,例如
m
a
x
W
t
r
(
W
T
S
b
W
)
t
r
(
W
T
S
w
W
)
W
∈
R
d
×
(
N
−
1
)
⇒
S
b
W
=
λ
S
w
W
\underset{W}{max}{tr(W^TS_bW)\over tr(W^TS_wW)} \quad W \in \Bbb{R}^{d\times(N-1)} \\ \Rightarrow S_bW=\lambda S_wW
Wmaxtr(WTSwW)tr(WTSbW)W∈Rd×(N−1)⇒SbW=λSwW
W
W
W 的闭式解是
S
w
−
1
S
b
S_w^{-1}S_b
Sw−1Sb的
d
′
(
≤
N
−
1
)
d'(\leq N-1)
d′(≤N−1)个最大非零广义特征值对应的特征向量组成的矩阵
3.9 多分类学习基本思路
除了LDA技术,比如知识向量机,如何基于两类模型去做多类分类。
拆解法:将一个多分类任务拆分为若干个二分类任务求解
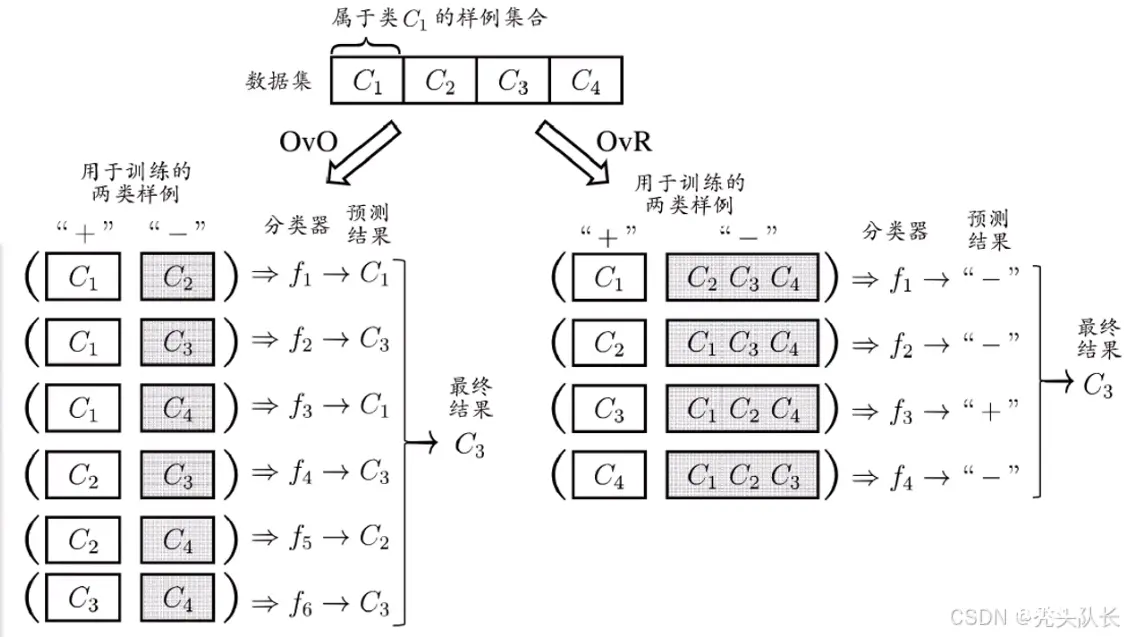
最终的分类结果选择预测结果次数最多的那类,若次数相同可以根据置信度选择。
OvO(one)每次只考虑将一个类作为正类,而另一个作为负类。
(1)训练
N
(
N
−
1
)
2
N(N-1) \over 2
2N(N−1)个分类器,存储开销和测试时间大
(2)训练只用两个类的样例,训练时间短OvR(rest) 每次只考虑将一个类作为正类,其余作为负类。
(1)训练
N
N
N个分类器,存储开销和测试时间小
(2)训练用到全部样例,训练时间长
预测性能取决于具体数据分布,多数情况下两者差不多。
3.10 类别不平衡
不同类别的样本比例相差很大,小类往往更重要
基本思路:
若
y
1
−
y
>
1
{y \over 1-y }>1
1−yy>1则预测为正例
⇒
\Rightarrow
⇒ 若
y
1
−
y
>
m
+
m
−
{y \over 1-y }>{m^+ \over m^- }
1−yy>m−m+则预测为正例
基本策略:再缩放
y
′
1
−
y
′
=
y
1
−
y
×
m
−
m
+
{y' \over 1-y' } ={y \over 1-y }\times {m^- \over m^+ }
1−y′y′=1−yy×m+m−
然而,精确估计
m
−
m
+
{m^- \over m^+ }
m+m−通常很困难!
常见类别不平衡学习方法
过采样 例如:SMOTE欠采样 例如:EasyEnsemble阈值移动
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。