文章目录

按章节排序第 1 章 绪论第 2 章 模型评估与选择第 3 章 线性模型第 4 章 决策树第 5 章 神经网络第 6 章 支持向量机第 7 章 贝叶斯分类器第 8 章 集成学习第 9 章 聚类第10章 降维与度量学习第11章 特征选择与稀疏学习第12章 计算学习理论第13章 半监督学习第14章 概率图模型第15章 规则学习第16章 强化学习附 录

按时间排序(第一版第45次印刷, 2024年1月):(第一版第40次印刷, 2022年11月):(第一版第36次印刷, 2021年5月):(第一版第35次印刷, 2020年11月):(第一版第34次印刷, 2020年7月):(第一版第33次印刷, 2020年4月):(第一版第31次印刷, 2019年9月):(第一版第27次印刷, 2018年6月):(第一版第26次印刷, 2018年5月):(第一版第25次印刷, 2018年3月):(第一版第24次印刷, 2018年1月):(第一版第23次印刷, 2017年10月):(第一版第22次印刷, 2017年9月):(第一版第21次印刷, 2017年8月)(第一版第20次印刷, 2017年7月):(第一版第19次印刷, 2017年6月):(第一版第18次印刷, 2017年5月):(第一版第17次印刷, 2017年4月):(第一版第16次印刷, 2017年3月):(第一版第15次印刷, 2017年2月):(第一版第14次印刷, 2016年12月):(第一版第13次印刷, 2016年11月):(第一版第10次印刷, 2016年9月)：(第一版第9次印刷, 2016年8月)(第一版第8次印刷, 2016年5月)：(第一版第7次印刷, 2016年4月)：(第一版第6次印刷, 2016年4月)：(第一版第5次印刷, 2016年3月)：(第一版第4次印刷, 2016年3月)：(第一版第3次印刷, 2016年3月)：(第一版第2次印刷, 2016年2月)：(第一版第1次印刷, 2016年1月)：

[本书因颇受欢迎，出版社提出重印，于是作者借机要求在每次重印时加入新的修订，省却让读者等待第二版的麻烦。为方便读者，所有修订内容都列举在此。其中部分修订是为了更便于读者理解，并非原文有误]

原勘误链接：https://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/MLbook2016.htm#errata

按章节排序

第 1 章 绪论

p.5, 第2段倒数第3行: “3、2、2” --> “3、3、3”p.5, 第2段倒数第2行: “

4

×

3

×

3

+

1

=

37

4 \times 3 \times 3 + 1 = 37

4×3×3+1=37” -->; “

4

×

4

×

4

+

1

=

65

4 \times 4 \times 4 + 1 = 65

4×4×4+1=65”p.6, 图1.2: 图中两处"清脆" --> “浊响”p.10, 倒数第7行: “Nilson” --> “Nilsson”p.15, 第5行: “居功” --> “厥功”

第 2 章 模型评估与选择

p.26, 边注第2行: “2.6 节” --> “2.5 节”

p.27, 式(2.1)：第一个"

↦

\mapsto

↦" --> “

→

\to

→”, 第二个"

↦

\mapsto

↦" --> “

=

=

=”

p.28, 第3段倒数第2行: “大量” --> “不少”

p.28, 边注: “例如 ……上百亿个参数” --> “机器学习常涉及两类参数: 一类是算法的参数, 亦称"超参数”, 数目常在10以内; 另一类是模型的参数, 数目可能很多, 例如……上百亿个参数. 两者调参方式相似, 均是产生多个模型之后基于某种评估方法来进行选择; 不同之处在于前者通常是由人工设定多个参数候选值后产生模型, 后者则是通过学习来产生多个候选模型(例如神经网络在不同轮数停止训练)."

p.31, 倒数第3行: “Event” --> “Even”

p.31, 图 2.3: 修订文件

p.34, 图 2.4(b): 修订文件

p.36, 倒数第5行: “(TPR, FPR)” --> “(FPR, TPR)”

p.38, 第6行: “

ϵ

m

′

\epsilon^{m'}

ϵm′” -->; “

(

m

m

′

)

ϵ

m

′

{m \choose m'} \epsilon^{m'}

(m′m​)ϵm′”

p.38, 式(2.27),

ϵ

0

×

m

\epsilon_0 \times m

ϵ0​×m -->

ϵ

×

m

\epsilon \times m

ϵ×m

p.38, 式(2.27),

ϵ

i

(

1

−

ϵ

)

m

−

i

\epsilon^{i} (1-\epsilon)^{m-i}

ϵi(1−ϵ)m−i -->

ϵ

0

i

(

1

−

ϵ

0

)

m

−

i

\epsilon_0^{i} (1-\epsilon_0)^{m-i}

ϵ0i​(1−ϵ0​)m−i

p.38, 式(2.27)：“

max

⁡

\max

max” --> “

min

⁡

\min

min”

p.39, 第1行，“大于” --> “小于”

p.39, 最后一行：“

[

−

∞

,

[-\infty,

[−∞,” --> “

(

−

∞

,

(-\infty,

(−∞,”，“

,

∞

]

, \infty]

,∞]” --> “

,

∞

)

, \infty)

,∞)”

p.39, 倒数第1行: “若平均错误率……临界值范围” --> “若_{$\tao_t$}位于临界值范围”

p.41, 式(2.32)的下一行: “自由度为~5” --> “自由度为~4”; “2.5706” --> “2.776”; “2.0150” --> “2.132”

p.41, 式(2.33)上面一行: “正态分布, 且均值 …… 因此变量” --> “正态分布. McNemar检验考虑变量”

p.41, 式(2.33)旁加边注: “

e

01

+

e

10

e_{01} + e_{10}

e01​+e10​ 通常很小, 需考虑连续性校正, 因此分子中有

−

1

-1

−1 项”

p.42, 表2.5下面一段的第三行: “服从正态分布，其均值” --> “的均值”

p.42, 倒数第二行加边注: “原始检验要求

k

k

k较大(例如

>

30

>30

>30)，若

k

k

k较小则倾向于认为无显著区别”

p.42, 表2.5后第四行：“

(

k

2

−

1

)

/

12

(k^2-1)/12

(k2−1)/12” --> "

(

k

2

−

1

)

/

12

N

(k^2-1)/12N

(k2−1)/12N"s

p.45, 第一个边注: “由式(2.37)” --> “考虑到噪声不依赖于

f

f

f, 由式(2.37)”

第 3 章 线性模型

p.55, 最后一行: 式子括号中的逗号改为分号

p.56, 图3.1中，红色第一和第二个点的坐标互换

p.58, 倒数第二行：“对率函数” --> “下面我们会看到, 对率回归求解的目标函数”

p.59, 式(3.27)加边注: “考虑

y

i

∈

{

0

,

1

}

y_i \in \{0, 1\}

yi​∈{ 0,1}”

p.59, 倒数第二行：“其第_$t+1$轮”–>“从当前_$\bm\beta$生成下一轮”

p.59, 式(3.29):

β

t

+

1

\bm\beta^{t+1}

βt+1 -->

β

′

\bm\beta^{'}

β′,

β

t

\bm\beta^{t}

βt -->

β

\bm\beta

β

p.60, 图3.3中：“

y

=

w

T

x

y = \bm{w}^{\rm T}\bm{x}

y=wTx,

y

y

y” --> “投影方向~

w

\bm{w}

w”

p.62, 第1行加边注: “

(

μ

0

−

μ

1

)

T

w

(\bm {\mu}_0 - \bm{\mu}_1)^{\rm T} \bm{w}

(μ0​−μ1​)Tw 是标量”

p.63, 式(3.45)下面一行: “

N

−

1

N-1

N−1个最大” --> “

d

′

d'

d′个最大非零”

p.63, 式(3.45)下面第2行: “矩阵.” --> “矩阵,

d

′

≤

N

−

1

d'\le N-1

d′≤N−1.”; 加边注: “最多有

N

−

1

N-1

N−1个非零特征值”

p.63, 式(3.45)下面第3行: “

N

−

1

N-1

N−1维” --> “

d

′

d'

d′维”

p.63, 式(3.45)下面第4行: “

N

−

1

N-1

N−1通常远小于数据原有的属性数” --> “

d

′

d'

d′通常远小于数据原有的属性数

d

d

d”

第 4 章 决策树

p.78, 图4.4, 从右往左数: 第二个叶结点改为“好瓜”，第三个叶结点改为“坏瓜”p.80, 倒数第2行：“算法4.2” --> “图 4.2 算法”p.85, 图4.8, 从右往左数: 第二个叶结点改为“好瓜”，第三个叶结点改为“坏瓜”p.85, 图4.8, 中间分支底层: “硬挺”–> “硬滑”p.89, 图4.9, 中间分支底层: “硬挺”–> “硬滑”

第 5 章 神经网络

p.100, 图5.5, 左图最上面的 “阈值

0.5

0.5

0.5” --> “阈值

1.5

1.5

1.5”

p.100, 图5.5, 左图最右边的 “阈值

0.5

0.5

0.5” --> “阈值

−

1.5

-1.5

−1.5”

p.100, 图5.5, 左图中间的"1 -1 -1 1" --> “1 1 -1 -1”

p.103, 最后一行的式子: 求和的"

q

q

q" --> “

l

l

l”

p.112, 图 5.14a: 修订文件

p.112, 式(5.24): 两处"

⊤

^{\top}

⊤" --> “

T

^{\rm T}

T”

p.114, 图5.15中, 卷积层 16@10x10 和 采样层 16@5x5 各去掉 8 个方块

p.119, 第14行: “318–362” -->; “533–536”

p.120, 第7行: “(1927 – )” --> “(1927 – 2016)”

第 6 章 支持向量机

p.123, 倒数第三行，“即可将

L

(

w

,

b

,

α

)

L(w,b,\alpha)

L(w,b,α)中的

w

w

w和

b

b

b消去，再考虑式(6.10)的约束，就得到式(6.6)的对偶问题：”–> “考虑式(6.10)的约束，即可将

L

(

w

,

b

,

α

)

L(w,b,\alpha)

L(w,b,α)中的

w

w

w和

b

b

b消去，得到式(6.6)的对偶问题：”

p.125, 第3行: “减小” --> “增大”

p.125, 第4行，第6行: “减幅” --> “增幅”

p.125, 第5行: “减小” --> “增长”

p.125, 式(6.18): “

y

s

y_s

ys​” --> “

1

/

y

s

1/y_s

1/ys​”

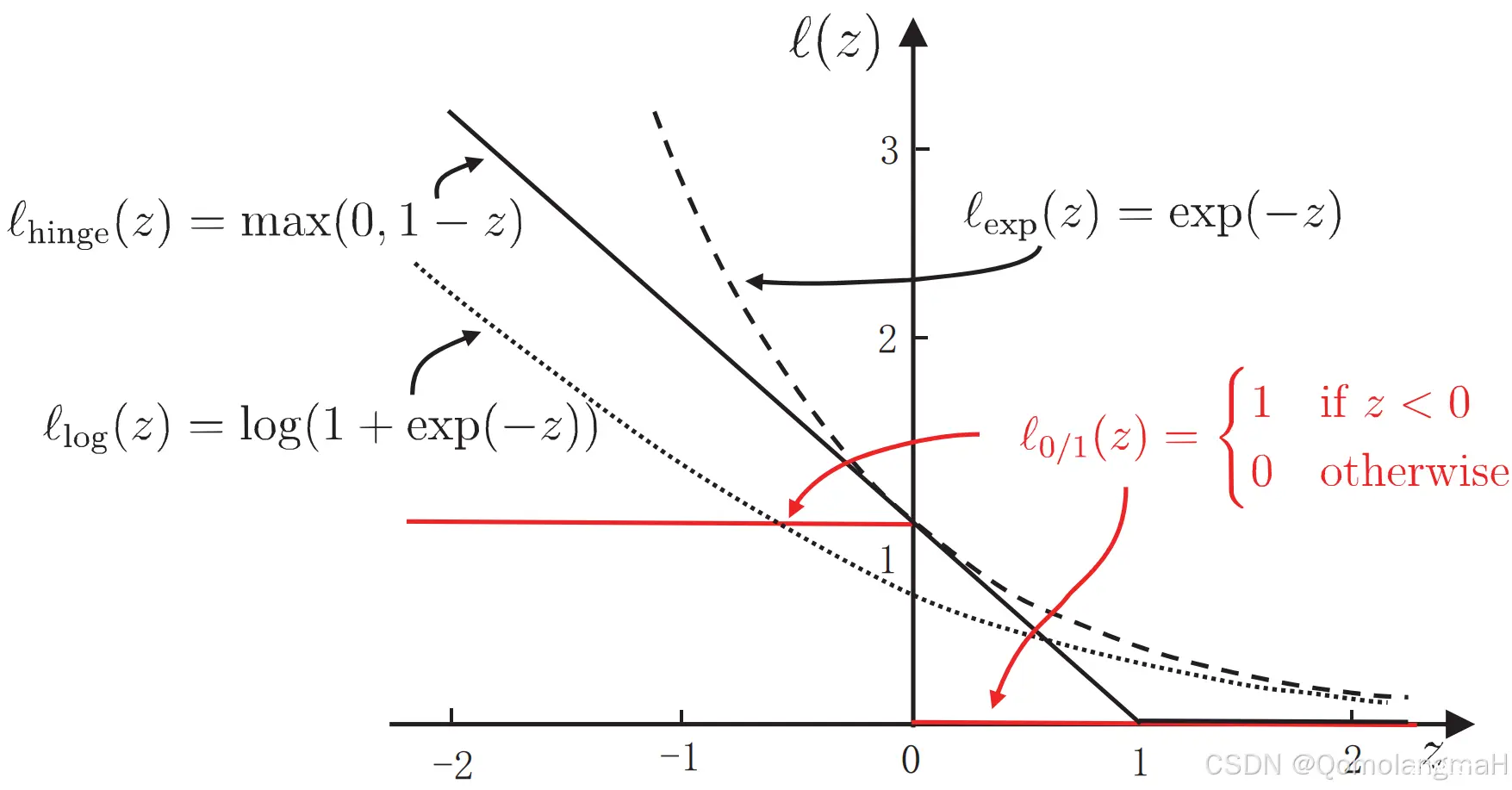
p.130, 式(6.31)-(6.33): 下标中"hinge",“exp”,“log” 斜体 --> 正体

p.131, 图 6.5: 修订文件

p.132, 倒数第7行: 下标中"log" 斜体 --> 正体

p.133, 式(6.42)加边注: “传统意义上的"结构风险"是指引入模型结构因素后的总体风险(或许更宜译为"带结构风险”), 本书则是指总体风险中直接对应于模型结构因素的部分, 这样从字面上更直观, 或有助于理解其与机器学习中其他内容间的联系. 参见p.160."

p.136, 式(6.54): 右边最后一项中的四处 “

i

i

i” -->; “

j

j

j”

p.136, 式(6.54): 右边最后一项中最后的 “

x

{\bm x}

x” --> “

x

i

{\bm x}_i

xi​”

第 7 章 贝叶斯分类器

p.152, 第三个式子等号右端: “

0.375

0.375

0.375” --> “

0.625

0.625

0.625”p.152, 第10行: “6/8 = 0.750” --> “5/8 = 0.625”p.153, 第3行: “

0.038

0.038

0.038” --> “

0.063

0.063

0.063”p.153, 第6行: “

0.038

0.038

0.038” --> “

0.063

0.063

0.063”p.153, 第3行: “0.063” --> “0.052”p.153, 第6行: “0.063” --> “0.052”p.156, 倒数第7行：“(7.23)” --> “(7.21)”p.156, 式(7.24)分母: “

N

i

N_i

Ni​” --> “N \times N_i”p.156, 式(7.25)下面一行: “其中

N

i

N_i

Ni​” --> “其中

N

N

N 是

D

D

D 中可能的类别数,

N

i

N_i

Ni​”p.156, 式(7.25)下面第4行, 分母: “

17

+

3

17+3

17+3” --> “

17

+

3

×

2

17 + 3 \times 2

17+3×2”p.156, 式(7.25)下面第4行: “0.350” --> “0.304”p.159, 第一行加边注：“一般需先对图剪枝, 仅保留有向图中~

x

x

x,

y

y

y,

z

\bf{z}

z~及它们的祖先结点”p.159, 倒数第5行: “Minimal” --> “Minimum”p.159, 倒数第9行、第10行中两处: “字节长度” --> “编码位数”p.160, 第1行、第4行中两处: “字节数” --> “编码位数”p.160, 第7行、第10行中两处: “字节” --> “编码位”p.160, 式(7.29)下面第2行: “需多少字节来描述

D

D

D” --> “对

D

D

D描述得有多好”；加边注: “可以从统计学习角度理解, 将两项分别视为结构风险和经验风险”p.168, 倒数第5行: “Jeff.” --> “J.”

第 8 章 集成学习

p.172, 式(8.2): “

H

H

H” --> “

F

F

F”p.173, 式(8.3): “

H

H

H” --> “

F

F

F”p.174, 图8.3最后一行: “

H

H

H” --> “

F

F

F”p.174, 式(8.7)中两处、(8.8)中 7 处、边注中两处: “

f

(

x

)

f(x)

f(x)” --> “

f

(

x

)

f(\bm{x})

f(x)”p.175, 式(8.12)前一行: “最小化” --> “最小化~

ℓ

e

x

p

(

H

t

−

1

+

α

t

h

t

∣

D

)

\ell_{\rm exp}(H_{t-1} + \alpha_t h_t \mid \mathcal{D})

ℓexp​(Ht−1​+αt​ht​∣D), 可简化为最小化”p.185, 式(8.28)前一行: “是” --> “定义为”p.187, 式(8.39)下面一行: “

≤

\le

≤” --> “

≥

\ge

≥”

第 9 章 聚类

p.198, 式(9.1)-(9.4): “

i

<

j

)

i<j)

i<j)” --> “

i

<

j

i<j

i<j”

p.199, 式(9.12)：分母的 “KaTeX parse error: Undefined control sequence: \miu at position 6: (\bm{\̲m̲i̲u̲}_i, \bm{\miu}_…” --> “

(

C

i

,

C

j

)

(C_i, C_j)

(Ci​,Cj​)”

p.203, 图9.2下面一行: “

x

27

\bm{x}_{27}

x27​” --> “

x

24

\bm{x}_{24}

x24​”

p.203, 图9.2下面第3行: “(0.532; 0.472)” --> “(0.478; 0.437)”

p.203, 图9.2下面第5行: “0.166” --> “0.220”

p.203, 图9.2下面第7行: 大括号中增加 “\bm{x}3", 去掉"\bm{x}{15}”

p.203, 倒数第5行: 大括号中去掉 “\bm{x}3", 增加"\bm{x}{15}”

p.203, 倒数第3行: “(0.473; 0.214)” --> “(0.493; 0.207)”

p.203, 倒数第3行: “(0.623; 0.388)” --> “(0.602; 0.396)”

p.204, 图9.3: 修订文件

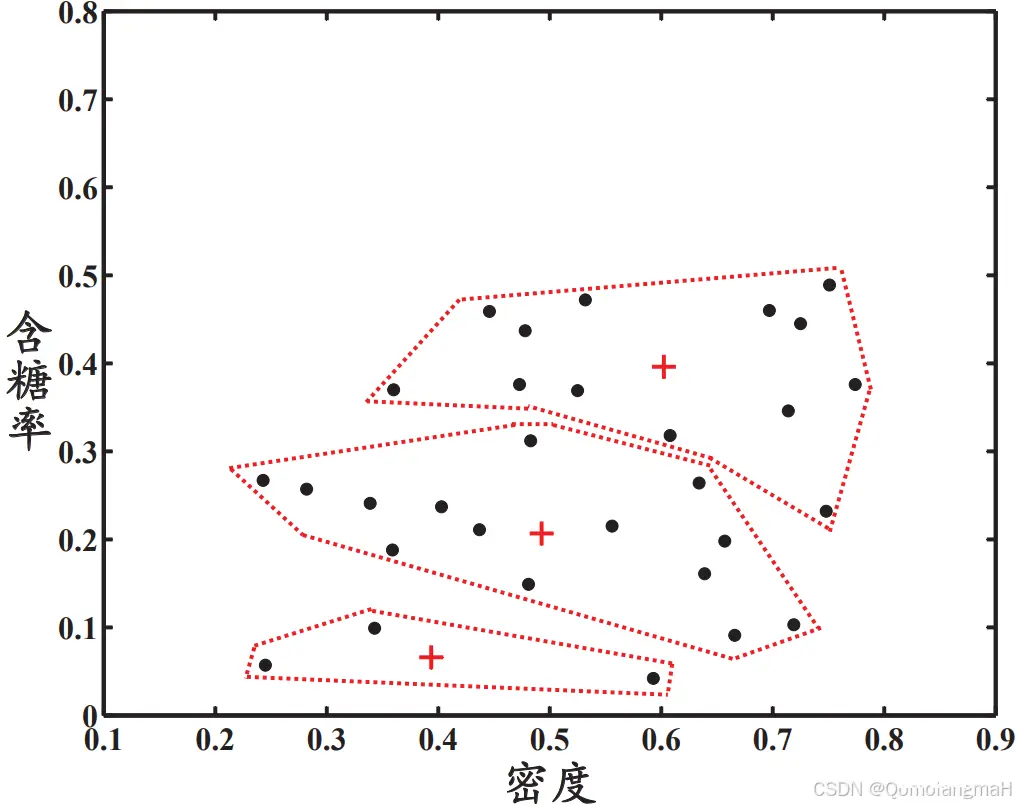
p.205, 图9.4第5行，

p

i

∗

p_{i^*}

pi∗​ -->

p

i

∗

\bm {p}_{i^*}

pi∗​p.206, 9.4.3节前倒数第5行: “

c

2

c_2

c2​” -->; “

c

1

c_1

c1​”p.206, 9.4.3节前倒数第2行: “(0.722; 0.442)” --> “(0.722; 0.447)”p.209, 式(9.38)上面一行: “样本” --> “混合成分”p.215, 图9.11第5步: “

j

=

1

,

2

,

…

,

m

j = 1, 2, \ldots, m

j=1,2,…,m” --> “

j

=

i

+

1

,

…

,

m

j = i+1, \ldots, m

j=i+1,…,m”p.220, 第6行: “

↦

\mapsto

↦” --> “

→

\to

→”,

第10章 降维与度量学习

p.230, 式(10.14)结尾: “.” --> “,”p.230, 式(10.14)下面一行开头顶格插入: “其中

W

=

(

w

1

,

w

2

,

…

,

w

d

)

{\bf W} = (\bm{w}_1, \bm{w}_2, \ldots, \bm{w}_d)

W=(w1​,w2​,…,wd​).”p.230, 式(10.15)上面一行加边注: “严格来说, 协方差矩阵是~

1

m

−

1

∑

i

=

1

m

x

i

x

i

T

{1 \over {m-1}}\sum\nolimits_{i=1}^m\bm{x}_i\bm{x}_i^{\rm T}

m−11​∑i=1m​xi​xiT​, 但前面的常数项在此不发生影响”p.230, 倒数第三行：“方差” --> “协方差矩阵”p.231, 式(10.17): 两处"

W

{\bf W}

W“–>”

w

i

{\bm w}_i

wi​", “

λ

\lambda

λ” --> “

λ

i

\lambda_i

λi​”p.231, 式(10.17)下面第二行: “

W

{\bf W}

W” --> “

W

∗

{\bf W}^*

W∗”p.231, 图10.5最后一行: “

W

{\bf W}

W” --> “

W

∗

{\bf W}^*

W∗”p.232, 第一行: “

W

{\bf W}

W” --> “

W

∗

{\bf W}^*

W∗”p.232, 式(10.19)前第二行: “

W

{\bf W}

W” --> “

W

=

(

w

1

,

w

2

,

…

,

w

d

)

{\bf W} = (\bm{w}_1, \bm{w}_2, \ldots, \bm{w}_d)

W=(w1​,w2​,…,wd​)”p.232, 式(10.19)前第二行: “即PCA欲求解” --> “则对于

w

j

\bm{w}_j

wj​, 由式(10.17)有”p.232, 式(10.19): 两处"

W

{\bf W}

W“–>”

w

j

{\bm w}_j

wj​"; “

λ

\lambda

λ” --> “

λ

j

\lambda_j

λj​”p.233, 式(10.20): 三处"

W

{\bf W}

W“–>”

w

j

{\bm w}_j

wj​"; 两处"

λ

\lambda

λ"–>“

λ

j

\lambda_j

λj​”; “

α

i

{\bm \alpha}_i

αi​”–>“

α

i

j

\alpha_i^j

αij​”p.233, 式(10.20)下一行: “

α

i

{\bm \alpha}_i

αi​”–>“

α

i

j

\alpha_i^j

αij​”; “

λ

\lambda

λ”–>“

λ

j

\lambda_j

λj​”; “

W

{\bf W}

W”–>“

w

j

{\bm w}_j

wj​”p.233, 式(10.20)下一行: “. 假定” --> “是

α

i

{\bm \alpha}_i

αi​的第

j

j

j个分量. 假定”p.233, 式(10.21): 两处"

W

{\bf W}

W“–>”

w

j

{\bm w}_j

wj​"; “

λ

\lambda

λ”–>“

λ

j

\lambda_j

λj​”p.233, 式(10.22): “

W

{\bf W}

W”–>“

w

j

{\bm w}_j

wj​”; “

α

i

{\bm \alpha}_i

αi​”–>“

α

i

j

\alpha_i^j

αij​”p.233, 式(10.24): 两处"

A

{\bf A}

A“–>”

α

j

{\bm \alpha}^j

αj"; “

λ

\lambda

λ”–>“

λ

j

\lambda_j

λj​”p.233, 式(10.24)下面一行: “

A

=

(

α

1

;

α

2

;

…

;

α

m

)

{\bf A} = ({\bm \alpha}_1; {\bm \alpha}_2; \ldots; {\bm \alpha}_m)

A=(α1​;α2​;…;αm​)” --> “

α

j

=

(

α

1

j

;

α

2

j

;

…

;

α

m

j

)

{\bm \alpha}^j = (\alpha_1^j; \alpha_2^j; \ldots; \alpha_m^j)

αj=(α1j​;α2j​;…;αmj​)”p.233, 式(10.25)下面一行: 去掉 “,

α

i

j

\alpha_i^j

αij​ 是

α

i

{\bm \alpha}_i

αi​ 的第

j

j

j 个分量”p.237, 图10.10第3行，“式(10.27)” --> “式(10.28)”p.239, 式(10.39)第二行式子: 去掉上标 “

2

2

2”p.240, 倒数第2段第1行: “Lapl-” --> “Lapla-”p.244, 第13行: “Locally” --> “Nonlinear dimensionality reduction by locally”p.244, 第14行: “2316” --> “2326”

第11章 特征选择与稀疏学习

p.249, 式(11.2): “

i

=

1

i=1

i=1” --> “

k

=

1

k=1

k=1”p.251, 倒数第6行: “当前特征子集~

A

A

A” --> “当前特征子集~

A

∗

A^*

A∗”p.253, 倒数第5行: “[Boyd and Vandenberghe, 2004]” --> “[Combettes and Wajs, 2005]”p.253, 式(11.9): 不等式两边的平方去掉p.256, 第4段: “固定住

α

i

{\bf \alpha}_i

αi​” --> “以

α

i

{\bf \alpha}_i

αi​为初值”p.256, 最后一段第1行: “

E

i

=

{\bf E}_i =

Ei​=” --> “${\bf E}_i = {\bf X} - $”p.263, 倒数第4行, 插入: “Combettes, P. L. and V. R. Wajs. (2005). ``Signal recovery by proximal forward-backward splitting.‘’ \textit{Mutiscale Modeling & Simulation}, 4(4):1168–1200.”

第12章 计算学习理论

p.269, 第3段倒数第2行: “

δ

\delta

δ” --> “

1

−

δ

1-\delta

1−δ”p.269, 最后一个边注倒数第3行: “

δ

\delta

δ” --> “

1

−

δ

1-\delta

1−δ”p.277, 式(12.29): “

E

(

h

)

−

E

^

(

h

)

E(h) - \hat{E}(h)

E(h)−E^(h)” --> “

∣

E

(

h

)

−

E

^

(

h

)

∣

\left| E(h) - \hat{E}(h) \right|

​E(h)−E^(h)

​”p.278, 倒数第4个式子，增加编号: “(12.33)”p.278, 倒数第2个式子，增加编号: “(12.35)”p.284, 倒数第3行：“

y

i

=

y_i =

yi​=” --> “

y

i

∈

y_i \in

yi​∈”p.286, 第2行: “

l

l

l” --> “

ℓ

\ell

ℓ”p.290, 倒数第8行: “, eds.” --> “.”

第13章 半监督学习

p.299, 式(13.9)后第三段第2行: “关于

D

u

D_u

Du​” --> “涉及

C

u

C_u

Cu​”p.301, 式(13.12)的下一行: “

(

f

l

T

f

u

T

)

T

({\bm f}_l^{\rm T}\,{\bm f}_u^{\rm T})^{\rm T}

(flT​fuT​)T” --> “

(

f

l

T

;

f

u

T

)

({\bm f}_l^{\rm T}; {\bm f}_u^{\rm T})

(flT​;fuT​)”p.301, 式(13.12)的下一行: “({\bm f}_l^{\rm T}; {\bm f}_u^{\rm T})

"

−

−

>

"

" --> "

"−−>"({\bm f}_l; {\bm f}_u)$”p.303, 式(13.20)：“\mapsto

"

−

−

>

"

" --> "

"−−>"\to$”p.303, 图13.5, 步骤10：“

y

i

y_i

yi​” --> “

y

^

i

\hat{y}_i

y^​i​”p.303, 倒数第二行：去掉 “[Zhou et al., 2004]”p.304, 第一行：“当” --> “考虑到有标记样本通常很少而未标记样本很多, 为缓解过拟合, 可在式(13.21)中引入针对未标记样本的_{L$_2$}范数项~

μ

∑

i

=

l

+

1

l

+

u

∥

F

i

∥

2

\mu \sum_{i=l+1}^{l+u}\|\mathbf{F}_{i}\|^{2}

μ∑i=l+1l+u​∥Fi​∥2, 在”; 同时插入边注: “参见_11.4节”p.307, 图13.7, 步骤11: “voilated” --> “violated”

第14章 概率图模型

p.320, 第8行：“其余~

n

−

2

n-2

n−2” --> “此前~

t

−

2

t-2

t−2”p.325, 第5行： “

x

V

∖

⟨

u

,

v

⟩

{\bf x}_{V \setminus \langle u, v\rangle}

xV∖⟨u,v⟩​” --> “

x

V

∖

{

u

,

v

}

{\bf x}_{V \setminus \{ u, v \}}

xV∖{ u,v}​”p.325, 第一个边注：“所有邻接变量” --> “父变量、子变量、子变量的其他父变量”p.327, 倒数第10至倒数第4行: 两处"[

P

P

P]" --> “[P]”, 4处"[

V

V

V]" --> “[V]”p.337, 14.6节第3段: 5_个"

N

N

N" --> “

d

d

d”p.338, 第2行加边注: “上一步中指派的_{$z_{t,n}$}是话题~

k

k

k”p.339, 式(14.41): “

i

i

i” --> “

k

k

k”; 两处~“

P

P

P” --> “

p

p

p”p.339, 式(14.41)下面一行: “

N

N

N” --> “

d

d

d”p.345, 倒数第6行： “2011” --> “2001”

第15章 规则学习

p.358, 倒数第6行：“LGG(

s

s

s,

t

t

t)” --> “

s

s

s,

t

t

t”

第16章 强化学习

p.372, 图16.2，所有"

s

s

s" --> “

x

x

x”p.372, 图16.2: 从"s=健康"到"s=溢水"的 “r=1” --> “r=-1”p.376, 图16.5的边注: “第 4 行中式(16.4)的参数” --> “该参数在第4行使用”p.384, 图16.10, 步骤9: “

π

(

x

,

a

)

\pi(x, a)

π(x,a)” --> “

π

(

x

)

\pi(x)

π(x)”p.385, 式(16.22): “

x

x

x” --> “

x

i

x_i

xi​”p.385, 式(16.25)和(16.26): 两处"

r

i

r_i

ri​" --> “

R

i

R_i

Ri​”p.385, 式(16.25)下一行: “若改用……” --> “其中

R

i

R_i

Ri​表示第

i

i

i条轨迹上自状态

x

x

x至结束的累积奖赏. 若改用……”p.385, 第二行: “在使用策略时并不需要

ϵ

−

\epsilon-

ϵ−贪心” --> “而不是为了最终使用”p.386, 式(16.28)下一行: “始终为1” --> “对于

a

i

=

π

(

x

i

)

a_i=\pi(x_i)

ai​=π(xi​)始终为1”p.386, 图16.11, 第4步: 两处 “

π

(

x

)

\pi(x)

π(x)” --> “

π

(

x

i

)

\pi(x_i)

π(xi​)”p.386, 图16.11, 第6步的式子 --> “

R

=

1

T

−

t

(

∑

i

=

t

+

1

T

r

i

)

∏

i

=

t

+

1

T

−

1

I

(

a

i

=

π

(

x

i

)

)

p

i

R=\frac{1}{T-t}\left(\sum_{i=t+1}^T r_i\right) \prod_{i=t+1}^{T-1} \frac{\mathbb I(a_i=\pi(x_i))}{p_i}

R=T−t1​(∑i=t+1T​ri​)∏i=t+1T−1​pi​I(ai​=π(xi​))​”p.386, 图16.11, 边注"计算修正的累积奖赏." --> “计算修正的累积奖赏. 连乘内下标大于上标的项取值为1.”; 去掉边注"重要性采样系数."p.387, 倒数第二行: “

ϵ

−

\epsilon-

ϵ−贪心策略, 而执行(第5行)的是原始策略” --> “原始策略, 而执行(第4行)的是

ϵ

−

\epsilon-

ϵ−贪心策略”p.388, 图16.13, 步骤4: “

π

ϵ

(

x

)

\pi^{\epsilon}(x)

πϵ(x)” --> “

a

=

π

ϵ

(

x

)

a = \pi^{\epsilon}(x)

a=πϵ(x)”p.388, 图16.13, 步骤8: 去掉",

a

=

a

′

a = a'

a=a′"p.393, 第四段第一行: 去掉 “[Kuleshov and Precup, 2000]和”p.393, 边注第1行：“后悔” --> “遗憾”p.393, 第4段第4行：“悔界” --> “遗憾界”p.395, 去掉最后一行p.396, 去掉第一行

附 录

p.399, 式(A.9): “

A

1

σ

n

A_{1 \sigma n}

A1σn​” --> “

A

n

σ

n

A_{n \sigma n}

Anσn​”p.400, 第1行: “(1,4,3,2)” --> “(3,1,2)”p.402, 式(A.32)最后一行的式子中: “

2

A

2{\mathbf A}

2A” --> “

2

A

T

2{\mathbf A}^{\rm T}

2AT”p.402, 式(A.32)加边注: “机器学习中

W

\bf W

W 通常是对称矩阵”p.403, 第5行: “k” 正体 --> 斜体p.404, 式(B.3)最后一行的式子 --> “

λ

g

(

x

)

=

0

\lambda g({\bm x})=0

λg(x)=0”p.405, 边注第2行: “乘子” --> “函数”p.406, 第10行：“再并令” --> “再令”p.415, 5处"字节数" --> “比特数”p.417, 第3段第1行: “通往人工智能的途径” --> “一种人工智能途径”

按时间排序

(第一版第45次印刷, 2024年1月):

p.123, 倒数第三行，“即可将

L

(

w

,

b

,

α

)

L(w,b,\alpha)

L(w,b,α)中的

w

w

w和

b

b

b消去，再考虑式(6.10)的约束，就得到式(6.6)的对偶问题：”–> “考虑式(6.10)的约束，即可将

L

(

w

,

b

,

α

)

L(w,b,\alpha)

L(w,b,α)中的

w

w

w和

b

b

b消去，得到式(6.6)的对偶问题：”p.205, 图9.4第5行，

p

i

∗

p_{i^*}

pi∗​ -->

p

i

∗

\bm {p}_{i^*}

pi∗​p.237, 图10.10第3行，“式(10.27)” --> “式(10.28)”

(第一版第40次印刷, 2022年11月):

p.39, 第1行，“大于” --> “小于”

(第一版第36次印刷, 2021年5月):

p.38, 式(2.27),

ϵ

0

×

m

\epsilon_0 \times m

ϵ0​×m -->

ϵ

×

m

\epsilon \times m

ϵ×mp.38, 式(2.27),

ϵ

i

(

1

−

ϵ

)

m

−

i

\epsilon^{i} (1-\epsilon)^{m-i}

ϵi(1−ϵ)m−i -->

ϵ

0

i

(

1

−

ϵ

0

)

m

−

i

\epsilon_0^{i} (1-\epsilon_0)^{m-i}

ϵ0i​(1−ϵ0​)m−i

(第一版第35次印刷, 2020年11月):

p.59, 倒数第二行：“其第_$t+1$轮”–>“从当前_$\bm\beta$生成下一轮”p.59, 式(3.29):

β

t

+

1

\bm\beta^{t+1}

βt+1 -->

β

′

\bm\beta^{'}

β′,

β

t

\bm\beta^{t}

βt -->

β

\bm\beta

βp.325, 第5行： “

x

V

∖

⟨

u

,

v

⟩

{\bf x}_{V \setminus \langle u, v\rangle}

xV∖⟨u,v⟩​” --> “

x

V

∖

{

u

,

v

}

{\bf x}_{V \setminus \{ u, v \}}

xV∖{ u,v}​”p.327, 倒数第10至倒数第4行: 两处"[

P

P

P]" --> “[P]”, 4处"[

V

V

V]" --> “[V]”p.337, 14.6节第3段: 5_个"

N

N

N" --> “

d

d

d”p.338, 第2行加边注: “上一步中指派的_{$z_{t,n}$}是话题~

k

k

k”p.339, 式(14.41): “

i

i

i” --> “

k

k

k”; 两处~“

P

P

P” --> “

p

p

p”p.339, 式(14.41)下面一行: “

N

N

N” --> “

d

d

d”p.345, 倒数第6行： “2011” --> “2001”p.372, 图16.2，所有"

s

s

s" --> “

x

x

x”p.415, 5处"字节数" --> “比特数”

(第一版第34次印刷, 2020年7月):

p.10, 倒数第7行: “Nilson” --> “Nilsson”p.41, 式(2.32)的下一行: “自由度为~5” --> “自由度为~4”; “2.5706” --> “2.776”; “2.0150” --> “2.132”p.112, 式(5.24): 两处"

⊤

^{\top}

⊤" --> “

T

^{\rm T}

T”p.159, 倒数第5行: “Minimal” --> “Minimum”p.168, 倒数第5行: “Jeff.” --> “J.”p.220, 第6行: “

↦

\mapsto

↦” --> “

→

\to

→”,p.240, 倒数第2段第1行: “Lapl-” --> “Lapla-”p.251, 倒数第6行: “当前特征子集~

A

A

A” --> “当前特征子集~

A

∗

A^*

A∗”p.253, 式(11.9): 不等式两边的平方去掉p.278, 倒数第4个式子，增加编号: “(12.33)”p.278, 倒数第2个式子，增加编号: “(12.35)”p.286, 第2行: “

l

l

l” --> “

ℓ

\ell

ℓ”p.290, 倒数第8行: “, eds.” --> “.”p.301, 式(13.12)的下一行: “({\bm f}_l^{\rm T}; {\bm f}_u^{\rm T})

"

−

−

>

"

" --> "

"−−>"({\bm f}_l; {\bm f}_u)$”p.303, 式(13.20)：“\mapsto

"

−

−

>

"

" --> "

"−−>"\to$”p.303, 图13.5, 步骤10：“

y

i

y_i

yi​” --> “

y

^

i

\hat{y}_i

y^​i​”p.307, 图13.7, 步骤11: “voilated” --> “violated”p.325, 第一个边注：“所有邻接变量” --> “父变量、子变量、子变量的其他父变量”p.358, 倒数第6行：“LGG(

s

s

s,

t

t

t)” --> “

s

s

s,

t

t

t”p.393, 边注第1行：“后悔” --> “遗憾”p.393, 第4段第4行：“悔界” --> “遗憾界”p.403, 第5行: “k” 正体 --> 斜体p.405, 边注第2行: “乘子” --> “函数”

(第一版第33次印刷, 2020年4月):

p.31, 图 2.3: 修订文件p.130, 式(6.31)-(6.33): 下标中"hinge",“exp”,“log” 斜体 --> 正体p.132, 倒数第7行: 下标中"log" 斜体 --> 正体p.198, 式(9.1)-(9.4): “

i

<

j

)

i<j)

i<j)” --> “

i

<

j

i<j

i<j”p.269, 第3段倒数第2行: “

δ

\delta

δ” --> “

1

−

δ

1-\delta

1−δ”p.269, 最后一个边注倒数第3行: “

δ

\delta

δ” --> “

1

−

δ

1-\delta

1−δ”

(第一版第31次印刷, 2019年9月):

p.38, 式(2.27)：“

max

⁡

\max

max” --> “

min

⁡

\min

min”p.39, 倒数第1行: “若平均错误率……临界值范围” --> “若_{$\tao_t$}位于临界值范围”p.152, 第10行: “6/8 = 0.750” --> “5/8 = 0.625”p.153, 第3行: “0.063” --> “0.052”p.153, 第6行: “0.063” --> “0.052”p.172, 式(8.2): “

H

H

H” --> “

F

F

F”p.173, 式(8.3): “

H

H

H” --> “

F

F

F”p.174, 图8.3最后一行: “

H

H

H” --> “

F

F

F”p.175, 式(8.12)前一行: “最小化” --> “最小化~

ℓ

e

x

p

(

H

t

−

1

+

α

t

h

t

∣

D

)

\ell_{\rm exp}(H_{t-1} + \alpha_t h_t \mid \mathcal{D})

ℓexp​(Ht−1​+αt​ht​∣D), 可简化为最小化”p.185, 式(8.28)前一行: “是” --> “定义为”p.284, 倒数第3行：“

y

i

=

y_i =

yi​=” --> “

y

i

∈

y_i \in

yi​∈”p.385, 式(16.22): “

x

x

x” --> “

x

i

x_i

xi​”p.406, 第10行：“再并令” --> “再令”

(第一版第27次印刷, 2018年6月):

p.42, 表2.5后第四行：“

(

k

2

−

1

)

/

12

(k^2-1)/12

(k2−1)/12” --> “

(

k

2

−

1

)

/

12

N

(k^2-1)/12N

(k2−1)/12N”p.159, 倒数第9行、第10行中两处: “字节长度” --> “编码位数”p.160, 第1行、第4行中两处: “字节数” --> “编码位数”p.160, 第7行、第10行中两处: “字节” --> “编码位”p.174, 式(8.7)中两处、(8.8)中 7 处、边注中两处: “

f

(

x

)

f(x)

f(x)” --> “

f

(

x

)

f(\bm{x})

f(x)”

(第一版第26次印刷, 2018年5月):

p.58, 倒数第二行：“对率函数” --> “下面我们会看到, 对率回归求解的目标函数”p.230, 倒数第三行：“方差” --> “协方差矩阵”

(第一版第25次印刷, 2018年3月):

p.39, 最后一行：“

[

−

∞

,

[-\infty,

[−∞,” --> “

(

−

∞

,

(-\infty,

(−∞,”，“

,

∞

]

, \infty]

,∞]” --> “

,

∞

)

, \infty)

,∞)”p.199, 式(9.12)：分母的 “KaTeX parse error: Undefined control sequence: \miu at position 6: (\bm{\̲m̲i̲u̲}_i, \bm{\miu}_…” --> “

(

C

i

,

C

j

)

(C_i, C_j)

(Ci​,Cj​)”

(第一版第24次印刷, 2018年1月):

p.112, 图 5.14a: 修订文件p.303, 倒数第二行：去掉 “[Zhou et al., 2004]”p.304, 第一行：“当” --> “考虑到有标记样本通常很少而未标记样本很多, 为缓解过拟合, 可在式(13.21)中引入针对未标记样本的_{L$_2$}范数项~

μ

∑

i

=

l

+

1

l

+

u

∥

F

i

∥

2

\mu \sum_{i=l+1}^{l+u}\|\mathbf{F}_{i}\|^{2}

μ∑i=l+1l+u​∥Fi​∥2, 在”; 同时插入边注: “参见_11.4节”

(第一版第23次印刷, 2017年10月):

p.27, 式(2.1)：第一个"

↦

\mapsto

↦" --> “

→

\to

→”, 第二个"

↦

\mapsto

↦" --> “

=

=

=”p.80, 倒数第2行：“算法4.2” --> “图 4.2 算法”p.131, 图 6.5: 修订文件

(第一版第22次印刷, 2017年9月):

p.156, 倒数第7行：“(7.23)” --> “(7.21)”p.320, 第8行：“其余~

n

−

2

n-2

n−2” --> “此前~

t

−

2

t-2

t−2”

(第一版第21次印刷, 2017年8月)

(第一版第20次印刷, 2017年7月):

p.60, 图3.3中：“

y

=

w

T

x

y = \bm{w}^{\rm T}\bm{x}

y=wTx,

y

y

y” --> “投影方向~

w

\bm{w}

w”p.133, 式(6.42)加边注: “传统意义上的"结构风险"是指引入模型结构因素后的总体风险(或许更宜译为"带结构风险”), 本书则是指总体风险中直接对应于模型结构因素的部分, 这样从字面上更直观, 或有助于理解其与机器学习中其他内容间的联系. 参见p.160."

(第一版第19次印刷, 2017年6月):

p.159, 第一行加边注：“一般需先对图剪枝, 仅保留有向图中~

x

x

x,

y

y

y,

z

\bf{z}

z~及它们的祖先结点”p.230, 式(10.15)上面一行加边注: “严格来说, 协方差矩阵是~

1

m

−

1

∑

i

=

1

m

x

i

x

i

T

{1 \over {m-1}}\sum\nolimits_{i=1}^m\bm{x}_i\bm{x}_i^{\rm T}

m−11​∑i=1m​xi​xiT​, 但前面的常数项在此不发生影响”

(第一版第18次印刷, 2017年5月):

p.187, 式(8.39)下面一行: “

≤

\le

≤” --> “

≥

\ge

≥”

(第一版第17次印刷, 2017年4月):

p.384, 图16.10, 步骤9: “

π

(

x

,

a

)

\pi(x, a)

π(x,a)” --> “

π

(

x

)

\pi(x)

π(x)”p.388, 图16.13, 步骤4: “

π

ϵ

(

x

)

\pi^{\epsilon}(x)

πϵ(x)” --> “

a

=

π

ϵ

(

x

)

a = \pi^{\epsilon}(x)

a=πϵ(x)”p.388, 图16.13, 步骤8: 去掉",

a

=

a

′

a = a'

a=a′"

(第一版第16次印刷, 2017年3月):

p.417, 第3段第1行: “通往人工智能的途径” --> “一种人工智能途径”

(第一版第15次印刷, 2017年2月):

p.206, 9.4.3节前倒数第5行: “

c

2

c_2

c2​” --> “

c

1

c_1

c1​”

(第一版第14次印刷, 2016年12月):

p.34, 图 2.4(b): 修订文件p.206, 9.4.3节前倒数第2行: “(0.722; 0.442)” --> “(0.722; 0.447)”p.209, 式(9.38)上面一行: “样本” --> “混合成分”p.215, 图9.11第5步: “

j

=

1

,

2

,

…

,

m

j = 1, 2, \ldots, m

j=1,2,…,m” --> “

j

=

i

+

1

,

…

,

m

j = i+1, \ldots, m

j=i+1,…,m”p.230, 式(10.14)结尾: “.” --> “,”p.230, 式(10.14)下面一行开头顶格插入: “其中

W

=

(

w

1

,

w

2

,

…

,

w

d

)

{\bf W} = (\bm{w}_1, \bm{w}_2, \ldots, \bm{w}_d)

W=(w1​,w2​,…,wd​).”p.231, 式(10.17): 两处"

W

{\bf W}

W“–>”

w

i

{\bm w}_i

wi​", “

λ

\lambda

λ” --> “

λ

i

\lambda_i

λi​”p.231, 式(10.17)下面第二行: “

W

{\bf W}

W” --> “

W

∗

{\bf W}^*

W∗”p.231, 图10.5最后一行: “

W

{\bf W}

W” --> “

W

∗

{\bf W}^*

W∗”p.232, 第一行: “

W

{\bf W}

W” --> “

W

∗

{\bf W}^*

W∗”p.232, 式(10.19)前第二行: “

W

{\bf W}

W” --> “

W

=

(

w

1

,

w

2

,

…

,

w

d

)

{\bf W} = (\bm{w}_1, \bm{w}_2, \ldots, \bm{w}_d)

W=(w1​,w2​,…,wd​)”p.232, 式(10.19)前第二行: “即PCA欲求解” --> “则对于

w

j

\bm{w}_j

wj​, 由式(10.17)有”p.232, 式(10.19): 两处"

W

{\bf W}

W“–>”

w

j

{\bm w}_j

wj​"; “

λ

\lambda

λ” --> “

λ

j

\lambda_j

λj​”p.233, 式(10.20): 三处"

W

{\bf W}

W“–>”

w

j

{\bm w}_j

wj​"; 两处"

λ

\lambda

λ"–>“

λ

j

\lambda_j

λj​”; “

α

i

{\bm \alpha}_i

αi​”–>“

α

i

j

\alpha_i^j

αij​”p.233, 式(10.20)下一行: “

α

i

{\bm \alpha}_i

αi​”–>“

α

i

j

\alpha_i^j

αij​”; “

λ

\lambda

λ”–>“

λ

j

\lambda_j

λj​”; “

W

{\bf W}

W”–>“

w

j

{\bm w}_j

wj​”p.233, 式(10.20)下一行: “. 假定” --> “是

α

i

{\bm \alpha}_i

αi​的第

j

j

j个分量. 假定”p.233, 式(10.21): 两处"

W

{\bf W}

W“–>”

w

j

{\bm w}_j

wj​"; “

λ

\lambda

λ”–>“

λ

j

\lambda_j

λj​”p.233, 式(10.22): “

W

{\bf W}

W”–>“

w

j

{\bm w}_j

wj​”; “

α

i

{\bm \alpha}_i

αi​”–>“

α

i

j

\alpha_i^j

αij​”p.233, 式(10.24): 两处"

A

{\bf A}

A“–>”

α

j

{\bm \alpha}^j

αj"; “

λ

\lambda

λ”–>“

λ

j

\lambda_j

λj​”p.233, 式(10.24)下面一行: “

A

=

(

α

1

;

α

2

;

…

;

α

m

)

{\bf A} = ({\bm \alpha}_1; {\bm \alpha}_2; \ldots; {\bm \alpha}_m)

A=(α1​;α2​;…;αm​)” --> “

α

j

=

(

α

1

j

;

α

2

j

;

…

;

α

m

j

)

{\bm \alpha}^j = (\alpha_1^j; \alpha_2^j; \ldots; \alpha_m^j)

αj=(α1j​;α2j​;…;αmj​)”p.233, 式(10.25)下面一行: 去掉 “,

α

i

j

\alpha_i^j

αij​ 是

α

i

{\bm \alpha}_i

αi​ 的第

j

j

j 个分量”

(第一版第13次印刷, 2016年11月):

p.36, 倒数第5行: “(TPR, FPR)” --> “(FPR, TPR)”p.120, 第7行: “(1927 – )” --> “(1927 – 2016)”p.203, 图9.2下面一行: “

x

27

\bm{x}_{27}

x27​” --> “

x

24

\bm{x}_{24}

x24​”p.203, 图9.2下面第3行: “(0.532; 0.472)” --> “(0.478; 0.437)”p.203, 图9.2下面第5行: “0.166” --> “0.220”p.203, 图9.2下面第7行: 大括号中增加 “\bm{x}3", 去掉"\bm{x}{15}”p.203, 倒数第5行: 大括号中去掉 “\bm{x}3", 增加"\bm{x}{15}”p.203, 倒数第3行: “(0.473; 0.214)” --> “(0.493; 0.207)”p.203, 倒数第3行: “(0.623; 0.388)” --> “(0.602; 0.396)”p.204, 图9.3: 修订文件

(第一版第10次印刷, 2016年9月)：

p.156, 式(7.24)分母: “

N

i

N_i

Ni​” --> “N \times N_i”p.156, 式(7.25)下面一行: “其中

N

i

N_i

Ni​” --> “其中

N

N

N 是

D

D

D 中可能的类别数,

N

i

N_i

Ni​”p.156, 式(7.25)下面第4行, 分母: “

17

+

3

17+3

17+3” --> “

17

+

3

×

2

17 + 3 \times 2

17+3×2”p.156, 式(7.25)下面第4行: “0.350” --> “0.304”

(第一版第9次印刷, 2016年8月)

(第一版第8次印刷, 2016年5月)：

p.5, 第2段倒数第3行: “3、2、2” --> “3、3、3”p.5, 第2段倒数第2行: “

4

×

3

×

3

+

1

=

37

4 \times 3 \times 3 + 1 = 37

4×3×3+1=37” --> “

4

×

4

×

4

+

1

=

65

4 \times 4 \times 4 + 1 = 65

4×4×4+1=65”p.26, 边注第2行: “2.6 节” --> “2.5 节”p.41, 式(2.33)上面一行: “正态分布, 且均值 …… 因此变量” --> “正态分布. McNemar检验考虑变量”p.41, 式(2.33)旁加边注: “

e

01

+

e

10

e_{01} + e_{10}

e01​+e10​ 通常很小, 需考虑连续性校正, 因此分子中有

−

1

-1

−1 项”p.45, 第一个边注: “由式(2.37)” --> “考虑到噪声不依赖于

f

f

f, 由式(2.37)”p.63, 式(3.45)下面一行: “

N

−

1

N-1

N−1个最大” --> “

d

′

d'

d′个最大非零”p.63, 式(3.45)下面第2行: “矩阵.” --> “矩阵,

d

′

≤

N

−

1

d'\le N-1

d′≤N−1.”; 加边注: “最多有

N

−

1

N-1

N−1个非零特征值”p.63, 式(3.45)下面第3行: “

N

−

1

N-1

N−1维” --> “

d

′

d'

d′维”p.63, 式(3.45)下面第4行: “

N

−

1

N-1

N−1通常远小于数据原有的属性数” --> “

d

′

d'

d′通常远小于数据原有的属性数

d

d

d”p.100, 图5.5, 左图最上面的 “阈值

0.5

0.5

0.5” --> “阈值

1.5

1.5

1.5”p.100, 图5.5, 左图最右边的 “阈值

0.5

0.5

0.5” --> “阈值

−

1.5

-1.5

−1.5”p.100, 图5.5, 左图中间的"1 -1 -1 1" --> “1 1 -1 -1”p.125, 式(6.18): “

y

s

y_s

ys​” --> “

1

/

y

s

1/y_s

1/ys​”p.136, 式(6.54): 右边最后一项中的四处 “

i

i

i” --> “

j

j

j”p.136, 式(6.54): 右边最后一项中最后的 “

x

{\bm x}

x” --> “

x

i

{\bm x}_i

xi​”p.152, 第三个式子等号右端: “

0.375

0.375

0.375” --> “

0.625

0.625

0.625”p.153, 第3行: “

0.038

0.038

0.038” --> “

0.063

0.063

0.063”p.153, 第6行: “

0.038

0.038

0.038” --> “

0.063

0.063

0.063”p.160, 式(7.29)下面第2行: “需多少字节来描述

D

D

D” --> “对

D

D

D描述得有多好”；加边注: “可以从统计学习角度理解, 将两项分别视为结构风险和经验风险”p.239, 式(10.39)第二行式子: 去掉上标 “

2

2

2”p.244, 第13行: “Locally” --> “Nonlinear dimensionality reduction by locally”p.244, 第14行: “2316” --> “2326”p.249, 式(11.2): “

i

=

1

i=1

i=1” --> “

k

=

1

k=1

k=1”p.253, 倒数第5行: “[Boyd and Vandenberghe, 2004]” --> “[Combettes and Wajs, 2005]”p.263, 倒数第4行, 插入: “Combettes, P. L. and V. R. Wajs. (2005). ``Signal recovery by proximal forward-backward splitting.‘’ \textit{Mutiscale Modeling & Simulation}, 4(4):1168–1200.”p.277, 式(12.29): “

E

(

h

)

−

E

^

(

h

)

E(h) - \hat{E}(h)

E(h)−E^(h)” --> “

∣

E

(

h

)

−

E

^

(

h

)

∣

\left| E(h) - \hat{E}(h) \right|

​E(h)−E^(h)

​”p.299, 式(13.9)后第三段第2行: “关于

D

u

D_u

Du​” --> “涉及

C

u

C_u

Cu​”

(第一版第7次印刷, 2016年4月)：

p.42, 表2.5下面一段的第三行: “服从正态分布，其均值” --> “的均值”p.42, 倒数第二行加边注: “原始检验要求

k

k

k较大(例如

>

30

>30

>30)，若

k

k

k较小则倾向于认为无显著区别”

(第一版第6次印刷, 2016年4月)：

p.56, 图3.1中，红色第一和第二个点的坐标互换p.114, 图5.15中, 卷积层 16@10x10 和 采样层 16@5x5 各去掉 8 个方块p.301, 式(13.12)的下一行: “

(

f

l

T

f

u

T

)

T

({\bm f}_l^{\rm T}\,{\bm f}_u^{\rm T})^{\rm T}

(flT​fuT​)T” --> “

(

f

l

T

;

f

u

T

)

({\bm f}_l^{\rm T}; {\bm f}_u^{\rm T})

(flT​;fuT​)”p.372, 图16.2: 从"s=健康"到"s=溢水"的 “r=1” --> “r=-1”p.376, 图16.5的边注: “第 4 行中式(16.4)的参数” --> “该参数在第4行使用”p.385, 第二行: “在使用策略时并不需要

ϵ

−

\epsilon-

ϵ−贪心” --> “而不是为了最终使用”p.387, 倒数第二行: “

ϵ

−

\epsilon-

ϵ−贪心策略, 而执行(第5行)的是原始策略” --> “原始策略, 而执行(第4行)的是

ϵ

−

\epsilon-

ϵ−贪心策略”p.393, 第四段第一行: 去掉 “[Kuleshov and Precup, 2000]和”p.395, 去掉最后一行p.396, 去掉第一行p.402, 式(A.32)加边注: “机器学习中

W

\bf W

W 通常是对称矩阵”

(第一版第5次印刷, 2016年3月)：

p.62, 第1行加边注: “

(

μ

0

−

μ

1

)

T

w

(\bm{\mu}_0 - \bm{\mu}_1)^{\rm T} \bm{w}

(μ0​−μ1​)Tw 是标量”p.78, 图4.4, 从右往左数: 第二个叶结点改为“好瓜”，第三个叶结点改为“坏瓜”p.85, 图4.8, 从右往左数: 第二个叶结点改为“好瓜”，第三个叶结点改为“坏瓜”p.85, 图4.8, 中间分支底层: “硬挺”–> “硬滑”p.89, 图4.9, 中间分支底层: “硬挺”–> “硬滑”p.103, 最后一行的式子: 求和的"

q

q

q" --> “

l

l

l”p.399, 式(A.9): “

A

1

σ

n

A_{1 \sigma n}

A1σn​” --> “

A

n

σ

n

A_{n \sigma n}

Anσn​”p.400, 第1行: “(1,4,3,2)” --> “(3,1,2)”p.402, 式(A.32)最后一行的式子中: “

2

A

2{\mathbf A}

2A” --> “

2

A

T

2{\mathbf A}^{\rm T}

2AT”

(第一版第4次印刷, 2016年3月)：

p.59, 式(3.27)加边注: “考虑

y

i

∈

{

0

,

1

}

y_i \in \{0, 1\}

yi​∈{ 0,1}”

(第一版第3次印刷, 2016年3月)：

p.15, 第5行: “居功” --> “厥功”p.55, 最后一行: 式子括号中的逗号改为分号p.125, 第3行: “减小” --> “增大”p.125, 第4行，第6行: “减幅” --> “增幅”p.125, 第5行: “减小” --> “增长”

(第一版第2次印刷, 2016年2月)：

p.38, 第6行: “

ϵ

m

′

\epsilon^{m'}

ϵm′” --> “

(

m

m

′

)

ϵ

m

′

{m \choose m'} \epsilon^{m'}

(m′m​)ϵm′”p.119, 第14行: “318–362” --> “533–536”p.404, 式(B.3)最后一行的式子 --> “

λ

g

(

x

)

=

0

\lambda g({\bm x})=0

λg(x)=0”

(第一版第1次印刷, 2016年1月)：

p.6, 图1.2: 图中两处"清脆" --> “浊响”p.28, 第3段倒数第2行: “大量” --> “不少”p.28, 边注: “例如 ……上百亿个参数” --> “机器学习常涉及两类参数: 一类是算法的参数, 亦称"超参数”, 数目常在10以内; 另一类是模型的参数, 数目可能很多, 例如……上百亿个参数. 两者调参方式相似, 均是产生多个模型之后基于某种评估方法来进行选择; 不同之处在于前者通常是由人工设定多个参数候选值后产生模型, 后者则是通过学习来产生多个候选模型(例如神经网络在不同轮数停止训练)."p.31, 倒数第3行: “Event” --> “Even”p.256, 第4段: “固定住

α

i

{\bf \alpha}_i

αi​” --> “以

α

i

{\bf \alpha}_i

αi​为初值”p.256, 最后一段第1行: “

E

i

=

{\bf E}_i =

Ei​=” --> “${\bf E}_i = {\bf X} - $”p.385, 式(16.25)和(16.26): 两处"

r

i

r_i

ri​" --> “

R

i

R_i

Ri​”p.385, 式(16.25)下一行: “若改用……” --> “其中

R

i

R_i

Ri​表示第

i

i

i条轨迹上自状态

x

x

x至结束的累积奖赏. 若改用……”p.386, 式(16.28)下一行: “始终为1” --> “对于

a

i

=

π

(

x

i

)

a_i=\pi(x_i)

ai​=π(xi​)始终为1”p.386, 图16.11, 第4步: 两处 “

π

(

x

)

\pi(x)

π(x)” --> “

π

(

x

i

)

\pi(x_i)

π(xi​)”p.386, 图16.11, 第6步的式子 --> “

R

=

1

T

−

t

(

∑

i

=

t

+

1

T

r

i

)

∏

i

=

t

+

1

T

−

1

I

(

a

i

=

π

(

x

i

)

)

p

i

R=\frac{1}{T-t}\left(\sum_{i=t+1}^T r_i\right) \prod_{i=t+1}^{T-1} \frac{\mathbb I(a_i=\pi(x_i))}{p_i}

R=T−t1​(∑i=t+1T​ri​)∏i=t+1T−1​pi​I(ai​=π(xi​))​”p.386, 图16.11, 边注"计算修正的累积奖赏." --> “计算修正的累积奖赏. 连乘内下标大于上标的项取值为1.”; 去掉边注"重要性采样系数."