前言 

文章概述《深度学习详解》- 1.1

书中介绍了机器学习的基本概念及其应用，包括回归、分类和结构化学习。通过对视频点击次数预测案例的学习，阐述了机器学习的三个步骤：构建模型、定义损失函数以及使用梯度下降法寻找最优参数。作者详细解释了如何通过未知参数来预测特定变量的值，并通过计算损失函数来评估模型的准确性。此外，讨论了梯度下降算法的工作原理及潜在问题，如局部最小值的存在。最后，文中展示了如何使用线性模型并结合梯度下降法来优化模型参数，从而提高预测精度。通过这个实例，读者能够理解机器学习的核心理念和实践方法。

个人学习笔记以及概念梳理，望对大家有所帮助。

思维导图1.1

机器学习的主要任务类型（补充）

涉及的一些术语

涉及到的一些公式

 

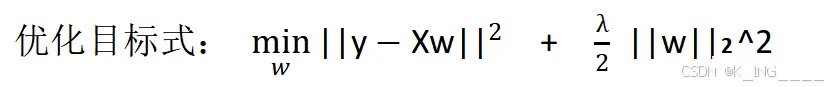
学习过程遇到的一些问题的理解：

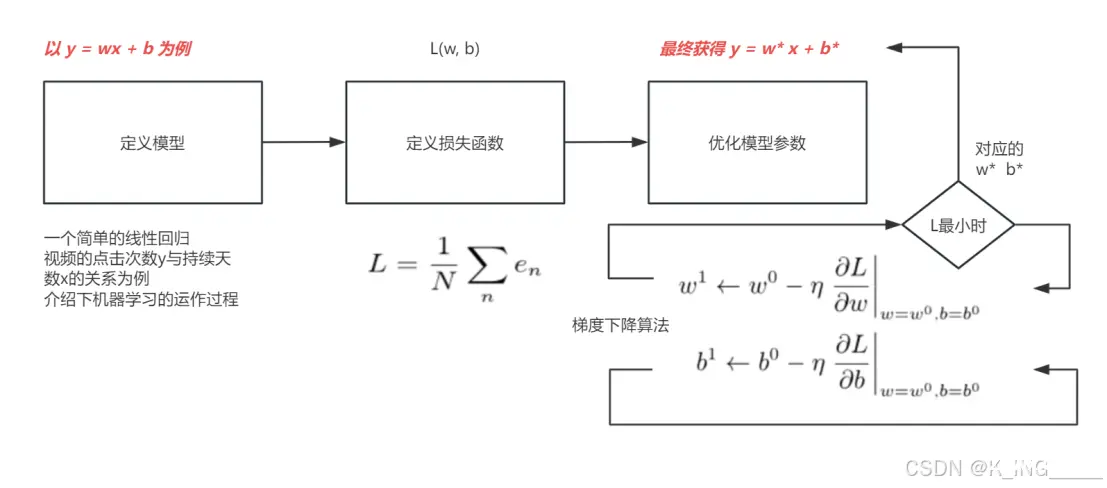
1机器学习找函数的过程可以总结为以下三个步骤

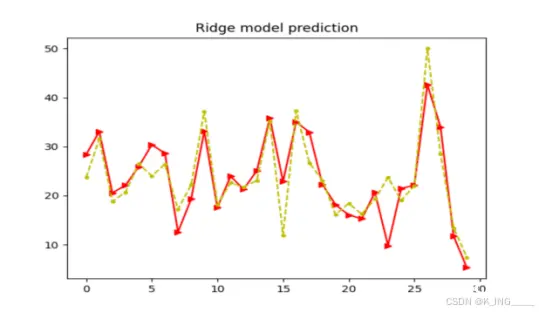
1）定义模型：选择一个包含未知参数的函数（模型），该函数能够预测输出。例如，在预测视频点击次数的例子中，模型被定义为 y=b+wx ，其中 y 是预测的观看次数，x 是前一天的观看次数，而 b 和 w 是未知参数。

2）定义损失函数：确定一个衡量标准（损失函数），用来评价模型预测的准确性。损失函数的目的是量化预测值与实际值之间的差距。例如，在预测视频点击次数的例子中，损失函数可以是均方误差（MSE），即预测值与实际值之差的平方的平均值。

3）优化模型参数：找到使损失函数最小化的模型参数。这通常是通过优化算法实现的，例如梯度下降法，它逐步调整参数值以减少损失函数的值。

2几种常见的梯度下降小结

批量梯度下降 适合小型数据集，计算准确但效率较低。

随机梯度下降 适合大型数据集，计算效率高但路径不稳定。

小批量梯度下降 是最常见的选择，结合了两者的优势。

带有动量的梯度下降 和 自适应学习率方法 可以进一步提高收敛速度和稳定性，适用于大多数场景。这里不详细展开，更多细节，可见https://www.cnblogs.com/suanfajin/p/18257713

代码运行

运用python 对波士顿房价数据集进行处理

常见回归类型效果的验证，此处运用了sklearn

<code>import numpy as np

import pandas as pd

from sklearn import linear_model

import matplotlib.pyplot as plt

from sklearn.model_selection import train_test_split

#print(sklearn.__version__)

def TrianLinerRegression(X,y):

model = linear_model.LinearRegression()

model.fit(X, y)

print('LinerRegression E(|y-wTx|^2):' + str(np.mean((model.predict(X) - y) ** 2)))

return model

def TrainRidegeRegression(X, y, coeff):

model = linear_model.Ridge(alpha=coeff)

model.fit(X, y)

print('RidegeRegression E(|y-wTx|^2):' + str(np.mean((model.predict(X) - y) ** 2)))

return model

def TrainLassoRegression(X, y ,coeff):

model = linear_model.Lasso(alpha=coeff)

model.fit(X, y)

print('LassoRegression E(|y-wTx|^2):' + str(np.mean((model.predict(X) - y) ** 2)))

return model

def TestModel(X_test, y_test,model):

score = model.score(X_test, y_test)

y_pred = model.predict(X_test)

print('model test score is ' + str(score))

return y_pred, score

回归类型分别为

线性回归(Linear Regression)      

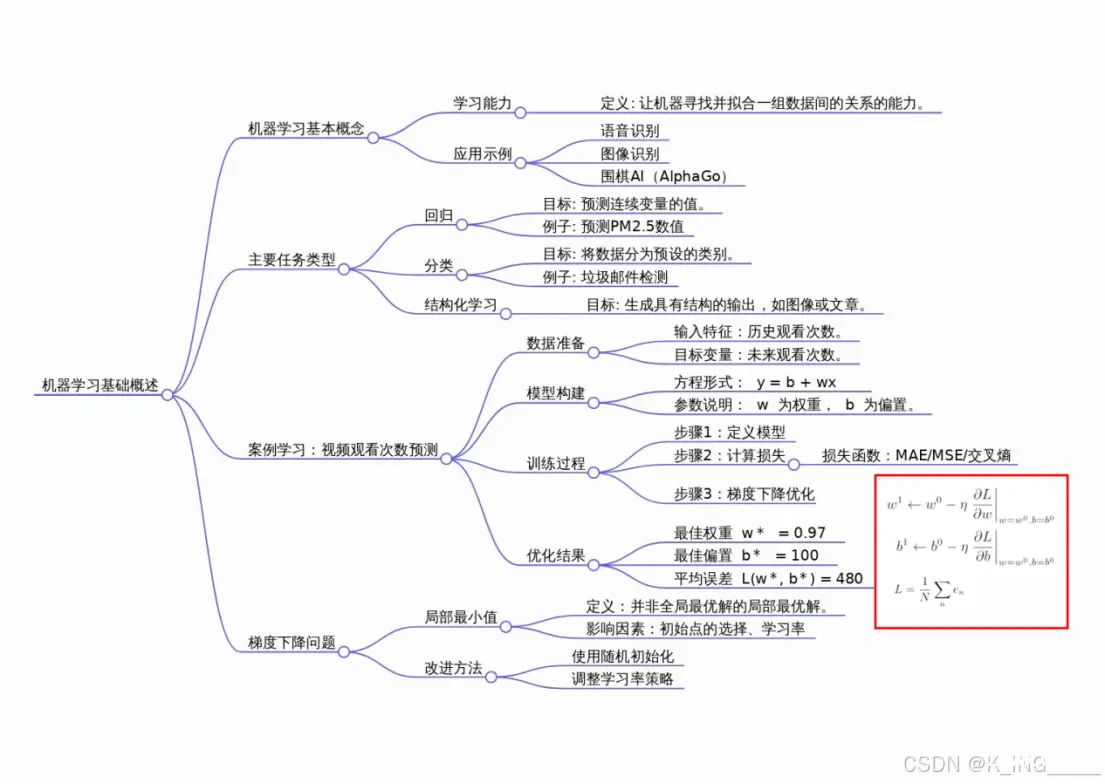
岭回归(Ridge Regression)          

Lassso回归                                  

主函数：

<code>data_url = "http://lib.stat.cmu.edu/datasets/boston"

raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)code>

data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])

label = raw_df.values[1::2, 2]

print('模型数据以及特征 ', data.shape, label.shape)

X_train, X_test, y_train, y_test = train_test_split(data, label, test_size=0.2)

print("训练集 ", X_train.shape, y_train.shape, X_test.shape, y_test.shape)

LinerModel = TrianLinerRegression(X_train, y_train)

RidgeModel = TrainRidegeRegression(X_train, y_train, 0.5)

LassoModel = TrainLassoRegression(X_train, y_train, 0.01)

print()

y_pred_linear, score_linear = TestModel(X_test, y_test, LinerModel)

y_pred_ridge, score_ridge = TestModel(X_test, y_test, RidgeModel)

y_pred_lasso, score_lasso = TestModel(X_test, y_test, LassoModel)

plt.figure()

plt.plot(range(30), y_pred_linear[:30], 'bo-', y_test[:30], 'y.--')

plt.title('Linear model prediction', fontsize='large')code>

plt.figure()

plt.plot(range(30), y_pred_ridge[:30], 'r>-', y_test[:30], 'y.--')

plt.title('Ridge model prediction', fontsize='large')code>

plt.figure()

plt.plot(range(30), y_pred_lasso[:30], 'ks-', y_test[:30], 'y.--')

plt.title('Lasso model prediction', fontsize='large')code>

plt.show()

运行结果：