彻底理解系列之：FP32、FP16、TF32、BF16、混合精度

   

随着大模型的涌现，训练和推理速度成为关键。为提升速度，需减小数据长度以降低存储和带宽消耗。为此，我专注学习并整理了各种精度细节，确保深入理解而非浅尝辄止。

1 从FP32说起

计算机处理数字类型包括整数类型和浮点类型，IEEE 754号标准定义了浮点类型数据的存储结构。一个浮点数由三部分组成：符号位、指数位和尾数位。其中，以最常见的FP32(Float Point 32)为例，其符号位占1位，指数位占8位，尾数位占23位 。

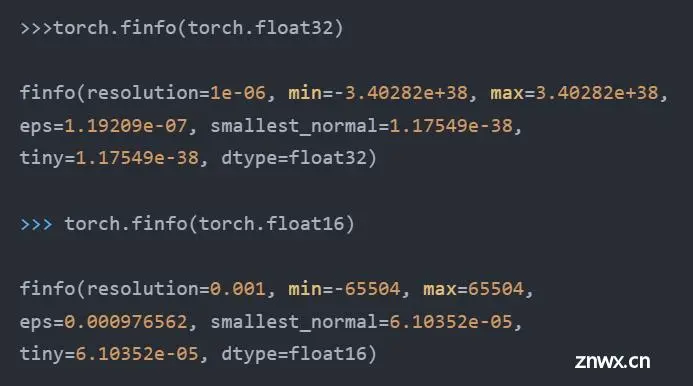
图1. FP32位数分配，来源[2]

Sign：最高位用1位表示符号位，1表示负数，0表示正数，记为SExponent：中间8位表示指数位，记为EMantissa：低位23位表示小数部分，记为M

我们以十进制数9.625为例，看看十进制和FP32二进制之间如何转换：

十进制--》二进制

先分为整数部分9和小数部分0.625。

将9转换为二进制1001,然后通过乘以2并取整数部分的方式得到0.625。接着，将剩余的小数部分0.625再乘以2并取整数部分，如此循环，最终得到0.101。将这两个结果相加，即1001.101,转换为二进制指数形式为1.001101 * 2^3。

根据IEEE 754标准，FP32的指数部分需要加上127以进行偏移，调整为3+127=130。对应的二进制表示为10000010,小数部分补齐至23位后，符号位为0。将这三部分组合起来，便得到了FP32的表示。

0 10000010 00110100000000000000000。

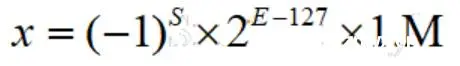
图2. FP32转换工具，来源[3]

二进制--》十进制

将二进制分为S、E、M三部分，将FP32转换为十进制的方法如下：

$S=B_2+B_1+...+B_0$

$E=G_2+G_1+...+G_0$

$M=P_2+P_1+...+P_0$

文章内容经过优化后如下：

"其中，1.M表示小数部分的二进制表示。以S=0,E二进制10000010转为十进制为130为例，M为00110100000000000000000。去掉小数部分后面的无用零后，得到1.M实际上是二进制的1.001101,转换为十进制就是：×"

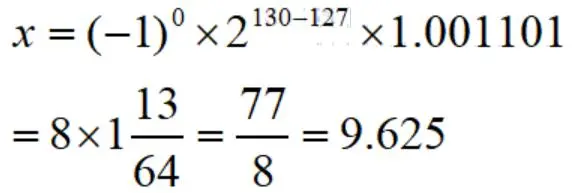
顺利还原回了十进制数。

FP32搞清楚了，FP16、FP64类似，只是指数位和小数位的长度不一样：

2 模型训练中不同精度的问

降低存储负担：提高训练显存利用率至FP32,实现一半存储占用，从而在有限的GPU资源下训练更大模型或提高batch_size。

FP16和FP32都是深度学习中常用的数值表示方式。FP16是16位浮点数表示法，即半精度浮点数，用一个16位的数值来表示实数，包括1位符号位、5位指数位和10位尾数位。FP16的精度比FP32低，但计算速度快，内存占用小，因此在深度学习中常用于加速训练和推理。FP32是32位浮点数表示法，即单精度浮点数，用一个32位的数值来表示实数，包括1位符号位、8位指数位和23位尾数位。FP32是深度学习中最常用的数值表示方式之一，因为它提供了足够的精度和计算速度，同时也相对容易实现。

但是，是否意味着我们都使用FP16就行了呢？当然不是。主要原因是位数少同时有两个劣势：(1)精度较低；(2)存储空间较大。

位数少时精度比位数多时低，可能导致准确度不够；位数少时表示的范围比位数多时要小，可能导致数据溢出，装不下了。

先看看精度问题，以下是用FP64、FP32、FP16表示1/3时不同的精度：

提高精度，确保数据表示和计算的准确性，使模型训练拟合出的参数更精确。这取决于我们对模型精度的具体要求。

我们用一个大数10^6看看二者能否表示：

3混合精度

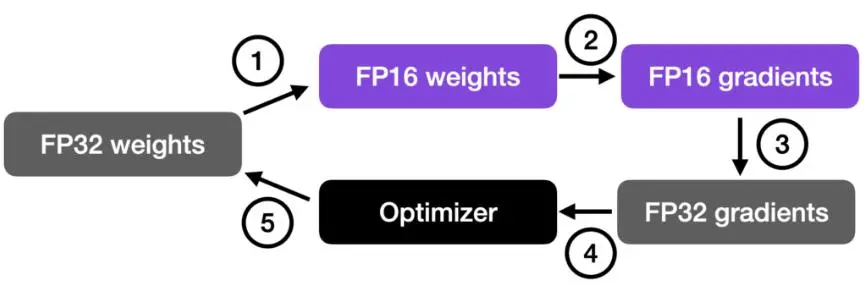
图3. 混合精度使用流程，来源[1]

把神经网络权重参数由初始化的FP32转为FP16；用FP16进行前向和后向计算，并进行梯度计算；把FP16的梯度转为FP32；使用FP32的梯度和学习率learning rate相乘；使用FP32更新网络权重，得到FP32的更新后的权重。

使用FP32更新权重的时候，梯度乘上学习率后一般数值都比较小，因此使用FP32能防止精度不够。

在混合精度训练中，采用"损失缩放"技术以防止数值过小导致精度损失。首先，将损失扩大一倍，使其位于FP16可表示范围内；然后进行反向计算；最后，将梯度缩小相同的倍数，以确保最终数值的准确性。

DistilBERT模型在电影情感分类任务上进行了微调，通过比较FP32、FP16和混合使用性能及准确率，展示了其优越性。

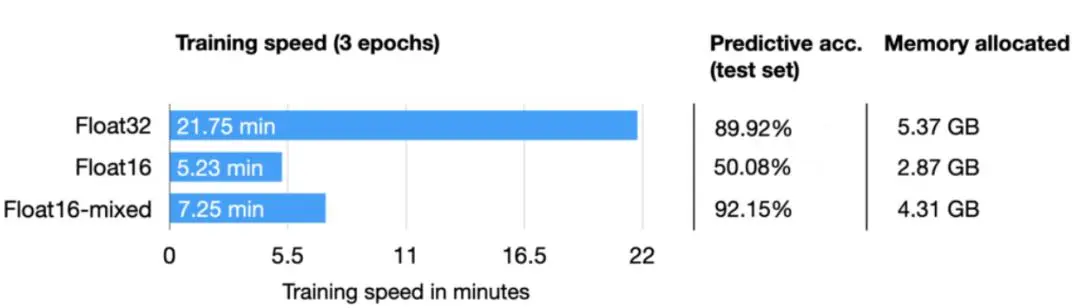
图4. FP32、FP16和混合精度训练对比，来源[1]

如图4所示，混合精度训练时间与FP16相当，约为FP32的1/3,且使用的存储空间介于二者之间。尽管预测准确率与FP32相近，甚至更高，但作者认为这可能是因为正则化的影响。相较之下，FP16的预测准确率较低，可能是由于训练过程中数据溢出导致模型失准。

4BF16、TF32

FP16的指数和尾数限制了其可表示的数据范围，因此谷歌为深度学习引入了BF16格式。BF16与FP16共享相同的16位总长度，但将指数位从5位扩展至8位，小数位数则缩短至7位，从而扩大了整数表示范围。

英伟达为满足GPU需求，推出了TF32数据类型，具有8位指数、10位小数(与FP16相同),相较于BF16多出3位小数。

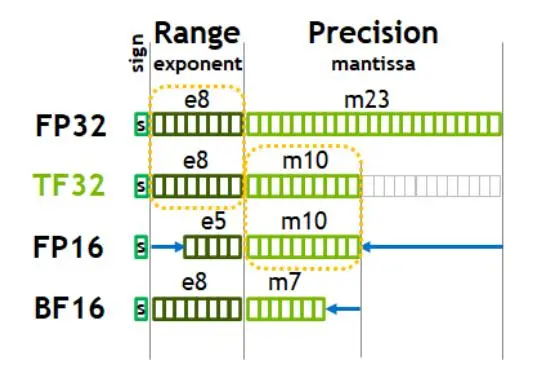
图5. BF16、TF32位数，来源：英伟达白皮书

图6. 各种精度综合对比

BF16是一种高效的数据格式，具有较短的计算时间(与FP16相当)和较少的存储需求(小数位数较少)。同时，它在准确性方面表现出色，达到了92%,与其他同类格式相当。这些优势使得BF16成为一种值得关注的技术选择。

到此结束，我们搞清楚了各种浮点类型的定义、转换、模型训练时如何使用，以及性能对比。

-对此，您有什么看法见解？-

-欢迎在评论区留言探讨和分享。-