【AI论文解读】【AI知识点】【AI小项目】【AI战略思考】

NP 难问题（NP-Hard Problem） 是计算复杂性理论中的一个重要概念，描述了那些非常难以求解的问题。NP 难问题中的“NP”代表“非确定性多项式时间”（Nondeterministic Polynomial time）。这些问题的特性使得求解它们的最佳算法目前尚未找到，甚至可能不存在通用的快速求解方法。

1. NP 难问题的背景

为了理解 NP 难问题，首先需要了解几个关键概念：P类问题、NP类问题、NP完全问题 和 NP 难问题。它们是计算复杂性理论中研究问题难度的不同分类。

a. P类问题

P类问题（Polynomial time problems）是指那些能够在多项式时间内通过确定性算法求解的问题。换句话说，对于 P类问题，我们已经有高效的算法，能够在合理的时间范围内解决这些问题。

例子：对一个给定的数列进行排序是一个P类问题，因为我们可以使用像快速排序、归并排序等算法，在多项式时间内（如

O

(

n

log

⁡

n

)

O(n \log n)

O(nlogn)）完成排序。

b. NP类问题

NP类问题（Nondeterministic Polynomial time problems）是那些可以在多项式时间内验证解是否正确的问题。注意，NP类问题不一定能在多项式时间内求解，但如果给出一个候选解，可以快速验证它是否为正确解。

例子：例如旅行商问题（Traveling Salesman Problem, TSP），给定一条路径，虽然找到这条路径可能很难，但验证这条路径是否是最短路径可以在多项式时间内完成。因此，TSP属于NP类问题。

c. NP完全问题

NP完全问题（NP-Complete problems）是NP类问题中的一种特殊子集。这些问题不仅属于NP类问题（即解可以在多项式时间内验证），并且所有的NP类问题都可以通过某种方式归约为这些问题。换句话说，NP完全问题是最难的NP问题，它们之间存在某种等价性。如果你能够找到一种快速解决NP完全问题的方法，那么所有的NP类问题都可以在多项式时间内求解。

例子：旅行商问题（TSP）、布尔可满足性问题（SAT）和顶点覆盖问题（Vertex Cover）都是NP完全问题。

d. NP 难问题

NP 难问题（NP-Hard problems）是指那些至少和NP完全问题一样难的问题。NP 难问题不要求解必须属于NP类问题，它们可以比NP类问题更难，甚至可能无法验证解是否正确。换句话说，NP 难问题包含了NP完全问题，但还包括那些不属于NP类的、更为广泛的问题。

关键点：如果你能在多项式时间内解决一个NP 难问题，那么你就能够在多项式时间内解决所有NP完全问题。因此，NP 难问题的解决方案对于整个复杂性理论是至关重要的。

例子：旅行商问题的一个变种——寻找所有城市的最短路径问题（不限起点和终点），就是一个NP 难问题。另一个例子是经典的哈密顿路径问题（Hamiltonian Path Problem），即在一个图中找到一个经过每个顶点一次的路径，这也是NP 难问题。

2. P类、NP类与NP 难问题的关系

理解这些问题的相互关系，可以通过一个简化的图来表示：

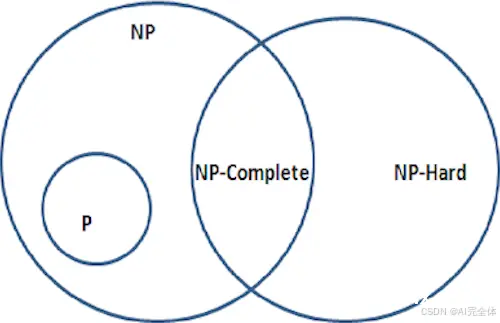
图片来源：https://medium.com/@p.yun1994/p-np-np-hard-and-np-complete-problems-fe679bd1cf9c

P类问题：可以在多项式时间内求解。NP类问题：解可以在多项式时间内验证，但求解不一定是多项式时间。NP完全问题：既属于NP类问题，也属于NP 难问题。NP 难问题：至少和NP完全问题一样难，但不一定是NP类问题（即解不一定能在多项式时间内验证）。

3. NP 难问题的特点

a. 无法快速求解

NP 难问题的主要特点是我们目前没有已知的算法能够在多项式时间内求解这些问题。换句话说，随着问题规模的增加，解决NP 难问题的计算复杂度会迅速增长，通常是指数级的。

b. 归约性

NP 难问题具有归约性：如果某个问题是NP 难的，那么其他NP类问题可以归约为这个问题。这意味着解决了一个NP 难问题，就可以通过类似的方法解决其他NP 难问题。

c. 计算复杂性极高

在大多数实际应用中，直接求解NP 难问题是不现实的，因为所需的计算资源随着输入规模的增长而呈指数级增长。例如，在旅行商问题中，随着城市数量的增加，计算所有可能路径的时间将迅速超过任何实际可行的计算能力。

4. NP 难问题的实际例子

a. 旅行商问题（Traveling Salesman Problem, TSP）

给定一组城市，要求找到一条经过每个城市一次的最短路径。该问题的求解是NP 难的，因为随着城市数量的增加，可能的路径数呈指数增长。

b. 背包问题（Knapsack Problem）

给定一组物品，每个物品都有一个重量和价值，在总重量不超过背包容量的前提下，选择物品以使总价值最大化。这个问题也是NP 难问题，特别是当物品数量较多时，计算所有可能的组合非常耗时。

c. 布尔可满足性问题（SAT）

布尔可满足性问题是指给定一组布尔表达式，确定是否存在一个变量赋值，使得整个表达式为真。SAT问题是NP完全问题，也是NP 难问题。

d. 图着色问题（Graph Coloring Problem）

在图着色问题中，要求使用最少的颜色对图中的节点进行着色，使得相邻节点之间的颜色不同。这个问题也是NP 难问题，随着图的规模增大，找到最优解的难度迅速增加。

5. 解决NP 难问题的方法

由于NP 难问题无法在多项式时间内有效求解，通常需要借助一些启发式算法或近似算法来找到近似解。这些方法在大多数情况下能够快速找到“足够好”的解，而不追求最优解。

a. 启发式算法

启发式算法（Heuristic Algorithms）通过使用经验规则或简化问题来快速找到近似解。虽然它们不保证找到最优解，但能够显著降低求解时间。例如，贪心算法、爬山算法、模拟退火算法等都是常见的启发式算法。

b. 近似算法

近似算法通过在合理的时间内生成接近最优解的方案。对于某些NP 难问题，可以设计一个近似度界限，例如在旅行商问题中，找到一个不超过最优解一定倍数的近似解。

c. 分支定界法（Branch and Bound）

分支定界法通过系统地探索问题的解空间，并在解空间中剪枝，排除一些明显不可能产生最优解的解，从而减少计算量。

d. 动态规划

在某些特殊情况下，动态规划可以用来求解NP 难问题的特定子集。虽然动态规划不适合所有NP 难问题，但对于某些具有递归性质的问题（如背包问题的某些变体），它是一个有效的方法。

6. 总结

NP 难问题（NP-Hard Problems） 是计算复杂性理论中一些最难的问题类别，它们至少和NP完全问题一样难，甚至可能更难。NP 难问题的求解通常无法在多项式时间内完成，随着问题规模的增加，求解时间呈指数级增长。尽管精确求解这些问题非常困难，但通过启发式方法、近似算法和动态规划等技术，能够在合理的时间内找到近似解。这些方法在实际应用中广泛使用，用于解决大规模优化问题、资源分配问题等。