【数据结构】二叉搜索树(Java + 链表实现)
明志学编程- 2024-08-14 11:05:02 阅读 93
Hi~!这里是奋斗的明志,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~
🌱🌱个人主页:奋斗的明志
🌱🌱所属专栏:数据结构、LeetCode专栏

📚本系列文章为个人学习笔记,在这里撰写成文一为巩固知识,二为展示我的学习过程及理解。文笔、排版拙劣,望见谅。

这里写目录标题
前言一、二叉搜索树1.概念2.search 搜索或查找3.insert 插入4.删除(难点)4.1 根结点的左子树为空4.2 根结点的右子树为空4.3 根结点的左右子树都不为空4.4 完整代码
5.性能分析
二、1.7 和 java 类集的关系三、搜索1.概念及场景2.模型
前言
Map接口是独立的
实现Iterable接口的集合都是可以使用 for - Each 语句进行打印的
搜索性能会非常高
一、二叉搜索树
1.概念
二叉搜索树又称为二叉排序树,它或者是一棵空树,或者是具以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
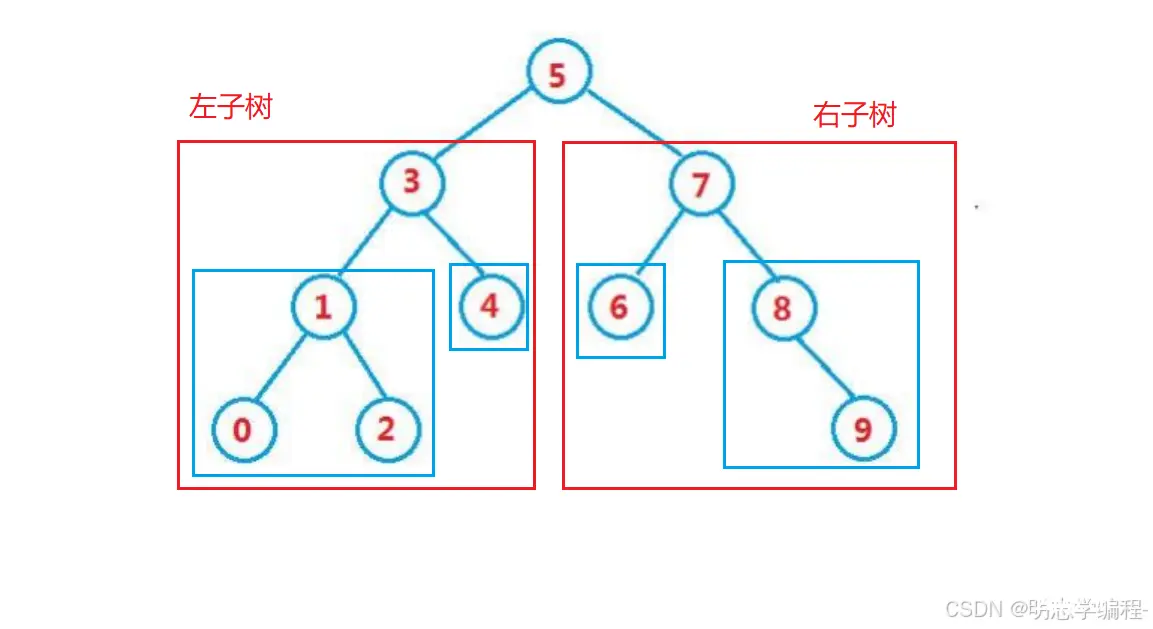
<code>如果中序遍历这棵二叉搜索树,会发现遍历的结果是有序的
接下来就模拟实现一下二叉搜索树
首先,和之前二叉树的实现一样,都是一个节点包括值和指向左右节点的引用(利用孩子兄弟表示法)
public class BinarySearchTree { -- -->
//首先这棵树是由若干个结点组成的
static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
//提供构造方法进行初始化
public TreeNode(int val) {
this.val = val;
}
}
//根节点
public TreeNode root;
}
2.search 搜索或查找
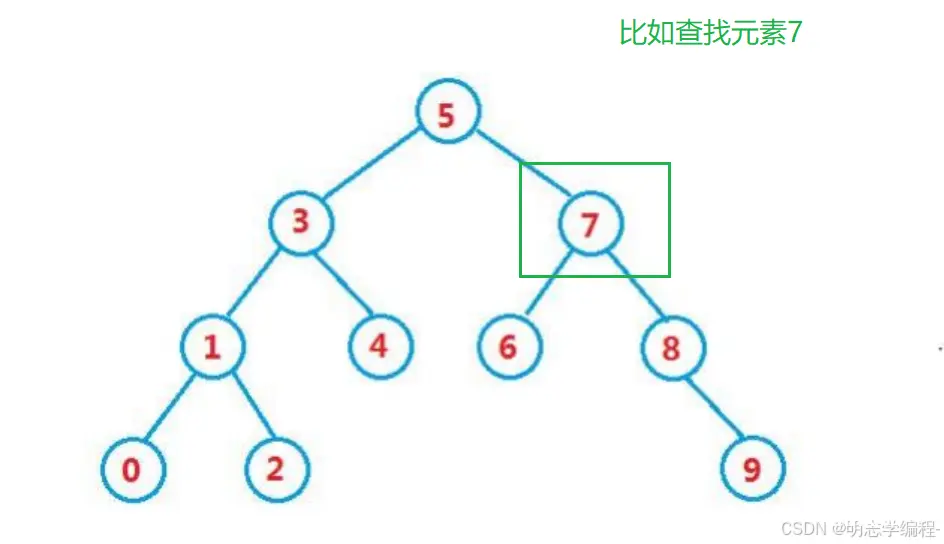
若根节点不为空:
如果 查找key == 根节点的值 返回true
如果 查找key > 根节点的值 在其右子树查找
如果 查找key < 根节点的值 在其左子树查找
<code>/**
* search 搜索的意思
*
* @param val
* @return
*/
public boolean search(int val) { -- -->
TreeNode cur = root;
while (cur != null) {
if (val > cur.val) {
cur = cur.right;
} else if (val < cur.val) {
cur = cur.right;
} else {
return true;
}
}
return false;
}
算法从根节点开始,根据当前节点的值与 val 的大小关系,决定是向左子树还是向右子树移动,直到找到匹配的节点或者搜索到空节点为止。因为每一步都是根据节点值的大小进行移动,而树的高度(树的深度)是 log(n) 级别的(其中 n 是树中节点的数量),所以在平均情况下,search 方法的时间复杂度是 O(log n)。
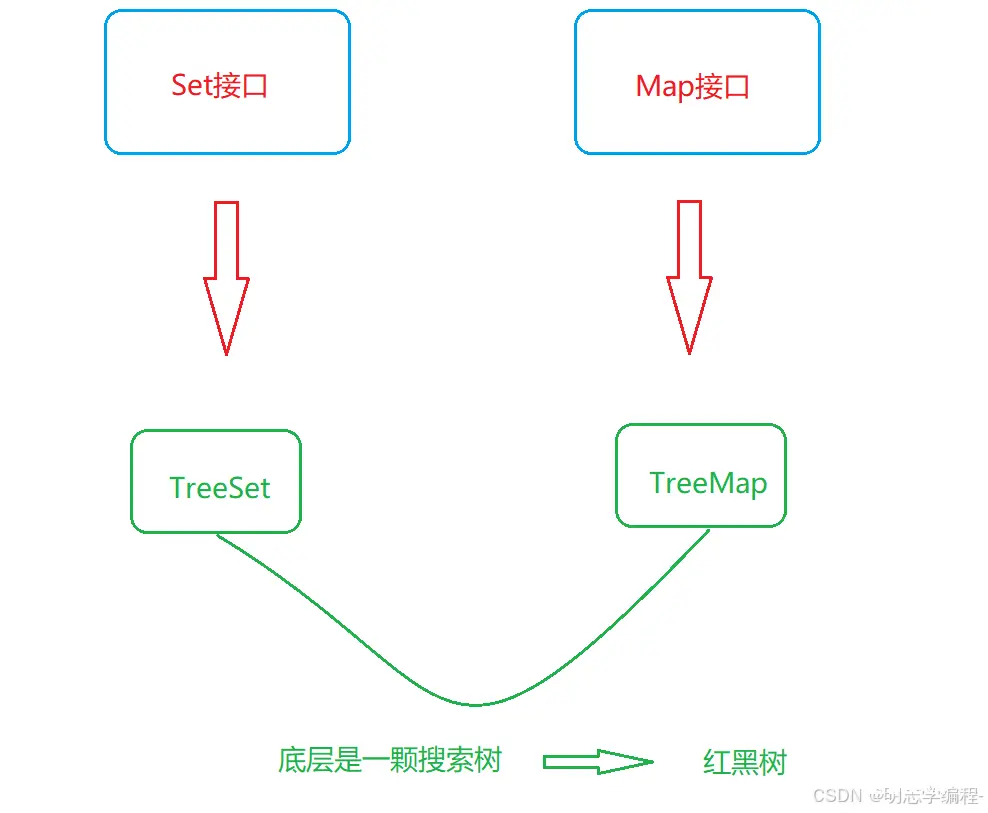
3.insert 插入
如果该树为空树,即 根节点 == null 直接实例化一个结点,进行插入
如果树不是空树,按照查找逻辑确定插入位置,插入新的节点
<code>public void insert(int val) { -- -->
//判断是否是空树
if (root == null) {
root = new TreeNode(val);
return;
}
//定义一个前驱结点
TreeNode parent = null;
//定义一个临时节点
TreeNode cur = root;
while (cur != null) {
if (val > cur.val) {
parent = cur;
cur = cur.right;
} else if (val < cur.val) {
parent = cur;
cur = cur.left;
} else {
return;
}
}
//插入的这个结点
TreeNode node = new TreeNode(val);
if (val > parent.val) {
parent.right = node;
}
if (val < parent.val) {
parent.left = node;
}
}
这个方法用于向二叉搜索树中插入一个新的节点,如果节点已经存在则不插入。插入操作首先需要找到要插入位置的父节点,然后根据 val 的大小决定是插入为左子节点还是右子节点。与 search 方法类似,插入操作的时间复杂度也取决于树的高度。在平均情况下,插入一个节点的时间复杂度也是 O(log n)。
4.删除(难点)
设待删除结点为cur,待删除节点的双亲结点为parent
4.1 根结点的左子树为空
cur.left == null
cur 是 root,则 root == cur.right
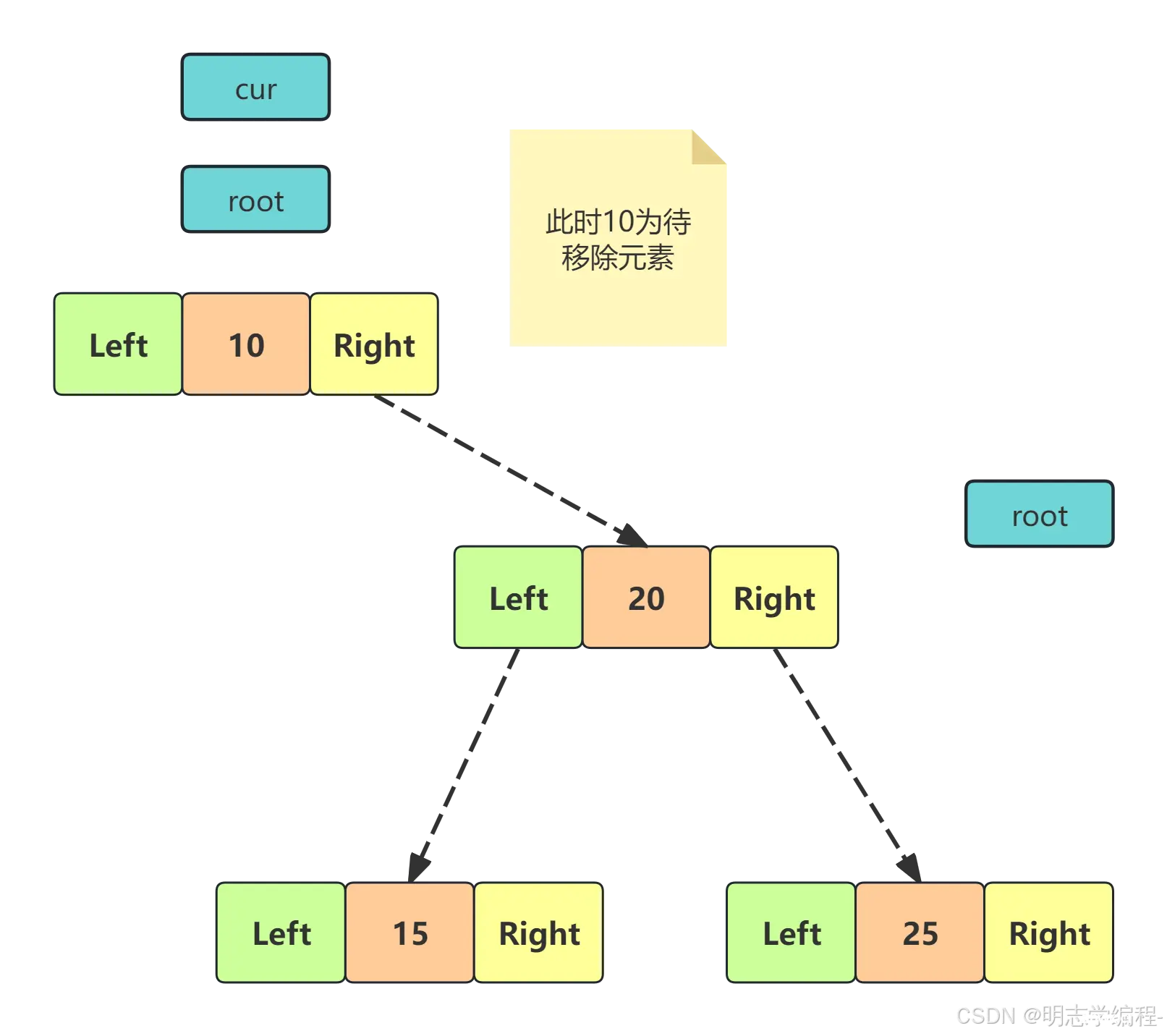
<code>cur 不是 root ,cur 是 parent.left,则 parent.left = cur.right
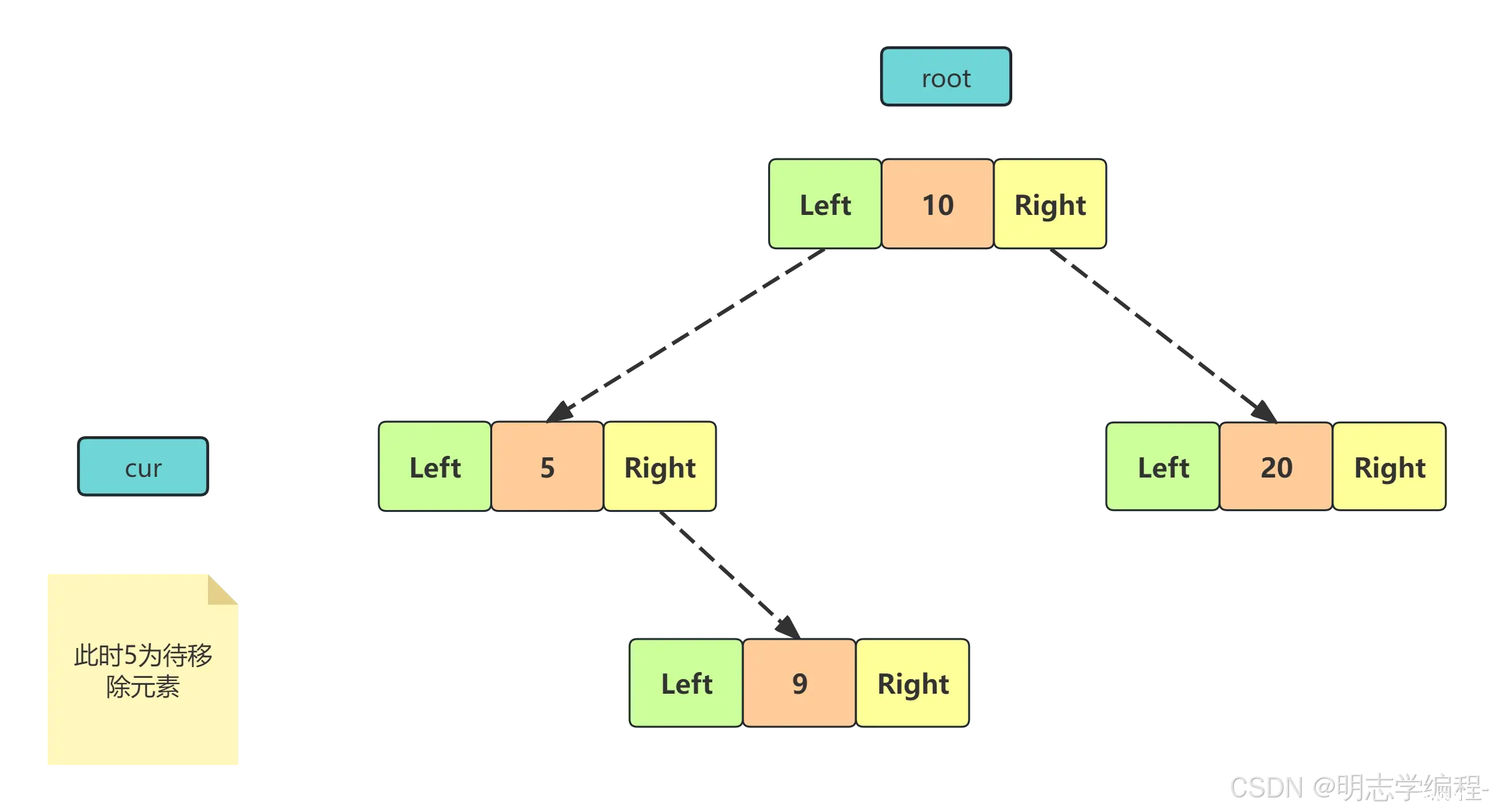
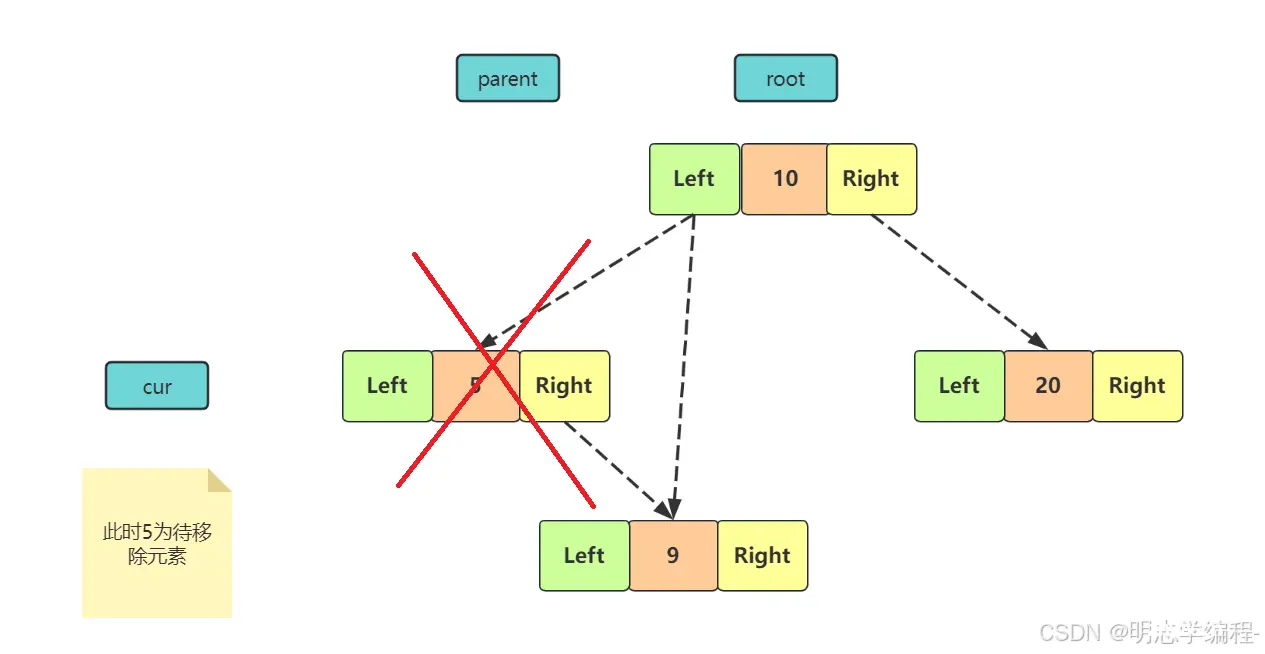
<code>cur 不是 root ,cur 是 parent.right,则 parent.right = cur.right
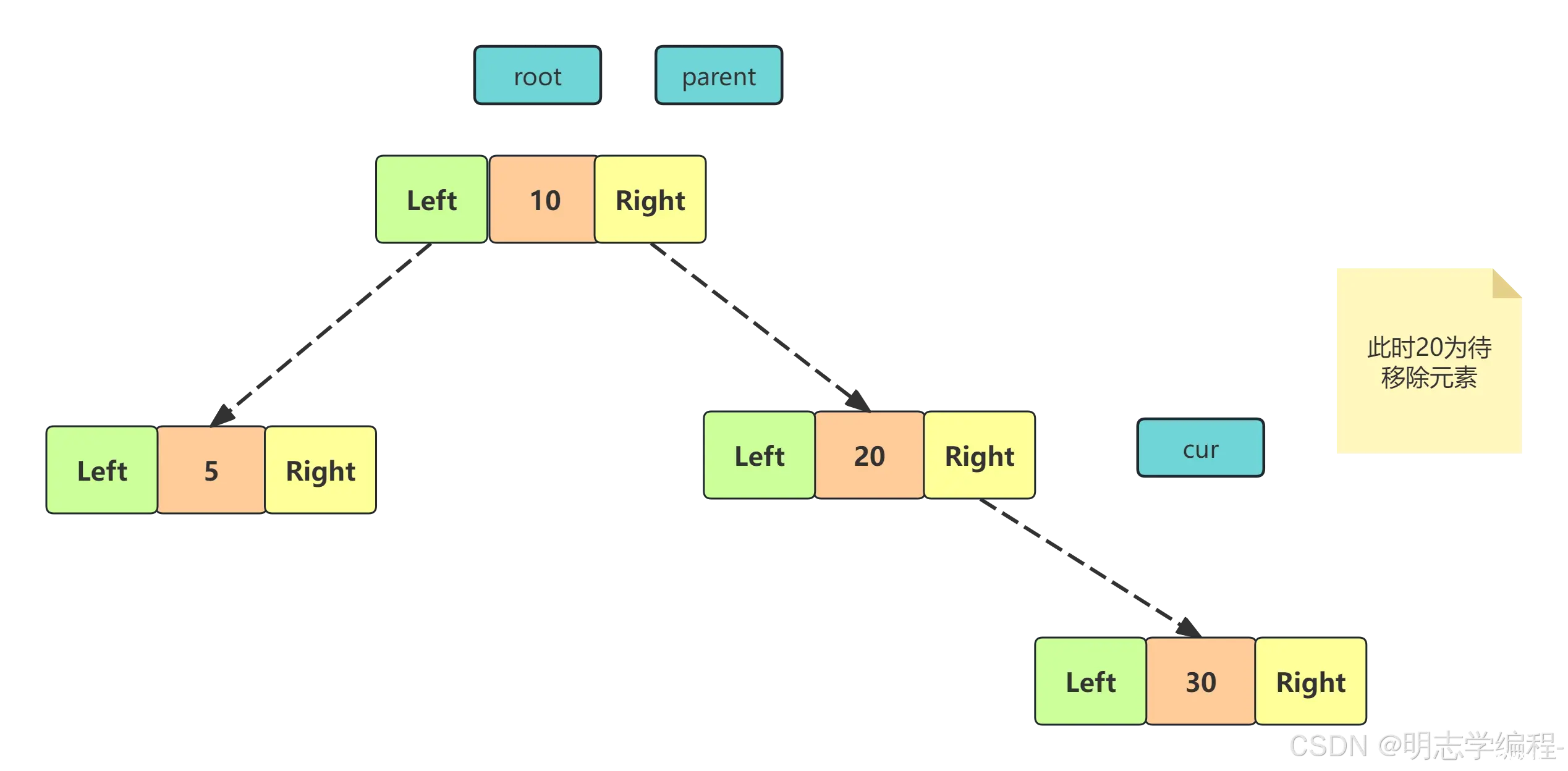
4.2 根结点的右子树为空
<code>cur.right == null
cur 是 root,则 root = cur.left

<code>cur 不是 root ,cur 是 parent.left,则 parent.left = cur.left
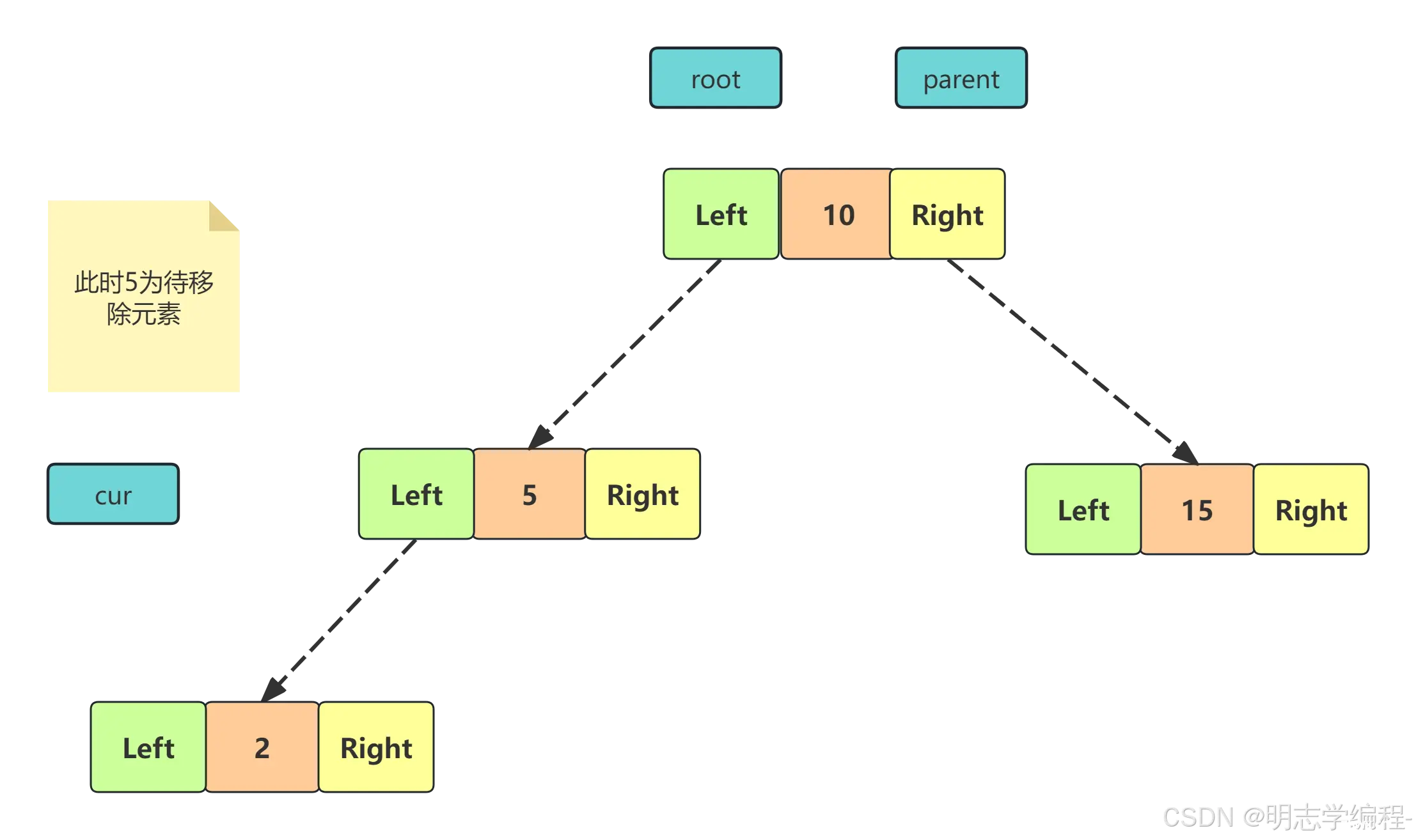
<code>cur 不是 root ,cur 是 parent.right,则 parent.right = cur.left
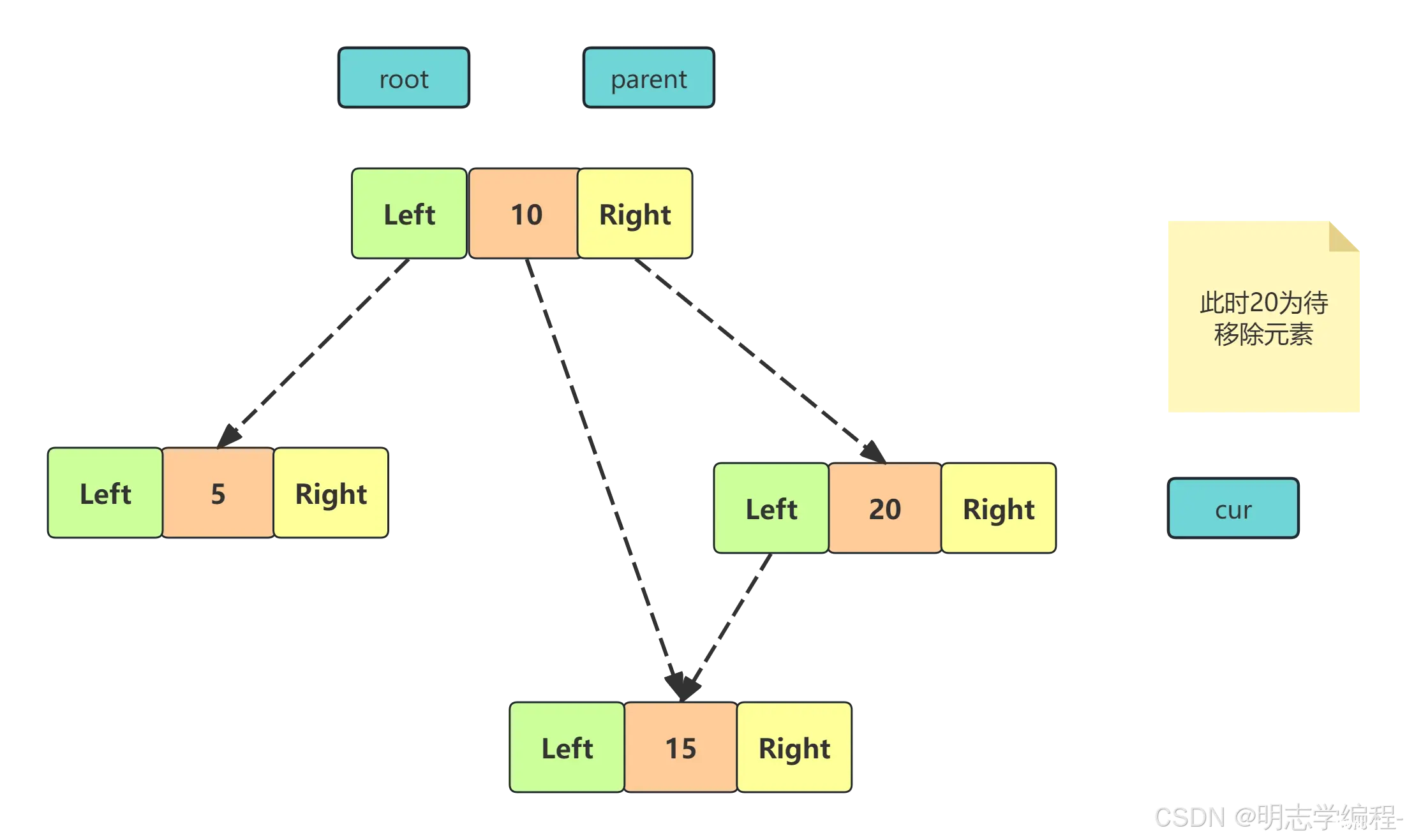
4.3 根结点的左右子树都不为空
<code>cur.left != null && cur.right != null
需要使用替换法进行删除,即在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被 删除节点中,再来处理该结点的删除问题
删除结点的左树的最大值,替换当前删除的结点(一定没有左子树)删除结点的右树的最小值,替换当前删除的结点(一定没有右子树)
【情况一】
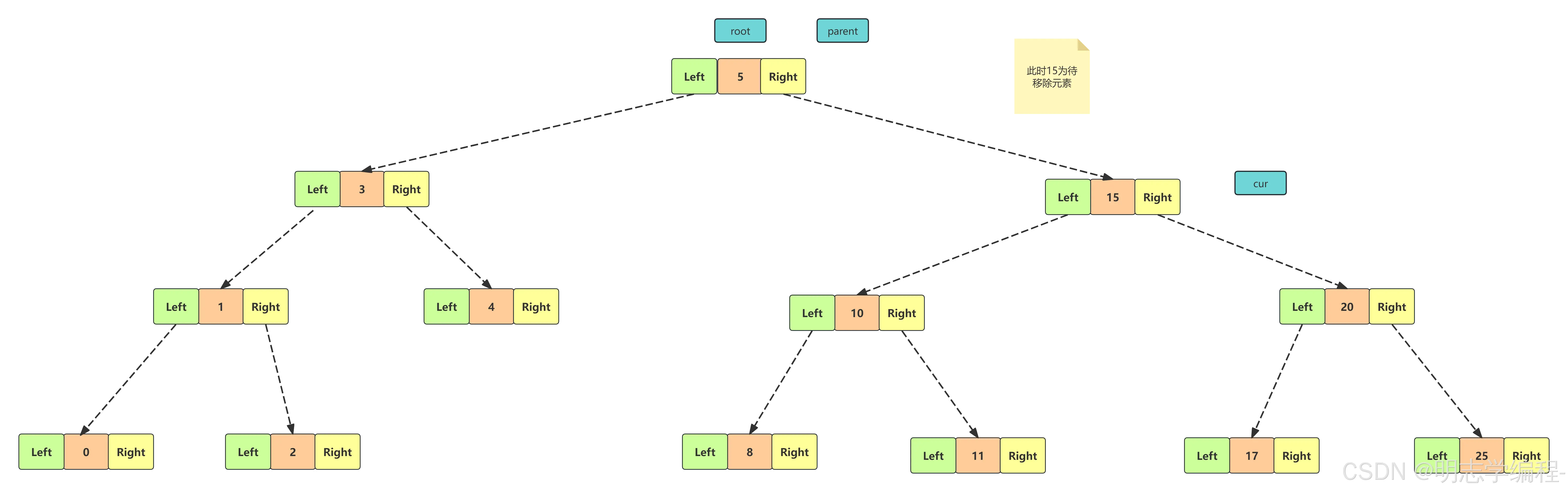
【情况二】
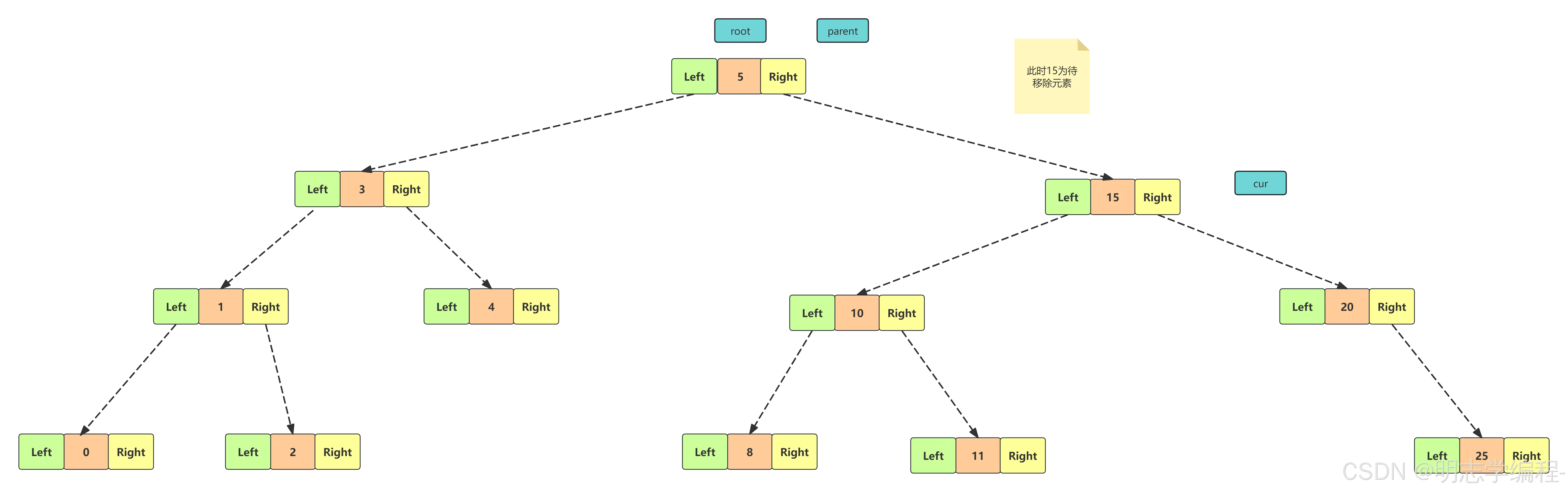
4.4 完整代码
<code>/**
* 删除这个结点
* 利用替换的思路
*
* @param val
*/
public void remove(int val) { -- -->
//首先需要查找该树有没有该值
TreeNode cur = root;
TreeNode parent = null;
while (cur != null) {
if (val > cur.val) {
parent = cur;
cur = cur.right;
} else if (val < cur.val) {
parent = cur;
cur = cur.left;
} else {
//如果等于的话,说明该树有该值
removeNode(parent, cur);
return;
}
}
}
//进行覆盖的方法,删除结点
private void removeNode(TreeNode parent, TreeNode cur) {
if (cur.left == null) {
if (cur == root) {
root = cur.right;
} else if (cur == parent.left) {
parent.left = cur.right;
} else {
parent.right = cur.right;
}
} else if (cur.right == null) {
if (cur == root) {
root = cur.left;
} else if (cur == parent.left) {
parent.left = cur.left;
} else {
parent.right = cur.left;
}
} else {
TreeNode t = cur.right;
TreeNode tp = cur;
while (t.left != null) {
tp = t;
t = t.left;
}
cur.val = t.val;
if (tp.left == t) {
tp.left = t.right;
} else {
tp.right = t.right;
}
}
}
5.性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度 的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
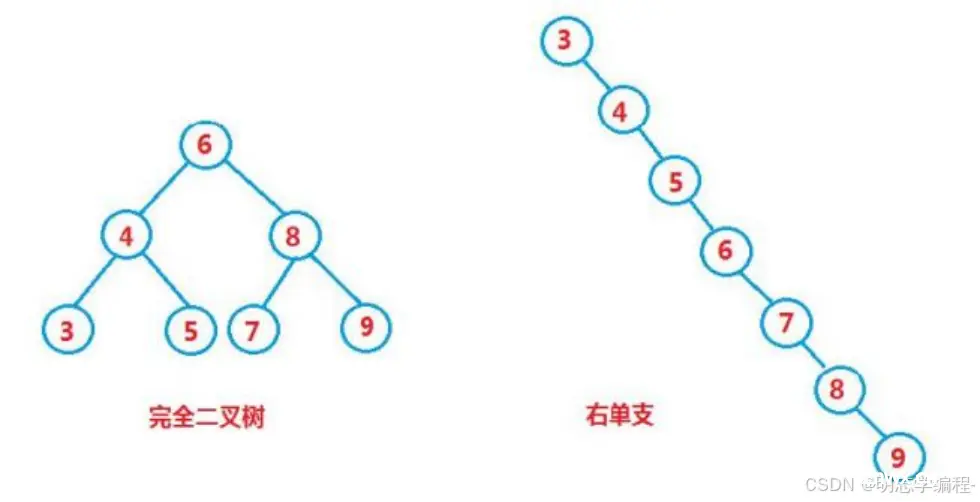
最优情况下,二叉搜索树为完全二叉树,其平均比较次数为: log2N 最差情况下,二叉搜索树退化为单支树,其平均比较次数为:

问题:如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插入关键码,都可以 是二叉搜索树的性能最佳?
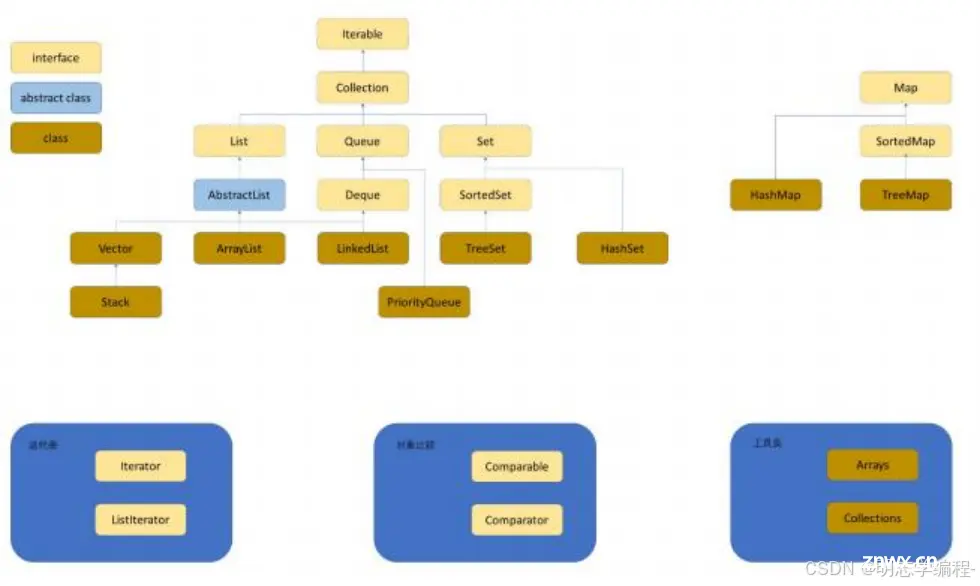
二、1.7 和 java 类集的关系
<code>TreeMap 和 TreeSet 即 java 中利用搜索树实现的 Map 和 Set;实际上用的是红黑树,而红黑树是一棵近似平衡的 二叉搜索树,即在二叉搜索树的基础之上 + 颜色以及红黑树性质验证,关于红黑树的内容后序再进行介绍
三、搜索
1.概念及场景
Map和set是一种专门用来进行搜索的容器或者数据结构,其搜索的效率与其具体的实例化子类有关。以前常见的 搜索方式有:
直接遍历,时间复杂度为O(N),元素如果比较多效率会非常慢二分查找,时间复杂度为o(log N) ,但搜索前必须要求序列是有序的
上述排序比较适合静态类型的查找,即一般不会对区间进行插入和删除操作了,而现实中的查找比如:
根据姓名查询考试成绩通讯录,即根据姓名查询联系方式不重复集合,即需要先搜索关键字是否已经在集合中
可能在查找时进行一些插入和删除的操作,即动态查找,那上述两种方式就不太适合了,本节介绍的Map和Set是 一种适合动态查找的集合容器。
2.模型
一般把搜索的数据称为关键字(Key),和关键字对应的称为值(Value),将其称之为Key-value的键值对,所以 模型会有两种:
纯 key 模型,比如:
有一个英文词典,快速查找一个单词是否在词典中 。快速查找某个名字在不在通讯录中
Key-Value 模型,比如:
统计文件中每个单词出现的次数,统计结果是每个单词都有与其对应的次数: <单词,单词出现的次数> 。梁山好汉的江湖绰号:每个好汉都有自己的江湖绰号
而Map中存储的就是key-value的键值对, Set中只存储了Key。


声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。