1.用栈实现队列

. - 力扣（LeetCode）

思路

1.将一个栈当作输入栈，用于压入 push 传入的数据；另一个栈当作输出栈，用于 pop 和 peek 操作。

2.每次 pop 或 peek 时，若输出栈为空则将输入栈的全部数据依次弹出并压入输出栈，这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序。

<code>class MyQueue {

private:

stack<int> inStack, outStack;

void in2out() {

while (!inStack.empty()) {

outStack.push(inStack.top());

inStack.pop();

}

}

public:

MyQueue() {}

void push(int x) {

inStack.push(x);

}

int pop() {

if (outStack.empty()) {

in2out();

}

int x = outStack.top();

outStack.pop();

return x;

}

int peek() {

if (outStack.empty()) {

in2out();

}

return outStack.top();

}

bool empty() {

return inStack.empty() && outStack.empty();

}

};

2. 用队列实现栈

<code>class MyStack {

public:

queue<int> queue1;

queue<int> queue2;

/** Initialize your data structure here. */

MyStack() {

}

/** Push element x onto stack. */

void push(int x) {

queue2.push(x);

while (!queue1.empty()) {

queue2.push(queue1.front());

queue1.pop();

}

swap(queue1, queue2);

}

/** Removes the element on top of the stack and returns that element. */

int pop() {

int r = queue1.front();

queue1.pop();

return r;

}

/** Get the top element. */

int top() {

int r = queue1.front();

return r;

}

/** Returns whether the stack is empty. */

bool empty() {

return queue1.empty();

}

};

3.数组中的第k个最大元素 

 思路：

1.先取数组的前k个元素，使用向上调整算法建立小堆（a[0]为最小值）

2.再遍历剩余数组，如果元素大于a[0],则替代a[0]入堆并使用向下调整算法调整

3.返回a[0]；

<code>

typedef struct heap

{

int* a;

int size;

int capacity;

}HP;

void swap(int* p1, int* p2)

{

int t = 0;

t = *p1;

*p1 = *p2;

*p2 = t;

}

void heapinit(HP* php)

{

assert(php);

php->a = NULL;

php->size = 0;

php->capacity = 0;

}

void adjustup(int* a, int child) //向上调整法 //上方必须是堆

{

int parent = (child-1)/2;

while (child>0)

{

if (a[parent]>=a[child]) //小堆为>=,大堆为<=

{

swap(&a[parent],&a[child]);

child = parent;

parent = (child - 1)/2;

}

else

{

break;

}

}

}

void adjustdown(int* a,int n, int parent) //向下调整法，！！！！！！（仅适用于根结点两端都是大堆或小堆）

{

int child = 2 * parent + 1;

while (child<=n) //

{

if (child + 1<=n && a[child + 1] < a[child]) // child+1>n可以推出child==n，所以只有左孩子

{

child++; //选出左右孩子中最大的一个‘>’,最小的为'<'

}

if (a[parent]>=a[child]) //大堆为“<=”,小堆为“>=”

{

swap(&a[parent], &a[child]);

parent = child;

child = 2 * parent + 1; //每次都先找左孩子

}

else

{

break;

}

}

}

void heappush(HP* php, int data)

{

php->a[php->size] = data;

php->size++;

adjustup(php->a, php->size - 1);

}

int findKthLargest(int* nums, int numsSize, int k) {

HP sl;

heapinit(&sl);

sl.a=(int*)malloc(sizeof(int)*k);

int i=0;

for(i=0;i<k;i++)

heappush(&sl, nums[i]);

for(i=k;i<numsSize;i++)

{

if(nums[i]>sl.a[0])

{

sl.a[0]=nums[i];

adjustdown(sl.a,k-1,0); //记得是k-1

}

}

return sl.a[0];

}

4.最小栈 

<code>class MinStack {

public:

public:

    void push(int x) {

   

    // 只要是压栈，先将元素保存到_elem中

    _elem.push(x);

   

    // 如果x小于_min中栈顶的元素，将x再压入_min中！！！！！！！！！！

    if (_min.empty() || x <= _min.top())

        _min.push(x);

}

void pop() {

// 如果_min栈顶的元素等于出栈的元素，_min顶的元素要移除！！！！！！！！

    if (_min.top() == _elem.top())

        _min.pop();

   

    _elem.pop();

}

int top()

{

return _elem.top();

}

int getMin()

{

return _min.top();

}

private:

// 保存栈中的元素

std::stack<int> _elem;

// 保存栈的最小值

std::stack<int> _min;

};

5.栈的弹出压入序列 

1.设置flag，i，i用来遍历pushv数组；

2.当arr.top()==popV[flag]时，arr.pop(),flag++,

3.当pushV[i]==popV[flag]时，flag++；

4.遍历完成后，

for(;flag<popV.size();flag++)

          {

            if(popV[flag]!=arr.top())

            return false;

            else

             {

                arr.pop();

             }

          }

5.return true

<code>class Solution {

public:

bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {

int flag=0;

for(int i=0;i<pushV.size();i++)

{

if(pushV[i]!=popV[flag])

{

if(!arr.empty())

{

if(arr.top()==popV[flag])

{

arr.pop();

flag++;

while(!(arr.empty())&&arr.top()==popV[flag])

//如果连续遇到arr.top()==popV[flag]，则一直arr.pop();flag++，直至两者不同

{

arr.pop();

flag++;

}

arr.push(pushV[i]);

}

else {

arr.push(pushV[i]);

}

}

else

arr.push(pushV[i]);

}

else

{

flag++;

}

}

for(;flag<popV.size();flag++)

{

if(popV[flag]!=arr.top())

return false;

else

{

arr.pop();

}

}

return true;

}

private:

stack<int> arr;

};

6.逆波兰表达式求值 

1.设置两个stack，一个存数字（arr），一个存符号（brr）

2.遍历数组，若为数字则 入栈arr；

3.若为符号，则入栈brr，并取brr.top,arr.top(两次)

进行operation，并把返回值压入arr栈中；

4.返回arr.top;

<code>class Solution {

public:

int operation(int a, int b, string s) {

if (s[0] == '+')

return b + a; //记得是b在前，a在后，因为栈是后进先出

if (s[0] == '-')

return b - a;

if (s[0] == '*')

return b * a;

if (s[0] == '/')

return b / a;

return 1; // 记得写一个return

// 1，因为系统判定如果if都不走，那么就没有返回值

}

int evalRPN(vector<string>& tokens) {

int num = 0;

int result = 0;

string j;

int a;

int b;

int end;

for (int i = 0; i < tokens.size(); i++) {

if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" ||

tokens[i] == "/") {

brr.push(tokens[i]);

a = arr.top();

arr.pop();

b = arr.top();

arr.pop();

end = operation(a, b, brr.top());

arr.push(end);

brr.pop();

} else {

j = tokens[i];

if (j[0] == '-') {

for (int i = 1; i < j.size(); i++) {

num = num * 10 + (j[i] - '0');

}

arr.push(-num);

num = 0;

} else {

for (int i = 0; i < j.size(); i++) {

num = num * 10 + (j[i] - '0');

}

arr.push(num);

num = 0;

}

}

}

end = arr.top();

return end;

}

private:

stack<int> arr;

stack<string> brr;

};

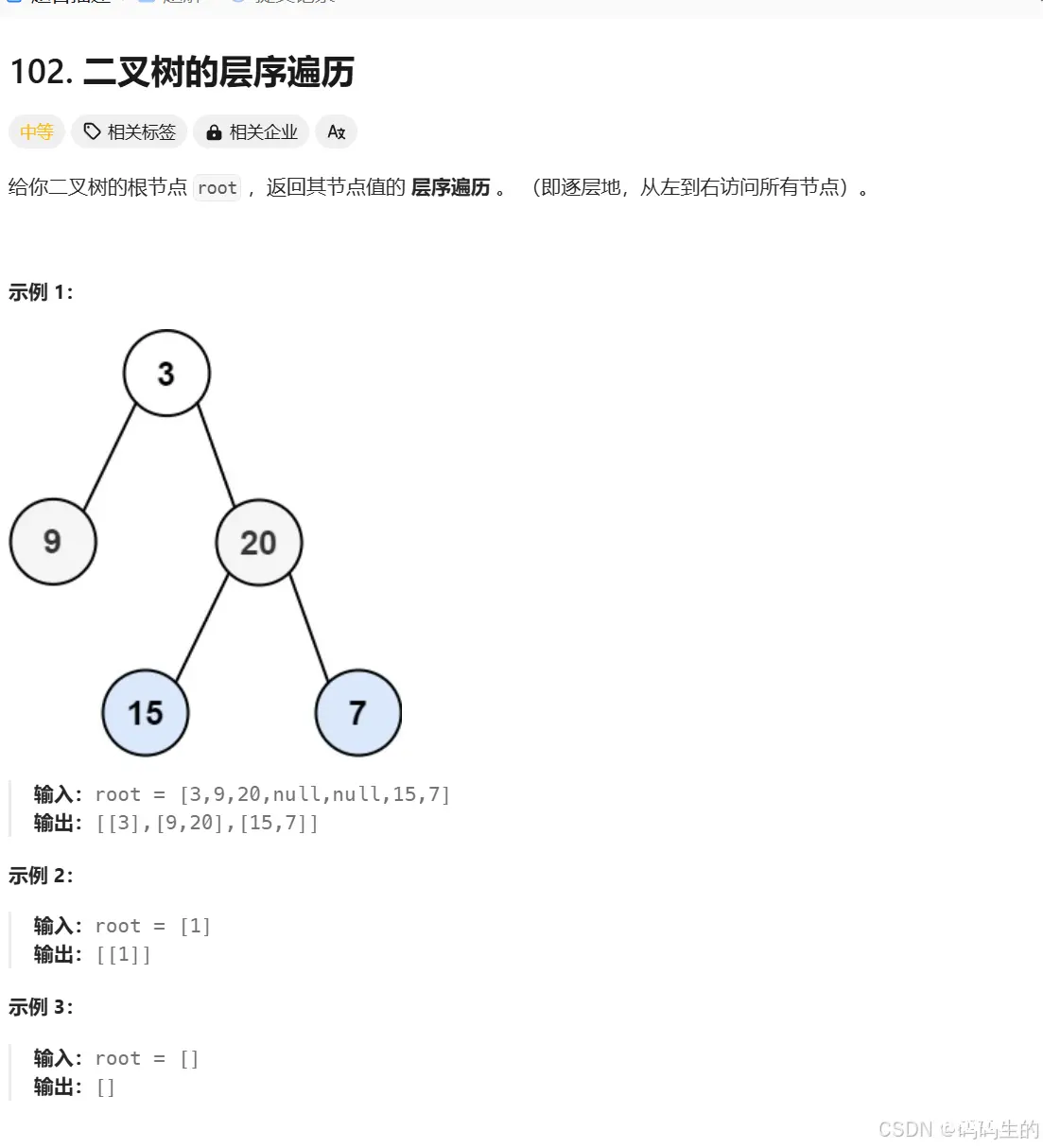
7.二叉树层序遍历 

. - 力扣（LeetCode）

<code>class Solution {

public:

vector<vector<int>> levelOrder(TreeNode* root)

{

vector<vector<int>> vv;

queue<TreeNode*> q;

int levelSize = 0; //记录某一层数据的个数

if(root != nullptr)

{

q.push(root);

levelSize = 1;

}

while(!q.empty())

{

//当前层数据的个数，控制数据一层一层的出

vector<int> v;

while(levelSize--)

{

TreeNode* front = q.front(); //保留队头指针

v.push_back(front->val); //尾差队头指针中的数据

q.pop(); //出队

if(front->left != nullptr) //左孩子不为空，入队

{

q.push(front->left);

}

if(front->right != nullptr) //右孩子不为空，入队

{

q.push(front->right);

}

}

vv.push_back(v);

//当前层出完，下一层都进队列了，队列的size就是下一层的数据个数

levelSize = q.size();

}

return vv;

}

};