CacheLab

文章目录

CacheLab实验概述一些前置准备Part A实验预览思路数据结构创建高速缓存从命令行中读取参数信息初始化高速缓存代码 读入内存操作指令解析地址映射代码 模拟高速缓存代码 释放内存代码 主函数代码 Part B实验预览32×32优化——分块8×8代码 优化——分块8×8+使用局部变量代码 64×64优化——分块8×8优化——分块4×4代码 优化——对8×8的块用4×4的方式处理1.0代码 优化——对8×8的块用4×4的方式处理2.0代码 61×67评分

“All problems in computer science can be solved by another level of indirection”

实验概述

实验分为两部分：Part A要求编写一个高速缓存模拟器（csim.c），Part B要求优化矩阵转置函数，最小化高速缓存的不命中的次数（trans.c）

这个实验设计得很好，恰好涵盖了书上第6章的两个核心部分：理解高速缓存的工作方式，以及编写高速缓存友好的代码，同时还应用到了p450页介绍的分块技术。建议先阅读以下的资料，再进行实验

CMU课件，最后有对Cache Lab的一些提示：rec07.pdf (cmu.edu)

分块技术的介绍：waside-blocking.pdf (cmu.edu)

讲解分块技术的博客：[读书笔记]CSAPP：16[VB]高速缓存存储器 - 知乎 (zhihu.com)

一些前置准备

按照实验说明，解压cachelab-handout.tar，创建出一个名为cachelab-handout的目录，这是我们Part A和Part B的工作目录，Part A对应的文件是csim.c，Part B对应的文件是trans.c

进到目录后先输入命令：make clean && make，这将会编译csim.c,trans.c,test-trans.c等文件

Part A

实验预览

Part A要求在csim.c文件中编写一个高速缓存模拟器，traces目录下的5个.trace文件是模拟器要执行的内存操作

老师提供了一个可供参考的缓存模拟器：csim-ref，这个模拟器有6个参数：

Usage: ./csim-ref [-hv] -s <s> -E <E> -b <b> -t <tracefile> • -h: Optional help flag that prints usage info • -v: Optional verbose flag that displays trace info • -s <s>: Number of set index bits (S = 2^s is the number of sets) • -E <E>: Associativity (number of lines per set) • -b <b>: Number of block bits (B = 2b is the block size) • -t <tracefile>: Name of the valgrind trace to replay

和书上使用的参数一致：s是组索引位数，E是每个组包含的高速缓存行的个数，b是块偏移位数，除此之外，参数v表示要详细输出每次内存执行时，高速缓存的模拟情况（命中、不命中、替换）；参数t是用于模拟内存操作的.trace文件名，举个例子：

./csim-ref -v -s 2 -E 2 -b 3 -t traces/yi.trace

这表示用csim-ref模拟一个高速缓存，执行traces/yi.trace的内存操作。我们设定这个高速缓存有4个组，每个组有2个高速缓存行，每个高速缓存块有8个字节

查看一下yi.trace中的内存操作：

L 10,1 M 20,1 L 22,1 S 18,1 L 110,1 L 210,1 M 12,1

内存操作的格式为：[space]operation address, size，operation 有 4 种：

I表示加载指令，表示从内存中读取指令内容L 加载数据，表示程序从某个内存地址加载了数据。（缓存命中、不命中、执行替换策略）S存储数据，表示程序向某个内存地址存储了数据。（写回、写分配）M 修改数据，表示程序对某个内存地址的数据进行了修改。

不需要考虑加载指令I,M指令相当于先进行L再进行S，模拟器要做出的反馈有 3 种：

hit：命中，表示要操作的数据在对应组的其中一行miss：不命中，表示要操作的数据不在对应组的任何一行eviction：驱逐，表示要操作的数据的对应组已满，进行了替换操作，这个实验的驱逐策略是LRU，选择最后被访问的时间距现在最远的块（CSAPP p423页）

Part A要做什么： 编写csim.c，这个程序的执行效果要与csim-ref相同，能够模拟一个高速缓存器（参数自定义），执行traces/xx.trace中的内存操作过程。这个模拟器不需要真的存储数据，只是计算traces/xx.trace的内存操作过程中，缓存的命中、不命中、LRU替换的数量，然后将这些参数作为答案，传给printSummary函数

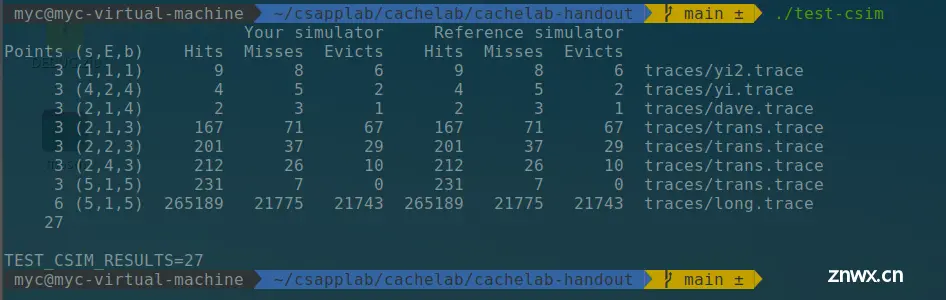
如何检验模拟器的正确性： 首先编译csim.c文件，命令为：gcc -o csim csim.c cachelab.c -lm，这将创建可执行文件csim，也就是你的模拟器

有两种检验方法：

使用csim-ref作为参考。设定相同的参数，分别用csim-ref和csim作为模拟器，读取同一个.trace文件的内存操作过程，比对两个模拟器输出的hit、miss、eviction的值使用评分程序test-csim，命令为：./test-csim，这个程序将会使用不同的参数设定你的模拟器，并让模拟器执行目录traces中所有的.trace文件，满分是27

思路

我将整个高速缓存模拟器的实现分为3个部分：

创建高速缓存：这包括从命令行中读取参数信息，初始化缓存读入内存操作：就是读取xx.trace文件中每行的内容根据读入的内存操作，模拟高速缓存的行为：核心代码，这包括在高速缓存中查找地址所指示的字，对不命中的处理（是加载到一个空的缓存行还是需要执行LRU替换策略）。每次执行一次缓存(caching)，就更新缓存(cache)信息（有效位、标志位、时间戳），同时统计hit、miss、eviction

数据结构

根据CMU课件的提示，我使用二维结构体数组实现cache。结构体定义如下：

typedef struct{ bool valid; //有效位 unsigned long tag; //标志位 int timestamp; //时间戳}cache_line; //一个高速缓存行

定义二维结构体数组为cache_line** cache，这个数组的大小是S×E，cache[i]是高速缓存组i，cache[i][j]是高速缓存组i中的高速缓存行j，cache[i][j]中包含有效位（valid）、标志位（tag）、时间戳（timestamp，记录这个高速缓存行最后被访问的时间），由于不需要存储数据，就没有定义高速缓存块

创建高速缓存

从命令行中读取参数信息

由于s、E、 b是由命令行参数设定的，所以要先读取命令行中的参数，可以使用课件中提示的getopt函数，参考getopt(3) - Linux manual page (man7.org)

为了便于访问参数s、E、b，我使用全局变量定义这些参数，简化代码。同时，我使用变量verbose来标识是否需要详细输出缓存过程

这里说一个小坑，getopt函数中，没有参数的选项不带":"，如果你写成了v:s:E:b:t，即不带参数的-v有了":"，那么getopt就会等待参数的输入。当opt为s时，会将读到的参数optarg给v，而不是后出现的s，这就是说，-v将-s的参数作为自己的参数，-s就直接被跳过了，然后后面就正常读了，所以E、b、t都没问题，只有s为0（花费我1h用gdb来回调试才发现的bug😢，这样的细节很要命）

初始化高速缓存

为结构体数组分配空间： 相应的，二维结构体数组的空间也是动态分配的。根据读入的参数s、E、b，使用malloc分配内存

初始化高速缓存： 将cache[i][j]的有效位（valid）设置为0，表示这是一个空的高速缓存行；时间戳（timestamp）设置为0

代码

实现的代码如下：

cache_line** create_cache(int argc, char** argv){ int opt; while(-1 != (opt = getopt(argc, argv, "vs:E:b:t:"))) { switch(opt) { case 'v': verbose = 1;//设置verbose为1，表示要详细输出缓存过程 break; case 's': s = atoi(optarg); break; case 'E': E = atoi(optarg); break; case 'b': b = atoi(optarg); break; case 't': strcpy(t, optarg); break; default: break; //程序健壮性检验，如果不是一个合法的参数，就会退出switch,继续while读取 } } //申请内存，创建高速缓存，组数为2^s,每一组高速缓存行总数为E个。即创建一个行为2^s,列为E的二维结构体数组 int row = pow(2, s); int col = E; cache_line** cache = (cache_line**)malloc(row*sizeof(cache_line*)); if(cache == NULL) { printf("Failed to allocate memory!\n"); exit(1); } for(int i=0; i<row; ++i) { cache[i] = (cache_line*)malloc(col*sizeof(cache_line)); if(cache[i] == NULL) { printf("Failed to allocate memory!\n"); exit(1); } } //初始化高速缓存，设置有效位为0，时间戳为0 for(int i=0; i<row; ++i) { for(int j=0; j<col; ++j) { cache[i][j].valid = 0; //有效位 置0 cache[i][j].timestamp = 0; } } return cache;}

读入内存操作

我们要模拟的内存操作过程放在了xx.trace文件中，这个文件的名称由命令行参数提供，存放到字符数组t中。读入内存操作 就等价于 读取文件t的每一行，对指令进行解析，然后获取地址映射的组索引、标记，用于后续在模拟高速缓存时，在高速缓存中查找这个地址的内容

使用课件中建议的fscanf函数，读取文件t的每一行指令。

指令解析

指令的形式为：[space]operation address, size，根据实验预览部分的分析，我们只需要读取指令L、S、M，而M等同于先L，再S，所以指令M需要进行两次缓存

地址映射

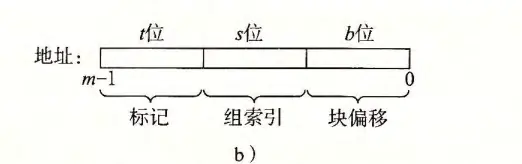
参照书上对地址的划分方法，将读到的地址addr进行掩码运算，获得该地址映射的组索引set和标记tag:

set = (addr>>b) & (unsigned long)((1<<s)-1);tag = addr >> (b+s);

代码

void get_trace(cache_line** cache){ FILE *fp = fopen(t, "r"); if(fp == NULL) { perror("Error opening file"); exit(1); } char operation; unsigned long addr; int bytes; //地址映射的组号和标志位 int set; unsigned long tag; while(fscanf(fp, " %c %lx,%d", &operation, &addr, &bytes) == 3) { set = (addr>>b) & (unsigned long)((1<<s)-1); tag = addr >> (b+s); switch(operation) { case 'L': case 'S': if(verbose) printf("%c %lx,%d ", operation, addr, bytes); cache_simulate(cache, set, tag); if(verbose) printf("\n"); break; case 'M': if(verbose) printf("%c %lx,%d ", operation, addr, bytes); cache_simulate(cache, set, tag); cache_simulate(cache, set, tag); if(verbose) printf("\n"); break; default: break; } }}

模拟高速缓存

根据从内存操作中由地址映射的组索引set、标记tag，模拟缓存过程

为了简化参数，我使用一个数组result[3]来存放hit、miss、eviction的次数。

为了记录缓存行cache[i][j]最后被执行的时间，即设置时间戳cache[i][j].timestamp，我使用一个全局变量T作为整体的时间。初始 T设置为0，每当进行一次缓存(caching)，就要对T加1，这样当需要进行LRU替换时，我们遍历查找这个组，驱逐时间戳最小的缓存行。恰好我们在每一次缓存(caching)后，使用update函数更新缓存(cache)的信息，所以当调用update函数时，就意味着进行了一次缓存(caching)，因此可以在update函数中对T加1，更新整体的时间

模拟高速缓存的整体逻辑是：

首先在高速缓存组cache[set]中进行行匹配：遍历检查缓存行cache[set][j]的有效位和标记位，以确定地址中的字是否在缓存中。如果找到了一个有效的行cache[set][pos]，它的标记与地址中的标记tag相匹配，则缓存命中；若遍历了所有的行都不匹配，则为缓存不命中若缓存命中，则直接调用update函数，更新时间戳：cache[set][pos].timestamp = T，并统计hit：result[HIT]++（这里我使用了枚举）若缓存不命中，则需要判断这个组cache[set]是否满了，一种方法是维护一个数组occupancy，它记录了各个组中有效位为1的有效行个数，初始置为0。比较occupancy[set]（有效行个数）与E（行总数），判断缓存组cache[set]中是否还有空行 若occupancy[set] < E，则有空行。只需要遍历cache[set]中各个行的有效位，找到空行（设空缓存行是cache[set][pos]），然后调用update函数，将cache[set][pos]的有效位置1：cache[set][pos] = 1；标记位更新为tag：cache[set][pos].tag = tag；更新时间戳：cache[set][pos].timestamp = T；统计miss：result[MISS]++若occupancy[set] == E，则没有空行，需要执行LRU替换策略。调用函数LRU_replace，遍历整个组cache[set]，找到时间戳最小的缓存行，返回这个缓存行的位置pos，然后调用update函数，更新cache[set][pos]（同上），并统计eviction：result[eviction]++

代码

//核心代码void cache_simulate(cache_line** cache, int set, unsigned long tag){ bool find = false;//标识是否命中 int col = E; int pos = 0; for(int j=0; j<col; ++j) { //命中了(有效位为1，且与某一个高速缓存行的标志位匹配上了) if(cache[set][j].valid == 1 && cache[set][j].tag == tag) { pos = j; //对高速缓存行j进行更新 update(cache[set], HIT, pos, tag); find = true; break; } } //如果没有命中，则先检验这个组是否满了,通过维护一个数组occupancy，可以获得组set中有效缓存行的数量 if(!find) { //如果还有空的缓存行，则直接将内存块存放到这个空白行中 if(occupancy[set] != E) { occupancy[set]++; //要加载内存块到一个空缓存行中，占用量+1 for(int j=0; j<col; ++j) //寻找一个空白行，将内存块“加载”到这个缓存行中 { if(cache[set][j].valid == 0) { pos = j; update(cache[set], MISS, pos, tag); break; } } }else //如果整个组都满了，没有空白行，则此时需要用LRU策略替换掉一个缓存行 { pos = LRU_replace(cache[set]); //获取要被替换的行号 update(cache[set], MISS, pos, tag); update(cache[set], EVICTION, pos, tag); //更新 } }}//更新void update(cache_line* cache_set, enum Category category, int pos, int tag){ void update(cache_line* cache_set, enum Category category, int pos, int tag){ result[category]++;//统计相应的缓存情况（命中、不命中、替换） printf("%s ", category_string[category]); cache_set[pos].tag = tag;//更新标志位 cache_set[pos].valid = 1;//更新有效位 cache_set[pos].timestamp = T;//更新时间戳 T++; //每次更新，都要增加时间T}}//LRU替换,暴力搜索时间戳最小的缓存行，返回行号posint LRU_replace(cache_line* cache_set){ int min = cache_set[0].timestamp; int pos = 0; for(int j=1; j<E; ++j) { if(cache_set[j].timestamp < min) { pos = j; min = cache_set[j].timestamp; } } return pos;}

释放内存

良好的编程习惯，手动释放内存

代码

void destory(cache_line** cache){ int row = pow(2, s); for(int i=0; i<row; ++i) { free(cache[i]); } free(cache);}

主函数

代码

int main(int argc, char** argv){ cache_line** cache = create_cache(argc, argv); get_trace(cache); destory(cache); printSummary(result[0], result[1], result[2]); return 0;}

完整代码见github仓库：y-tanx/csapp: csapp lab,including solutions and explanations (github.com)

运行结果：

评分：

Part B

实验预览

Part B要优化一个矩阵转置函数，尽可能减少miss次数，要修改的文件是trans.c，高速缓存的参数：s=5,E=1,b=5，这个高速缓存共有32组，每组有一行（直接映射），每一行存32字节，即8个int

Part B很有意思，虽然矩阵转置的时间复杂度始终为O(n^2)，但是可以利用高速缓存和程序局部性，对矩阵转置函数进行优化

要进行转置的矩阵有三种：

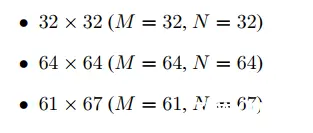
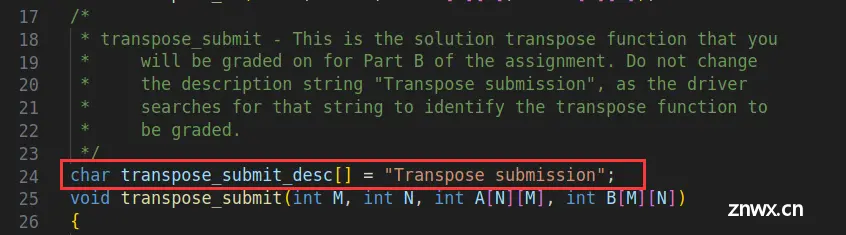
Part B要做什么： 在trans.c中，使用分块技术优化矩阵转置函数，处理三个不同的输入，你要将优化后的函数写到这一行的下面：

如何检验优化的效果： 首先在目录中使用：make clean && make，编译trans.c、test-trans.c

然后使用命令：

make && ./test-trans -M 32 -N 32 make && ./test-trans -M 64 -N 64 make && ./test-trans -M 61 -N 67

分别检验三种规模的矩阵转置时的优化情况

评分标准如下，以缓存不命中的次数misses作为优化的指标：

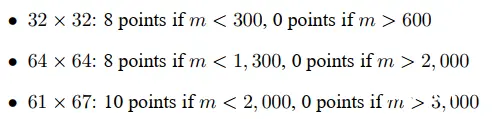
也可以使用命令：

./csim-ref -v -s 5 -E 1 -b 5 -t trace.f0 > hitf

在文件hitf中，查看内存的实际访问情况

32×32

trans.c文件中提供了一个原始的转置方法trans，我们可以将它复制到transpose_submit中，检验一下效果：

测试如下：

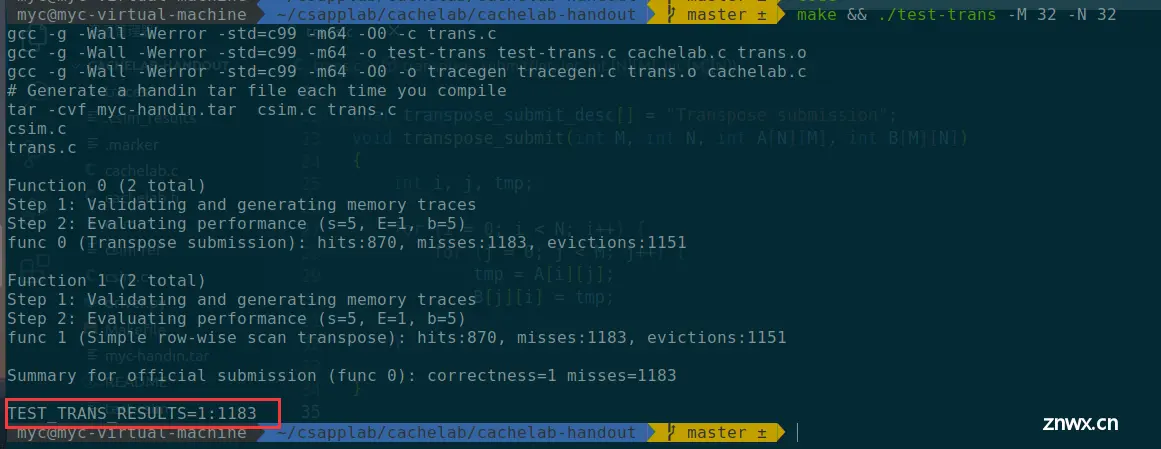
测试结果是1:1183，不命中的数量是很大的

分析不命中出现在哪里：

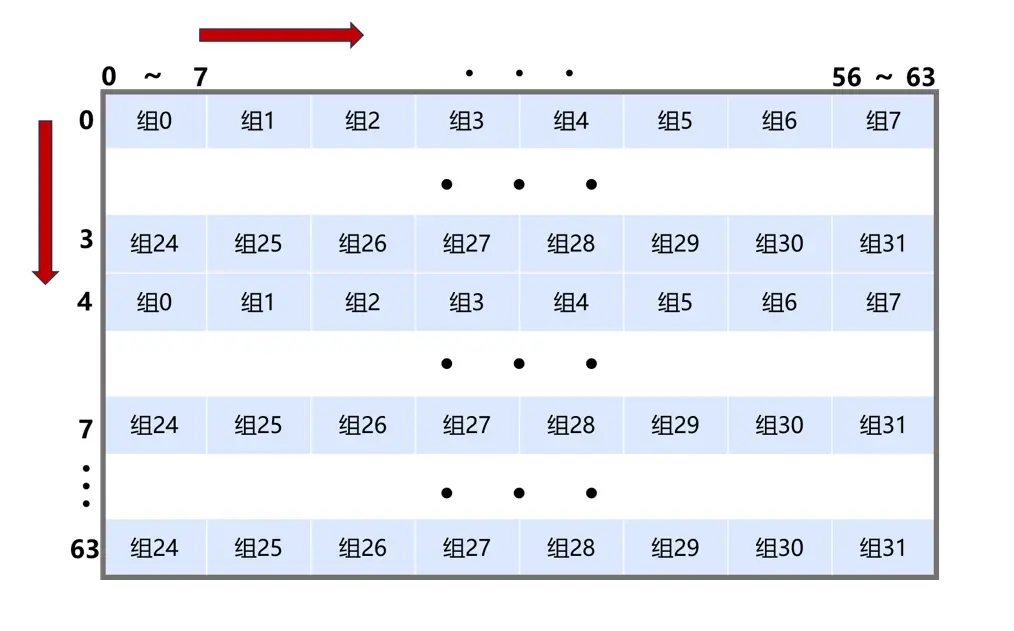
假设A[0][0]的地址为0x0，B[0][0]的地址为0x1000（这是合理的，hitf文件中显示A、B的地址相差64的倍数）。可以看到，每8个元素映射到同一个缓存组，每一行的元素（32个）能映射到相邻的4个缓存组，按行来看：A[0]~A[7]这8行依次映射到组0 ~ 组3、组4 ~ 组7， 组8 ~ 组11，组12 ~ 组15，组16 ~ 组19，组20 ~ 组23，组24 ~ 组27，组28 ~ 组31。在第9行，A[8]与A[0]映射的缓存组相同（可以通过地址来看，每256个元素的组索引相同，会映射到同一个组），所以每隔8行，映射的缓存组相同。按列来看：B[0]与B[1]中的同一列元素相差4个缓存组，如B[0][0]映射到组0，B[1][0]映射到组4。同样的，同一列的元素每隔8行，就会映射到同一个缓存组，比如B[0][0]与B[8][0]都映射到组0

数组A、B每部分映射的缓存组如下图所示：

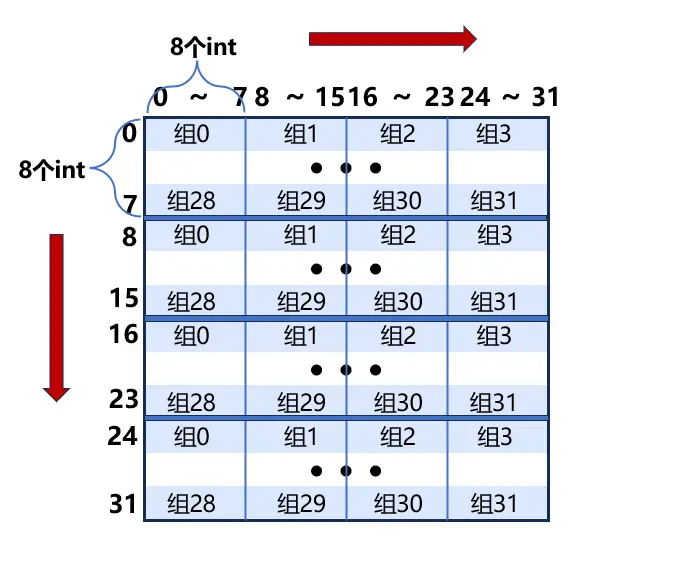
由上述的分析可知，在按行遍历数组A时，访问每组的首个元素时，会发生冷不命中（发生在A[0]~A[7]中）或 冲突不命中（A[8]之后），组中的其余元素不会再产生miss（对角线元素特殊，后面会讲解），共有(32×32)/8=128次miss

在按列遍历数组B时，当我们访问到B[i][j]时，我们将B[i][j]存放到它映射的缓存组中，设这个缓存组为组a，此时产生了一次不命中。由于要按列遍历，同一列元素相差4个缓存组，所以缓存组a不会再存放其它的数据，此时缓存组a的块只存放了一个元素B[i][j]。当遍历到同一列的B[i+8][j]时，由于同一列的元素每隔8行，就会映射到同一个缓存组，所以B[i+8][j]与B[i][j]均映射到缓存组a，此时访问B[i+8][j]会发生冲突不命中。由于组a中只有一个缓存行（直接映射缓存组），所以会将B[i][j]驱逐。当再次循环，遍历到B的下一列元素B[i][j+1]时，由于B[i][j]被驱逐了，组a中存放其它的元素，所以访问B[i][j+1]仍然不命中。因此，访问B中的每个元素时都不命中，总共有32×32=1024次miss

对于对角线元素，对角线元素A[i][i]与B[i][i]会映射到同一个高速缓存组（可以分析地址，A[i][i]与B[i][i]地址的组索引相同），设这个缓存组为组b。当访问到B[i][i]时，高速缓存组b已经存放了A[i][i]，所以B[i][i]会驱逐A[i][i]（这没有增加B的miss，因为上述分析中，访问B中的每个元素都不命中，接下来访问的B[i][i+1]不会映射到组b，所以访问B[i][i]只有一次不命中，被记入到1024次miss中了），但是接下来要访问A[i][i+1]，此时组b中存放的是B[i][i]，所以会再将B[i][i]驱逐，造成了A额外的一次冲突不命中。对角线元素有32个，最后一个对角线元素A[31][31]在块C的末尾，当访问B[31][31]时，会驱逐块C中的A[31][31]。但是在访问B[31][31]后，程序结束了，所以这次不会发生A额外的冲突不命中，因此共有31次额外的miss

总计，有128+1024+31=1183次miss，正好符合我们实际检验的值，这验证了上述分析的正确性

注意，上面的分析可看可不看，不会影响接下来的优化。但是自己画图，真正做一次这样的分析，尤其是分析对角线元素的相互驱逐，会加深你对缓存的理解，也能更清楚为什么我们要分块——增加块的利用率，从而减少不命中率。所以建议你试着画图，分析一下缓存过程，如果有问题再看我上面的分析

好了，分析这么多该开始想想怎么优化了

性能瓶颈：通过上面的分析，我们发现矩阵B对缓存的利用率很低，每次缓存组只存放B中一个元素，而且在后续访问这一列时，这个元素就被驱逐了，造成了每个元素读取一次，就会发生一次不命中的情况。而分块的核心思想就是：将一个程序中的数据结构组织成大的片（Chunk），使得能够将一个片加载到高速缓存中，并在这个片中多次进行读写，提高对缓存的利用率，分块技术正好对症！

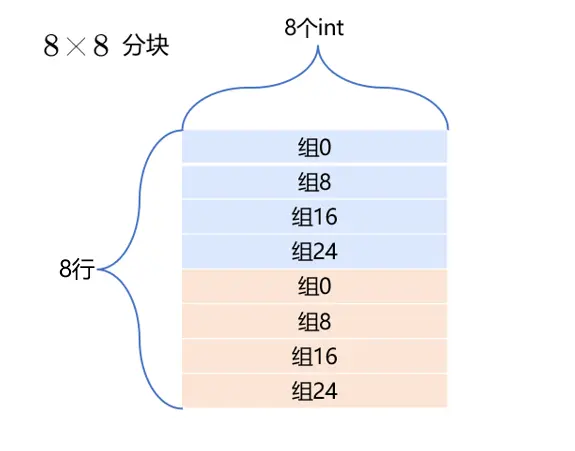
优化策略：增加矩阵B对缓存的利用率，最好的情况就是每个缓存块中的8个位置都填入了B的元素，所以首先考虑8×8分块，一次循环对8×8的元素块进行转置

优化——分块8×8

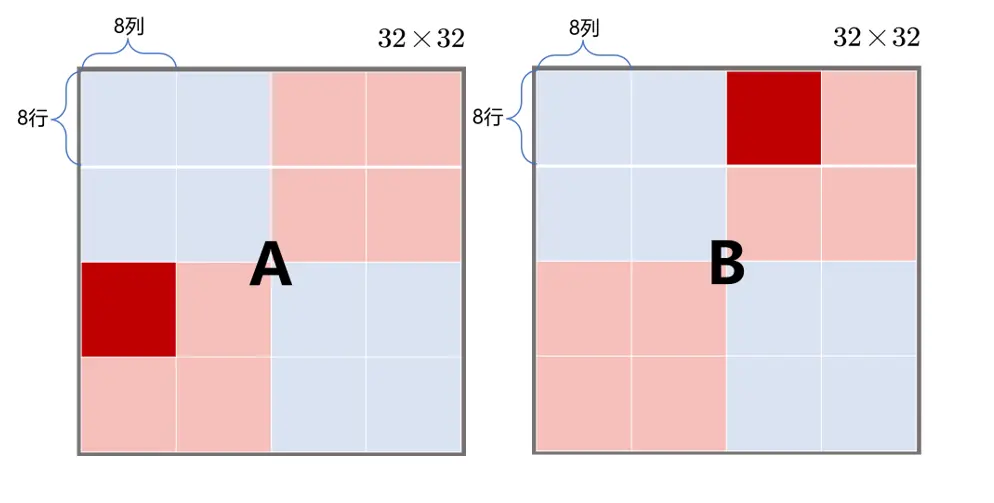
图模仿知乎博主：大猫咋，链接：(99+ 封私信 / 40 条消息) 大猫咋 - 知乎 (zhihu.com)，感谢学长优秀的文章

一次取出8×8的元素，由4个高速缓存组存储。8×8分块在块的内部不会造成冲突，A与B的高速缓存组正好错开了（A、B两个红色块映射的高速缓存组没有交集），而且充分利用了块的内存空间。核心在于降低了B的不命中率：原来要存放32个元素，有32次不命中；现在存放64个元素，有8次不命中，降低不命中率至1/8（除对角线块外，但对角块经过优化，只有一个对角元素不命中，所以不命中率也近似于1/8），所以优化是有效的

代码

void transpose_submit(int M, int N, int A[N][M], int B[M][N]){ // 使用分块8×8的方法来进行转置 for(int i=0; i<M; i+=8) { for(int j=0; j<N; j+=8) { for(int s=0; s<8; ++s) { for(int k=0; k<8; ++k) { B[j+k][i+s] = A[i+s][j+k]; } } } }}

对于A中每一个操作块，只有每一行的第一个元素会不命中，所以为8次不命中；对于B中每一个操作块，只有每一列的第一个元素会不命中，所以也为 8 次不命中。总共miss次数为：8 × 16 × 2 = 256

看一下结果：

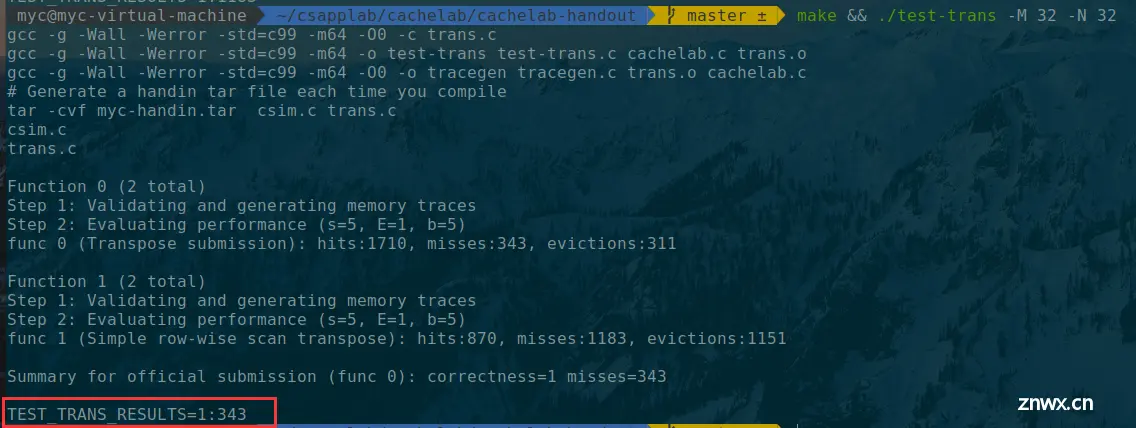
miss的次数是343，比理论高了太多，这是什么原因？

性能瓶颈： 和分析trans函数一样，我们还需要分析对角线上的块。首先使用命令./csim-ref -v -s 5 -E 1 -b 5 -t trace.f0 > hitf，查看一下hitf

我们会发现A和B的地址的差距是0x40000(64的整数倍)，所以当操作块Ap、Bq位于对角线上时，存放两个块所用的4个缓存组相同，因此加载块Ap 和存储块Bq会一直发生驱逐，原因就在于需要不断加载块Ap来读取下一个元素。如果要避免这种情况发生，可以利用局部变量存储块Ap的一行，这么做，即使当存储块Bq时，驱逐了块Ap的这一行，后续也不需要再加载Ap的这一行，而直接使用保存在局部变量中的数据赋给块Bq

优化策略：考虑使用 8 个本地变量一次性存下 A 的一行后，再复制给 B

优化——分块8×8+使用局部变量

代码

void transpose_submit(int M, int N, int A[N][M], int B[M][N]){ //由于对角线部分的冲突不命中增多，导致miss的数量较大，使用的方法是将A中的一组元素（8个）使用局部变量存储在程序寄存器中，避免了A和B的加载和写回的冲突不命中 int a0, a1, a2, a3, a4, a5, a6, a7; for(int i=0; i<N; i+=8) { for(int j=0; j<M; j+=8) { //将一组的8个Aij都存放到寄存器文件中，然后直接传递给Bji，对于对角线元素虽然仍有冲突，但是除此之外，对角线块不会出现冲突 //估计约287misses（256+31），这种方法只有处在对角线上的元素会出现冲突 for(int k=0; k<8; ++k) { a0 = A[i+k][j+0]; a1 = A[i+k][j+1]; a2 = A[i+k][j+2]; a3 = A[i+k][j+3]; a4 = A[i+k][j+4]; a5 = A[i+k][j+5]; a6 = A[i+k][j+6]; a7 = A[i+k][j+7]; B[j+0][i+k] = a0; B[j+1][i+k] = a1; B[j+2][i+k] = a2; B[j+3][i+k] = a3; B[j+4][i+k] = a4; B[j+5][i+k] = a5; B[j+6][i+k] = a6; B[j+7][i+k] = a7; } } }}

结果：

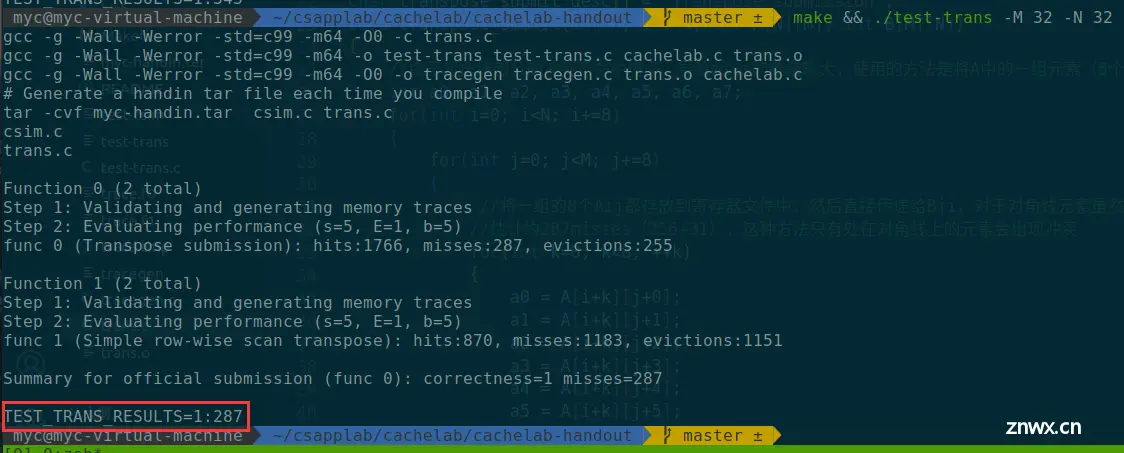
miss：287，满分！

64×64

这个很难，我想了好久，也是逐渐优化的

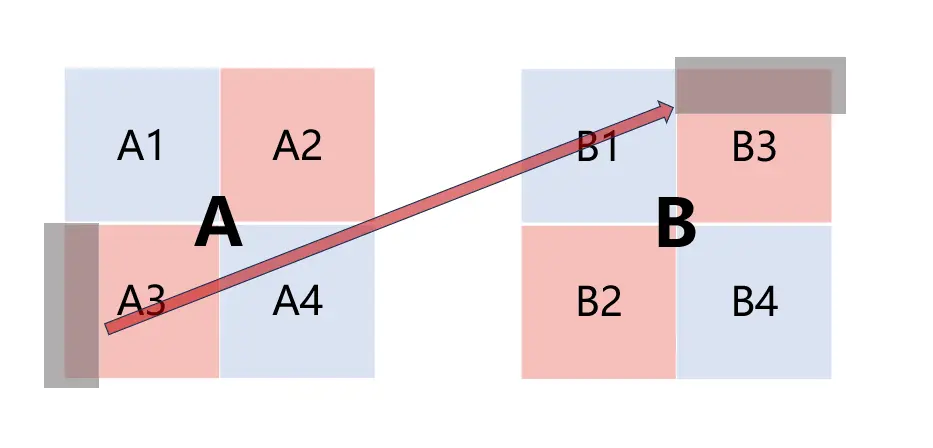
每8个int为1组，每一行（64个int）有8组，每4行就会映射到相同的组，如A[0][0]映射到组0，A[4][0]也映射到组0；同一列的元素之间相差9组，如A[0][0]映射到组0，A[1][0]映射到组8

优化——分块8×8

和前面的一样，先是考虑8×8分块，但是发现8×8块的内部会出现冲突，如图所示：

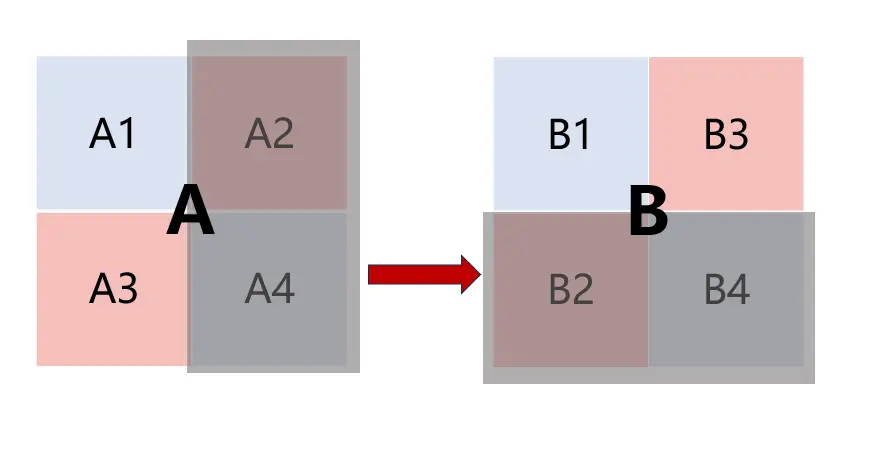
性能瓶颈：以A中左上角的块为例，加载这个块需要缓存组0、组8、组16、组24，然后又要重新从缓存组0开始做，这对于A没有什么影响，因为A是按行转置的，每一行都转置完了，才读下一行，所以加载块A的miss不会增多。但是对B中的块就不同了，以B中右上角的块为例，由于每4行 组索引正好重复，存储这个块需要缓存组7、组15、组23、组31，然后又要重新从缓存组7开始。而B是按列写入的，每一次循环都会从上至下，依次映射到缓存组7、组15、组23、组31，然后又重新映射到缓存组7。这会出现和trans函数中一样的情况： 写入每一列时，都会先驱逐前4个行的高速缓存，才能写入后4个行；而开始写入前4个行时，此时前4行映射的高速缓存组中，存放了A的数据，所以要先驱逐保存A的高速缓存，然后再写入前4行（也是因为组的映射相同，当遍历完A的前8行时，缓存组0~31号均有A的内容，此时B在遍历前8列，映射的组号始终为0、8、16、24）。最终导致写入B的每个元素，都会产生一次miss

结果：

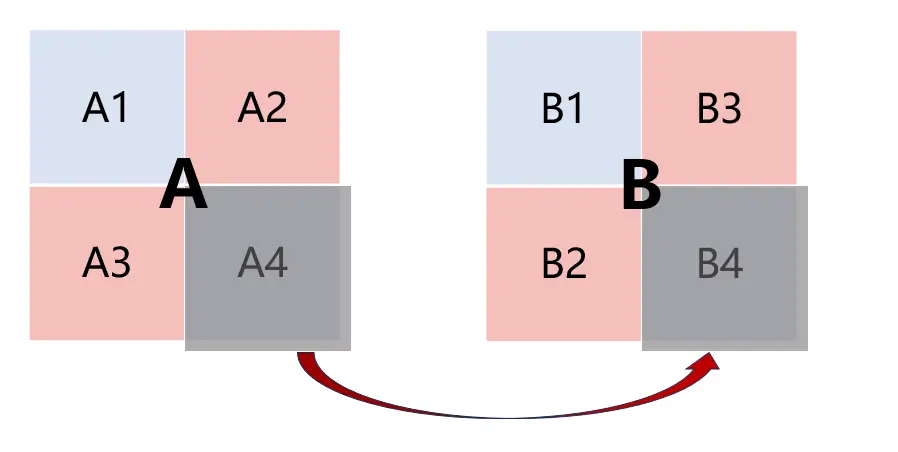
果然，miss的个数为4611，是一个很大的数

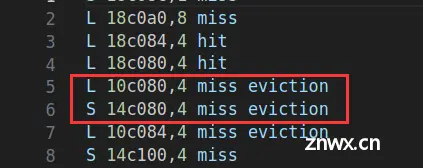
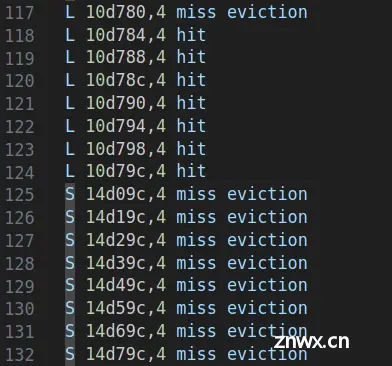
查看一下hitf：

可以看到当保存B的块时，会出现连续8个S的miss eviction

模拟：

前4个miss eviction： 当写入B[0][56]~B[7][56]这一列时，前4行B[0][56]~B[3][56]映射的组号为7、15、23、31（假设B数组起始地址为0x1000），在此之前，A曾经使用过组号为7、15、23、31的高速缓存组，所以此时这4个组中保存了A中的数据，此时发生冲突不命中，需要将这4个组中A的数据驱逐，然后再写入B[0][56]~B[3][56]的数据

后4个miss eviction： 对于后4行B[4][56]~B[7][56]，它们映射的组号也为7、15、23、31，而此时这4个组保存了这个块的前4行B[0][56]~B[3][56]中的数据，此时发生冲突不命中，需要将这4个块中B的数据驱逐，然后再写入B[4][56]~B[7][56]的数据

优化策略： 主要的不命中来源于B中的块，原因在于块的内部有冲突，下面行的元素会驱逐上面行的元素。前4个miss无法避免，但是后4个miss是可以优化的，我们分块的目的就是实现对这个块中偏重读写，充分利用高速缓存的空间，从而减少不命中率，所以考虑4×4分块

优化——分块4×4

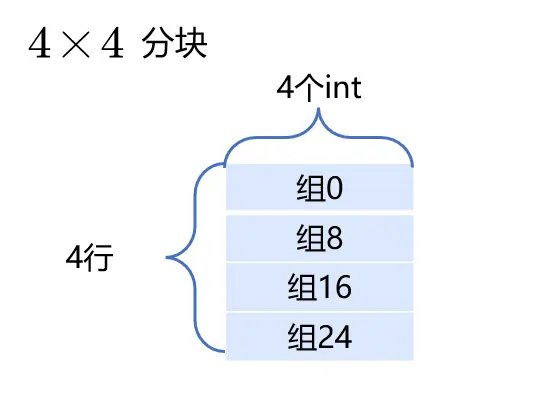
此时4×4块的内部不会发生冲突，A与B之间相应的操作块也不会发生冲突

代码

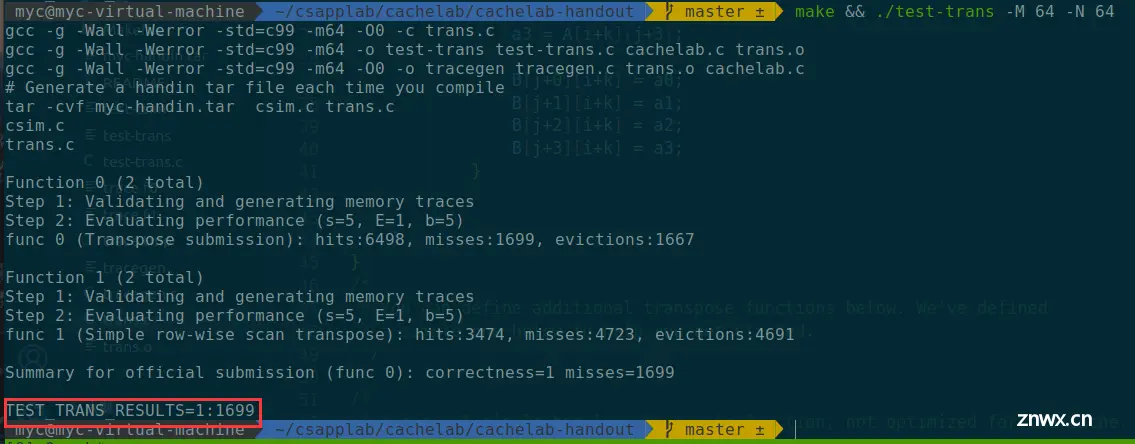
void transpose_submit(int M, int N, int A[N][M], int B[M][N]){ int a0, a1, a2, a3; for(int i=0; i<N; i+=4) { for(int j=0; j<M; j+=4) { for(int k=0; k<4; ++k) { a0 = A[i+k][j+0]; a1 = A[i+k][j+1]; a2 = A[i+k][j+2]; a3 = A[i+k][j+3]; B[j+0][i+k] = a0; B[j+1][i+k] = a1; B[j+2][i+k] = a2; B[j+3][i+k] = a3; } } }}

结果：

miss：1699，优化的效果很好，但是没有达到满分，说明还有优化的空间

查看一下hitf：

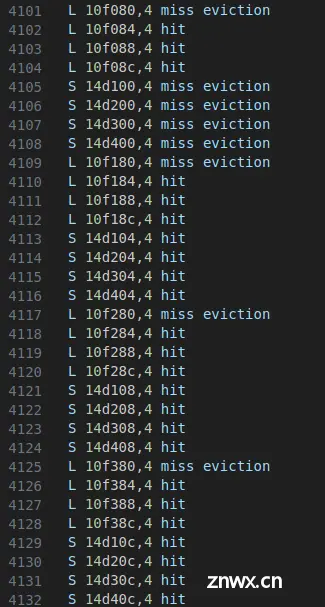
性能瓶颈：对于A中每一个操作块，只有每一行的第一个元素会不命中，所以为4次不命中；对于B中每一个操作块，只有每一列的第一个元素会不命中，所以也有4次不命中。使用4×4分块，确实避免了块内部的冲突，但是浪费了每个缓存块中其他4个元素的空间，这会导致不命中率增加——每加载 或 存储4个元素，就有1次miss。而使用8×8分块，在块内部不冲突的前提下，每加载 或 存储8个元素，才有1次miss

优化策略：虽然4×4的方法还有不尽人意的地方，但是它给了我启发：可以尝试先存储B中8×8块的前4行，当所有转置的结果都存放到B的前4行时，再对后4行存储。关键在于不要使B的块因为上下4行的组索引相同的原因，导致被来回替换

PS：我在做完64×64的优化时看了一下别人的博客，他们给最终的优化方法起了一个好玩的名字：“对8×8的块用4×4的方式处理”，所以尽管接下来的优化版本不是最终的答案，但是不能否认4×4的方法确实给了我很大的启发，因此它也可以称为“对8×8的块用4×4的方式处理”

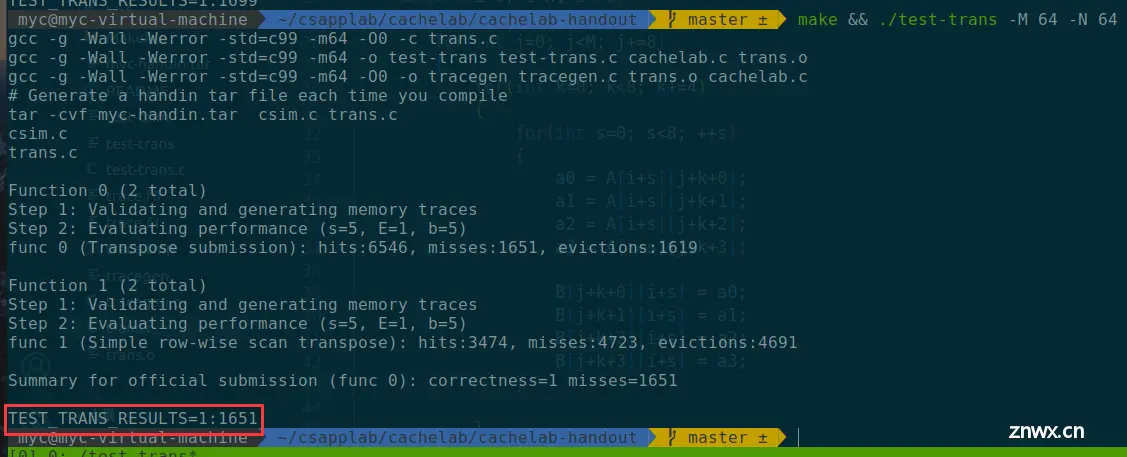
优化——对8×8的块用4×4的方式处理1.0

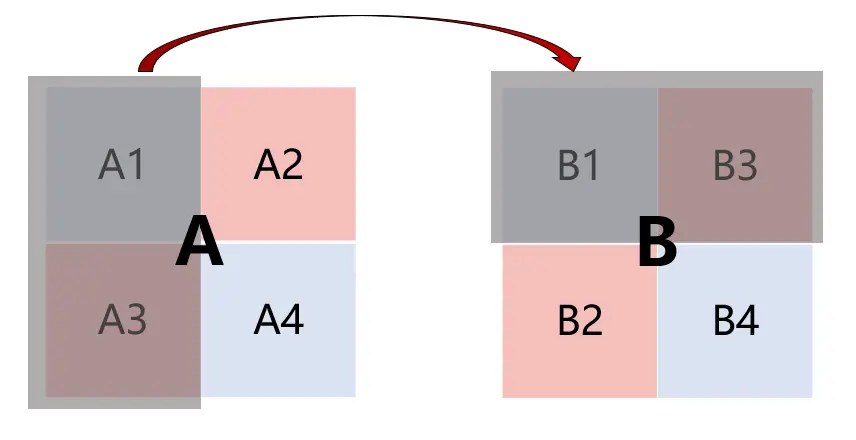
使用8×8分块，并将这个块分为四个4×4的块，然后按照特定顺序进行转置：先处理B中块的前4行B1、B3，当所有转置的结果都存放到B的前4行B1、B3时，再处理B的后4行B2、B4

第一步，先处理B1、B3，将A1、A3的转置结果存放到B1、B3中

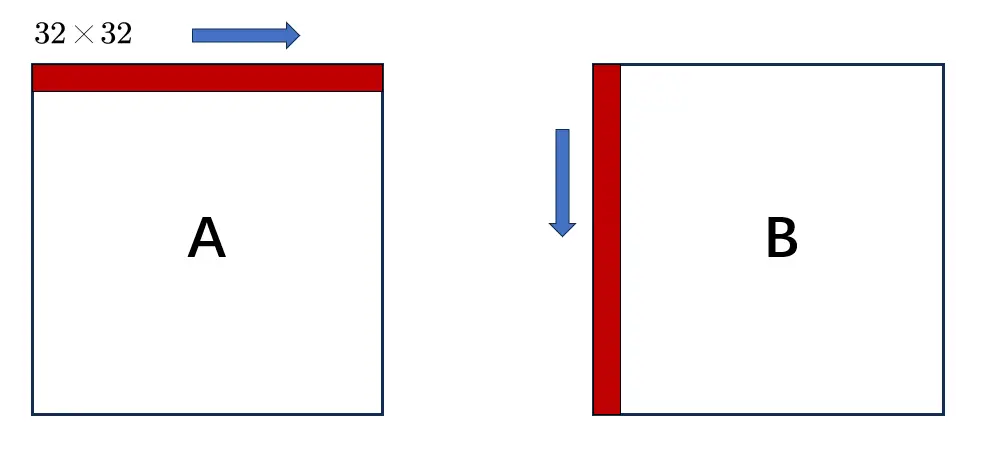
第二步，再处理B2、B4，将A2、A4的转置结果存放到B2、B4中

代码

void transpose_submit(int M, int N, int A[N][M], int B[M][N]){ int a0, a1, a2, a3; for(int i=0; i<N; i+=8) { for(int j=0; j<M; j+=8) { for(int k=0; k<8; k+=4) { for(int s=0; s<8; ++s) { a0 = A[i+s][j+k+0]; a1 = A[i+s][j+k+1]; a2 = A[i+s][j+k+2]; a3 = A[i+s][j+k+3]; B[j+k+0][i+s] = a0; B[j+k+1][i+s] = a1; B[j+k+2][i+s] = a2; B[j+k+3][i+s] = a3; } } } }}

结果：

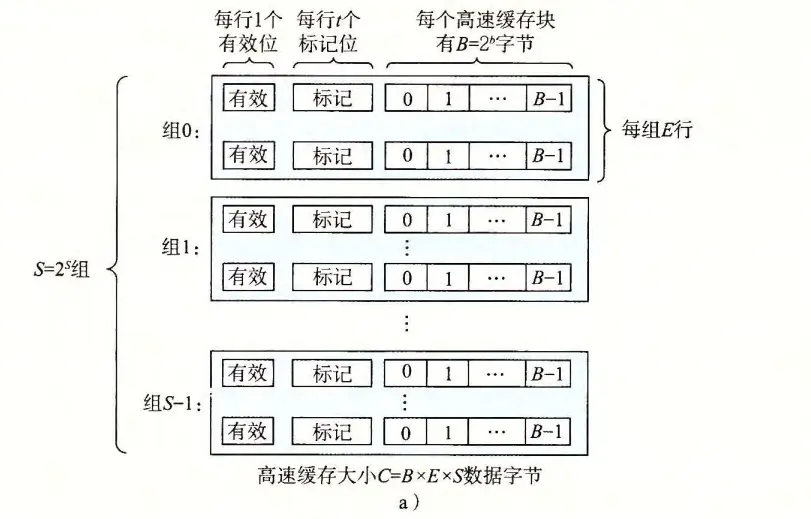
miss：1651，相较于上一个4×4分块的方法，没有优化太多，这是什么原因？

性能瓶颈： 分析一下这个程序，相较于最初的8×8分块，这个版本的优化使B的miss减少很多（填入B的8个元素，miss只有8个，即每组首个元素的不命中，这是无法避免的），但是对于A的miss没有减少，而且没有我们想象的“充分利用块的空间，取出来8个Aij”。由于转置受限，我们只能取出块Ap每一组中的前4个元素，依次赋给块Bq的前4行。当Bq的前4行都填满时，我们才能取出Ap每组中的后4个元素，对Bq的后4行进行填写，所以对Ap的8个组，每一组会有2次miss，加载A中一个8×8的块共有16次miss，平均每取出4个元素就会出现1次miss，根本没有达到我们的目标——充分利用块的空间，一次miss能取出8个元素

优化策略： 这对于8×8的情况已经提升不少——按照初始的8×8方法，加载块Ap和存储块Bq共需要8 + 64（Bq全不命中） = 72个miss。但是相对于4×4的方法，这种方法没有太大的提升。这种改进版本和4×4的方法都减少了B的miss，而且效果等同：改进版本填入8个Bij有8次miss，而4×4分块中填入4个Bij有4次miss。但是4×4的方法就到这里了，而改进的方法还能被优化，因为我们能充分利用上高速缓存块中A的8个元素——一次取出高速缓存块中A的8个元素，4×4显然做不到。所以我们接下来对改进版本再优化，使它能一次取出高速缓存块中A的8个元素

优化——对8×8的块用4×4的方式处理2.0

这个部分我试了很长时间，但是大致方向始终没有错误：利用4×4方法对8×8的块进行处理，按照特殊的转置方法，避开B的块内部的冲突

首先我想到要用8个变量存放块Ap的一行。存放A1的局部变量传递给B1，实现B1的转置；但是存放A2的局部变量只有传递给B2才能实现转置，而存储B2就会驱逐B1、B3部分，没有解决块Bq内部的冲突，而局部变量只能有12个，所以此时只有一个地方有空——B3，我只好把存放A2的局部变量传递给B3，此时B3中存放的是B2的转置结果，即A2^T

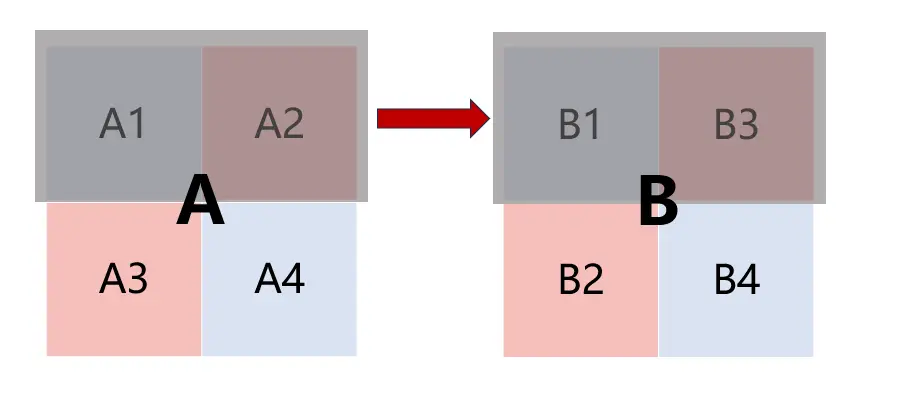
但是要驱逐B1、B3，保存B2、B4的前提是我不需要再修改B1、B3，所以我要在保存B2、B4之前，要将B3的转置结果填到B3中，这个过程很有技巧：

首先，将B3的一行存放到局部变量中

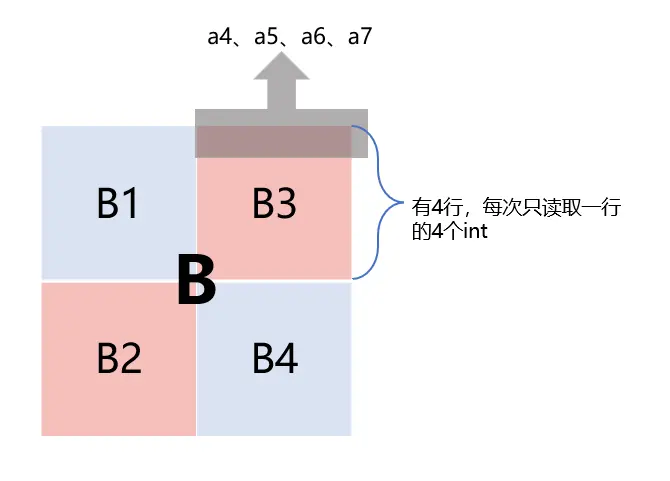
然后，将A3的一列填补到B3取出的这一行中，B3的这一行填入了对应的转置结果

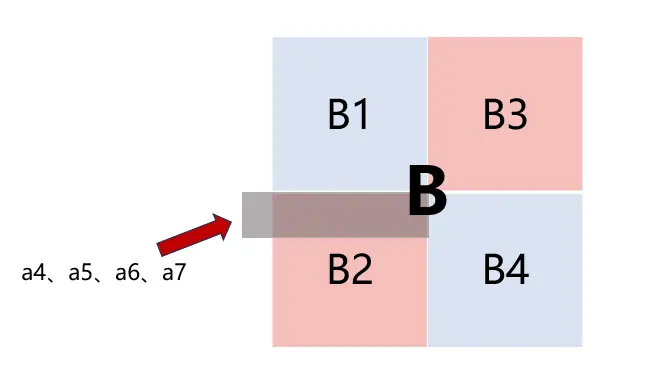
开始对B2进行处理。我们每次只对B2的一行进行处理，而这一行恰好将我们从B3中取出的一行驱逐掉，B3的这一行已经存放了对应的A3^T，并且B3这一行的数据被存放在局部变量中了，B2这一行对应的A2^T恰好存放在B3的这一行中，所以接下来，只需要将局部变量的值赋给B2这一行就好了，这样也将转置结果填入了B2这一行。循环操作，直至B1、B3都被驱逐，此时B2也填入了A2^T

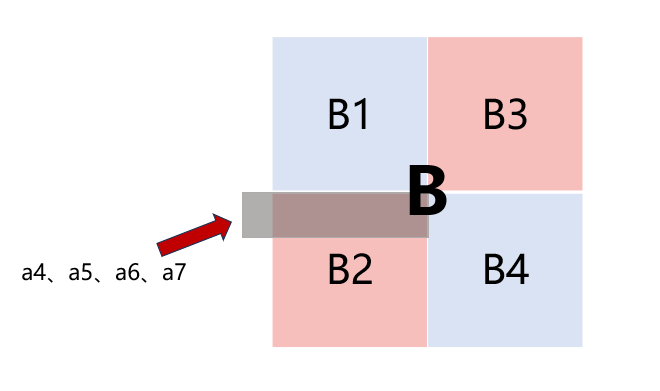
PS：这里有种思维惯性，就是总是想用A的一行转置到B的一列，但是形式所逼，只能用按行填入B3的转置结果，填入完一个行，才能放心地驱逐这一行

最后，很简单了，就是将A4^T填入到B4中，由于A4为4×4大小，而我们有8个局部变量可用，所以直接使用循环展开

代码

void transpose_submit(int M, int N, int A[N][M], int B[M][N]){ int a0, a1, a2, a3, a4, a5, a6, a7; for(int i=0; i<N; i+=8) { for(int j=0; j<M; j+=8) { //首先取出A1、A2，然后将它们转置到B1、B3 for(int k=i; k<i+4; ++k) { //读取A1 a0 = A[k][j+0]; a1 = A[k][j+1]; a2 = A[k][j+2]; a3 = A[k][j+3]; //读取A2 a4 = A[k][j+4]; a5 = A[k][j+5]; a6 = A[k][j+6]; a7 = A[k][j+7]; //将A1转置到B1 B[j+0][k] = a0; B[j+1][k] = a1; B[j+2][k] = a2; B[j+3][k] = a3; //将A2转置到B3 B[j+0][k+4] = a4; B[j+1][k+4] = a5; B[j+2][k+4] = a6; B[j+3][k+4] = a7; } //先用局部变量存放B3中一组的数据（设为B3中行a的数据），然后将A3的一列赋给B3的行a（给B3的这一组修改为A3的转置，没有miss），然后处理B2中的行b，其中，行b与B3中刚刚处理的行a有相同的组索引 //所以局部变量存放的正是B2中行b对应的A2转置，所以直接将局部变量存放的值赋给B2中的行b即可，而且由于驱逐的只有行a，所以这一步没有导致B3中其他数据丢失；由于行a与行b有相同的组索引，所以只有一次miss， //对应的是行b未命中，同时驱逐行a，而行a既将数据存放到局部变量，传给了行b（这是一个很好的性质，即行a与行b有相同的组索引，且行a与行b恰好在各自块中的行号相同，所以行b对应的A的转置存放在行a中） //又修改成了对应的A3转置，所以行a已经被处理好了，不需要再加载到缓存中进行处理，而行b也已经加载到缓存中了 for(int k=j; k<4+j; ++k) { //按行读取行a的数据，并存放到局部变量中 a4 = B[k][i+4]; a5 = B[k][i+5]; a6 = B[k][i+6]; a7 = B[k][i+7]; //将对应A3中的转置传给行a a0 = A[i+4][k]; a1 = A[i+5][k]; a2 = A[i+6][k]; a3 = A[i+7][k]; B[k][i+4] = a0; B[k][i+5] = a1; B[k][i+6] = a2; B[k][i+7] = a3; //处理B2中的行b，将局部变量a4~a7的值传给行b B[k+4][i+0] = a4; B[k+4][i+1] = a5; B[k+4][i+2] = a6; B[k+4][i+3] = a7; } //最后，处理B4，直接将A4转置，给B4，由于缓存中存在A2、A4，所以不会miss //由于有8个局部变量，而每个组中只有4个变量待处理，所以我利用循环展开，每两组进行处理 for(int k=i+4; k<i+8; k+=2) { a0 = A[k][j+4]; a1 = A[k][j+5]; a2 = A[k][j+6]; a3 = A[k][j+7]; a4 = A[k+1][j+4]; a5 = A[k+1][j+5]; a6 = A[k+1][j+6]; a7 = A[k+1][j+7]; B[j+4][k] = a0; B[j+5][k] = a1; B[j+6][k] = a2; B[j+7][k] = a3; B[j+4][k+1] = a4; B[j+5][k+1] = a5; B[j+6][k+1] = a6; B[j+7][k+1] = a7; } } }}

结果：

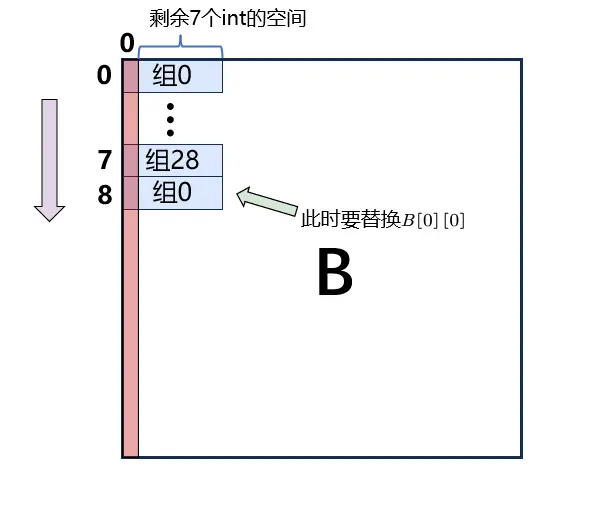
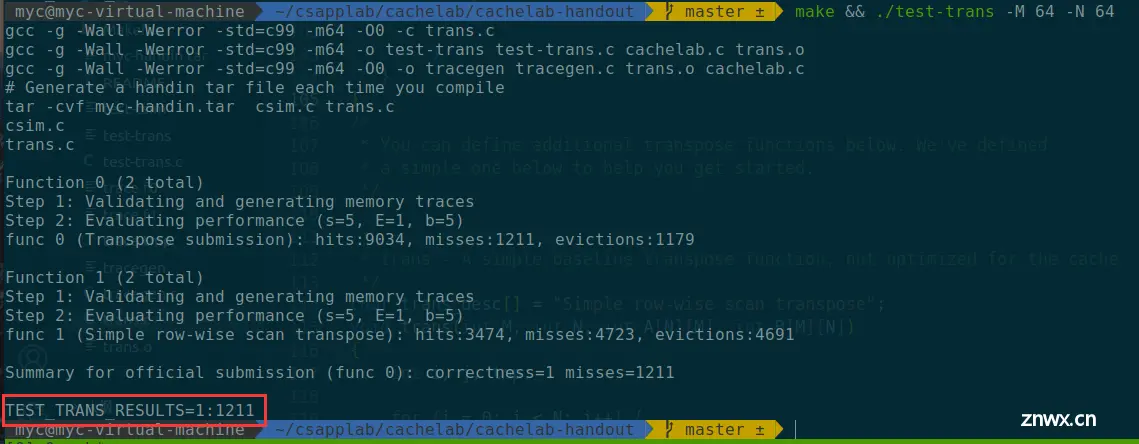
miss：1211，满分！

这个满分来之不易，真的很烧脑

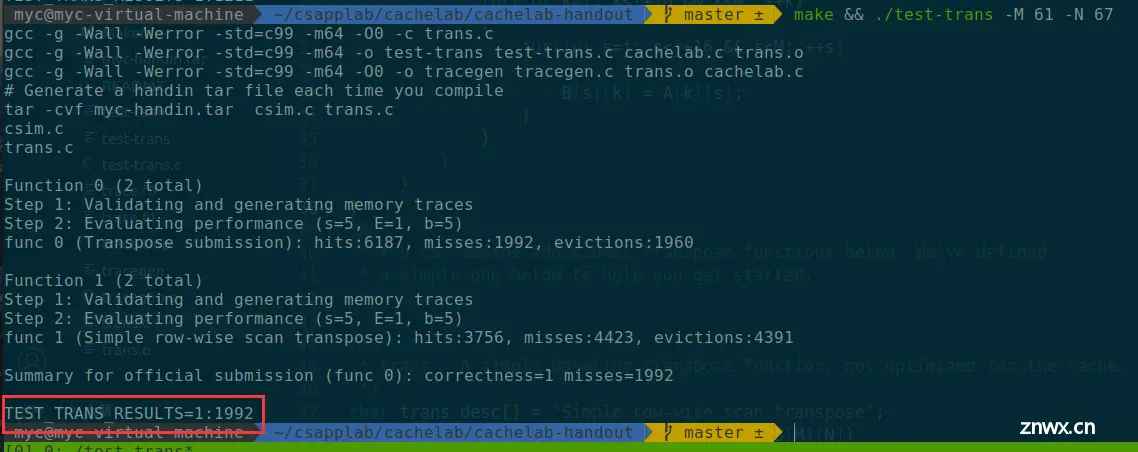
61×67

这个很宽松了，我尝试了几个分块方式，最终确定分为16×16

void transpose_submit(int M, int N, int A[N][M], int B[M][N]){ for (int i=0; i<N; i+=16) { for(int j=0; j<M; j+=16) { for(int k=i; k<i+16 && k<N; ++k) { for(int s=j; s<j+16 && s<M; ++s) { B[s][k] = A[k][s]; } } } }}

我看有的博客说17*17是miss最少的，不过16、17、18这几个分块方式都能满分，我也不过多研究了（做完64×64太累了）

结果：

擦线飘过

评分

满分53，Part A 27，Part B 26，代码风格7分由老师给

一个博主使用python3重构了driver.py：

wget https://gitee.com/lin-xi-269/csapplab/raw/master/lab5cachelab/cachelab-handout/driver.py

感谢作者：林夕丶，链接：(99+ 封私信 / 38 条消息) 林夕丶 - 知乎 (zhihu.com)

在下载之前，需要先将当前的driver.py删除，然后再用上面的下载指令，并将下载好的driver.py增加可执行权限

rm -rf driver.pywget https://gitee.com/lin-xi-269/csapplab/raw/master/lab5cachelab/cachelab-handout/driver.pychmod +x driver.py

然后就可以测试了

完整代码见github仓库：y-tanx/csapp: csapp lab,including solutions and explanations (github.com)

一些小感想：

优化的过程不是一蹴而就的，而是通过不断尝试，逐渐迭代优化，一点点靠近最优的方法，Part B中的64×64转置经历了4个版本的优化，通过不断尝试，分析性能瓶颈，找到了优化的方向，并在迭代优化中找到最优的方案Part A耗时有点长，我的代码能力需要多练了！Part B是个很有意思的实验，虽然转置的时间复杂度始终为O(n^2)，但是不同的转置方法对高速缓存的利用情况不同，最终导致性能有很大差别工具是用熟的，这次调试Part A的bug又用上了lab2时曾经用过的gdb工具，这次是彻底会用gdb来调试程序了；我学了一下git的使用，把我的代码上传到github中了，后面会陆续将前面实验的代码上传的github上这个实验涵盖了第6章的所有核心内容，做了这个lab，第六章又复习了一遍，对高速缓存的机制理解更透彻了，更加感觉高速缓存设计的巧妙，正如文章开头所言：“All problems in computer science can be solved by another level of indirection”，计算机领域中的所有问题都可以通过增加一个中间层来解决，存储器的层次结构正印证了这句话

本实验用时16h，两天；文章用时1天半写完