Attention Is All You Need——集中一下注意力

Transformer其实不是完全的Self-Attention（SA，自注意力）结构，还带有Cross-Attention（CA，交叉注意力）、残差连接、LayerNorm、类似1维卷积的Position-wise Feed-Forward Networks（FFN）、MLP和Positional Encoding（位置编码）等本文涵盖Transformer所采用的MHSA（多头自注意力）、LayerNorm、FFN、位置编码对1维卷积的详解请参考深入理解TDNN（Time Delay Neural Network）——兼谈x-vector网络结构对SA的Q、K、V运算的详解请参考深入理解Self-attention（自注意力机制）

Transformer的训练和推理

序列任务有三种： 序列转录：输入序列长度为N，输出序列长度为M，例如机器翻译序列标注：输入序列长度为N，输出序列长度也为N，例如词性标注序列总结：输入序列长度为N，输出为分类结果，例如声纹识别 前两个序列任务，常用Transformer进行统一建模，Transformer是一种Encoder-Decoder结构。在Transformer中：推理时 Encoder负责将输入 ( x 1 , x 2 , . . . , x n ) (x_1, x_2, ..., x_n) (x1​,x2​,...,xn​)，编码成隐藏单元（Hidden Unit） ( z 1 , z 2 , . . . , z n ) (z_1, z_2, ..., z_n) (z1​,z2​,...,zn​)，Decoder根据隐藏单元和过去时刻的输出 ( y 1 , y 2 , . . . , y t − 1 ) (y_{1}, y_{2}, ..., y_{t-1}) (y1​,y2​,...,yt−1​)， y 0 y_{0} y0​为起始符号"s"或者 y 0 = 0 y_{0}=0 y0​=0（很少见），解码出当前时刻的输出 y t y_{t} yt​，Decoder全部的输出表示为 ( y 1 , y 2 , . . . , y m ) (y_{1}, y_{2}, ..., y_{m}) (y1​,y2​,...,ym​)由于当前时刻的输出只依赖输入和过去时刻的输出（不包含未来信息），因此这种输出的生成方式是自回归式的，也叫因果推断（Causal Inference） 训练时 Encoder行为不变，Decoder根据隐藏单元和过去时刻的label ( y ^ 1 , y ^ 2 , . . . , y ^ t − 1 ) (\hat{y}_{1}, \hat{y}_{2}, ..., \hat{y}_{t-1}) (y^​1​,y^​2​,...,y^​t−1​)，解码出当前时刻的输出 y t y_{t} yt​，由于需要对每个 y t y_{t} yt​计算损失，而系统必须是因果的，因此每次解码时，需要Mask掉未来的信息，也就是全部置为 − ∞ -\infty −∞（从而Softmax运算后接近0），当label为“s I am a student”，则Decoder每一时刻的输入，如下图

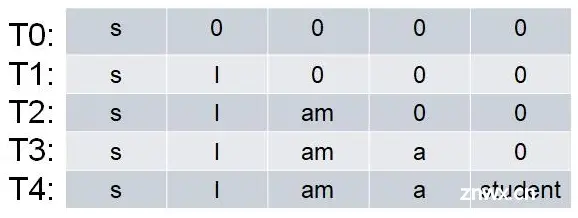
这种将label作为Decoder的输入的训练方式叫做Teacher Forcing，类似上述推理时将输出作为Decoder的输入的训练方式叫做Free Running。Teacher Forcing允许并行计算出每个时刻的输出，因此是最常用的

Transformer的Encoder和Decoder

Transformer的Encoder行为与上述一致，设Encoder的输入特征图形状为 ( n , d m o d e l ) (n, d_{model}) (n,dmodel​)，即长度为n的序列，序列的每个元素是 d m o d e l d_{model} dmodel​维的向量，Encoder Layer（如下图左边重复N次的结构）是不改变输入特征图形状的，并且Encoder Layer内部的Sub-layer也是不改变输入特征图形状的，从而Encoder的输出特征图形状也为 ( n , d m o d e l ) (n, d_{model}) (n,dmodel​)这样设计的原因是：每个Encoder Layer都有两次残差连接（如下图中的Add运算），残差连接要求输入输出特征图形状不变，为了减少超参数，所以这样设计

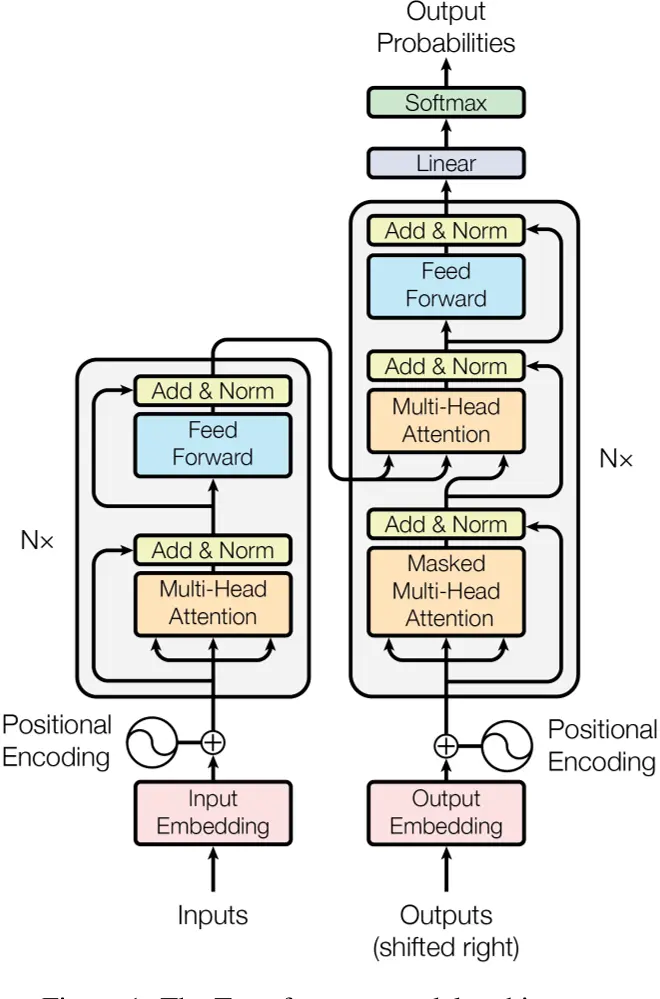
LayerNorm

LayerNorm（如上图中的Norm运算）常用在可变长度序列任务里，接下来通过对比BatchNorm和LayerNorm，认识LayerNorm

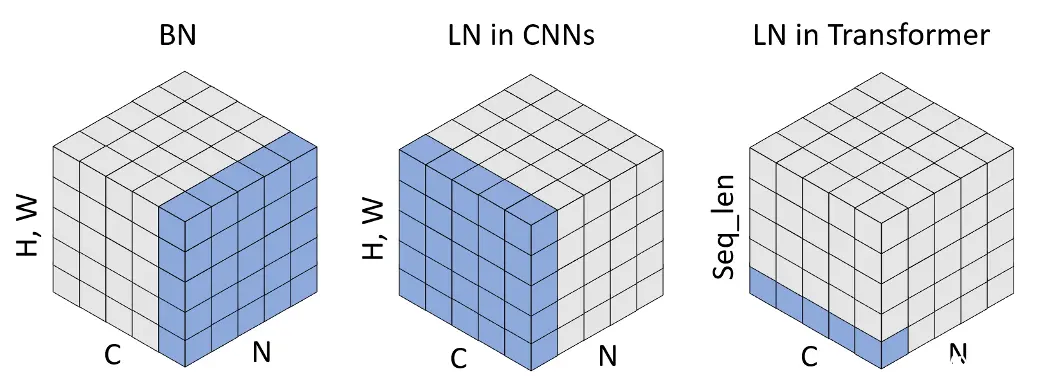
左图为BN，C为单个样本的特征维度（即特征图的Channels，表示特征的数量），H、W为特征的形状，因为特征可以是矩阵也可以是向量，因此统称特征形状。BN希望将每个特征变成0均值1方差，再变换成新的均值和方差，因此需要在一个Batch中，找寻每个样本的该特征，然后计算该特征的统计量，由于每个特征的统计量需要单独维护，因此构造BN需要传入特征的数量，也就是C。同时，BN的可学习参数 w e i g h t + b i a s = 2 ∗ C weight+bias=2*C weight+bias=2∗C中图为LN，LN希望不依赖Batch，将单个样本的所有特征变成0均值1方差，再变换成新的均值和方差，因此需要指定样本形状，告诉LN如何计算统计量，由于样本中的每个值，都进行均值和方差的变换，因此构造LN需要传入样本的形状，也就是C、H、W。同时，LN的可学习参数 w e i g h t + b i a s = 2 ∗ C ∗ H ∗ W weight+bias=2*C*H*W weight+bias=2∗C∗H∗W示例：

>>> input=torch.rand([1, 3, 2, 2])>>> inputtensor([[[[0.1181, 0.6704], [0.7010, 0.8031]], [[0.0630, 0.2088], [0.2150, 0.6469]], [[0.5746, 0.4949], [0.3656, 0.7391]]]])>>> layer_norm=torch.nn.LayerNorm((3, 2, 2), eps=1e-05)>>> output=layer_norm(input)>>> outputtensor([[[[-1.3912, 0.8131], [ 0.9349, 1.3424]], [[-1.6113, -1.0293], [-1.0047, 0.7191]], [[ 0.4308, 0.1126], [-0.4035, 1.0872]]]], grad_fn=<NativeLayerNormBackward0>)>>> output[0].mean()tensor(-1.7385e-07, grad_fn=<MeanBackward0>)>>> output[0].std()tensor(1.0445, grad_fn=<StdBackward0>)>>> layer_norm.weight.shapetorch.Size([3, 2, 2])>>> layer_norm.bias.shapetorch.Size([3, 2, 2])# 等价于>>> mean=input.mean(dim=(-1, -2, -3), keepdim=True)>>> var=input.var(dim=(-1, -2, -3), keepdim=True, unbiased=False)>>> (input-mean)/torch.sqrt(var+1e-05)tensor([[[[-1.3912, 0.8131], [ 0.9349, 1.3424]], [[-1.6113, -1.0293], [-1.0047, 0.7191]], [[ 0.4308, 0.1126], [-0.4035, 1.0872]]]]) 上述两种情况为计算机视觉中的BN和LN，可以看出，BN训练时需要更新统计量，从而推理时使用统计量进行Norm，而LN训练和推理时的行为是一致的在序列任务中，特征形状为1，多出来一个序列长度Seq_len，其他不变，1维的BN（BatchNorm1d）在N*Seq_len个帧中，计算每个特征的统计量，从而序列任务中的帧形状是C，因此LN要传入的帧形状是C，并且Input的形状中，C这个维度要放在最后1维的BN常用于声纹识别，但是Transformer风格的模型基本都采用LN，并且LN是适用于任何特征形状的，BN则根据特征形状不同，衍生出BatchNorm1d、BatchNorm2d等示例

>>> input=torch.rand([1, 200, 80])>>> layer_norm=torch.nn.LayerNorm(80)>>> layer_norm(input)[0][0].mean()tensor(8.3447e-08, grad_fn=<MeanBackward0>)>>> layer_norm(input)[0][1].mean()tensor(-8.0466e-08, grad_fn=<MeanBackward0>)>>> layer_norm(input)[0][0].std()tensor(1.0063, grad_fn=<StdBackward0>)>>> layer_norm(input)[0][1].std()tensor(1.0063, grad_fn=<StdBackward0>) 在序列任务中采用LN而不是BN的原因 序列任务的样本很多时候是不等长的，很多时候要补0帧，当batch-size较小时，BN的统计量波动较大，而LN是对每一帧进行Norm的，不受补0帧的影响训练时要构造一个Batch，因此序列长度只能固定，但是推理时序列长度是可变的，采用BN容易过拟合序列长度，LN则不容易过拟合序列长度

SA（自注意力）与CA（交叉注意力）

对于一个输入序列 ( seq-len , d m o d e l ) (\text{seq-len}, d_{model}) (seq-len,dmodel​)，SA通过Q、K、V计算矩阵，计算得到对应长度的Q、K、V序列，这些序列构成Q、K、V矩阵如果Q、K、V矩阵完全由同一个序列计算而来，则称为自注意力SA；如果V、K矩阵由同一个序列计算而来，Q矩阵由另一个序列计算而来，则称为交叉注意力CA需要注意，Decoder Layer中的第二个MHSA（如下图），从左到右的输入，计算顺序是V、K、Q，其中V、K是根据输入的隐藏单元进行计算的，即 ( z 1 , z 2 , . . . , z n ) (z_1, z_2, ..., z_n) (z1​,z2​,...,zn​)，得到的V、K矩阵形状分别为 ( n , d k ) (n, d_k) (n,dk​)、 ( n , d v ) (n, d_v) (n,dv​)，而Q是根据输出的隐藏单元进行计算的，即 ( z ^ 1 , z ^ 2 , . . . , z ^ m ) (\hat{z}_1, \hat{z}_2, ..., \hat{z}_m) (z^1​,z^2​,...,z^m​)，得到的Q矩阵形状为 ( m , d k ) (m, d_k) (m,dk​)，因此这是一种CA运算

SA和CA的后续运算是一致的，V、K、Q矩阵通过Attention函数计算Attention分数，然后对V矩阵进行加权求和，得到Attention的输出。Transformer用的Attention函数是Scaled Dot-Product Attention，公式如下：

Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text{Attention}(Q, K, V)=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dk​ ​QKT​)V如果是Decoder的Attention函数则需要Mask掉softmax的输出，使得未来时刻对应的V接近0，如下图：

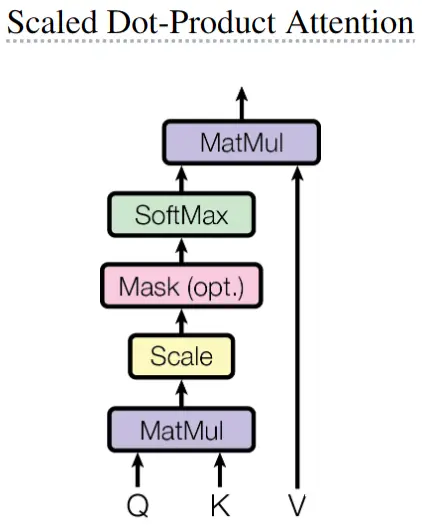
计算的细化过程如下图：

Q K T QK^T QKT内积的含义是计算相似度，因此中间 ( m , n ) (m, n) (m,n)矩阵的第m行，表示第m个query对所有key的相似度之后除以 d k \sqrt{d_k} dk​ ​进行Scale，并且Mask（具体操作为将未来时刻对应的点积结果置为 − ∞ -\infty −∞，从而Softmax运算后接近0），然后对 ( m , n ) (m, n) (m,n)矩阵的每一行进行Softmax最后output矩阵的第m行，表示第m个权重对不同帧的value进行加权求和需要注意的是 Attention最后的输出，序列长度由Q决定，向量维度由V决定Q和K的向量维度一致，序列长度可以不同；K和V的序列长度一致，向量维度可以不同Softmax是在计算第m个query对不同key的相似度的权重，求和为1除以 d k \sqrt{d_k} dk​ ​的原因是因为后面需要进行Softmax运算，具有最大值主导效果。当 d k d_k dk​较小时，点积的结果差异不大，当 d k d_k dk​较大时，点积的结果波动较大（假设每个query和key都是0均值1方差的多维随机变量，则它们的点积 q ⋅ k = ∑ i = 1 d k q i k i q \cdot k=\sum_{i=1}^{d_k} q_ik_i q⋅k=∑i=1dk​​qi​ki​，为0均值 d k d_k dk​方差的多维随机变量），从而Softmax后，大量值接近0，这样会导致梯度变得很小，不利于收敛。因此除以一个值，会使得这些点积结果的值变小，从而Softmax运算的最大值主导效果不明显

MHSA

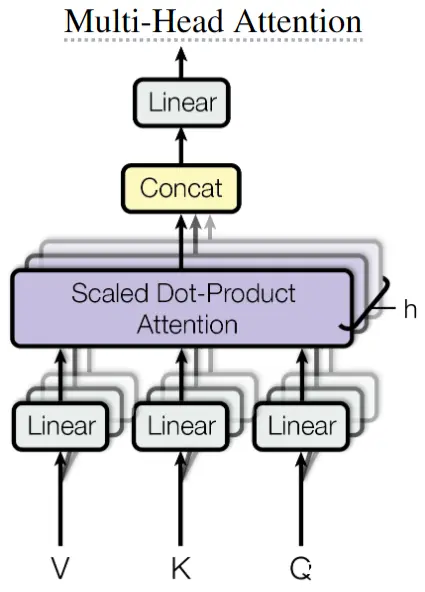
多头注意力的动机是：与其将输入投影到较高的维度，计算单个注意力，不如将输入投影到h个较低的维度，计算h个注意力，然后将h个注意力的输出在特征维度Concat起来，最后利用MLP进行多头特征聚合，得到MHSA的输出。MHSA的公式如下：

MultiHead ( Q , K , V ) = Concat ( h e a d 1 , h e a d 2 , . . . , h e a d h ) W O h e a d i = Attention ( Q i , K i , V i ) \begin{aligned} \text{MultiHead}(Q, K, V)&=\text{Concat}(head_1, head_2, ..., head_h)W^O \\ head_i&=\text{Attention}(Q_i, K_i, V_i) \end{aligned} MultiHead(Q,K,V)headi​​=Concat(head1​,head2​,...,headh​)WO=Attention(Qi​,Ki​,Vi​)​由于MHSA不能改变输入输出形状，所以每个SA的设计是：当 d m o d e l = 512 d_{model}=512 dmodel​=512， h = 8 h=8 h=8时， d k = d v = d m o d e l / h = 64 d_k=d_v=d_{model}/h=64 dk​=dv​=dmodel​/h=64在实际运算时，可以通过一个大的矩阵运算，将输入投影到 ( n , d m o d e l ) (n, d_{model}) (n,dmodel​)，然后在特征维度Split成h个矩阵，Q、K、V都可如此操作因此一个MHSA的参数量： 4 ∗ d m o d e l ∗ d m o d e l = 4 ∗ d m o d e l 2 4*d_{model}*d_{model}=4*d^2_{model} 4∗dmodel​∗dmodel​=4∗dmodel2​，即Q、K、V加最后的MLP

FFN

FFN的操作和MHSA中最后的MLP非常相似的，公式和图如下：

FFN ( x ) = m a x ( 0 , x W 1 + b 1 ) W 2 + b 2 \text{FFN}(x)=max(0,xW_1+b_1)W_2+b_2 FFN(x)=max(0,xW1​+b1​)W2​+b2​

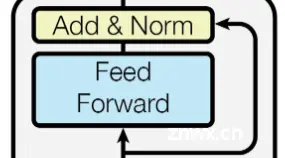
采用同一个MLP，对输入特征的每一帧进行维度变换（通常是增大为4倍），然后RELU，最后再采用另一个MLP，将输入特征的每一帧恢复回原来的维度因此一个FFN的参数量： d m o d e l ∗ 4 ∗ d m o d e l + 4 ∗ d m o d e l ∗ d m o d e l = 8 ∗ d m o d e l 2 d_{model}*4*d_{model}+4*d_{model}*d_{model}=8*d^2_{model} dmodel​∗4∗dmodel​+4∗dmodel​∗dmodel​=8∗dmodel2​，即维度提升MLP加维度恢复MLP综合，一个Encoder Layer的参数量为： 12 ∗ d m o d e l 2 12*d^2_{model} 12∗dmodel2​，一个Decoder Layer的参数量为： 16 ∗ d m o d e l 2 16*d^2_{model} 16∗dmodel2​上述所有参数估计忽略LayerNorm的参数，因为其数量级较小

Embedding Layer和Softmax

Encoder和Decoder的Embedding Layer，以及最后的Softmax输出前，都有一个MLP，在Transformer中，这三个MLP是共享参数的，形状都是 ( dict-len , d m o d e l ) (\text{dict-len}, d_{model}) (dict-len,dmodel​)， dict-len \text{dict-len} dict-len是字典大小在Embedding Layer中，权重都被除以了 d m o d e l \sqrt{d_{model}} dmodel​ ​，从而Embedding的输出范围在[-1, 1]附近，这是为了让Embedding的值范围靠近Positional Encoding，从而可以直接相加

Positional Encoding（位置编码）

Attention的输出是不具有时序信息的，如果把输入打乱，那么也只会导致对应的输出打乱而已，不会有导致值变化，但序列任务往往关注时序信息，一件事先发生和后发生，意义是不一样的，因此需要对Attention的输入添加位置编码位置编码的公式如下：

PE ( p o s , 2 i ) = s i n ( p o s / 1000 0 2 i d m o d e l ) PE ( p o s , 2 i + 1 ) = c o s ( p o s / 1000 0 2 i d m o d e l ) \begin{aligned} \text{PE}(pos, 2i)=sin(pos/10000^{\frac{2i}{d_{model}}}) \\ \text{PE}(pos, 2i+1)=cos(pos/10000^{\frac{2i}{d_{model}}}) \end{aligned} PE(pos,2i)=sin(pos/10000dmodel​2i​)PE(pos,2i+1)=cos(pos/10000dmodel​2i​)​pos表示帧的位置，第二个参数表示特征的位置，奇偶交替，也就说：不同位置的同一特征，根据位置映射不同频率的正弦函数进行编码；同一位置的不同特征，根据奇偶分布映射不同频率的正弦函数进行编码位置编码值的范围是[-1, 1]（Embedding的权重需要除以 d m o d e l \sqrt{d_{model}} dmodel​ ​的原因），与Embedding对应元素相加，即可输入到Attention中