一、功能

直方图是一种将数据分组到条柱中的条形图。该函数可以统计数据在划分区间内的数量分布，同时以直方图的形式展示统计结果。

二、语法

1、histogram（X）

创建直方图X的图。该函数使用 一种自动分箱算法，返回具有统一宽度的分箱， 选择以涵盖元素范围并揭示 分布的基础形状。 将条柱显示为矩形条，以便每个矩形的高度 表示箱中的元素数。

2、histogram（X，nbins）

指定条柱的数量。

3、histogram（X，edges）

将条柱边分类到X向量。

4、histogram（'BinEdges'，edges，'BinCounts'，counts）

绘制指定的条柱计数，并且不执行任何数据条箱。

5、histogram（C，Categories）

仅绘制C中的类别子集。

6、histogram（'Categories'，Categories，'BinCounts'，counts）

手动指定类别和关联的 bin 计数。 绘制指定的条柱计数并执行histogram不执行任何数据合并。

7、输入数据

X— 要在 bin 向量之间分配的数据

C— 分类数据

nbins— 条柱数，正整数

edges— 条柱边，向量

Categories— 字符向量的直方图 元胞数组中包含的类别

counts— Bin 计数

三、示例

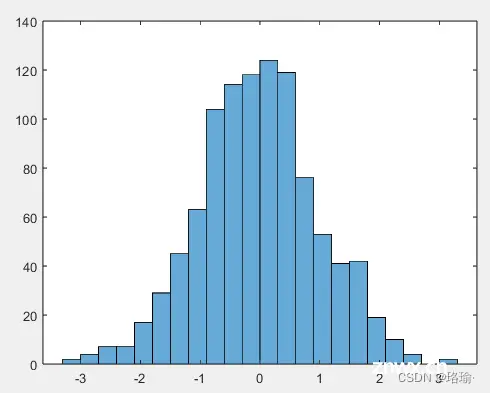
1、向量直方图

生成 10,000 个随机数并创建直方图。该函数会自动选择适当数量的条柱，以覆盖值范围并显示基础分布的形状。

<code>x = randn(10000,1);

h = histogram(x)

2、指定直方图条柱数

绘制 1,000 个随机数的直方图，这些随机数被分类到 25 个等距的条柱中。

<code>x = randn(1000,1);

nbins = 25;

h = histogram(x,nbins)

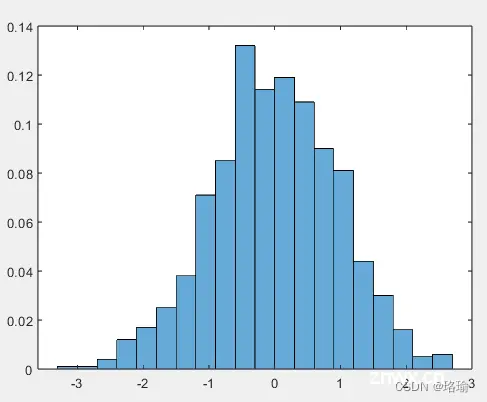
3、更改直方图条柱的数量

生成 1,000 个随机数并创建直方图。

<code>X = randn(1000,1);

h = histogram(X)

使用该功能粗略调整箱数。

<code>Nbins = morebins(h)

通过显式设置条柱数量，在细粒度级别调整条柱。

<code>h.NumBins = 31;

4、指定直方图的条柱边

生成 1,000 个随机数并创建直方图。将条柱边指定为在直方图边上具有宽条柱的向量，以捕获不满足条件的异常值∣x∣<2.第一个向量元素是第一个条柱的左边缘，最后一个向量元素是最后一个条柱的右边缘。

<code>x = randn(1000,1);

edges = [-10 -2:0.25:2 10];

h = histogram(x,edges);

指定属性以展平包含异常值的条柱。现在，每个条柱的面积（而不是高度）表示该区间内的观测频率。

<code>h.Normalization = 'countdensity';

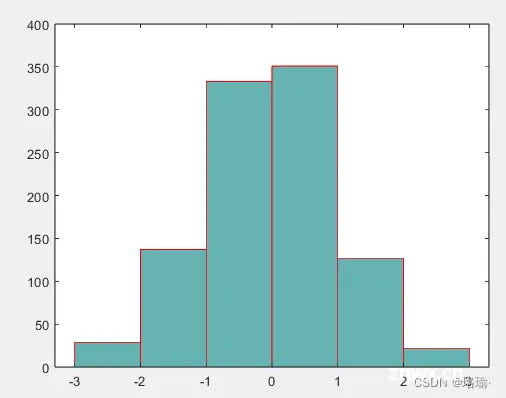
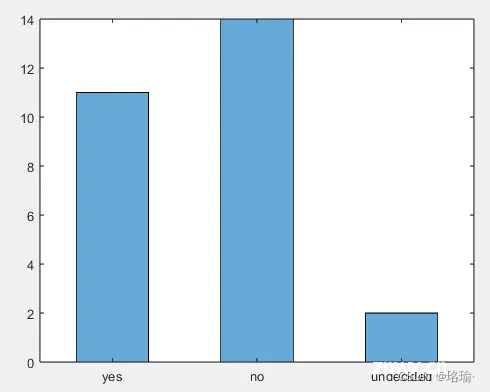
5、绘制分类直方图

创建表示投票的分类向量。向量中的类别为 、 或 。<code>'yes''no''undecided'

A = [0 0 1 1 1 0 0 0 0 NaN NaN 1 0 0 0 1 0 1 0 1 0 0 0 1 1 1 1];

C = categorical(A,[1 0 NaN],{'yes','no','undecided'})

绘制投票的分类直方图，使用相对柱形宽度 0.5。

h = histogram(C,'BarWidth',0.5)

6、具有指定归一化的直方图

生成 1,000 个随机数并使用归一化创建直方图。

<code>x = randn(1000,1);

h = histogram(x,'Normalization','probability')

计算条形高度的总和。通过此归一化，每个条形的高度等于在该条柱间隔内选择观测值的概率，并且所有条形的高度总和为 1。

<code>S = sum(h.Values)

7、使用百分比的直方图

生成 100,000 个正态分布的随机数。使用标准差 15 和平均值 100。

x = 100 + 15*randn(1e5,1);

绘制随机数的直方图。缩放 y 轴并将其标记为百分比。

edges = 55:15:145;

histogram(x,edges,Normalization="percentage")code>

ytickformat("percentage")

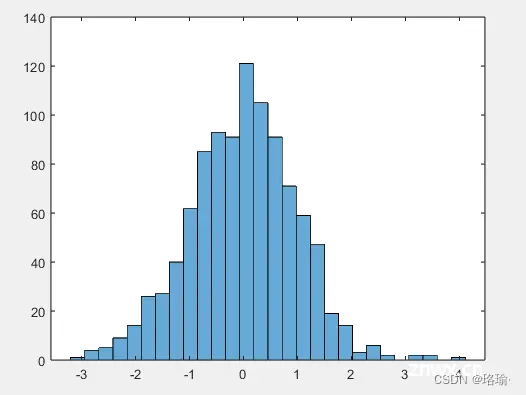
8、绘制多个直方图

<code>x = randn(2000,1);

y = 1 + randn(5000,1);

h1 = histogram(x);

hold on

h2 = histogram(y);

由于直方图的样本大小和条柱宽度不同，因此很难进行比较。对直方图进行归一化，使所有条形高度相加为 1，并使用统一的条柱宽度。

<code>h1.Normalization = 'probability';

h1.BinWidth = 0.25;

h2.Normalization = 'probability';

h2.BinWidth = 0.25;

9、调整直方图属性

生成 1,000 个随机数并创建直方图。返回直方图对象以调整直方图的属性，而无需重新创建整个绘图。

<code>x = randn(1000,1);

h = histogram(x)

准确指定要使用的箱数。

<code>h.NumBins = 15;

使用矢量指定条柱的边缘。向量中的第一个值是第一个条柱的左边缘。最后一个值是最后一个条柱的右边缘。

<code>h.BinEdges = [-3:3];

更改直方图条的颜色。

<code>h.FaceColor = [0 0.5 0.5];

h.EdgeColor = 'r';

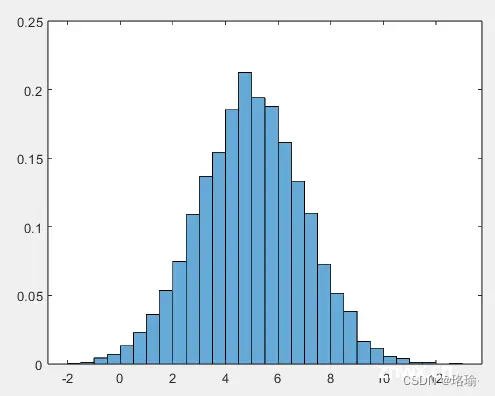
10、确定基础概率分布

生成 5,000 个正态分布的随机数，平均值为 5，标准差为 2。绘制直方图以生成概率密度函数的估计值。

<code>x = 2*randn(5000,1) + 5;

histogram(x,'Normalization','pdf')

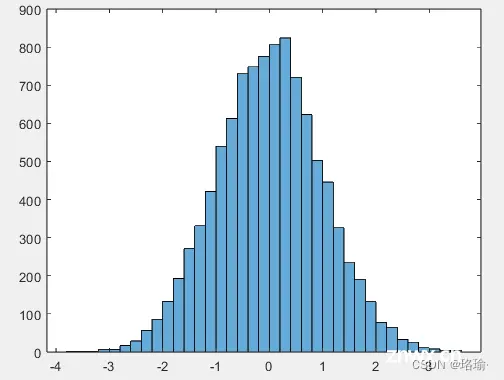
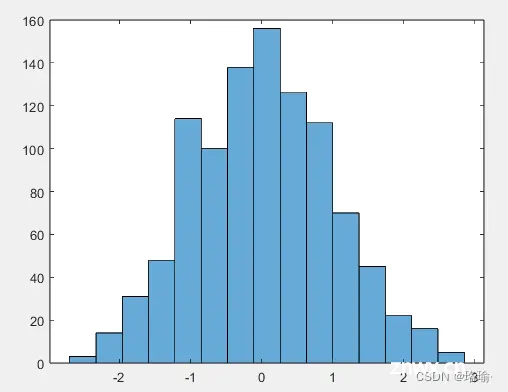
在此示例中，正态分布数据的基础分布是已知的。但是，您可以使用直方图，通过将数据与已知概率密度函数进行比较，来确定数据的基础概率分布pdf。

均值为正态分布的概率密度函数μ标准差σ和方差σ2是

叠加均值为 5 且标准差为 2 的正态分布的概率密度函数图。

<code>hold on

y = -5:0.1:15;

mu = 5;

sigma = 2;

f = exp(-(y-mu).^2./(2*sigma^2))./(sigma*sqrt(2*pi));

plot(y,f,'LineWidth',1.5)

11、保存和加载直方图对象

使用该功能保存图窗。

<code>histogram(randn(10));

savefig('histogram.fig');

close gcf

用于将直方图加载回 MATLAB®。 还返回图的句柄。

h = openfig('histogram.fig');

使用该函数从图窗手柄中找到正确的对象手柄。这允许您继续操作用于生成图窗的原始直方图对象。

<code>y = findobj(h,'type','histogram')