C++从入门到起飞之——红黑树 全方位剖析!
秋风起,再归来~ 2024-10-27 09:35:01 阅读 54

🌈个人主页:秋风起,再归来~
🔥系列专栏:C++从入门到起飞
🔖克心守己,律己则安
目录
1. 红⿊树的概念
2. 红⿊树的实现
2.1 构建整体框架
2.2 红黑树的插入
2.3 红黑树的验证
2.4 红黑树的其他简单接口
3、红黑树完整源码
4、完结散花
1. 红⿊树的概念
红⿊树是⼀棵⼆叉搜索树,他的每个结点增加⼀个存储位来表⽰结点的颜⾊,可以是红⾊或者⿊⾊。 通过对任何⼀条从根到叶⼦的路径上各个结点的颜⾊进⾏约束,红⿊树确保没有⼀条路径会⽐其他路 径⻓出2倍,因⽽是接近平衡的。
>红⿊树的规则:
1. 每个结点不是红⾊就是⿊⾊
2. 根结点是⿊⾊的
3. 如果⼀个结点是红⾊的,则它的两个孩⼦结点必须是⿊⾊的,也就是说任意⼀条路径不会有连续的 红⾊结点。
4. 对于任意⼀个结点,从该结点到其所有NULL结点的简单路径上,均包含相同数量的⿊⾊结点
说明:《算法导论》等书籍上补充了⼀条每个叶⼦结点(NIL)都是⿊⾊的规则。他这⾥所指的叶⼦结点 不是传统的意义上的叶⼦结点,⽽是我们说的空结点,有些书籍上也把NIL叫做外部结点。NIL是为了 ⽅便准确的标识出所有路径,《算法导论》在后续讲解实现的细节中也忽略了NIL结点,所以我们知道 ⼀下这个概念即可。

2. 红⿊树的实现
2.1 构建整体框架
枚举类型定义红黑色:
<code>//枚举类型定义颜色
enum Colour
{
RED,
BLACK
};
红黑树每个节点的结构:
//节点结构(默认存储pair类型的key/val结构)
template<class K, class V>
struct RBTreeNode
{
RBTreeNode(const pair<K, V>& kv)
:_kv(kv)
, _parent(nullptr)
, _left(nullptr)
, _right(nullptr)
,_col(RED)
{}
pair<K, V> _kv;
RBTreeNode* _parent;
RBTreeNode* _left;
RBTreeNode* _right;
Colour _col;//初始化为红色
};
红黑树整体结构
//红黑树
template<class K,class V>
class RBTree
{
typedef RBTreeNode Node;
public:
//各种接口的实现
private:
Node* _root=nullptr;
};
2.2 红黑树的插入
1、红黑树是特殊的二叉搜索数,所以我们进行插入时,还是先按照二叉搜索数的规则进行插入!
//如果树为空,在根插入并且颜色为黑色
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
//树不为空按搜索树规则先进行插入
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (kv.first < cur->_kv.first)//小往左走
{
parent = cur;
cur = parent->_left;
}
else if (kv.first > cur->_kv.first)//大往右走
{
parent = cur;
cur = parent->_right;
}
else
{
return false;//不支持相同元素的插入
}
}
cur = new Node(kv);
cur->_col = RED;
if (kv.first < parent->_kv.first)//K小插入在左边
parent->_left = cur;
else//K大插入在右边
parent->_right = cur;
cur->_parent = parent;
2、插入成功后,我们就要维护红黑树的规则了。
>如果插入节点的父亲是黑色,那插入后依然符合红黑树的规则,我们不用处理。
>如果插入节点的父亲是红色,那么此时就有连续的红色节点,我们就要进行处理。
a、插入节点的叔叔存在且为红,我们只需要进行变色。

变色原理:因为parent的颜色为红,所以g的颜色一定为黑。插入前从g开始的路径的黑色节点的数量相同,要解决连续红色节点的问题,我们必然要把parent变黑色。但从g到cur路径的黑色节点多了一个,所以我们把g变红,在把u变黑就完美的解决了问题!

不过,g变红后,又可能会引起祖先节点的连续红色节点问题,所以我们还要继续向上维护红黑树的规则!
变色代码实现
<code>//插入后进行维护红黑树规则的逻辑
//parent存在且为红
while (parent&& parent->_col = RED)
{
Node* grandfather = parent->_parent;
//p在g的右边
if (parent == grandfather->_right)
{
//g
//up
Node* uncle = grandfather->_left;
if (uncle&& uncle->_col = RED)//uncle存在且为红
{
//变色处理
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
//更新cur继续向上处理
cur = grandfather;
parent = cur->_parent;
}
else//uncle不存在或者存在且为黑
{
}
}
else//p在g的左边
{
//g
//pu
Node* uncle = grandfather->_left;
if (uncle&& uncle->_col = RED)//uncle存在且为红
{
//变色处理
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
//更新cur继续向上处理
cur = grandfather;
parent = cur->_parent;
}
else//uncle不存在或者存在且为黑
{
}
}
}
b、如果uncle不存在或者uncle存在且为黑,这时我们就要进行旋转加变色处理。
单旋+变色:
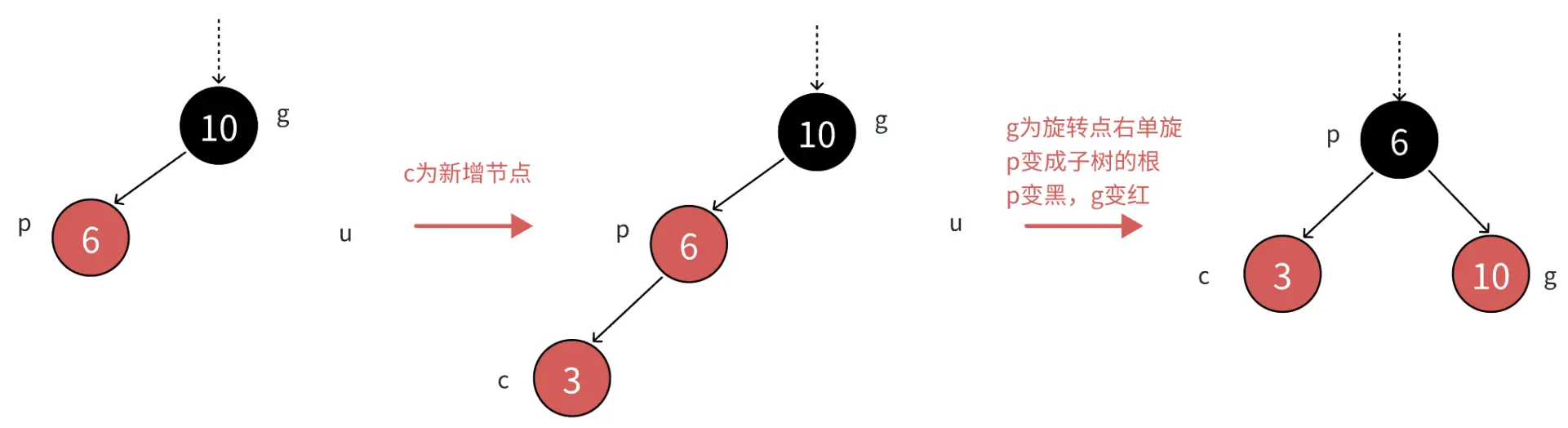
>如果uncle不存在,说明c一定是新增节点,如果c是变色后的节点,那么它在变色前一定是黑色,而从g开始的路径到c就多一个黑色节点!
>如果uncle存在且为黑,说明c一定是变色后的节点,如果c是新增的节点,那么从g开始的路径到u就多一个黑色节点!
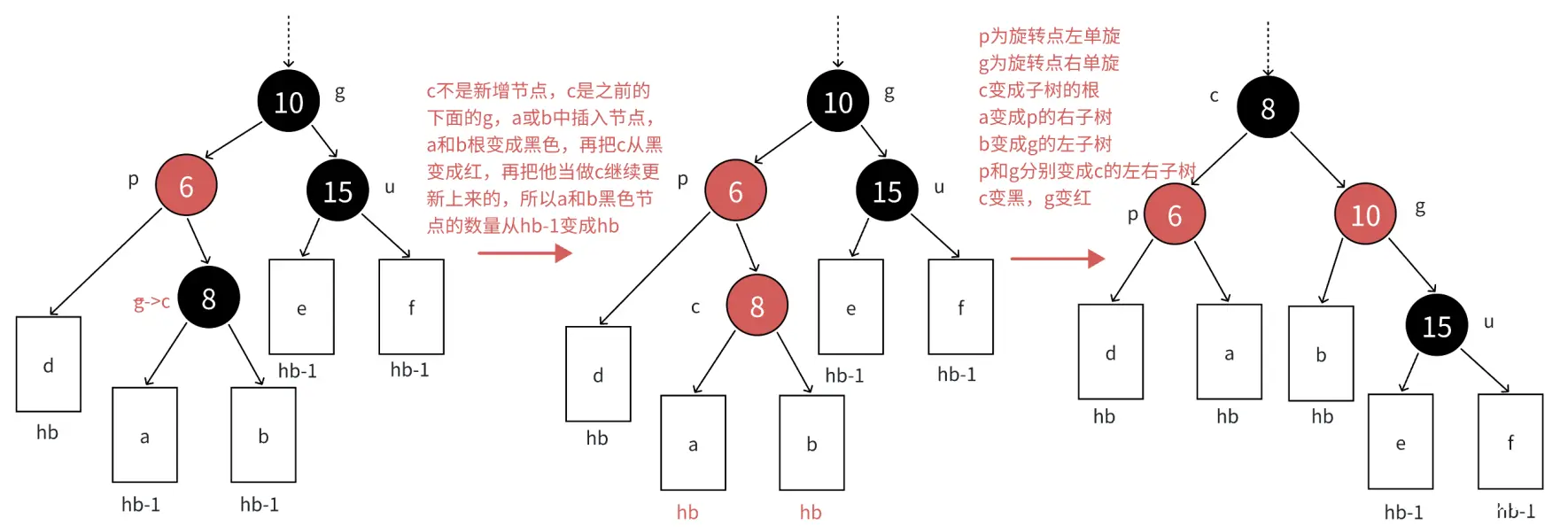
变色原理:我们根据c、p、g的位置来选择合理的旋转逻辑,然后再把p变黑,g变红即可解决问题!
双旋+变色:
c为红,p为红,g为⿊,u不存在或者u存在且为⿊,u不存在,则c⼀定是新增结点,u存在且为⿊,则 c⼀定不是新增,c之前是⿊⾊的,是在c的⼦树中插⼊,符合情况1,变⾊将c从⿊⾊变成红⾊,更新上 来的。
分析:p必须变⿊,才能解决,连续红⾊结点的问题,u不存在或者是⿊⾊的,这⾥单纯的变⾊⽆法解 决问题,需要旋转+变⾊。
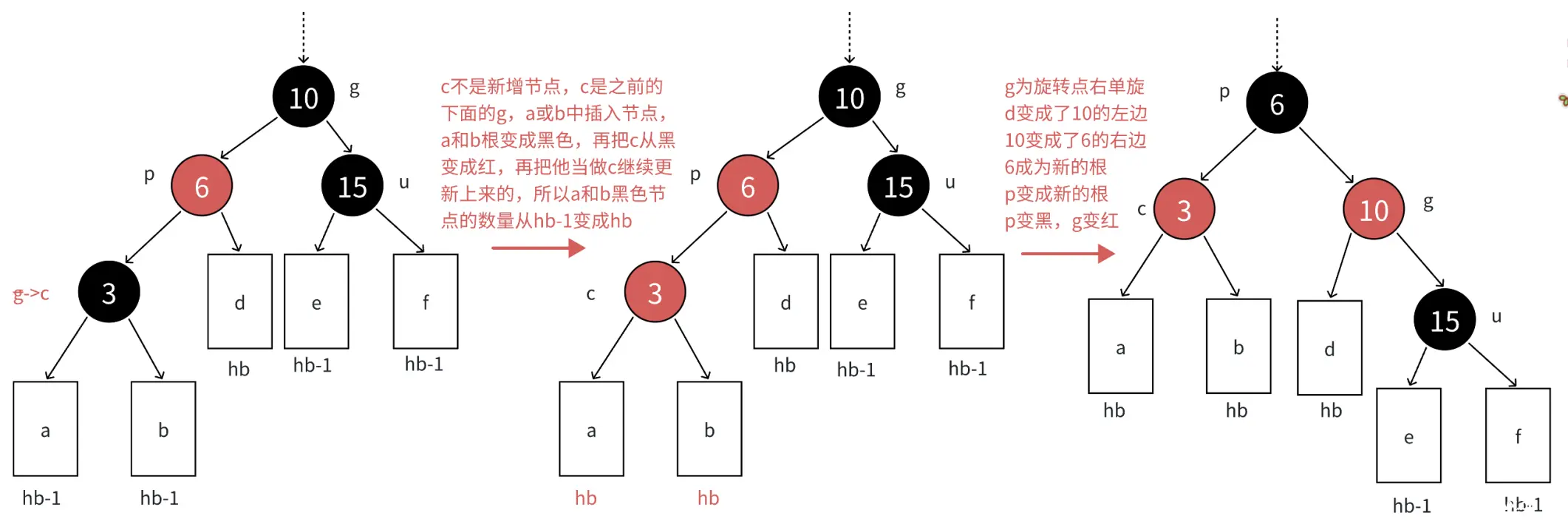
如果p是g的左,c是p的右,那么先以p为旋转点进⾏左单旋,再以g为旋转点进⾏右单旋,再把c变 ⿊,g变红即可。c变成课这颗树新的根,这样⼦树⿊⾊结点的数量不变,没有连续的红⾊结点了,且 不需要往上更新,因为c的⽗亲是⿊⾊还是红⾊或者空都不违反规则。
如果p是g的右,c是p的左,那么先以p为旋转点进⾏右单旋,再以g为旋转点进⾏左单旋,再把c变 ⿊,g变红即可。c变成课这颗树新的根,这样⼦树⿊⾊结点的数量不变,没有连续的红⾊结点了,且 不需要往上更新,因为c的⽗亲是⿊⾊还是红⾊或者空都不违反规则。

插入完整代码:
<code>bool insert(const pair<K, V>& kv)
{
//如果树为空,在根插入并且颜色为黑色
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
//树不为空按搜索树规则先进行插入
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (kv.first < cur->_kv.first)//小往左走
{
parent = cur;
cur = parent->_left;
}
else if (kv.first > cur->_kv.first)//大往右走
{
parent = cur;
cur = parent->_right;
}
else
{
return false;//不支持相同元素的插入
}
}
cur = new Node(kv);
cur->_col = RED;
if (kv.first < parent->_kv.first)//K小插入在左边
parent->_left = cur;
else//K大插入在右边
parent->_right = cur;
cur->_parent = parent;
//插入后进行维护红黑树规则的逻辑
//parent存在且为红
while (parent&& parent->_col == RED)
{
Node* grandfather = parent->_parent;
//p在g的右边
if (parent == grandfather->_right)
{
//g
//up
Node* uncle = grandfather->_left;
if (uncle&& uncle->_col == RED)//uncle存在且为红
{
//变色处理
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
//更新cur继续向上处理
cur = grandfather;
parent = cur->_parent;
}
else//uncle不存在或者存在且为黑
{
if (cur == parent->_right)
{
//g
//up
// c
//以g为旋转点进行左单旋
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
//g
//up
// c
//进行右左双旋
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
//旋转+变色后链接祖先节点的节点为黑,必然不会发生连续红色节点的情况直接break;
break;
}
}
else//p在g的左边
{
//g
//pu
Node* uncle = grandfather->_left;
if (uncle&& uncle->_col == RED)//uncle存在且为红
{
//变色处理
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
//更新cur继续向上处理
cur = grandfather;
parent = cur->_parent;
}
else//uncle不存在或者存在且为黑
{
if (cur == parent->_left)
{
//g
//pu
//c
//以g为旋转点进行右单旋
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
//g
//pu
//c
//进行左右双旋
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
//旋转+变色后链接祖先节点的节点为黑,必然不会发生连续红色节点的情况直接break;
break;
}
}
}
//如果持续更新变色到根
_root->_col = BLACK;
return true;
}
2.3 红黑树的验证
>检查每条路径的黑色节点是否相等,是否有连续的红色节点
//检查每条路径的黑色节点是否相等,是否有连续的红色节点
bool Check(Node* root, int blackNum, const int refNum)
{
if (root == nullptr)
{
// 前序遍历⾛到空时,意味着⼀条路径⾛完了
//cout << blackNum << endl;
if (refNum != blackNum)
{
cout << "存在黑色结点的数量不相等的路径" << endl;
return false;
}
return true;
}
// 检查孩⼦不太⽅便,因为孩⼦有两个,且不⼀定存在,反过来检查⽗亲就⽅便多了
if (root->_col == RED && root->_parent->_col == RED)
{
cout << root->_kv.first << "存在连续的红色节点" << endl;
return false;
}
if (root->_col == BLACK)
{
blackNum++;
}
return Check(root->_left, blackNum, refNum)
&& Check(root->_right, blackNum, refNum);
}
>检查平衡
//检查平衡
bool IsBalance()
{
if (_root == nullptr)
return true;
if (_root->_col == RED)
return false;
// 参考值
int refNum = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
{
++refNum;
}
cur = cur->_left;
}
return Check(_root, 0, refNum);
}
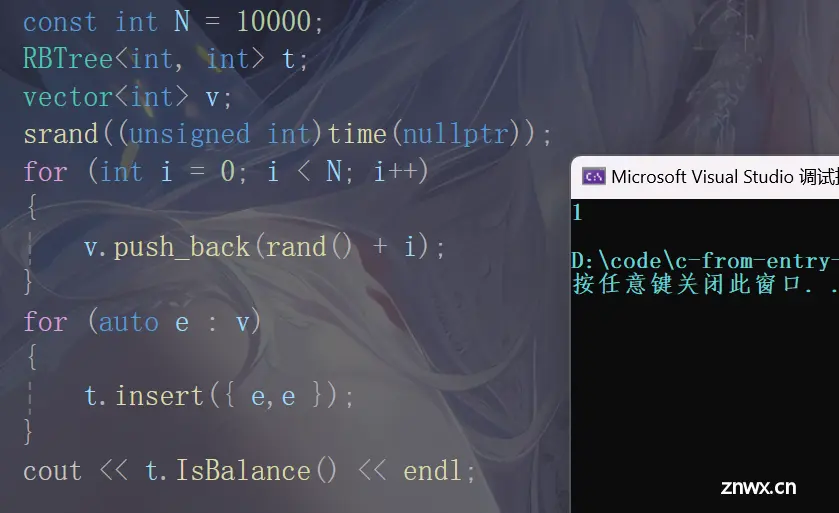
>插入一万个随机数看看是否平衡
void testInert()
{
const int N = 10000;
RBTree<int, int> t;
vector<int> v;
srand((unsigned int)time(nullptr));
for (int i = 0; i < N; i++)
{
v.push_back(rand() + i);
}
for (auto e : v)
{
t.insert({ e,e });
}
cout << t.IsBalance() << endl;
}

2.4 红黑树的其他简单接口
<code>//默认构造
RBTree() = default;
//拷贝构造
RBTree(const RBTree<K,V>& rbt)
{
_root=_copy(rbt._root);
}
// 赋值重载
RBTree<K, V>& operator=(RBTree<K, V> tmp)
{
std::swap(_root, tmp._root);
return *this;
}
//中序遍历
void InOrder()
{
_InOrder(_root);
}
//二叉树的析构
~RBTree()
{
_Destroy(_root);
}
private:
//递归拷贝
Node* _copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newNode = new Node(root->_kv);
newNode->_left = _copy(root->_left);
newNode->_right = _copy(root->_right);
return newNode;
}
//中序遍历
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << "<" << root->_kv.first << "," << root->_kv.second << ">" << endl;
_InOrder(root->_right);
}
//二叉树的销毁
void _Destroy(Node* root)
{
if (root == nullptr)
return;
_Destroy(root->_left);
_Destroy(root->_right);
delete root;
}
3、红黑树完整源码

<code>#pragma once
#include<iostream>
using namespace std;
//枚举类型定义颜色
enum Colour
{
RED,
BLACK
};
//节点结构(默认存储pair类型的key/val结构)
template<class K, class V>
struct RBTreeNode
{
RBTreeNode(const pair<K, V>& kv)
:_kv(kv)
, _parent(nullptr)
, _left(nullptr)
, _right(nullptr)
,_col(RED)
{}
pair<K, V> _kv;
RBTreeNode* _parent;
RBTreeNode* _left;
RBTreeNode* _right;
Colour _col;//初始化为红色
};
//红黑树
template<class K,class V>
class RBTree
{
typedef RBTreeNode<K,V> Node;
public:
//默认构造
RBTree() = default;
//拷贝构造
RBTree(const RBTree<K,V>& rbt)
{
_root=_copy(rbt._root);
}
// 赋值重载
RBTree<K, V>& operator=(RBTree<K, V> tmp)
{
std::swap(_root, tmp._root);
return *this;
}
//中序遍历
void InOrder()
{
_InOrder(_root);
}
//二叉树的析构
~RBTree()
{
_Destroy(_root);
}
//红黑树的查找
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < key)
{
cur = cur->_right;
}
else if (cur->_kv.first > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
//红黑树的插入
bool insert(const pair<K, V>& kv)
{
//如果树为空,在根插入并且颜色为黑色
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
//树不为空按搜索树规则先进行插入
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (kv.first < cur->_kv.first)//小往左走
{
parent = cur;
cur = parent->_left;
}
else if (kv.first > cur->_kv.first)//大往右走
{
parent = cur;
cur = parent->_right;
}
else
{
return false;//不支持相同元素的插入
}
}
cur = new Node(kv);
cur->_col = RED;
if (kv.first < parent->_kv.first)//K小插入在左边
parent->_left = cur;
else//K大插入在右边
parent->_right = cur;
cur->_parent = parent;
//插入后进行维护红黑树规则的逻辑
//parent存在且为红
while (parent&& parent->_col == RED)
{
Node* grandfather = parent->_parent;
//p在g的右边
if (parent == grandfather->_right)
{
//g
//up
Node* uncle = grandfather->_left;
if (uncle&& uncle->_col == RED)//uncle存在且为红
{
//变色处理
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
//更新cur继续向上处理
cur = grandfather;
parent = cur->_parent;
}
else//uncle不存在或者存在且为黑
{
if (cur == parent->_right)
{
//g
//up
// c
//以g为旋转点进行左单旋
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
//g
//up
// c
//进行右左双旋
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
//旋转+变色后链接祖先节点的节点为黑,必然不会发生连续红色节点的情况直接break;
break;
}
}
else//p在g的左边
{
//g
//pu
Node* uncle = grandfather->_right;
if (uncle&& uncle->_col == RED)//uncle存在且为红
{
//变色处理
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
//更新cur继续向上处理
cur = grandfather;
parent = cur->_parent;
}
else//uncle不存在或者存在且为黑
{
if (cur == parent->_left)
{
//g
//pu
//c
//以g为旋转点进行右单旋
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
//g
//pu
//c
//进行左右双旋
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
//旋转+变色后链接祖先节点的节点为黑,必然不会发生连续红色节点的情况直接break;
break;
}
}
}
//如果持续更新变色到根
_root->_col = BLACK;
return true;
}
//检查平衡
bool IsBalance()
{
if (_root == nullptr)
return true;
if (_root->_col == RED)
return false;
// 参考值
int refNum = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
{
++refNum;
}
cur = cur->_left;
}
return Check(_root, 0, refNum);
}
private:
//右单旋
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* pParent = parent->_parent;
parent->_left = subLR;
if (subLR)//如果不为空
subLR->_parent = parent;
subL->_right = parent;
parent->_parent = subL;
if (pParent == nullptr)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (pParent->_left == parent)
{
pParent->_left = subL;
}
else
{
pParent->_right = subL;
}
subL->_parent = pParent;
}
}
//左单旋
void RotateL(Node* parent)
{
Node* pParent = parent->_parent;
Node* subR = parent->_right;
Node* subRL = subR->_left;
subR->_left = parent;
parent->_parent = subR;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
if (pParent == nullptr)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (pParent->_left == parent)
{
pParent->_left = subR;
}
else
{
pParent->_right = subR;
}
subR->_parent = pParent;
}
}
//检查每条路径的黑色节点是否相等,是否有连续的红色节点
bool Check(Node* root, int blackNum, const int refNum)
{
if (root == nullptr)
{
// 前序遍历⾛到空时,意味着⼀条路径⾛完了
//cout << blackNum << endl;
if (refNum != blackNum)
{
cout << "存在黑色结点的数量不相等的路径" << endl;
return false;
}
return true;
}
// 检查孩⼦不太⽅便,因为孩⼦有两个,且不⼀定存在,反过来检查⽗亲就⽅便多了
if (root->_col == RED && root->_parent->_col == RED)
{
cout << root->_kv.first << "存在连续的红色节点" << endl;
return false;
}
if (root->_col == BLACK)
{
blackNum++;
}
return Check(root->_left, blackNum, refNum)
&& Check(root->_right, blackNum, refNum);
}
//递归拷贝
Node* _copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newNode = new Node(root->_kv);
newNode->_left = _copy(root->_left);
newNode->_right = _copy(root->_right);
return newNode;
}
//中序遍历
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << "<" << root->_kv.first << "," << root->_kv.second << ">" << endl;
_InOrder(root->_right);
}
//二叉树的销毁
void _Destroy(Node* root)
{
if (root == nullptr)
return;
_Destroy(root->_left);
_Destroy(root->_right);
delete root;
}
private:
Node* _root=nullptr;
};
4、完结散花
好了,这期的分享到这里就结束了~
如果这篇博客对你有帮助的话,可以用你们的小手指点一个免费的赞并收藏起来哟~
如果期待博主下期内容的话,可以点点关注,避免找不到我了呢~
我们下期不见不散~~
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。