【C++从小白到大牛】栈和队列(优先级队列)
可涵不会debug 2024-08-27 14:05:03 阅读 71

目录
引言:
使用方法篇:
stack:
queue
priority_queue
使用方法:
模拟实现篇:
stack:
原码:
queue
原码:
priority_queue
插入和删除数据的思想:
仿函数实现比较
原码:
引言:
本文主要讲解C++ STL库中stack、queue、priority_queue的使用方法和模拟实现。
我们首先需要对stack、queue进行定性,他们跟我们之前讲的string、vector、list一样都是容器吗?
其实并不是。虽然stack和queue中也可以存放元素,列只是对其他容器的接口进行了封装,STL中stack和queue默认使用deque,因为deque这个容器几乎包含了vector和list的所有接口但在STL中并没有将其划分在容器的行列,而是将其称为容器适配器!
适配器是一种设计模式(设计模式是一套被反复使用的、多数人知晓的、经过分类编目的、代码设计经验的总结),该种模式是将一个类的接口转换成客户希望的另外一个接口。
使用方法篇:
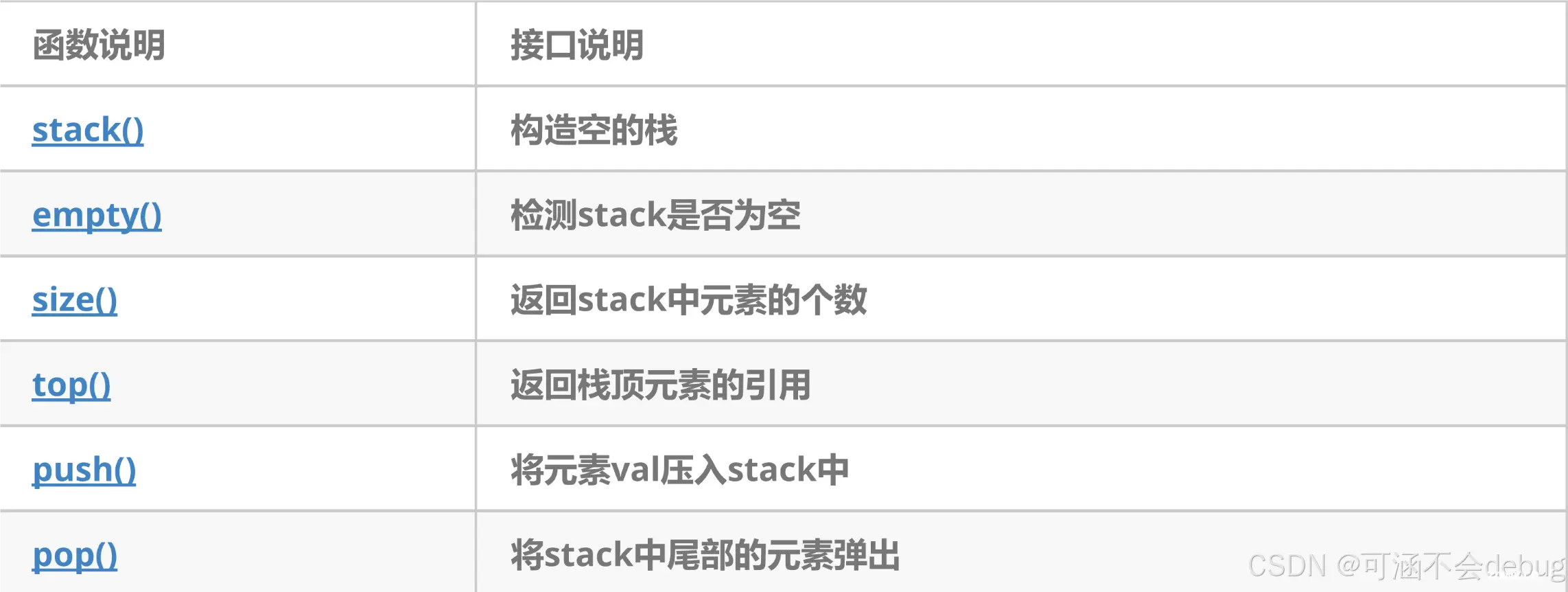
stack:
stack是一种容器适配器,专门用在具有后进先出操作的上下文环境中,其删除只能从容器的一端进行元素的插入与提取操作。
queue
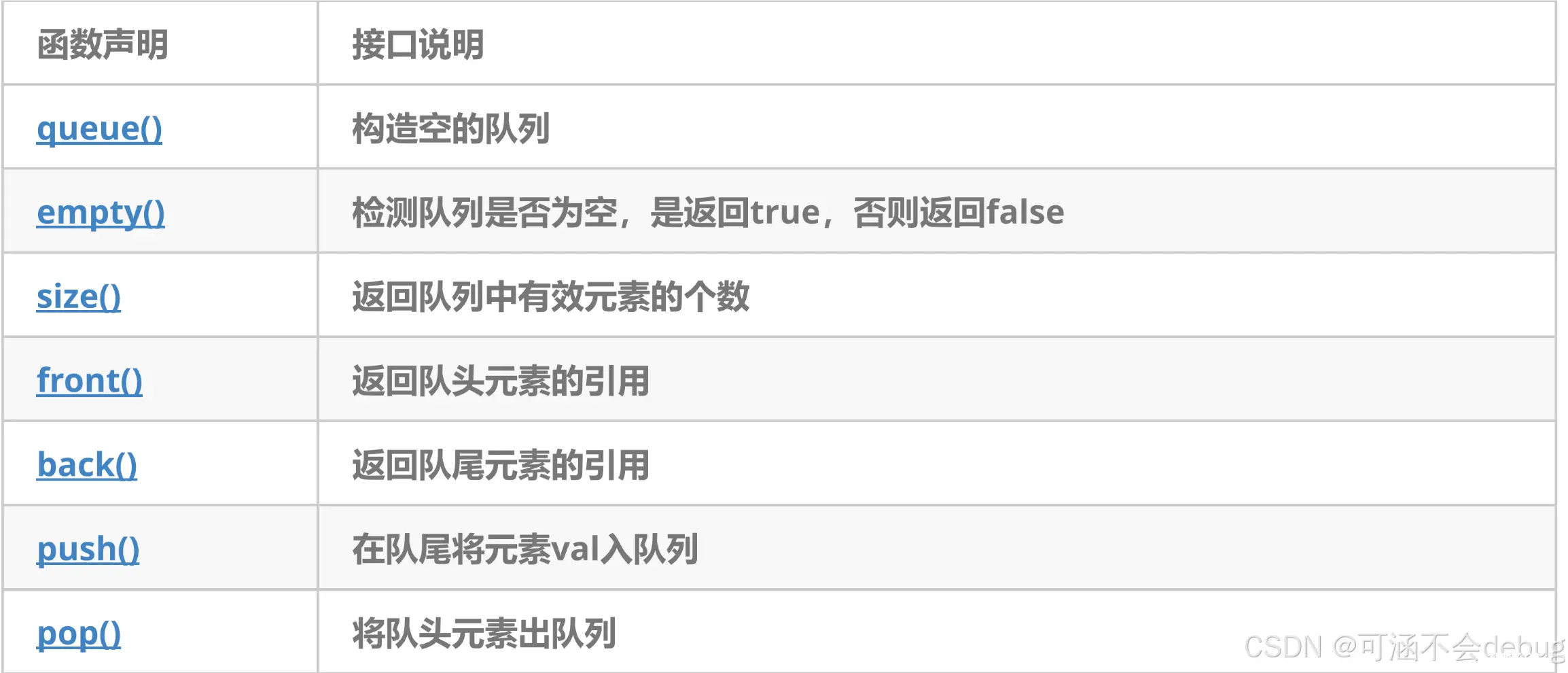
队列是一种容器适配器,专门用于在FIFO上下文(先进先出)中操作,其中从容器一端插入元素,另一端提取元素。
priority_queue
1. 优先队列是一种容器适配器,根据严格的弱排序标准,它的第一个元素总是它所包含的元素中最大的。
2. 此上下文类似于堆,在堆中可以随时插入元素,并且只能检索最大堆元素(优先队列中位于顶部的元素)。
使用方法:
优先级队列默认使用vector作为其底层存储数据的容器,在vector上又使用了堆算法将vector中元素构造成堆的结构,因此priority_queue就是堆,所有需要用到堆的位置,都可以考虑使用priority_queue。注意:默认情况下priority_queue是大堆。
| 函数说明 | 接口说明 |
| empty( ) | 检测优先级队列是否为空,是返回true,否则返回false |
| top( ) | 返回优先级队列中最大(最小元素),即堆顶元素 |
| push(x) | 在优先级队列中插入元素x |
| pop() | 删除优先级队列中最大(最小)元素,即堆顶元素 |
模拟实现篇:
stack:
1、stack是作为容器适配器被实现的,容器适配器即是对特定类封装作为其底层的容器,并提供一组特定的成员函数来访问其元素,将特定类作为其底层的,元素特定容器的尾部(即栈顶)被压入和弹出。
2. stack的底层容器可以是任何标准的容器类模板或者一些其他特定的容器类,这些容器类应该支持以下操作:
empty:判空操作
back:获取尾部元素操作
push_back:尾部插入元素操作
pop_back:尾部删除元素操作
3. 标准容器vector、deque、list均符合这些需求,默认情况下,如果没有为stack指定特定的底层容器,默认情况下使用deque。
因为是容器适配器,所以只是对其他容器的接口进行了封装,因此模拟实现起来非常简单,直接调用原先容器的接口即可,本质上是一种复用!
原码:
<code>namespace kehan
{
template<class T, class Con = deque<T>>
class stack
{
public:
void push(const T& x)
{
_c.push_back(x);
}
void pop()
{
_c.pop_back();
}
T& top()
{
return _c.back();
}
const T& top()const
{
return _c.back();
}
size_t size()const
{
return _c.size();
}
bool empty()const
{
return _c.empty();
}
private:
Con _c;
};
}
queue
1、队列作为容器适配器实现,容器适配器即将特定容器类封装作为其底层容器类,queue提供一组特定的成员函数来访问其元素。元素从队尾入队列,从队头出队列。
2、 底层容器可以是标准容器类模板之一,也可以是其他专门设计的容器类。该底层容器应至少支持以下操作:
empty:检测队列是否为空
size:返回队列中有效元素的个数
front:返回队头元素的引用
back:返回队尾元素的引用
push_back:在队列尾部入队列
pop_front:在队列头部出队列
3. 标准容器类deque和list满足了这些要求。默认情况下,如果没有为queue实例化指定容器类,则使用标准容器deque。
跟stack同理,都是容器适配器,因此直接复用接口即可,与stack使用一些不同的接口,两者区别仅此而已,实现也比较简单。
原码:
namespace kehan
{
template<class T, class Con = deque<T>>
class queue
{
public:
void push(const T& x)
{
_c.push_back(x);
}
void pop()
{
_c.pop_front();
}
T& back()
{
return _c.back();
}
const T& back()const
{
return _c.back();
}
T& front()
{
return _c.front();
}
const T& front()const
{
return _c.front();
}
size_t size()const
{
return _c.size();
}
bool empty()const
{
return _c.empty();
}
private:
Con _c;
};
};
priority_queue
1、 优先队列被实现为容器适配器,容器适配器即将特定容器类封装作为其底层容器类,queue提供一组特定的成员函数来访问其元素。元素从特定容器的“尾部”弹出,其称为优先队列的顶部。
2、 底层容器可以是任何标准容器类模板,也可以是其他特定设计的容器类。容器应该可以通过随机访问迭代器访问,并支持以下操作:
empty():检测容器是否为空
size():返回容器中有效元素个数
front():返回容器中第一个元素的引用
push_back():在容器尾部插入元素
pop_back():删除容器尾部元素
3、 标准容器类vector和deque满足这些需求。默认情况下,如果没有为特定的priority_queue类实例化指定容器类,则使用vector。
注意优先级队列本质上其实是一个堆!默认是大根堆,可以根据自己的需求更改是大根堆还是小根堆(由仿函数实现)。
因为优先级队列的底层是堆,因此我们在一边push数据,一边建堆。
插入和删除数据的思想:
因此这里的插入数据用到了在数据尾部插入,采用向上调整算法,保证插入过后仍然是堆;
删除数据同理,删除数据指的就是删除堆顶位置的元素,我们先将堆顶位置的元素和堆里面最后一个位置的元素进行交换,然后将最后一个位置的元素pop掉(就是原先的堆顶元素),接着再用向下调整算法进行保证还是一个堆。
仿函数实现比较
仿函数本质上是对操作符()括号的重载,因为有两个括号比较像函数,所以取名为仿函数,但他本质上是一个类!
通过仿函数控制类里面的数据比较逻辑,实现回调。

原码:
<code>namespace kehan
{
//利用仿函数进行比较
template <class T>
class greater
{
public:
bool operator()(T x, T y)
{
return x > y;
}
};
template <class T>
class less
{
public:
bool operator()(T x, T y)
{
return x < y;
}
};
template <class T, class Container = vector<T>, class Compare = less<T>>
class priority_queue
{
public:
//向上调整算法
void adjustup(int child)
{
while (child > 0)
{
int parent = (child - 1) / 2;
if (comp(c[parent], c[child]))//建大堆
{
swap(c[parent], c[child]);
child = parent;
}
else
break;
}
}
//向下调整算法
void adjustdown(int parent)
{
int child = parent * 2 + 1;
if (child+1 < c.size() && comp(c[child] ,c[child + 1])) child++;
while (child < c.size())
{
if (comp(c[parent], c[child]))
{
swap(c[parent], c[child]);
parent = child;
}
else
break;
child = parent * 2 + 1;
if (child+1 < c.size() && comp(c[child], c[child + 1])) child++;
}
}
bool empty() const
{
return c.empty();
}
size_t size() const
{
return c.size();
}
const T& top() const
{
return c[0];
}
void push(const T& x)
{
//这里的push就是一个建堆的过程
c.push_back(x);
adjustup(c.size()-1);
}
void pop()
{
swap(c[0], c[c.size() - 1]);
c.pop_back();
adjustdown(0);
}
private:
Container c;
Compare comp;
};
};
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。