前言：在学习之前的数据结构的时候，我们使用的数据量都不是很大，但是在生活中，我们常常面临着要处理大量数据结果并得出最终结果，那么有没有什么数据结构可以帮助我们实现这样的功能呢？

✨✨✨这里是秋刀鱼不做梦的BLOG

✨✨✨想要了解更多内容可以访问我的主页秋刀鱼不做梦-CSDN博客

那么在开始学习处理大量数据的数据结构之前，先让我们看一下本文大致的讲解内容：

目录

1.位图

        （1）位图的概念

        （2）位图的实现

        （3）位图的应用

2.布隆过滤器

        （1）布隆过滤器的概念

        （2）布隆过滤器的实现

        （3）布隆过滤器的优缺点

        （4）布隆过滤器的应用

3.海量数据处理中的应用场景

        （1）位图在海量数据处理中的应用

        （2）布隆过滤器在海量数据处理中的应用

1.位图

        （1）位图的概念

        首先我们要学习的数据结构就是位图，那么读者会发问了？什么是位图呢？以下是位图的概念：

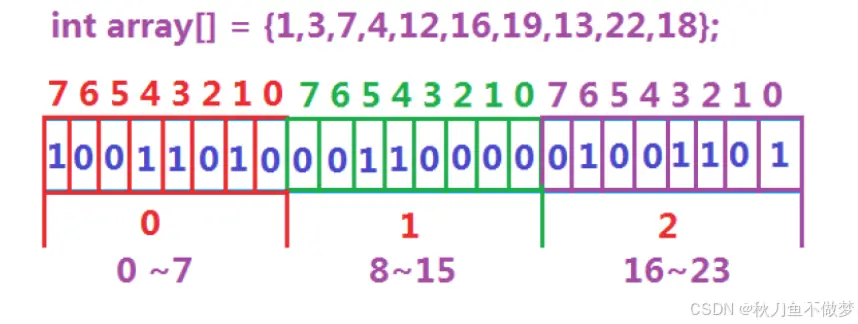
        位图是一种空间优化的数据结构，适合用于表示大量数据的存在性。其基本思想是将每个数据用二进制的“0”或“1”表示，“1”表示数据存在，“0”表示数据不存在。位图特别适合用于对海量整数数据进行存在性检查或排序操作。

如图：

        通过上述的描述，相信读者对位图有了一定的了解，在了解了位图的定义之后，让我们用一个实例再来说明一下位图的作用：

        假设有40亿个不重复的无符号整数，我们需要判断某个数是否存在于这40亿个数中。通常的解决方法可能是将数据存储在数组或列表中，然后进行遍历或使用二分查找。然而，这两种方式的时间复杂度较高，而位图通过将每个整数映射到相应的比特位，能以较低的空间消耗实现高效查询。如上例，假设数据集中有40亿个整数，使用位图只需要约512MB的空间即可完成数据存储和查询。

        至此，我们就对位图有了初步的了解了！

        （2）位图的实现

        当我们了解了位图是什么之后，现在让我们自我实现一下位图。

——位图的核心是将整数映射到一个数组的特定位置并通过位操作来设置或获取该位置的值。下面是位图实现的代码：

<code>public class MyBitSet {

private byte[] elem;

private int usedSize;

// 构造函数，初始化位图大小

public MyBitSet(int n) {

elem = new byte[n / 8 + 1]; // 位图大小：n个比特位

}

// 设置某一位为1，表示对应的值存在

public void set(int val) {

int arrayIndex = val / 8;

int bitIndex = val % 8;

elem[arrayIndex] |= (1 << bitIndex);

usedSize++;

}

// 检查某个值是否存在

public boolean get(int val) {

int arrayIndex = val / 8;

int bitIndex = val % 8;

return (elem[arrayIndex] & (1 << bitIndex)) != 0;

}

// 重置某一位为0，表示对应的值不存在

public void reSet(int val) {

int arrayIndex = val / 8;

int bitIndex = val % 8;

elem[arrayIndex] &= ~(1 << bitIndex);

usedSize--;

}

// 获取已使用的比特位数量

public int getUsedSize() {

return usedSize;

}

}

        根据上边的注释，我们可以很好的理解如何去实现一个位图，不过在此我们还是对上述的代码进行解释：

elem 数组用于存储比特位信息，每个字节（8位）可存储8个整数的存在状态。

set() 方法通过位运算将某一位设置为1。

get() 方法通过按位与运算检查某位是否为1，从而判断对应的整数是否存在。

reSet() 方法则将某一位重置为0，表示数据不存在。

        这样我们就了解了如何去自我实现位图了！

        （3）位图的应用

        了解完了什么是位图和如何去实现一个位图之后，读者可以会发问到：位图除了可以处理大量数据之外，位图在生活中还有什么用处呢？

以下为位图的一些应用场景：

快速判断数据是否存在：例如，在大数据集群中判断某个用户ID是否存在。数据去重：通过位图可以快速判断某数据是否已经存在，从而避免重复操作。集合运算：位图能够高效地实现集合的并集、交集等操作，尤其适合用于处理大规模的集合数据。排序和去重：位图可以用于对大量整数进行排序和去重操作，例如，系统中磁盘块的标记操作。

        这样我们就了解了位图的应用了！

2.布隆过滤器

       同位图一样，在正式开始学习布隆过滤器之前，先让我们了解一下什么是布隆过滤器

        （1）布隆过滤器的概念

        布隆过滤器是一种概率型的数据结构，主要用于集合查询。与位图不同，布隆过滤器能够高效地判断某个元素是否“可能存在”或“肯定不存在”。它的特点是通过多个哈希函数将元素映射到位数组的不同位置，并设置对应比特位为1。当查询一个元素时，如果所有哈希函数映射的比特位都为1，则认为该元素“可能存在”；若有一个比特位为0，则该元素“肯定不存在”。

如图：

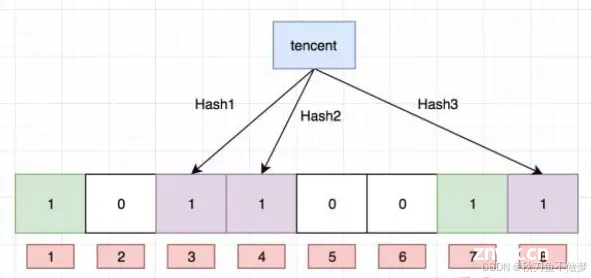
        光看上述的文字解释可能有点晦涩难懂，那么这里我们使用一个生活中的案例来对其进行解释：

        想象你在家里开派对，邀请了50位朋友，但你不记得是否某位朋友已经到达。你可以通过查看他们是否签了名（签名簿）来判断。每个朋友到达后，你会要求他们签名在一个特定的位置上，这类似于哈希函数的映射。如果你检查到所有他们应签的位都已经被签了，那就可能意味着他们已经来过了，但也可能是误判。

        相信通过上述的解释之后，读者可以对布隆过滤器有了更好的理解！

        （2）布隆过滤器的实现

        了解完了布隆过滤器的定义之后，现在让我们自我实现一个布隆过滤器。

        布隆过滤器的基本实现包含一个位数组和多个不同的哈希函数。每个哈希函数将输入的元素映射到位数组的一个位置，并将该位置的比特位设置为1。

下面是实现布隆过滤器的代码：

<code>import java.util.BitSet;

// 简单哈希类

class SimpleHash {

private int cap; // 哈希表的大小

private int seed; // 哈希种子

// 构造函数，初始化哈希表大小和种子

public SimpleHash(int cap, int seed) {

this.cap = cap;

this.seed = seed;

}

// 哈希函数

public int hash(String value) {

int result = 0;

int len = value.length();

// 遍历字符串的每一个字符

for (int i = 0; i < len; i++) {

result = seed * result + value.charAt(i); // 计算哈希值

}

// 返回哈希值与 cap-1 的位与操作结果

return (cap - 1) & result;

}

}

// 布隆过滤器类

public class BloomFilter {

private static final int DEFAULT_SIZE = 1 << 24; // 位数组大小

private static final int[] seeds = {5, 7, 11, 13, 31, 37, 61}; // 哈希种子

private BitSet bits = new BitSet(DEFAULT_SIZE); // 位数组

private SimpleHash[] func = new SimpleHash[seeds.length]; // 哈希函数数组

// 构造函数，初始化哈希函数

public BloomFilter() {

for (int i = 0; i < seeds.length; i++) {

func[i] = new SimpleHash(DEFAULT_SIZE, seeds[i]); // 根据种子初始化 SimpleHash

}

}

// 插入数据

public void set(String value) {

for (SimpleHash f : func) {

bits.set(f.hash(value)); // 使用每个哈希函数设置位

}

}

// 查询数据是否存在

public boolean contains(String value) {

for (SimpleHash f : func) {

if (!bits.get(f.hash(value))) {

return false; // 只要有一个哈希函数返回 false，就说明不在集合中

}

}

return true; // 有可能误判

}

// 主函数，用于测试

public static void main(String[] args) {

BloomFilter filter = new BloomFilter();

filter.set("test"); // 插入字符串 "test"

System.out.println(filter.contains("test")); // 输出: true，表示 "test" 存在

System.out.println(filter.contains("hello")); // 输出: false，表示 "hello" 不存在

}

}

代码解释：

SimpleHash 类实现了哈希函数，通过不同的种子（seed）保证多个哈希函数的多样性。

BloomFilter 类使用位数组和多个哈希函数实现数据的插入与查询操作。set() 方法将数据插入布隆过滤器，而 contains() 方法则检查数据是否可能存在。

布隆过滤器的查询可能存在误判，但能保证元素“肯定不存在”的准确性。

这样我们就大致的了解了如何去自我实现一个布隆过滤器了！

        （3）布隆过滤器的优缺点

        从上述的布隆过滤器的自我实现中，我们就可以发现布隆过滤器的一些优点和缺点，那么布隆过滤器有哪些优缺点呢？

优点：

高效的空间利用：布隆过滤器能够通过少量的空间判断数据是否存在，大大减少了内存占用。

快速查询：插入和查询的时间复杂度为O(K)，其中K为哈希函数的个数，与数据量大小无关。

并行化处理：多个哈希函数的操作可以并行执行，提高了性能。

缺点：

误判：布隆过滤器可能会误判某些不存在的元素为存在，但它能保证不存在的元素一定不会被误判为存在。

不支持删除：一旦元素被插入布隆过滤器，无法删除，因为删除操作可能会误删除其他哈希值相同的元素。

        （4）布隆过滤器的应用

        通过上述对布隆过滤器的解释，我相信读者可以对布隆过滤器有一定的了解了，那么布隆过滤器有哪些应用呢？

布隆过滤器在以下场景中被广泛使用：

网络爬虫的URL去重：在大规模的网络爬虫中，布隆过滤器用于判断某个URL是否已经被访问过，防止重复爬取。

垃圾邮件过滤：布隆过滤器用于记录垃圾邮件发送者的地址，并在邮件服务器上快速过滤垃圾邮件。

数据库缓存穿透：在大规模分布式系统中，布隆过滤器可以用于防止频繁的数据库查询，减少缓存穿透的风险。

        这样我们就了解了布隆过滤器的应用场景了！

3.海量数据处理中的应用场景

        从上面的文章内容中我们可以知道，位图和布隆过滤器都是对海量数据进行处理的数据结构，那么其在海量数据处理中的应用场景有哪些呢？

        （1）位图在海量数据处理中的应用

        位图可以处理非常庞大的数据集，特别是在内存有限的情况下，位图通过其空间效率优势可以快速解决诸如数据去重、集合运算等问题。例如，假设有两个包含100亿个整数的文件，我们只有1GB的内存，可以通过位图来实现这两个集合的交集、并集等操作。

案例：找到只出现一次的整数

// 假设我们有一个包含100亿个整数的文件，下面的代码实现了位图的简单应用

MyBitSet bitSet = new MyBitSet(10000000000); // 10 billion bits

for (int num : nums) {

if (!bitSet.get(num)) {

bitSet.set(num); // 如果没有出现过，设置为1

} else {

bitSet.reSet(num); // 如果再次出现，重置为0

}

}

// 遍历 bitSet，输出所有只出现一次的整数

        （2）布隆过滤器在海量数据处理中的应用

        布隆过滤器由于其空间优势和高效的查询能力，在海量数据处理中被广泛应用于去重、快速查询等场景。例如，在网络爬虫中，布隆过滤器用于检测某个URL是否已经访问过，防止重复抓取。

案例：布隆过滤器在URL去重中的应用

BloomFilter filter = new BloomFilter();

for (String url : urls) {

if (!filter.contains(url)) {

// 处理未访问过的 URL

filter.set(url);

}

}

——通过上述的简单案例，希望读者可以对其在海量数据处理中的应用场景有一定的了解。

以上就是本篇文章的全部内容了~~~