4.组合总和lll（LeetCode216）

题目叙述：

找出所有相加之和为 <code>n 的 k 个数的组合，且满足下列条件：

<li>只使用数字1到9
• 每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

输入: k = 3, n = 7

输出: [[1,2,4]]

解释:

1 + 2 + 4 = 7

没有其他符合的组合了。

示例 2:

输入: k = 3, n = 9

输出: [[1,2,6], [1,3,5], [2,3,4]]

解释:

1 + 2 + 6 = 9

1 + 3 + 5 = 9

2 + 3 + 4 = 9

没有其他符合的组合了。

示例 3:

输入: k = 4, n = 1

输出: []

解释: 不存在有效的组合。

在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

提示:

• 2 <= k <= 9
• 1 <= n <= 60

思路：

1.回溯函数的参数以及返回值

• 没有返回值

• 我们需要startindex变量来标志着我们遍历的位置

• 并且需要一个一维数组path来存放当前的结果，一个二维数组result来存储最终的结果集。

• targetSum（int）目标和，也就是题目中的n。

• k（int）就是题目中要求k个数的集合。

• sum（int）为已经收集的元素的总和，也就是path里元素的总和。

• startIndex（int）为下一层for循环搜索的起始位置。

代码如下：

vector<vector<int>> result;

vector<int> path;

void backtracking(int targetSum, int k, int sum, int startIndex)

2.回溯函数的结束条件

• 当我们数组中的元素个数等于k时，就收集到了k个元素，也就是我们满足题目的条件，此时就应该返回了
• 并且，如果此时的targetSum=sum了，就是满足我们题目要求的一个答案，我们就应该收集这个答案了。

代码如下：

if(path.size()==k){

if(sum==targetSum) result.push_back(path);

return;

}

3.单层递归的逻辑

• 此处我们是选择1-9的九个数字，因此单层递归的for循环应该是≤9

for(int i=startindex;i<=9;i++)

• 处理过程就是 path收集每次选取的元素，相当于树型结构里的边，sum来统计path里元素的总和

• 并且，我们还需要有回溯的过程，只要加了的话，我们要回到上一层，重新选择的话，此时我们就应该减回来

代码如下：

for(int i=startindex;i<=9;i++){

path.push_back(i);

sum+=i;

//此时这里是i+1，因为元素不能够重复取

backtracking(targetSum,k,sum,i+1);

//这里是回溯的逻辑，在之前加过的元素，如果我们要回溯到上一层再操作，就要减回来

sum-=i;

path.pop_back();

}

• 其实，我们也不需要对sum做加减的操作，直接对传入的参数进行操作，这样相当于是将回溯的逻辑隐藏在了递归函数中，不推荐这种做法。

for(int i=startindex;i<=9;i++){

path.push_back(i);

//此时这里是i+1，因为元素不能够重复取

backtracking(targetSum,k,sum+i,i+1);

path.pop_back();

}

代码：

• 我们根据上面三步的分析，不难得出代码：

class Solution {

public:

vector<int> path;

vector<vector<int>> result;

void backtracking(int targetSum, int k, int startindex, int sum) {

if (path.size() == k) {

if (sum == targetSum)

result.push_back(path);

return;

}

for (int i = startindex; i <= 9; i++) {

sum += i;

path.push_back(i);

backtracking(targetSum, k, i + 1, sum);

//回溯的过程

path.pop_back();

sum -= i;

}

}

vector<vector<int>> combinationSum3(int k, int n) {

//从1开始选

backtracking(n, k, 1, 0);

return result;

}

};

剪枝：

• 在这段代码中，我们可以有两个剪枝的过程。

1. 第一就是如果我们发现当前的sum已经大于targetSum了，那么我们就没有必要就再往下进行遍历了，肯定没有符合条件的k个数相加为n。

void backtracking(int targetSum, int k, int startindex, int sum) {

//发现sum已经大于targetSum了，直接结束本层递归

if(sum>targetSum) return;

if (path.size() == k) {

if (sum == targetSum)

result.push_back(path);

return;

}

for (int i = startindex; i <= 9; i++) {

sum += i;

path.push_back(i);

backtracking(targetSum, k, i + 1, sum);

//回溯的过程

path.pop_back();

sum -= i;

}

}

<li>第二就是单层递归的条件，我们没有必要从startindex遍历到9，只需要遍历到9-(k-path.size())+1即可

• 为什么只需要遍历到9-（k-path.size（））+1就可以了呢？这题的逻辑其实和我们之前讲解的LeetCode77组合总和有异曲同工之妙，我们数组中的元素个数为path.size（）个，我们还需要选择k-path.size（）个元素
• 又因为我们是从i开始,树的最底层,也就是递归的深度,是遍历到9结束,那么这个区间内的元素个数必须≥k-path.size()个
• 这个区间的元素个数为：9-i+1，那么9-i+1>=k-path.size（），可以推出i<=9-（k-path.size()）+1，就是说i至多从这个位置开始遍历

剪枝过程图如下：

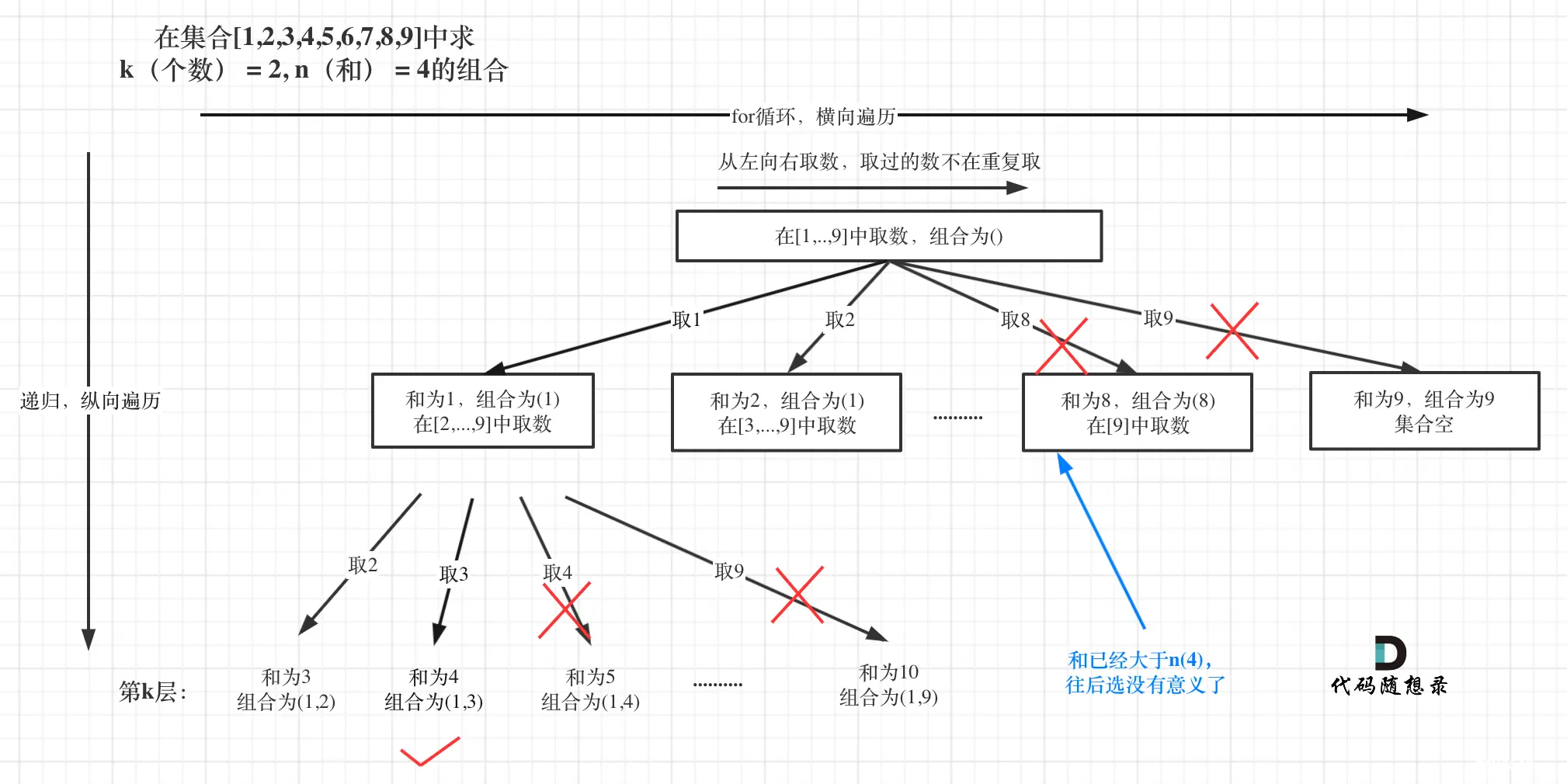
<li>

本文借阅了代码随想录的原图，想要更加深入了解的可以去观看原作者所发的文章！

[代码随想录 (programmercarl.com)]()