目录

1.图的遍历1.广度优先遍历2.深度优先遍历

2.最小生成树1.Kruskal算法2.Prim算法

1.图的遍历

给定一个图G和其中任意一个顶点

v

0

v_0

v0​，从

v

0

v_0

v0​出发，沿着图中各边访问图中的所有顶点，且每个顶 点仅被遍历一次

“遍历”：对结点进行某种操作的意思

1.广度优先遍历

**例如：**现在要找东西，假设有三个抽屉，东西在哪个抽屉不清楚，现在要将其找到，广度优先遍历的做法是：

先将三个抽屉打开，在最外层找一遍将每个抽屉中红色的盒子打开，再找一遍将红色盒子中绿色盒子打开，再找一遍直到找完所有的盒子

注意：每个盒子只能找一次，不能重复找

思考：如何防止节点被重复遍历？

增加一个数组，用于标记是否入过队列，这样可以防止重复遍历

<code>void BFS(const V& src)

{

size_t srci = GetVertexIndex(src);

queue<int> q;

vector<bool> visited(_vertexs.size(), false); // 标记数组

q.push(srci);

visited[srci] = true;

int levelSize = 1; // 控制每层出的数量

while (!q.empty())

{

// 一层一层出

for (size_t i = 0; i < levelSize; i++)

{

int front = q.front();

q.pop();

cout << front << ":" << _vertexs[front] << " ";

// 把front的邻接顶点入队列

for (size_t j = 0; j < _vertexs.size(); j++)

{

if (_matrix[front][j] != MAX_W && visited[j] == false)

{

q.push(j);

visited[j] = true;

}

}

}

cout << endl;

levelSize = q.size();

}

}

2.深度优先遍历

**例如：**现在要找东西，假设有三个抽屉，东西在哪个抽屉不清楚，现在要将其找到，深度优先遍历的做法是：

先将第一个抽屉打开，在最外层找一遍将第一个抽屉中红盒子打开，在红盒子中找一遍将红盒子中绿盒子打开，在绿盒子中找一遍递归查找剩余的两个盒子

**深度优先遍历：**将一个抽屉一次性遍历完(包括该抽屉中包含的小盒子)，再去递归遍历其他盒子 如果给的图不是连通图，以某个顶点为起点没有遍历完成，怎么保证遍历完剩下的顶点？

在visited数组中找没有遍历过的顶点，再次进行遍历

<code>void _DFS(size_t srci, vector<bool>& visited)

{

cout << srci << ":" << _vertexs[srci] << endl;

visited[srci] = true;

for (size_t i = 0; i < _vertexs.size(); i++)

{

if (_matrix[i] != MAX_W && visited[i] == false)

{

_DFS(i, visited);

}

}

}

void DFS(const V& src)

{

size_t srci = GetVertexIndex(src);

vector<bool> visited(_vertexs.size(), false);

_DFS(srci, visited);

// 处理存在不连通的情况

for (size_t i = 0; i < _vertexs.size(); i++)

{

if (!visited[i])

{

_DFS(i, visited);

}

}

}

2.最小生成树

连通图中的每一棵生成树，都是原图的一个极大无环子图，即：

从其中删去任何一条边，生成树就不在连通反之，在其中引入任何一条新边，都会形成一条回路 若连通图由n个顶点组成，则其生成树必含n个顶点和n-1条边，因此构造最小生成树的准则有三条：

只能使用图中权值最小的边来构造最小生成树

最小的成本让着N个顶点连通 只能使用恰好n-1条边来连接图中的n个顶点选用的n-1条边不能构成回路 构造最小生成树的方法：Kruskal算法和Prim算法，这两个算法都采用了逐步求解的贪心策略贪心算法：

指在问题求解时，总是做出当前看起来最好的选择

即：贪心算法做出的不是整体最优的的选择，而是某种意义上的局部最优解 贪心算法不是对所有的问题都能得到整体最优解

1.Kruskal算法

任给一个有n个顶点的连通网络

N

=

{

V

,

E

}

N=\{V,E\}

N={ V,E}

首先构造一个由这n个顶点组成、不含任何边的图

G

=

{

V

,

N

U

L

L

}

G=\{V,NULL\}

G={ V,NULL}，其中每个顶点自成一个连通分量其次不断从E中取出权值最小的一条边(若有多条任取其一)，若该边的两个顶点来自不同的连通分量，则将此边加入到G中

如此重复，直到所有顶点在同一个连通分量上为止 核心：每次迭代时，选出一条具有最小权值，且两端点不在同一连通分量上的边，加入生成树

Kruskal算法是一种全局贪心的算法 如何判断是否形成环？

并查集 在下图执行Kruskal算法的过程

加了阴影的边属于不断增长的森林A该算法按照边的权重大小依次进行考虑，箭头指向的边是算法每一步考察的边

如果该条边将两颗不同的树连接起来，它就被加入到森林里，从而完成对两棵树的合并

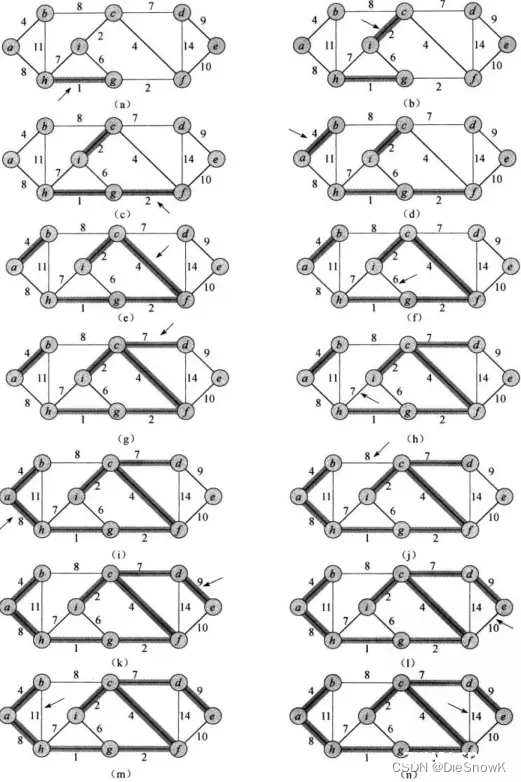
<code>W Kruskal(Self& minTree)

{

size_t n = _vertexs.size();

// 初始化minTree

minTree._vertexs = _vertexs;

minTree._indexMap = _indexMap;

minTree._matrix.resize(n);

for (size_t i = 0; i < n; i++)

{

minTree._matrix[i].resize(n, MAX_W);

}

priority_queue<Edge, vector<Edge>, greater<Edge>> minQueue;

// 建堆排序

for (size_t i = 0; i < n; i++)

{

for (size_t j = 0; j < n; j++)

{

if (i < j && _matrix[i][j] != MAX_W)

{

minQueue.push(Edge(i, j, _matrix[i][j]));

}

}

}

// 选出n-1条边

size_t size = 0;

W totalW = W();

UnionFindSet ufs(n);

while (!minQueue.empty())

{

Edge min = minQueue.top();

minQueue.pop();

// 判环 -> 并查集

if (!ufs.InSameSet(min._srci, min._dsti))

{

cout << _vertexs[min._srci] << "->" \

<< _vertexs[min._dsti] << ":" << min._w << endl;

minTree._AddEdge(min._srci, min._dsti, min._w);

ufs.Union(min._srci, min._dsti); // 入集

size++;

totalW += min._w;

}

else

{

cout << "Forming Ring: ";

cout << _vertexs[min._srci] << "->" \

<< _vertexs[min._dsti] << ":" << min._w << endl;

}

}

if (size == n - 1)

{

return totalW;

}

else

{

return W();

}

}

2.Prim算法

Prim算法的一个性质是集合A中的边总是构成一棵树，这棵树从一个任意的根节点r开始，一直长大到覆盖V中的所有结点时为止

Prim算法思路天然避环算法每一步在连续集合A和A之外的结点的所有边中，选择一条轻量级边加入到A中本策略也属于贪心策略，因为每一步所加入的边都必须是使树的总权重增加量最小的边

Prim算法是一种局部贪心算法 在下图执行Prim算法的过程

初始的根节点为a，加阴影的边和黑色的结点都属于树A在算法的每一步，树中的结点就决定了图的一个切割，横跨该切割的一条轻量级边被加入到树中**例如：**在途中第二步，该算法可以选择将边

(

b

,

c

)

(b, c)

(b,c)加入到树中，也可以将边

(

a

,

h

)

(a, h)

(a,h)加入到树中，因为这两条边都是横跨该切割的轻量级边

<code>W Prim(Self& minTree, const W& src)

{

size_t srci = GetVertexIndex(src);

size_t n = _vertexs.size();

// 初始化minTree

minTree._vertexs = _vertexs;

minTree._indexMap = _indexMap;

minTree._matrix.resize(n);

for (size_t i = 0; i < n; i++)

{

minTree._matrix[i].resize(n, MAX_W);

}

// true & false表示该元素是否在该集合内

vector<bool> X(n, false);

vector<bool> Y(n, true);

X[srci] = true;

Y[srci] = false;

// 从X->Y集合中连接的边里面选出最小的边

priority_queue<Edge, vector<Edge>, greater<Edge>> minQueue;

// 先把srci连接的边添加到队列中

for (size_t i = 0; i < n; i++)

{

if (_matrix[srci][i] != MAX_W)

{

minQueue.push(Edge(srci, i, _matrix[srci][i]));

}

}

size_t size = 0;

W totalW = W();

while (!minQueue.empty())

{

Edge min = minQueue.top();

minQueue.pop();

// 最小边的目标也在X集合，则构成环

if (X[min._dsti])

{

cout << "Forming Ring:";

cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;

}

else

{

cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;

minTree._AddEdge(min._srci, min._dsti, min._w);

X[min._dsti] = true;

Y[min._dsti] = false;

size++;

totalW += min._w;

// 可能最小生成树已经生成，但是多了很多成环边，无须继续遍历

if (size == n - 1)

{

break;

}

// 将目标顶点连接的边加入到队列中

for (size_t i = 0; i < n; i++)

{

if (_matrix[min._dsti][i] != MAX_W && Y[i])

{

minQueue.push(Edge(min._dsti, i, _matrix[min._dsti][i]));

}

}

}

}

// 实际不一定存在最小生成树

if (size == n - 1)

{

return totalW;

}

else

{

return W();

}

}