没有更新完之前，专栏价格为59，更新完毕之后恢复到99. 专栏内包含2024年所有数学建模比赛思路和代码，有些重要比赛着重更新（华数杯、国赛、美赛），小比赛可能会有chatgpt4更新，只需订阅一次。有些文章没有完整代码，请到专栏内查找最新代码和思路。如果比赛结束后没有更新代码（可能会有事情来不及更新）赛后我会统一退款。

2024年第五届“华数杯”专栏地址：https://blog.csdn.net/m0_52343631/category_12482955.html?spm=1001.2014.3001.5482

目录

2024年第五届“华数杯”专栏地址：https://blog.csdn.net/m0_52343631/category_12482955.html?spm=1001.2014.3001.5482

摘要

一、问题重述

二、问题假设

三、符号说明

四、问题分析

五、问题一模型的建立与求解

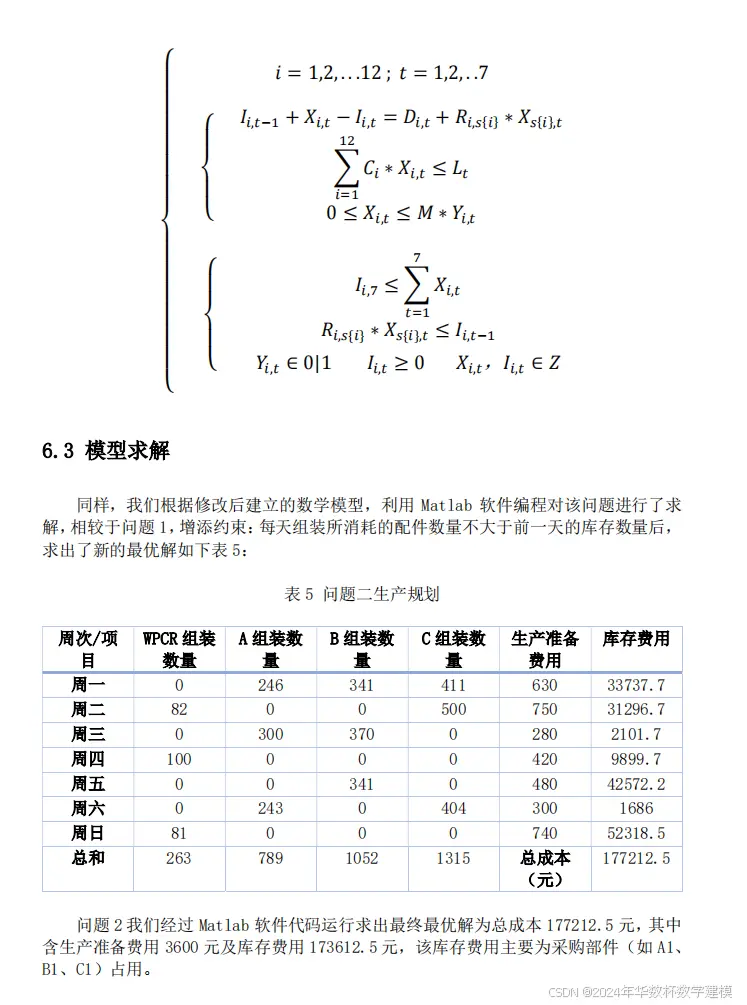
六、问题二模型的建立与求解

七、问题三模型的建立与求解

九、模型评价及推广

十、参考文献

2022年优秀论文

摘要

可在水下移动、具有视觉和感知系统的自来水管道清理机器人（Water pipe

cleaning robot，简称 WPCR）能通过遥控或自主操作方式、使用机械臂代替或辅助人去

完成自来水管道垃圾清理任务。这种装置能及时清理管道，既可提高自来水的品质，也

能够保证水流畅通。该产品正受到水务公司和家庭住户的青睐，因此，对该装置的生产

规划问题应运而生。该问题是一个多级生产与库存管理的问题，需要合理安排每日生产

计划并使库存得到规划才能让此问题得到很好的解决。

问题 1：

首先根据题目信息可知在给定期限一周内开始阶段无任何存货，且期限结

束后也不遗留任何组件库存，那么每日生产计划需得到合理安排刚好用完。当日采购的

零件马上就可以用于组装，组装出来的部件也可以马上用于当日组装成品装置 WPCR。我

们据此建立了目标函数即为每日需要生产的产品生产准备费用与每日剩余库存费用之

和，赋予生产部件数量、是否生产组件、组件库存数量等为决策变量，构建物流平衡方

程：每个时段前一时段库存加当前时段生产量，减去该项目当前时段的需求量和用于组

装其他项目的量等于当前时段库存。决策目标为总成本，给定约束条件，建立优化模型

求解,得出最小成本为 6260.9 元

问题 2：

问题 2 提供了新的条件，即当日需要生产的项目的部件需要提前一天采购

或组装。周一开始时的存货为周日库存，周日结束时同样需要给下周一的生产提供库存

准备。据题我们可将目标生产计划理解为一个周期闭环，周一和周日变得连续，我们在

问题 1的基础上添加了新的约束：每天组装所消耗的配件数量不大于前一天的库存数量，

新增约束后，物流平衡方程无需改变，便可求出最优解，得出的最小成本为 177212.5元。

问题 3：

问题 3 在问题 2 的基础上添加的新的条件，即 210 天内需要进行 7 天的维

修，在维修当天工厂无法进行任何组件的生产，同时任意两次维修的日期必须要间隔 6

天以上，在每次维修过后的 5 天，工厂的生产工时会有一定的增加，在将这些约束加入

问题 2 的优化模型的同时加入一个新的决策变量来表示是否需要维修即可建立起基于

问题 3 的混合整数线性规划，利用 Matlab 对于此模型求解，可得到最优解，求解后可

知最小成本为 5317581 元。

问题 4：

题目给出了前 30 周的历史周订单数据，我们可以根据前 30 周的数据，设

其需求近似的服从正态分布，以此为样本空间，进行区间估计，求出一周中各天在置信

水平为 0.95，显著性水平为 1-0.95=0.05 的单侧置信上限，表示一周内该天 WPCR 需求

落在此区间的概率为 95%。对每周总体 WPCR 需求作为样本空间，进行区间估计，求

出每周需求的置信水平为 0.85，显著性水平为 1-0.85=0.15 的单侧置信上限，表示每周

的 WPCR 需求小于此上限的概率为 85%，据此制定了新的周生产计划，该计划下最小

成本为

177942.5 元。

关键词：

0-1 规划、混合线性整数规划、区间估计、正态分布

一、问题重述

自来水管道清理机器人（Water pipe cleaning robot，简称 WPCR）是一种可在水

下移 动、具有视觉和感知系统、通过遥控或自主操作方式、使用机械臂代替或辅助人去

完成 自来水管道垃圾清理任务的装置。运用这种装置能够及时清理管道，既可提高自

来水的 品质，也能够保证水流畅通，因而越来越受到水务公司和家庭住户的青睐。

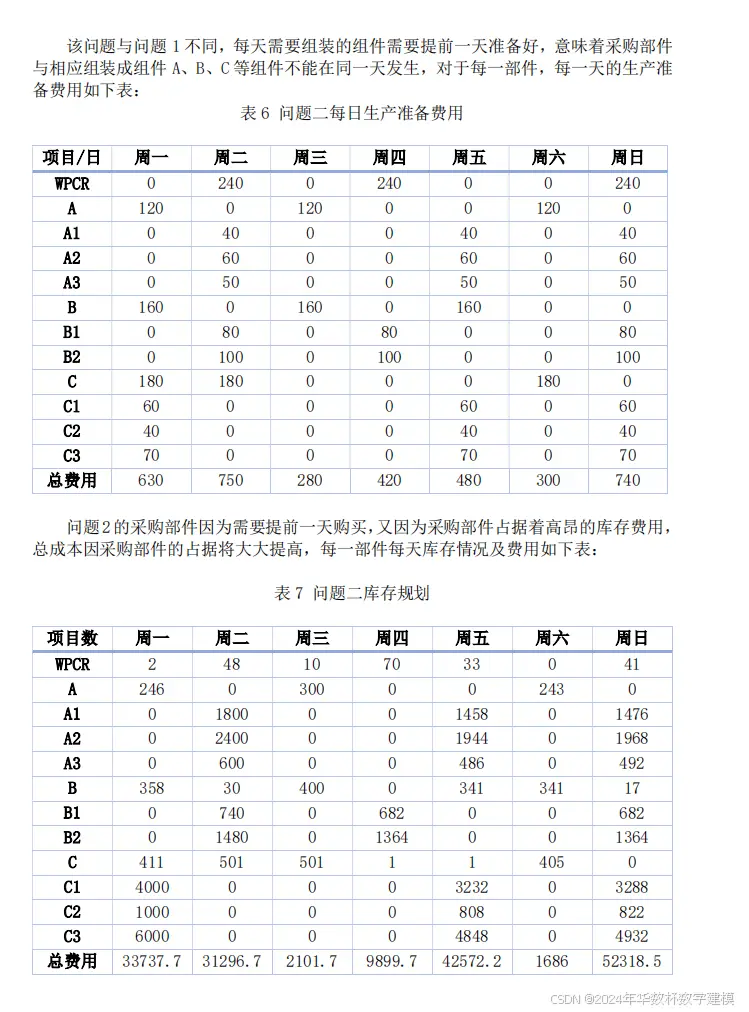
某工厂生产的 WPCR 装置需要用 3 个容器艇（用 A 表示）、4 个机器臂（用 B 表示）、

5 个动力系统（用 C 表示）组装而成。每个容器艇（A）由 6 个控制器（A1）、8 个划

桨 （A2）和 2 个感知器（A3）组成。每个机器臂（B）组成比较复杂，简单可划分为 2

个 力臂组件（B1）和 4 个遥感器（B2）组成。每个动力系统（C）由 8 个蓄电池（C1）、

2 个微型发电机（C2）和 12 个发电螺旋（C3）组成。也就是说组装一个完整的 WPCR

装置，需要 3 个容器艇（A），包括 18 个控制器（A1）、24 个划桨（A2）以及 6 个感

知器（A3）。组装一台 WPCR 需要的其他部件数以此类推。组装 WPCR 所需要的产品统 称

为组件，包括 A 和 A1、A2、A3，B 和 B1、B2，C 和 C1、C2、C3。

该工厂每次生产计划的计划期为一周（即每次按照每周 7 天的订购数量实行订单

生 产），只有最终产品 WPCR 有外部需求，其他组件不对外销售。容器艇（A）、机器臂

（B）、动力系统（C）生产要占用该工厂最为关键的设备，因而严格控制总生产工时。 A、

B、C 的工时消耗分别为 3 时/件、5 时/件和 5 时/件，即生产 1 件 A 需要占用 3 个

工 时，生产 1 件 B 需要占用 5 个个工时，生产 1 件 C 需要占用 5 个工时。每天的

WPCR 外部 需求数及关键设备总工时限制见表 5。

为了顺利生产 WPCR，工厂在某一天生产组件产品时，需要付出一个与生产数量无

关的固定成本，称为生产准备费用。比如第一天生产了 A，则要支付 A 的生产准备费用，

若第二天再生产 A，则需要再支付 A 的生产准备费用。如果某一天结束时某组件有库存

存在，则工厂必须付出一定的库存费用（与库存数量成正比）。数据见表 6。另外，按

照工厂的信誉要求，目前接收的所有订单到期必须全部交货，轻易不能有缺货事件发生。

问题 1：

若该工厂第一天（周一）开始时没有任何组件库存，也不希望第 7 天（周

日）结 束后留下任何组件库存。每天采购的组件马上就可用于组装，组装出来的组件也

可以马 上用于当天组装成 WPCR。若要求总成本最小，请问如何制定每周 7 天的生产计

划？

问题 2：

然而，事实上，组件 A、B、C 需要提前一天生产入库才能组装 WPCR，A1、

A2、A3、B1、B2、C1、C2、C3 也需要提前一天生产入库才能组装 A、B、C。在连续多周

生产情况下，需要统筹规划。比如在周一生产 WPCR 前一天（上周周日）必须事先准备

好组件库存，而且在本周日必须留下必要的组件库存用以保障下周一的生产。每周的

WPCR 需求和关键设备工时限制以及每次生产准备费用和单件库存费用数据见表 5、表

6，请问如何制定每周 7 天的生产计划以求总成本最低？

问题 3：

为了保障生产的持续性，工厂需要在 30 周 210 天里必须设置 7 次停

工检修，每次检修时间为 1 天。检修之后关键设备生产能力有所提高，检修后的第一

天 A、B、C 生产总工时限制将会放宽 10%，随后逐日减少放宽 2%的比例，直至为 0（如

第一天放宽 10%，第二天就放宽 8%，...）。检修日的订单只能提前安排生产，当天不

能生产任何组件。假设每周的关键设备工时限制以及每次生产准备费用和单件库存费用

数据不变，任意两次检修之间要相隔 6 天以上，请问，检修日放在哪几天最为合适（总

成本最小）？

问题 4：在生产实际中，在未知 WPCR 外部需求订单的前提下，公司需要有一个稳妥

的单 周生产计划。接问题 2，表 7 数据视为历史周订单数据，在不知未来某周 7 天

订单数且 继续追求周总成本最小的前提下，如何制定周生产计划，既能够保障每天的

WPCR 订单 均以 95%以上的概率保证正常交付，又能够以 85%以上的概率保证整周的

WPCR 订单能 正常交付？

二、问题假设

1.假设组装产品 WPCR、采购小部件（如𝐴

１

、

𝐵

１

）不消耗时间，只有关键设备 A、B、C

的组装需要消耗工时。

2.假设总成本仅含生产准备费用及库存费用。

3.假设有关原材料、人力和能量等直接成本作为常数不予考虑。

4.假设检修间隔六天以上实际意义为若周一检修，那么周日也可以检修。

5.假设问题三条件中第 1 天的初始存货为第 210 天库存。

6.假设 30 周历史订单周一至周日 WPCR 需求服从正态分布。

三、符号说明

四、问题分析

4.1 问题一的分析

该题目需考虑在有限计划时间内，给定产品在期限内的外部需求及产品生产费用和

相关库存费用及关键设备工时限制后，确定每一生产项目的期限内的生产批量。

问题给定期限一周，假设了周一开始时及周日结束后均无任何组件库存，且采购部

件、组装 WPCR 均不消耗时间，仅组装设备 A、B、C 需消耗工时。每天采购组件及组

装 WPCR 均可在当日完成。

为使总成本费用最小，我们使在期限一周内的 WPCR 产品的总产量刚好等于产品

总需求量。考虑到产品 A、B、C 及 WPCR 的生产准备费用及库存费用的差异，我们

将每日是否生产 A、B、C 及 WPCR、每天生产部件数量、每种组件在每天的库存数量

设定为决策变量。目标函数即为每一部件的总生产准备费用和总库存费用之和，我们

在外加每日外部需求和每日产品工时限制等约束条件下，便可以建立问题一的优化模

型。

4.2 问题二的分析

问题二在问题一的基础上增加了一些实际生产中所要考虑的情况。组件 A、B、C 需

要提前一天生产入库才能组装 WPCR，A1、A2、A3、B1、B2、C1、C2、C3 也需要提

前一天生产入库才能组装 A、B、C。在进行连续多周的生产时，要进行必要的规划设计。

可以将周日与周一连接，前日的组件库存必须满足今日的生产消耗，同理今日的组件库

存也必须满足明日的生产消耗。因此不同于问题一，周一若要生产 WPCR 或 A,B,C 时，

前一天必须库存所需的原料组件，周一开始时就会存在有前一天库存的情况，在周日也

会存在库存的情况。对于问题一的决策变量同样适用于问题二，目标函数同样表示总生

产准备费用和总库存费用之和。在问题一的约束条件下，另加当日组件生产所需原料的

前一日的库存要求，可进一步建立问题二的优化模型。

4.3 问题三的分析

问题三是在问题二的基础之上将总的生产时间从一周变为了 210 天，同时增加了需

要对仪器设备进行检修的约束条件，同时在维修之后五天的生产工时限制也会随之而改

变，另外：检修日当天无法生产任何组件以及任意两次维修时间必须间隔 6 天以上，210

天内的维修次数为 7 次。相较于问题二，问题三只是对约束条件做出了一定地增加，由

于目标依旧是让总成本最小，所以目标函数不需要改变，同时因为我们需要知道具体的

检修时间，所以我们在问题二原有的决策变量的基础之上增加任意一天是否需要检修这

一决策变量。对于问题三的约束条件，由于问题三是建立于问题二之上，所以我们只需

要在对问题二原有的约束条件之上做出一点小小的改变的同时，加上关于检修相关的几

个约束条件，即可建立问题三的优化模型。

4.4 问题四的分析

问题四同为问题二的改进问题，在未知 WPCR 外部需求订单的前提下，需要制定一

项稳妥的单周生产计划，需要既能够保障每天的 WPCR 订单均以 95%以上的概率保证

正常交付，又能够以 85%以上的概率保证整周的 WPCR 订单能正常交付，并且考虑到

使总成本最小，在此条件下给出单周生产计划。题目给出了前 30 周的历史周订单数据，

我们可以根据前 30 周的数据，设其需求近似的服从正态分布，以此为样本空间，进行

区间估计，求出一周中各天在置信水平为 0.95，显著性水平为 1-0.95=0.05 的单侧置信

上限，表示一周内该天 WPCR 需求落在此区间的概率为 95%。对每周总体 WPCR 需求

作为样本空间，进行区间估计，求出每周需求的置信水平为 0.85，显著性水平为 1-

0.85=0.15 的单侧置信上限，表示每周的 WPCR 需求小于此上限的概率为 85%。以此上

限来确定生产计划中的 WPCR 需求，能够满足既能够保障每天的 WPCR 订单均以 95%

以上的概率保证正常交付，又能够以 85%以上的概率保证整周的 WPCR 订单能正常交

付的要求。再将此需求与问题二求解的优化模型进行结合，就可保证在满足订单交付要

求的条件下求出使总费用最低的单周生产计划。

五、问题一模型的建立与求解

5.1 模型准备

首先我们对该问题进行分析，根据参考文献[1]可知，本问题是一个有瓶颈设备多级

生产问题，目标产品 WPCR 装置是由容器艇（A）、机械臂（B）、动力系统（C）等组件

组装而成。“多级”，指的是需要考虑产品是通过多个生产阶段(工艺)生产出来的。主要

任务是通过组装生产产品 WPCR，用于满足外部市场需求。于是，我们可以建立 WPCR

装置的构成与组装过程如下图：

六、问题二模型的建立与求解

七、问题三模型的建立与求解

7.1 模型准备

问题三从实质上来说是在问题二的基础之上加上了一定的条件而产生，所以我们只

需要在已经建立的问题二优化模型基础上加上一些因素，同时将将一些原有因素变量化

即可。

对于问题三。我们可以知道是在问题二的基础之上，增加了需要在 210 天内安排 7

次检修这个条件，同时，在每一次维修过后的五天，生产能力都会得到一定的提升，从

而提升了这五天的生产时间上限，在这个条件之下，我们需要注意的是任意两次的维修

需要间隔 6 天以上，另外在维修当天工厂不能够进行任何组件的生产。将这些新增条件

化作求解问题所需的约束条件，同时增加任意一天是否需要对工厂进行检修这一决策变

量即可实现基于问题三的混合整数线性优化模型的建立。

7.2 模型建立

根据问题三分析结果，问题三在问题二的基础之上进行更新条件，因此问题二的约

束条件依然适用。并做出相应改动，将 30 周 210 天看作一个循环体，需要将问题一、

二中的一周天数限制改为 30 周 210 天限制，还需要引入一个当日是否检修的决策变量，

将检修后的工时放宽比例设置为常量建立模型。因此，在继续使用线性规划经典求解时，

目标函数以及约束都要做出相应的改变。

7.3 模型求解

将期限 210 天写入矩阵后，改变原有物流平衡方程，增添新的决策变量，及每天是

否生产，若不生产，则该天作为检修日检修。根据以上约束条件修改好代码后，通过

Matlab 软件对目标函数总成本求得了最优解，则检修日期为

九、模型评价及推广

9.1 模型优点

（1）所建立的优化模型具有可靠的数学基础，综合考虑了各种约束条件，寻得了在

一定范围下的最有参数解，保证了参数的正确性与结果的可靠性及合理性。如模型 1 及

模型 2 采用线性规划求解，将问题简化，求解简单，使用方便作为一个基础简化模型，

其为下一个模型如模型 3、模型 4 打下良好基础，明确给出了物流平衡方程等模型所需

满足的最根本的条件，保证了求解结果的正确性。

（2）模型 3 综合考虑了产品的生产批量与检修问题，增添了新的决策变量参数，

全面且精确，体现了模型易应用易于改进等特点，结合对模型的检验，使得求解结果的

准确度提高。

（3）模型 4 首先对历史订单数据进行拟合，每日订单能保证交付的概率作为了单

侧置信区间的置信上限，运用了区间估计对生产计划进行了制定，这种求解思路满足估

计量的评选标准如无偏性、有效性、相合性。

9.2 模型缺点

模型的不足之处在于所设约束条件过多，人工计算较为复杂；应用场景较为特殊化，

不能直接用于普遍批量问题的最优求解，如除生产准备费用及当日库存费用外一切费用

钧未考虑，部分组件时间忽略未计。其余有关原材料、人力和能量等直接成本作为一个

常数均未考虑。

9.3 模型推广

由于时间有限，本模型还要不足之处，但求得结果还是比较合理，均满足了题设条

件。Matlab 基于问题求解建模代码的特点在于其代码本身的矩阵化编程风格的完美嵌

入，约束条件往往可以不用嵌套循环关键字。代码的简洁也是其得以推广的重要原因之

一，模型给出的物流守恒约束条件关系式适用于绝大多数生产批量-库存安排问题。针

对不同的问题，只需在本模型基础上，增设约束条件，使用 Matlab 代码求解即可。

十、参考文献

【1】qibbxxt.建模训练案例-3：有瓶颈设备多级生产计划问题中的复杂约束.

https://www.ilovematlab.cn/thread-610250-1-1.html(出处: MATLAB 中文论坛)

2022 年 8 月 6 日午 12 时

【2】盛骤，谢式千，潘承毅.概率论与数理统计-第四版.北京.高等教育出版社.2008 年

6 月（2018 年 6 月重印）

【3】司守奎，孙玺菁.数学建模算法与应用-第三版.北京.国防工业出版社.2022 年 2 月

重印