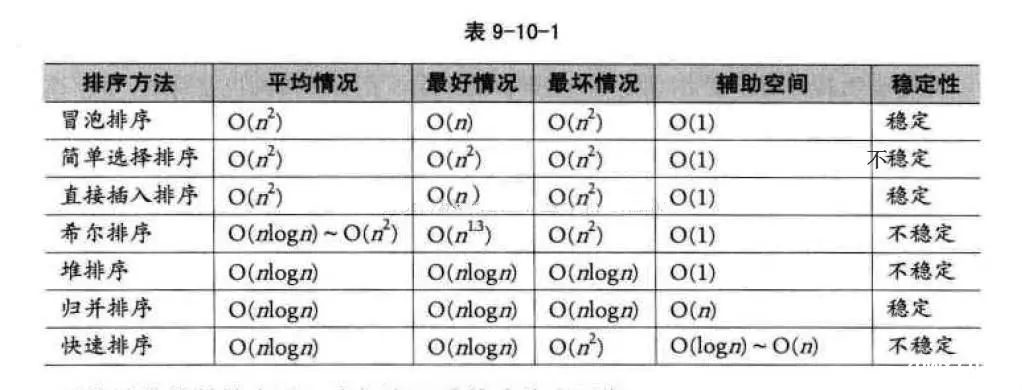
冒泡排序

冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

1.1 算法描述

<li>比较相邻的元素。如果第一个比第二个大，就交换它们两个；
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
• 针对所有的元素重复以上的步骤，除了最后一个；
• 重复步骤1~3，直到排序完成。

1.2 动图演示

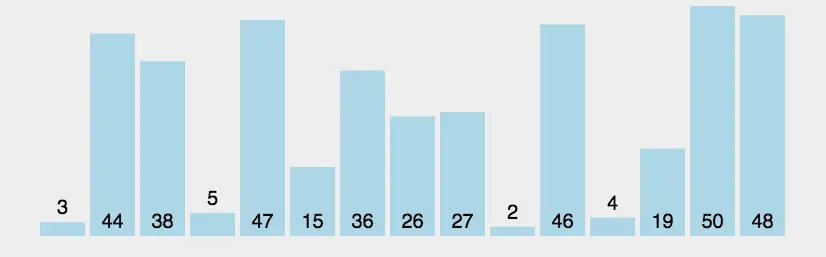
选择排序

在长度为N的无序数组中，第一次遍历n-1个数，找到最小的数值与第一个元素交换；

第二次遍历n-2个数，找到最小的数值与第二个元素交换；

。。。

第n-1次遍历，找到最小的数值与第n-1个元素交换，排序完成。

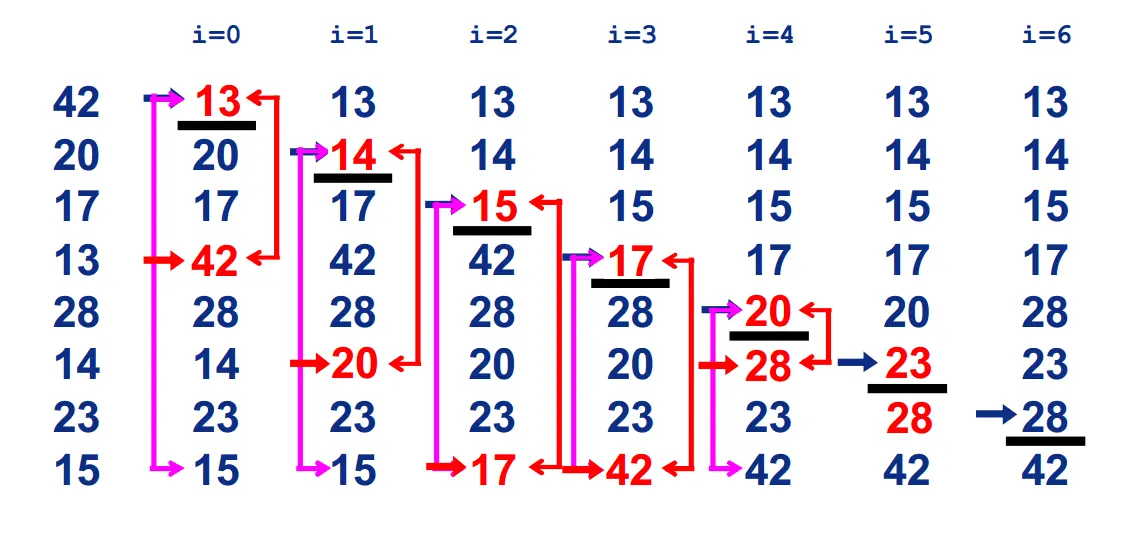
插入排序

在要排序的一组数中，假定前n-1个数已经排好序，现在将第n个数插到前面的有序数列中，使得这n个数也是排好顺序的。如此反复循环，直到全部排好顺序。

对于未排序数据(右手抓到的牌)，在已排序序列(左手已经排好序的手牌)中从后向前扫描，找到相应位置并插入。

插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

具体算法描述如下：

<li>从第一个元素开始，该元素可以认为已经被排序
1. 取出下一个元素，在已经排序的元素序列中从后向前扫描
2. 如果该元素（已排序）大于新元素，将该元素移到下一位置
3. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
4. 将新元素插入到该位置后
5. 重复步骤2~5

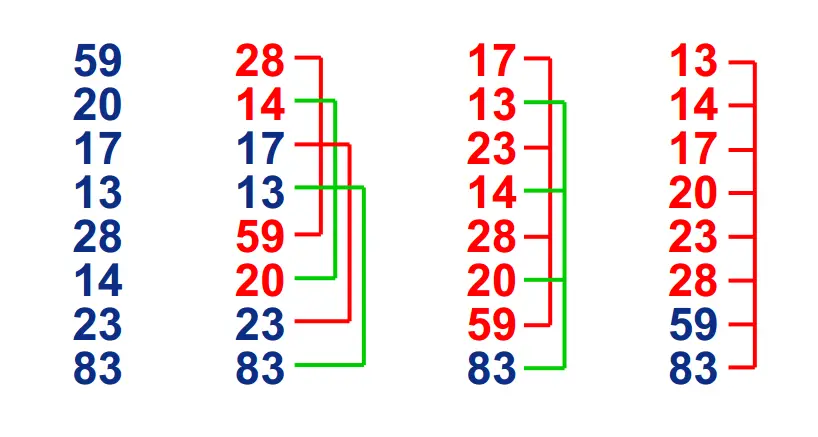
希尔排序

数据序列1： 13-17-20-42-28 利用插入排序，13-17-20-28-42. Number of swap:1;

数据序列2： 13-17-20-42-14 利用插入排序，13-14-17-20-42. Number of swap:3;

如果数据序列基本有序，使用插入排序会更加高效。

在要排序的一组数中，根据某一增量分为若干子序列，并对子序列分别进行插入排序。

然后逐渐将增量减小,并重复上述过程。直至增量为1,此时数据序列基本有序,最后进行插入排序。

堆排序

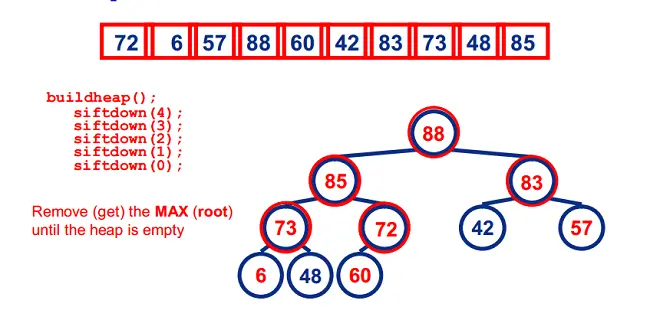
堆排序是指利用堆这种数据结构所设计的一种选择排序算法。堆是一种近似完全二叉树的结构（通常堆是通过一维数组来实现的），并满足性质：以最大堆（也叫大根堆、大顶堆）为例，其中父结点的值总是大于它的孩子节点。

我们可以很容易的定义堆排序的过程：

<li>由输入的无序数组构造一个最大堆，作为初始的无序区
1. 把堆顶元素（最大值）和堆尾元素互换
2. 把堆（无序区）的尺寸缩小1，并调用heapify(A, 0)从新的堆顶元素开始进行堆调整
3. 重复步骤2，直到堆的尺寸为1

   

   

   li>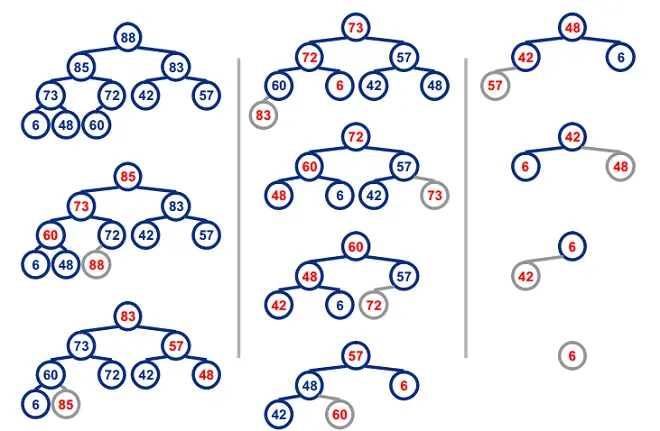

归并排序

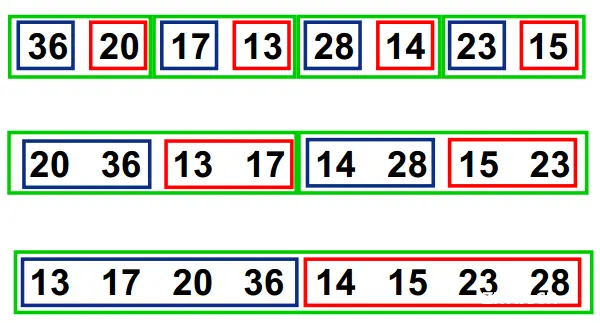
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用。

首先考虑下如何将2个有序数列合并。这个非常简单，只要从比较2个数列的第一个数，谁小就先取谁，取了后就在对应数列中删除这个数。然后再进行比较，如果有数列为空，那直接将另一个数列的数据依次取出即可。

快速排序

快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下，排序n个元素要O(nlogn)次比较。在最坏状况下则需要O(n^2)次比较，但这种状况并不常见。事实上，快速排序通常明显比其他O(nlogn)算法更快，因为它的内部循环可以在大部分的架构上很有效率地被实现出来。

快速排序使用分治策略(Divide and Conquer)来把一个序列分为两个子序列。步骤为：

<li>从序列中挑出一个元素，作为"基准"(pivot).
1. 把所有比基准值小的元素放在基准前面，所有比基准值大的元素放在基准的后面（相同的数可以到任一边），这个称为分区(partition)操作。
2. 对每个分区递归地进行步骤1~2，递归的结束条件是序列的大小是0或1，这时整体已经被排好序了。