参考：

算法学习笔记(5)：匈牙利算法漫谈匈牙利算法匈牙利算法、KM算法匈牙利算法（二分图）通俗易懂小白入门）二分图最大匹配——匈牙利算法多目标跟踪之数据关联（匈牙利匹配算法和KM算法）【小白学习笔记】（一）目标跟踪-匈牙利匹配

一、匈牙利算法基本概念

匈牙利算法（Hungarian algorithm），即图论中寻找最大匹配的算法，暂不考虑加权的最大匹配（用KM算法实现）。匈牙利算法（Hungarian algorithm），主要用于解决一些与二分图匹配有关的问题。

1. 二分图

二分图是图论中的一种特殊模型。若能将无向图G=(V,E)的顶点V划分为两个交集为空的顶点集，并且任意边的两个端点都分属于两个集合，则称图G为一个为二分图。二分图（Bipartite graph）是一类特殊的图，它可以被划分为两个部分，每个部分内的点互不相连。下图是典型的二分图。

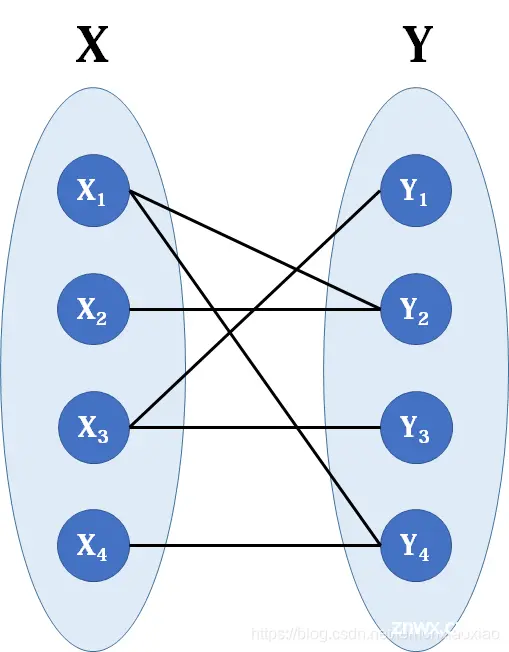
可以看到，在上面的二分图中，每条边的端点都分别处于点集X和Y中。

2. 匹配

图G的一个匹配是由一组没有公共端点的不是圈的边构成的集合。

这里，我们用一个图来表示下匹配的概念：

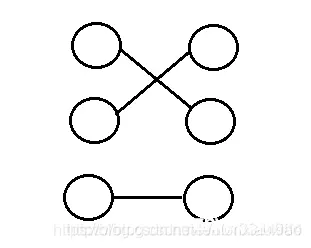
如图所示，其中的三条边即该图的一个匹配。所以，匹配的两个重点：1. 匹配是边的集合；2. 在该集合中，任意两条边不能有共同的顶点。

那么，我们自然而然就会有一个想法，一个图会有多少匹配？有没有最大的匹配（即边最多的匹配呢）？

3. 最大匹配

选择这样的边数最大的子集称为图的最大匹配问题。最大匹配的边数称为最大匹配。

4. 完美匹配

如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完美匹配（完全匹配），也称作完备匹配。考虑部集为X={x1 ,x2, …}和Y={y1, y2, …}的二分图，一个完美匹配就是定义从X-Y的一个双射，依次为x1, x2, … xn找到配对的顶点，最后能够得到 n！个完美匹配。

5. 最优匹配

最优匹配又称为带权最大匹配，是指在带有权值边的二分图中，求一个匹配使得匹配边上的权值和最大。一般X和Y集合顶点个数相同，最优匹配也是一个完备匹配，即每个顶点都被匹配。如果个数不相等，可以通过补点加0边实现转化。一般使用KM算法解决该问题。

6. 最小覆盖

二分图的最小覆盖分为最小顶点覆盖和最小路径覆盖：

①最小顶点覆盖是指最少的顶点数使得二分图G中的每条边都至少与其中一个点相关联，二分图的最小顶点覆盖数=二分图的最大匹配数；

②最小路径覆盖也称为最小边覆盖，是指用尽量少的不相交简单路径覆盖二分图中的所有顶点。二分图的最小路径覆盖数=|V|-二分图的最大匹配数；

7. 最大独立集

最大独立集是指寻找一个点集，使得其中任意两点在图中无对应边。对于一般图来说，最大独立集是一个NP完全问题，对于二分图来说：最大独立集=|V|-二分图的最大匹配数。

8. 交替路

从未匹配点出发，依次经过未匹配的边和已匹配的边，即为交替路，如Fig.3：3 -> 5 -> 1 -> 7 -> 4 -> 8

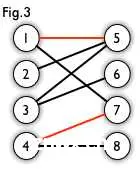
9. 增广路（也称增广轨或交错轨）

如果交替路经过除出发点外的另一个未匹配点，则这条交替路称为增广路，如交替路概念的例子，其途径点8，即为增广路。

由增广路的定义推出下面三个结论（设P为一条增广路）：

1). P的路径长度一定为奇数，第一条边和最后一条边都是未匹配的边（根据要途经已匹配的边和要经过另一个未匹配点，这个结论可以理解成第一个点和最后一个点都是未匹配点，可以在Fig.3上的增广路观察到）

2).对增广路径编号，所有奇数的边都不在M中，偶数边在M中。

3). P经过取反操作可以得到一个更大的匹配图，比原来匹配多一个（取反操作即，未匹配的边变成匹配的边，匹配的边变成未匹配的边，这个结论根据结论1).和交替路概念可得该结论）

4). 当且仅当不存在关于图M的增广路径，则图M为最大匹配。所以匈牙利算法的思路就是：不停找增广路，并增加匹配的个数。

二、匈牙利算法概述

匈牙利算法主要用来解决两个问题：求二分图的最大匹配数和最小点覆盖数。

1. 最大匹配问题

看完上面讲的，相信读者会觉得云里雾里的：这是啥？这有啥用？所以我们把这张二分图稍微做点手脚，变成下面这样：

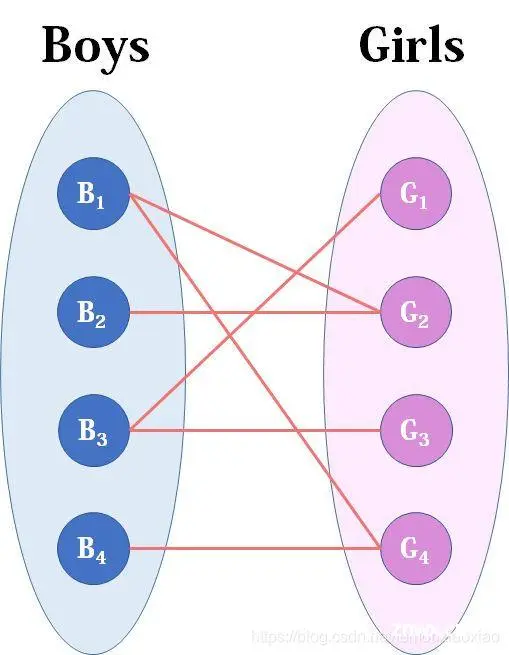
现在Boys和Girls分别是两个点集，里面的点分别是男生和女生，边表示他们之间存在“暧昧关系"。最大匹配问题相当于，假如你是红娘，可以撮合任何一对有暧昧关系的男女，那么你最多能成全多少对情侣？（数学表述：在二分图中最多能找到多少条没有公共端点的边）现在我们来看看匈牙利算法是怎么运作的：

我们从B1看起（男女平等，从女生这边看起也是可以的），他与G2有暧昧，那我们就先暂时把他与G2连接（注意这时只是你作为一个红娘在纸上构想，你没有真正行动，此时的安排都是暂时的）。

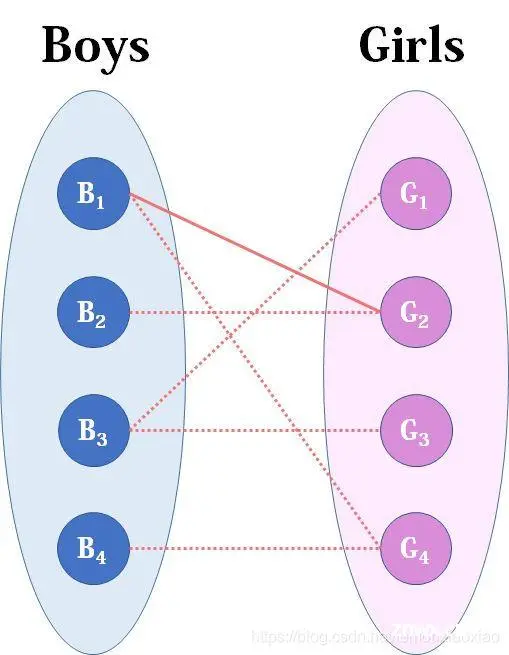
来看B2，B2也喜欢G2，这时G2已经“名花有主”了（虽然只是我们设想的），那怎么办呢？我们倒回去看G2目前被安排的男友，是B1，B1有没有别的选项呢？有，G4，G4还没有被安排，那我们就给B1安排上G4。

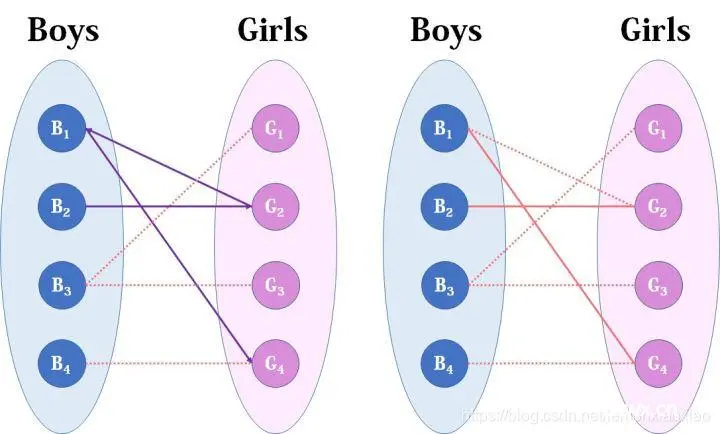
然后B3，B3直接配上G1就好了，这没什么问题。至于B4，他只钟情于G4，G4目前配的是B1。B1除了G4还可以选G2，但是呢，如果B1选了G2，G2的原配B2就没得选了。我们绕了一大圈，发现B4只能注定单身了，可怜。（其实从来没被考虑过的G3更可怜）

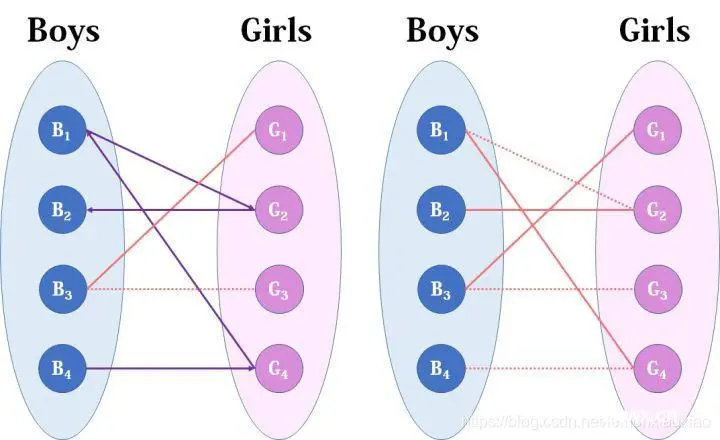
这就是匈牙利算法的流程，至于具体实现，我们来看看代码：

<code>int M, N; //M, N分别表示左、右侧集合的元素数量

int Map[MAXM][MAXN]; //邻接矩阵存图

int p[MAXN]; //记录当前右侧元素所对应的左侧元素

bool vis[MAXN]; //记录右侧元素是否已被访问过

bool match(int i)

{ -- -->

for (int j = 1; j <= N; ++j)

if (Map[i][j] && !vis[j]) //有边且未访问

{

vis[j] = true; //记录状态为访问过

if (p[j] == 0 || match(p[j])) //如果暂无匹配，或者原来匹配的左侧元素可以找到新的匹配

{

p[j] = i; //当前左侧元素成为当前右侧元素的新匹配

return true; //返回匹配成功

}

}

return false; //循环结束，仍未找到匹配，返回匹配失败

}

int Hungarian()

{

int cnt = 0;

for (int i = 1; i <= M; ++i)

{

memset(vis, 0, sizeof(vis)); //重置vis数组

if (match(i))

cnt++;

}

return cnt;

}

其实流程跟我们上面描述的是一致的。注意这里使用了一个递归的技巧，我们不断往下递归，尝试寻找合适的匹配。

注意：完美匹配一定是最大匹配，而最大匹配不一定是完美匹配。

2. 最小点覆盖问题

另外一个关于二分图的问题是求最小点覆盖：我们想找到最少的一些点，使二分图所有的边都至少有一个端点在这些点之中。倒过来说就是，删除包含这些点的边，可以删掉所有边。

这为什么用匈牙利算法可以解决呢？你如果以为我要长篇大论很久就错了，我们只需要一个定理：

一个二分图中的最大匹配数等于这个图中的最小点覆盖数。

三、匈牙利算法核心

匈牙利算法的核心就是不停的寻找增广路径来扩充匹配集合M。

我们给出实例来理解。

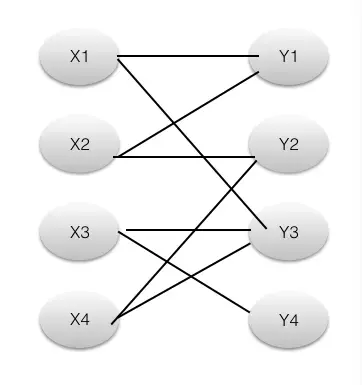
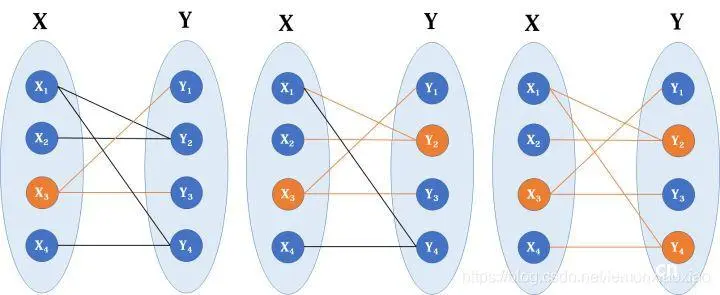
我们寻找如上图的最大匹配。

（1）首先M集合为空（即没有边在里面），然后开始从X1寻找增广路，遵循上述原则我们只能在Yi中找，找到Y1，（X1，Y1 ）这条路径，满足条件，取反，将（X1，Y1 ）这条路径加入到M中。

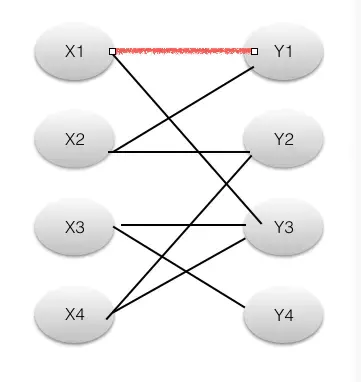
（2）接着，我们找到X2点。遵循原则，找到Y1，Y1不是未覆盖点，这个时候我们有两种选择，一个是深度搜索，一个是广度搜索，我们采用深度优先，虽然Y1不是未覆盖点，（X2,Y1）不是增广路，但是Y1连着X1，X1又和Y3相连，我们考虑（ X2,Y1,X1,Y3 ）这条路径，奇数？左右交替？起终点未覆盖？奇路径不属于M偶路径属于？满足所有增广路条件，所以这是一条增广路径，然后取反，得到如下图。

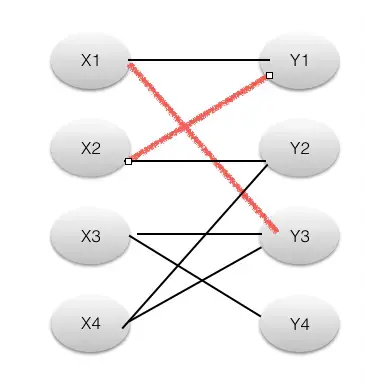
（3）现在M集合中的路径有两条了，由于我们找到了增广路径，使得M中的边数量增加。所以增广路径是匈牙利算法的核心，每找到一条增广路径，意味这M集合中边的数量就会增加1，当找不到增广路径的时候，这个时候M中边的数量就是我们二部图的最大匹配数量。

我们是怎样找到这条路径的呢，从X2开始寻找，我们先找到Y1，Y1不是未覆盖点，我们考虑Y1的原有匹配点X1，从X1开始寻找增广路，找到了Y3，当X1有增广路的时候，那么加上(X1,Y1)(X2,Y1)这两条路经，依然满足增广路条件。

所以基于我们上面的理解可以给出寻找增广路的伪代码：

<code> while(找到Xi的关联顶点Yj){ -- -->

if(顶点Yj不在增广路径上){

将Yj加入增广路

if(Yj是未覆盖点或者Yj的原匹配点Xk能找到增广路径){ //扩充集合M

将Yj的匹配点改为Xi;

返回true

}

}

返回false

}

从X2开始寻找是基于深度优先的，如果是基于广度优先呢？那么X2就会找到Y2。

四、匈牙利算法实现

深度优先匈牙利算法C语言代码：

typedef struct tagMaxMatch{

int edge[COUNT][COUNT];

bool on_path[COUNT];

int path[COUNT];

int max_match;

}GRAPH_MATCH;

void outputRes(int *path){

for (int i = 0 ; i<COUNT; i++) {

printf("%d****%d\n",i,*(path+i)); //Yj在前 Xi在后

}

}

void clearOnPathSign(GRAPH_MATCH *match){

for (int j = 0 ; j < COUNT ; j++) {

match->on_path[j] = false;

}

}

//dfs算法

bool FindAugPath(GRAPH_MATCH *match , int xi){

for (int yj = 0 ; yj < COUNT; yj++) {

if ( match->edge[xi][yj] == 1 && !match->on_path[yj]) { //如果yi和xi相连且yi没有在已经存在的增广路经上

match->on_path[yj] = true;

if (match->path[yj] == -1 || FindAugPath(match,match->path[yj])) { // 如果是yi是一个未覆盖点或者和yi相连的xk点能找到增广路经，

match->path[yj] = xi; //yj点加入路径;

return true;

}

}

}

return false;

}

void Hungary_match(GRAPH_MATCH *match){

for (int xi = 0; xi<COUNT ; xi++) {

FindAugPath(match, xi);

clearOnPathSign(match);

}

outputRes(match->path);

}

int main() {

GRAPH_MATCH *graph = (GRAPH_MATCH *)malloc(sizeof(GRAPH_MATCH));

for (int i = 0 ; i < COUNT ; i++) {

for (int j = 0 ; j < COUNT ; j++) {

graph->edge[i][j] = 0;

}

}

graph->edge[0][1] = 1;

graph->edge[0][0] = 1;

graph->edge[1][1] = 1;

graph->edge[1][2] = 1;

graph->edge[2][1] = 1;

graph->edge[2][0] = 1;

graph->edge[3][2] = 1;

for (int j = 0 ; j < COUNT ; j++) {

graph->path[j] = -1;

graph->on_path[j] = false;

}

Hungary_match(graph);

}