118. 杨辉三角

思路： 

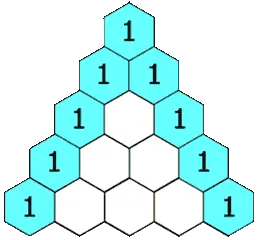
杨辉三角有以下性质使我们要用到的： 

● 每行数字左右对称，由 1 开始逐渐变大再变小，并最终回到 1。

● 第 n 行（从 0 开始编号）的数字有 n+1 项，前 n 行共有 2n(n+1)个数。

● 每个数字等于上一行的左右两个数字之和，可用此性质写出整个杨辉三角。即第 n 行的第 i 个数等于第 n−1 行的第 i−1 个数和第 i 个数之和。

代码：

<code>class Solution {

public:

vector<vector<int>> generate(int numRows) {

vector<vector<int>> vv(numRows);// 二维数组

for(int i = 0;i < numRows;i++)

{

vv[i].resize(i+1,1);// 按行数缩减每一行个数，并全部赋值为1

}

for(int a = 2;a < numRows ;++a)

{

for(int b = 1;b < a ;++b)

{ // 每个数是左上方和右上方之和

vv[a][b] = vv[a-1][b] + vv[a-1][b-1];

}

}

return vv;

}

};

260. 只出现一次的数字 III

思路：

1、相同数异或结果是0

假设数组 nums 中只出现一次的元素分别是 x1和 x2。如果把 nums 中的所有元素全部异或起来，得到结果 x，那么一定有：x = x1 ^ x2 。这是因为 nums 中出现两次的元素都会因为异或运算的性质 a ^ b ^ b = a 抵消掉，那么最终的结果就只剩下 x1和 x2的异或和。

2、区分两个单值数字到两个数组 

在异或操作中，只有当两个数字在某一位置上的二进制值不同，结果的该位置才会是1。因此，异或结果中为1的位表示了所有数字在该位上的差异。找到最后一个1的位，可以帮助我们区分数组中只出现一次的数字。通过最后一个1的位，我们可以将数组中的数字分成两组：一组在该位上为1，另一组在该位上为0。这两组数字在该位上的差异表明，至少有一个只出现一次的数字在该位上与其他数字不同。

3、找出异或值最后一个二进制为1的位置 

<code>a & (-a) 可以获得a最低的非0位，但需要注意整形溢出，可以用unsigned int 类型接收。

▶ 例如： 

● a的二进制原码是 0000 1010，这里最低非0位是从右往左第2位。

● -a在二进制中的表示是补码形式，即先按位取反再加1，取反得 1111 0101(反码)，加1得 1111 0110(补码)。

● 原码(0000 1010) 与 补码(1111 0110) 做与运算(&)，得 0000 0010，即原码 0000 1010的LSB（最低有效位）

---

▶ 我们发现： 

● 原码最低非0位右边所有的0，经由取反后全部变为1，反码+1会导致这些1逐位发生进位并变为0，最终进位记到最低非0位

● 原最低非0位是1，取反后是0，进位到这一位0变成1，不再向左进位

● 原最低非0位左边的每一位经由取反后 和 原码 进行与运算必为0

4、处理这两个数组

对于提供的整数数组的其他数，相同的数在所找到的mask位置的二进制数肯定是相同的，所以会被分到同一个数组。分别对两个数组进行异或操作就能得到最终两个单值。

代码：

class Solution {

public:

vector<int> singleNumber(vector<int>& nums) {

//取反操作就会在无符号整数的范围内进行,

//对-2,147,483,648 这个最小值取反时，会超出了int类型能表示的范围

unsigned int xornum = 0;

// 全部异或，相同的数会被异或成0

for (int n : nums) {

xornum ^= n;

}

// mask掩码：找出异或值最后一个二进制为1的数字 (重要位置)

int mask = xornum & (-xornum);

// 使用 vector 来存储结果

vector<int> res(2, 0);

// 如果要用数组存储，最后返回值要写改成vector ：

//int res[2] = {0, 0};

...

//return vector<int> {res[0],res[1]};

for (int n : nums) {

if ((n & mask) == 0) {

// 重要位置的数字是0，放在数组中全部异或，会剩下一个单值

res[0] ^= n;

} else {

// 重要位置的数字是1，放在数组中全部异或，会剩下另一个单值

res[1] ^= n;

}

}

return res;

}

};

137. 只出现一次的数字 II

思路：

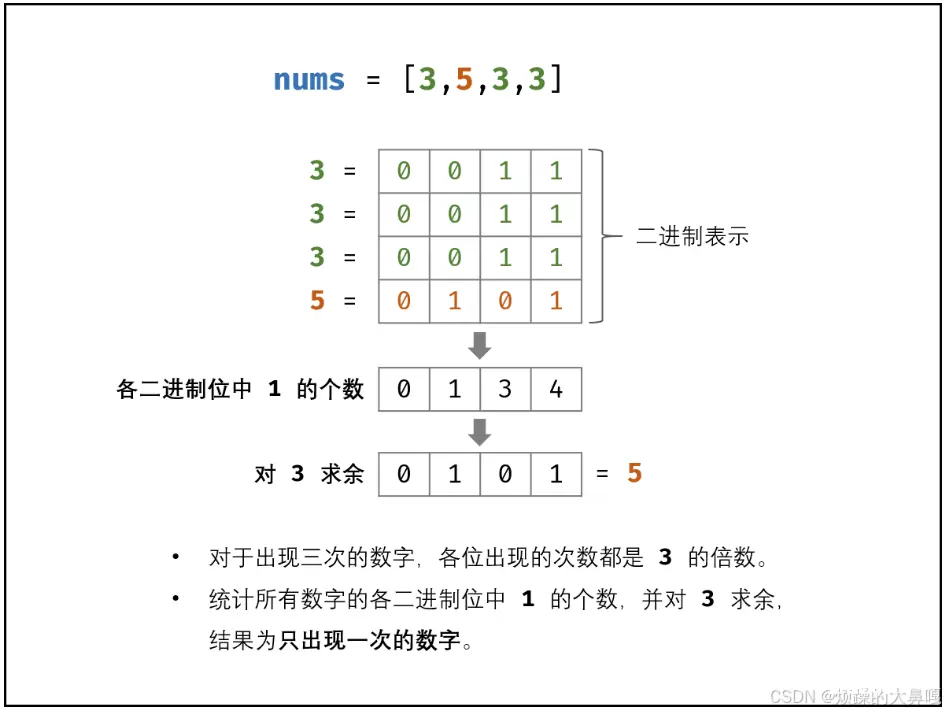
考虑数字的二进制形式，对于出现三次的数字，各二进制位出现的次数都是3的倍数。因此，统计所有数字的各二进制位中1的出现次数，并对3求余，结果为出现一次的数字。

方法：遍历统计

● 使用与运算，可获取二进制数字n的最右一位n1: n1 = n&i

● 配合右移操作，可获取n的所有为的值：n = n >> 1

● 建立一个32位的数组counts，通过以上方法可记录所有数字的各二进制位的 1 的出现次数

<code>int[] counts = new int[32];

for(int i = 0; i < nums.length; i++) {

for(int j = 0; j < 32; j++) {

counts[j] += nums[i] & 1; // 更新第 j 位

nums[i] >>= 1; // 第 j 位 --> 第 j + 1 位

}

}

● 将counts各元素对3求余，成三出现的数字在%3操作后没有余数，则结果为“只出现一次的数字”的二进制位。

for(int i = 0; i < 32; i++) {

counts[i] %= 3; // 得到 只出现一次的数字 的第 (31 - i) 位

}

● 利用左移操作和或运算，可将counts数组中个二进制位的值恢复到数字res上。

for(int i = 0; i < counts.length; i++) {

res <<= 1; // 左移 1 位

res |= counts[31 - i]; // 恢复第 i 位的值到 res

}

代码：

class Solution {

public:

int singleNumber(vector<int>& nums) {

vector<int> counts(32,0);

for(int n : nums)

{

for(int j = 0;j < 32 ; j++)

{

//n的最低位是0，那么n&1的结果是0

//n的最低位是1，那么n&1的结果是1

counts[j] += n & 1;//统计该位二进制数是1的个数

//>>> 是一个无符号右移操作符，与有符号右移操作符 >> 不同的是，

//无符号右移不考虑符号位，无论 num 是正数还是负数，左边空出的位都填充 0。

n >>= 1;//从右向左依次取二进制数

}

}

//成三出现的数字在%3操作后没有余数，只留下那个只出现一次的数字的二进制表示

for(int i = 0;i < 32;i++)

{

counts[i] %= 3;

}

int res = 0;

for(int i = 0;i < 32;i++)

{

//左移：最右边空出的位会被填充为0（无符号数）或保持符号位的值（有符号数）

res <<= 1;

res |= counts[31 - i];//或运算：比较的位中至少有一个为1，则结果位为1

// 这里是31 - i，要注意二进制数存储的先后

}

return res;

}

};

26. 删除有序数组中的重复项

左右指针即可！

代码： 

<code>class Solution {

public:

int removeDuplicates(vector<int>& nums) {

if(nums.size() == 0)

return 0;

int left = 1,right = 1;

while(right < nums.size())

{

if(nums[right] != nums[right-1])

{

nums[left++] = nums[right];

}

++right;

}

return left;

}

};

JZ39 数组中出现次数超过一半的数字

数组中出现次数超过一半的数字_牛客题霸_牛客网

思路：

用计数排序的思想，numbers数组的值与counts数组下标相同时对counts[ ]进行计数，最后将存储的计数与原数组长度的一半进行对比。

 注意这里创建新数组要开辟动态的，根据所给数组的最大值进行创建。

代码：

<code>#include <algorithm>

class Solution {

public:

int MoreThanHalfNum_Solution(vector<int>& numbers) {

if (numbers.empty())

return 0;

//动态数组

int maxnum = 0;

for(int m : numbers)

{// 找到数组中的最大值

maxnum = max(maxnum,m);

}

//初始化数组

vector<int> counts(maxnum + 1,0);

for(int i :numbers)

{// 计数

counts[i]++;

}

for(int j = 0; j < counts.size();j++)

{

if(counts[j] > numbers.size()/2)

{

return j;

}

}

return 0;

}

};

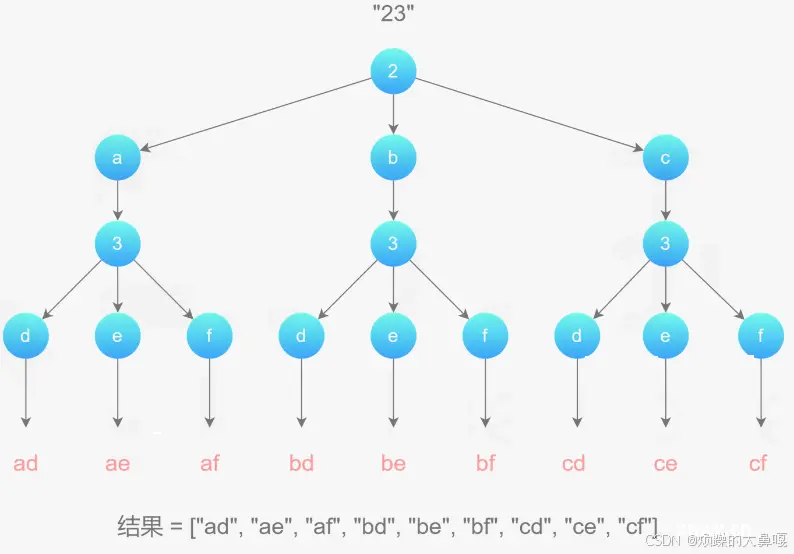
17. 电话号码的字母组合（666）

思路： 

对于示例1，我们利用树的形式表示出来，但实现这个过程要用到递归的思想​​​​​​​。

维护一个字符串，表示已有的字母排列，该字符串初始为空。每次取电话号码的一位数字，从字符串数组中获得该数字对应的所有可能的字母，并将其中的一个字母插入到已有的字母排列后面。（即一个一个取第一个号码对应的字母，并与另一个号码对应字母一个一个结合）然后继续处理电话号码的后一位数字，直到处理完电话号码中的所有数字。

代码： 

<code>class Solution {

string Number[10] = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};

//深度优先遍历,递归实现,像树一样往深找

void dfs(int i,int len, string digits,string& path,vector<string>& ans)

{

if(i == len)

{//直到找到所有组合

ans.push_back(path);//两两组合后尾插到动态数组

return;

}

for(auto e : Number[digits[i] - '0'])//根据下标找到对应数字的字符串

{

path[i] = e;

dfs(i+1,len,digits,path,ans);//注意这里是+1，不是++，用来维护一个字符串

}

}

public:

vector<string> letterCombinations(string digits) {

int len = digits.length();

if(len == 0)

return {};

vector<string> ans;

string path(len,0);

dfs(0,len,digits,path,ans);

return ans;

}

};

 这一篇写了好久~  (ಥ﹏ಥ)  (ಥ﹏ಥ)  (ಥ﹏ಥ)