㗅是一种享受。

搚是一种酷刑！

享受健康人生。

开启口胡生活！

¿ 如何 搞笑 高效做题 ?

只需要口胡CF题就行啦！（

从今天起口胡 CF 按照洛谷通过人数排序的题单

从 CF2000 Part 1 开始

CF24E XOR on Segment

<li>给定 \(n\) 个数的序列 \(a\)。\(m\) 次操作，操作有两种：
1. 求 \(\displaystyle\sum_{i=l}^r a_i\)。
2. 把 \(a_l\sim a_r\) 异或上 \(x\)。
• \(1\le n\le 10^5\)，\(1\le m\le 5\times 10^4\)，\(0\le a_i\le 10^6\)，\(1\le x\le 10^6\)。

思路：开 \(\log(A)\) 个线段树记录二进制下每一位是 \(0\) 还是 \(1\)。 \(A\) 代表值域。空间 \(T(2n\log(A))\) ，时间 \(T(n\log(n)\log(A))\)

CF1200E Compress Words

• Amugae 有 \(n\) 个单词，他想把这个 \(n\) 个单词变成一个句子，具体来说就是从左到右依次把两个单词合并成一个单词。合并两个单词的时候，要找到最大的 \(i(i\ge 0)\)，满足第一个单词的长度为 \(i\) 的后缀和第二个单词长度为 \(i\) 的前缀相等，然后把第二个单词第 \(i\) 位以后的部分接到第一个单词后面。输出最后那个单词。

不就是 kmp 裸题吗，过。

等等，我看题解好像有诈。我写一写代码

废了，写了四遍还没过

突然看到题解的一句话：

<code>首先，这题要先注意题面。如果你把合并单词的过程理解成“单词与单词合并”，你就会被 test 4 卡掉。【调了很久才发现】

正确的理解方式是：“单词与合并完成的句子合并”

哦哦哦哦哦哦原来是这样我

那复杂度不就变成 \(O(n^2)\) 了吗？寄。

哦，原来新串和原串 getnxt 的时候只用加入与新串长度相等的原串就行了，复杂度 \(T(2n)\)

CF784E Twisted Circuit

<li>



li>
• 读入四个整数 \(0\) 或者 \(1\)，作为如图所示的电路图的输入。请输出按照电路图运算后的结果。

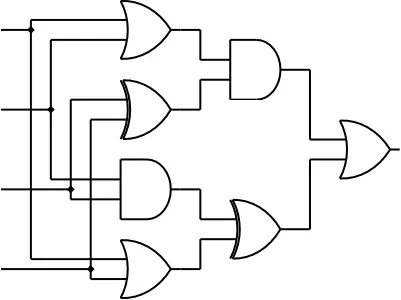
简单题，过。

CF235B Let's Play Osu!

• 一个 \(01\) 串，第 \(i\) 个字符有 \(p_i\) 的概率成为 \(0\) ， \(1-p_i\) 的概率成为 \(1\) ，求所有（【连续 \(0\) 的长度】的平方）之和的期望。 \(n \le 10^5\)

定义 \(f_i\) 代表第 \(i\) 位是 \(1\) 的时候已知的期望。那么有

\[\begin{align}

f_i&=\sum f_{j\in[0,i-1]}\cdot(i-j-1)^2\cdot\prod p_{k\in[j+1,i-1]}\cdot(1-p_i)\\

&=\sum\limits_{j=0}^{i-1}\prod\limits_{k=j+1}^{i-1} p_k\cdot(f_j\cdot j^2-2j\cdot f_j \cdot (i-1)+f_j \cdot (i-1)^2)

\end{align}

\]

只要记录 \(\displaystyle\sum f_j\cdot j^2\) 、\(\displaystyle\sum 2j\cdot f_j\)、\(\displaystyle\sum f_j\) ，每次乘上对应的系数就能 \(O(n)\) 转移了。

时间复杂度 \(O(n)\)

答案还有更奇妙的做法，我学习一下：

记录 \(k_i\) 代表 \(i\) 位置的期望连续 \(0\) 长度， \(f_i\) 代表 \(i\) 位置及以前的期望。

\(k_i=(k_{i-1}+1)\times p_i\)

\(f_i = f_{i01} \times (1-p_i) + (f_{i-1}+2 \times k_{i-1}+1)\times p_i\)

CF2B The least round way

• 上古题

• 以左上角为起点。
• 每次只能向右或向下走。
• 以右下角为终点。
• 如果我们把沿路遇到的数进行相乘，积应当以尽可能少的 \(0\) 结尾。

显然要么最小化 \(2\) 的数量，要么最小化 \(5\) 的数量。

记录 \(f^2_{x,y}\) 和 \(f^5_{x,y}\) ，答案就是 \(\min(f^2_{m,n},f^5_{m,n})\)。为什么处理 \(f^2\) 不用统计 \(5\) 的数量？ 因为如果 \(5\) 比 \(2\) 要少，那么 \(f^5\) 肯定会更优。所以 \(f^2\) 能成为答案就证明 \(2\) 不比 \(5\) 多。

做完……了吗？

注意，矩阵里面有 \(0\)

如果 \(\min(f^2,f^5) > 1\) ，就还要考虑经过 \(0\) 的情况。 而且 \(f^2\) 、 \(f^5\) 的统计也要避开 \(0\) 。

CF920F SUM and REPLACE

• 给定 \(n\) 个数的数组 \(a\)，\(m\) 次操作。操作有两种：
  1. 将 \(i\in[l,r]\) 中的所有 \(a_i\) 替换为 \(d(a_i)\)。\(d(x)\) 表示 \(x\) 的正约数的个数。
  2. 求 \(\displaystyle\sum_{i=l}^r a_i\)。
• \(1\le n,m\le 3\times 10^5\)，\(1\le a_i\le 10^6\)。

感觉一个数操作不了几次就会变 \(0\)。

所以对每个不是 \(1\) 的数暴力修改。查找不是 \(1\) 的数可以用线段树 \(O(n\log n)\)，可以用跳表 \(O(n+\log n)\)。 更好的做法是并查集，每个 \(1\) 的 fa 指向下一个未被修改的数。 复杂度 \(O(n\alpha)\)

如何求正因数个数？ \(O(A\log A)\) 向后更新预处理即可。

CF171E MYSTERIOUS LANGUAGE

<code> You are given a mysterious language (codenamed "Secret") available in "Custom Test" tab. Find out what this language is and write a program which outputs its name. Note that the program must be written in this language.

This program has only one test, and it's empty (it doesn't give your program anything to read).

Output the name of the mysterious language.

建议评黑！！！

CF383C Propagating tree

<li>

很久以前，有一棵神橡树(oak)，上面有\(n\)个节点，从\(1\)~\(n\)编号，由\(n-1\)条边相连。它的根是\(1\)号节点。

• 这棵橡树每个点都有一个权值，你需要完成这两种操作：

• \(1\) \(u\) \(val\) 表示给\(u\)节点的权值增加\(val\)

• \(2\) \(u\) 表示查询\(u\)节点的权值

• 但是这不是普通的橡树，它是神橡树。

• 所以它还有个神奇的性质：当某个节点的权值增加\(val\)时，它的子节点权值都增加\(-val\)，它子节点的子节点权值增加\(-(-val)\)...... 如此一直进行到树的底部。

给奇数深度和偶数深度，分别重链剖分、建线段树。每个询问就向上统计 \(val\) 的和。

复杂度 \(O(m\log n)\)

oh,原来还可以用树状数组做啊。 具体做法略了。

CF1132F Clear the String

• 给你一个串\(s\)，每次可以花费 \(1\) 的代价删去一个子串，要求子串的每一位为同一个字符。

• 求删去整个串的最小代价。

• \(1\le |s|\le 500\)

• 例如，abaca 就要删 \(3\) 次。

设 \(f_{i,c}\) 代表把 \([1,i]\) 变成只有 \(c\) 字符的代价。

\(f_{i,c}=f_{i-1,c'}+[c\not=c']+[c\not=s[i]]\)

这复杂度\(O(nZ^2)\)显然不对啊，我写一个对拍看看为啥。

Oh,这样就失去合并的顺序，只能正序合并。

那就设 \(f[l,r,0/1] \leftarrow f[l+1,r,0/1],f[l,r-1,0/1]\) ，其中 \(0/1\) 代表这个区间最后是 \(s[l]\) 还是 \(s[r]\) 的字符。

复杂度 \(O(n^2)\) ，感觉还是不太对，但是过样例了，写个对拍试试。

还是寄了。原来一个区间不止能变成两端的字符，也可以被统一成中间的字符。比如这组数据 abacbcc ，其中的 abacb 要被统一成 c 才行。

然后 TLE 了。突然我想到 \(f[l,r,c]\) ，不同 \(c\) 的 \(f\) 相差最多只有 \(1\) ，这启发我们记录最小的 \(c\) 是哪些。

然后就 AC 了。看看题解吧。

哦，原来我最开始的想法是对的。一个区间一定可以变成最左端的字符而最优。之前没 AC 是因为一个区间 \([l,r]\) 不一定由 \([l,l]+[l+1,r]\) 或 \([l,r-1]+[r,r]\) 合并而来。而是由 \([l,j]+[j+1,r]\) 合并而来。

CF895C Square Subsets

• 对于一些数组 \(a\)，Petya 需要找到从中间选择非空子集，使所有数的乘积为完全平方数的方法的数量。如果这些方法所选择的元素的索引不同，则认为这两种是不同的方法。 因为结果可能很大，结果需要 \(\bmod ~ 10^9+7\)。
• \(1 \le a_i \le 70\)

观察到值域 \(A\) 很小，考虑开个桶存所有 \(a_i\) 。同时发现只有 \(19\) 个质数，所以记录 \(f[i][...19维]\) 存储在 \(i\) 数值之前的每一个质因子的奇偶性。

对于每一个桶值 \(i\)， 更新 \(f\) ，答案就是 \(\displaystyle\sum f[i][000...000]\)

为什么题目标签里面有线性基？不明白，那就写一写代码吧。

就这么水灵灵地过啦？？！

为什么要线性基（不解）

看了看线性基的做法，太妙了。是先钦定 \(cnt\) 个元素构成完全平方数的基底，剩下的数就可以随便选了，答案是 \(2^{n-cnt}-1\)