文章目录

一、操作符的分类二、二进制和进制转换1.二进制与十进制的相互转换2,二进制与八进制的相互转换3.二进制与十六进制的相互转换

三、原码、反码和补码四、移位操作符1.左移操作符（1）左移操作符移位方法（2）左移操作符规律总结

2.右移操作符（1）逻辑右移移位方法（2）逻辑右移规律总结（3）算术右移移位方法（4）算术移位规律总结

五、位操作符：&、|、^、~1.按位与操作符&2.按位或操作符|3.按位异或^4.按位取反~

六、单目操作符

一、操作符的分类

操作符大致分类如下：

算术操作符： + 、- 、* 、/ 、%移位操作符: << >>位操作符: & | ^赋值操作符: = 、+= 、 -= 、 *= 、 /= 、%= 、<<= 、>>= 、&= 、|= 、^=单⽬操作符： ！、++、–、&、*、+、-、~ 、sizeof、(类型)关系操作符: > 、>= 、< 、<= 、 == 、 !=逻辑操作符： && 、||条件操作符： ? :逗号表达式： ,下标引⽤： []函数调⽤： ()结构成员访问： . 、->

上述的操作符，我们已经讲过算术操作符、赋值操作符、逻辑操作符、条件操作符和部分的单⽬操作符，今天继续介绍⼀部分，操作符中有⼀些操作符和⼆进制有关系，我们先铺垫⼀下⼆进制的和进制转换的知识

二、二进制和进制转换

其实我们经常能听到 2进制、8进制、10进制、16进制 这样的讲法，那是什么意思呢？

其实2进制、8进制、10进制、16进制是数值的不同表⽰形式⽽已，⽐如：数值15的各种进制的表⽰形式：

<code>15的2进制：1111

15的8进制：17

15的10进制：15

15的16进制：F

//16进制的数值之前写：0x

//8进制的数值之前写:0

我们重点介绍⼀下⼆进制：

⾸先我们还是得从10进制讲起，其实10进制是我们⽣活中经常使⽤的，我们已经形成了很多尝试：

• 10进制中满10进1

• 10进制的数字每⼀位都是0~9的数字组成

其实⼆进制也是⼀样的

• 2进制中满2进1

• 2进制的数字每⼀位都是0~1的数字组成

那么 1101 就是⼆进制的数字了

1.二进制与十进制的相互转换

二进制转为十进制：

其实10进制的123表⽰的值是⼀百⼆⼗三，为什么是这个值呢？其实10进制的每⼀位是有权重的，也称为位权，10进制的数字从右向左是个位、⼗位、百位…，分别每⼀位的权重是 10的零次方 , 10的一次方 , 10的二次方 …，整个求值过程如图：

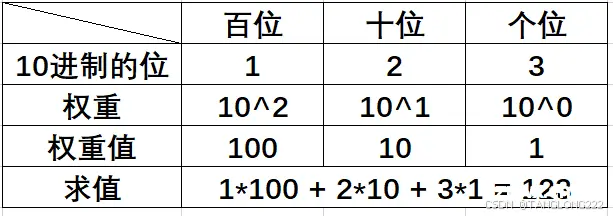
2进制和10进制是类似的，只不过2进制的每⼀位的权重，从右向左是: 2 , 2 , 2 … 0 1 2

如果是2进制的1101，该怎么理解呢? 如图：

这就是2进制转换为十进制的完整过程，只要记住每一位的权重，然后乘以对应位的值即可，最后得到的就是十进制，这个方法叫做按权展开相加法十进制转二进制：

如果有一个十进制数字150，我们怎样去得到它对应的二进制呢？这里我们要用到的方法就是除基取余倒排法，其中的基就是基数，多少进制，基数就是多少，如：2进制的基数就是2。

除基取余倒排法就用在十进制转为其它进制上，它的意思就是，用这个十进制数去除以另一个进制的基数，然后写出每次相除的余数，最后倒着排列，就得到了对应的进制数

比如十进制150转为二进制，用150除以2，然后记下余数，最后将所有余数倒着排列即可，具体方法如下：

2,二进制与八进制的相互转换

8进制的数字每⼀位是0 ~ 7的数字

二进制转为八进制：

二进制转为八进制非常简单，每三位为一组的二进制算出来，对应一位八进制，从右到左开始划分，如果划分到最左边时不够三位，那么就在前面补上对应的0，或者忽略掉也可以，把二进制01101011转换位十进制的方法如下：

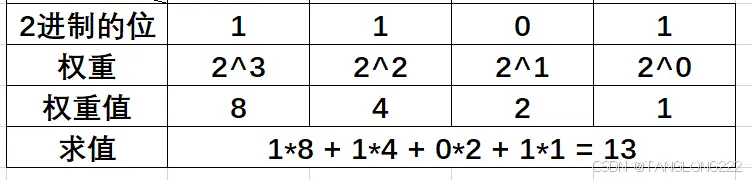
八进制转二进制：

八进制转二进制也很简单，只需要把每一位的八进制数字组合成三位二进制数字，如把八进制17转为二进制的方法就是，将1拆成3位二进制数，将7拆为3为二进制数，最后得到答案，如下：

3.二进制与十六进制的相互转换

16进制的数字每⼀位是0 ~ 9, a ~ f 中的一个，a ~ f代表10~15的数字

二进制转为十六进制：

与二进制转八进制相似，二进制转八进制就是每三位二进制为一位八进制，而二进制转十六进制就是每4位二进制转1位十六进制，二进制11010110转为十六进制的过程如下：

2, 十六进制转二进制：

也与八进制转二进制类似，十六进制转二进制就是每一位十六进制写成4位二进制的组合，如把十六进制12A转换为二进制的过程为：

三、原码、反码和补码

整数可以分为有符号整数和无符号整数，无符号整数就全部都是正数，而一般的原码、反码和补码一般出现在有符号整数中，在有符号整数中，数值的表⽰⽅法有三种，即原码、反码和补码

有符号整数的三种表⽰⽅法均由符号位和数值位两部分组成，2进制序列中，最⾼位的1位是被当做符号位，剩余的都是数值位，符号位都是⽤0表⽰“正”，⽤1表⽰“负”

正整数的原、反、补码都相同，负整数的三种表⽰⽅法各不相同，如下：

原码：直接将数值按照正负数的形式翻译成⼆进制得到的就是原码反码：将原码的符号位不变，其他位依次按位取反就可以得到反码，0变成1,1变成0补码：反码加一就得到补码，知道补码也可以求原码，只需要再对补码取反加一，就可以得到原码

对于整形来说：数据存放内存中其实存放的是补码，因为在计算机系统中，数值⼀律⽤补码来表⽰和存储。原因在于，使⽤补码，可以将符号位和数值位统⼀处理；同时，加法和减法也可以统⼀处理为加法（CPU只有加法器），此外，补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路

四、移位操作符

移位操作符分为左移操作符（<<）和右移操作符（>>），它的操作数只能是整数，只能移位正整数，如>>1，而不能>>-1，这是未定义的部分，不要使用，并且移位的对象是二进制，所以要对其它进制进行移位时，需要将其转化为二进制再进行移位

1.左移操作符

（1）左移操作符移位方法

规则：二进制向左边移动n位，移动后左边抛弃、右边补0，如图以下例子，它的运行结果是什么呢？

根据移位操作符的规则，如果是二进制，可以直接移位，如果不是二进制，将其转化为二进制之后进行移位，注意，计算机里面存储信息都是以补码的形式，所以转为二进制原码后还要转换为补码，这里的10很明显是十进制，所以我们要对它进行移位，就要先转化为二进制，由于int类型占用4个字节，也就是32位，所以十进制10转为二进制为：

<code>00000000 00000000 00000000 00001010

由于正数的原码就是它的补码，所以此时可以直接对它进行左移操作，相当于就是将整个数往左抬了一下，去掉了最左边的一位，然后再在最后补上0，如图所示：

也就是最后左移的结果为：

<code>00000000 00000000 00000000 00010100

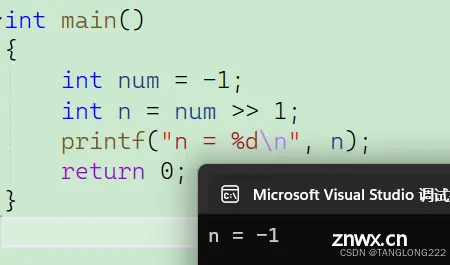
转换为十进制就是20，最后我们思考一下，n肯定就是20了，那num有没有更改呢？num是10还是20呢？我们来看看运行结果：

可以看到，num没有变化，因为n = num << 1 的含义是将num左移一位的结果赋值给n，并没有改变num的值，换个通俗的例子：n = num * 2，这里只是把num乘2的结果赋值给n，并没有改变num的值，如果要让num左移一位，应该写成num = num <<1，或者num <<= 1

（2）左移操作符规律总结

左移操作符对一个十进制整数的影响是有规律的，无论正负数，都可以对原数值起到乘以2的移位次方的作用，比如将10左移了1位，那么就对原数值乘以了2的一次方，变成了20，依次类推，如果是-10左移了1位，那么就会变成-20

2.右移操作符

右移操作符有点特殊，有两种，分为两种逻辑右移和算术右移两种，逻辑右移主要用于无符号数的位运算，而算术右移主要用于有符号数的位运算。 因为有符号数右移时需要考虑符号位的变化，而无符号数则没有符号位的问题，所以它们移位规则如下：

逻辑右移：二进制向右移动n位，右边抛弃，左边全部补0算术右移：二进制向右移动n位，右边抛弃，左边全部补符号位

（1）逻辑右移移位方法

类似于左移操作符，一般用于无符号数，将一个无符号二进制数向右移动n位，然后将右边抛弃，左边补0，比如将无符号数10右移一位，如图：

我们要对10进行逻辑右移操作，首先将它转为二进制，并且是内存中的补码，在上文中已经转换过一次了，这里直接给出结果：

<code>00000000 00000000 00000000 00010100

然后我们将这个二进制数向右抬一位，然后抛弃右边，然后在左边补0，就实现了逻辑右移，如图所示：

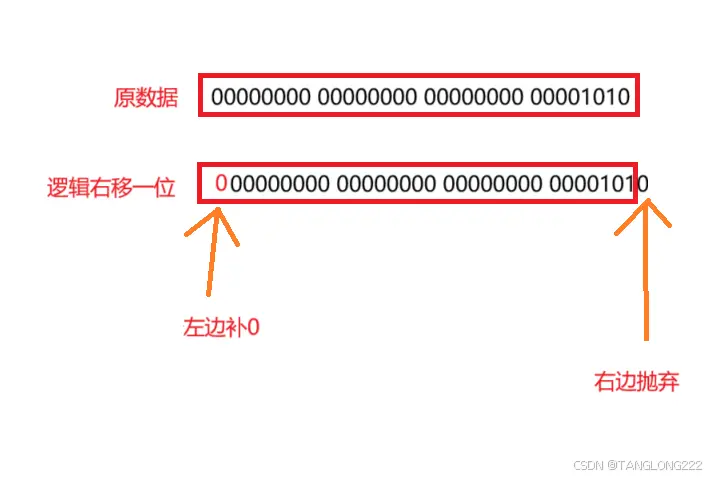
所以最后逻辑右移的结果为：

<code>00000000 00000000 00000000 00000101

转换为十进制就是5，运行结果如图：

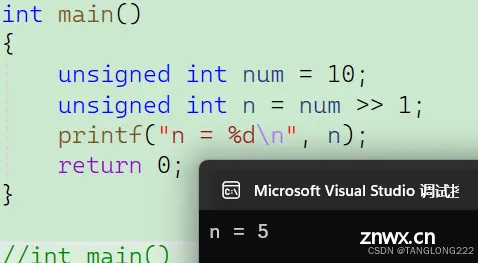
（2）逻辑右移规律总结

对一个无符号数进行右移操作，会对它进行除以2的移位次方，比如将10右移一位，就对它除以了2的一次方，最后变成了5，那如果这个数不是偶数怎么办呢？比如123向右移一位，它除以2就是61.5，最后结果会返回这个数两边较小的整数，61.5的两边分别是61和62，最终得到小的那个数61，所以综上，逻辑右移操作符对操作的数有除以2的移位次方的作用，如果不能整除，会返回这个数两边较小的整数

（3）算术右移移位方法

与逻辑右移不同，一般用于有符号数，将一个有符号二进制数向右移动n位，然后将右边抛弃，左边全部补符号位，如将有符号数-1右移一位，如图：

现在的-1是十进制，我们要将其转化为二进制，而且要注意，它是负数，在内存中存储的是它的补码，所以我们要将十进制数-1转为原码，然后除了符号位按位取反，最后+1得到补码，再对补码进行操作，如下：

<code>原码：10000000 00000000 00000000 00000001

反码：11111111 11111111 11111111 11111110

补码：11111111 11111111 11111111 11111111

最后我们得到了-1的补码为32个1，然后对它进行算术右移操作，将右边抛弃，左边补上符号位，如下图：

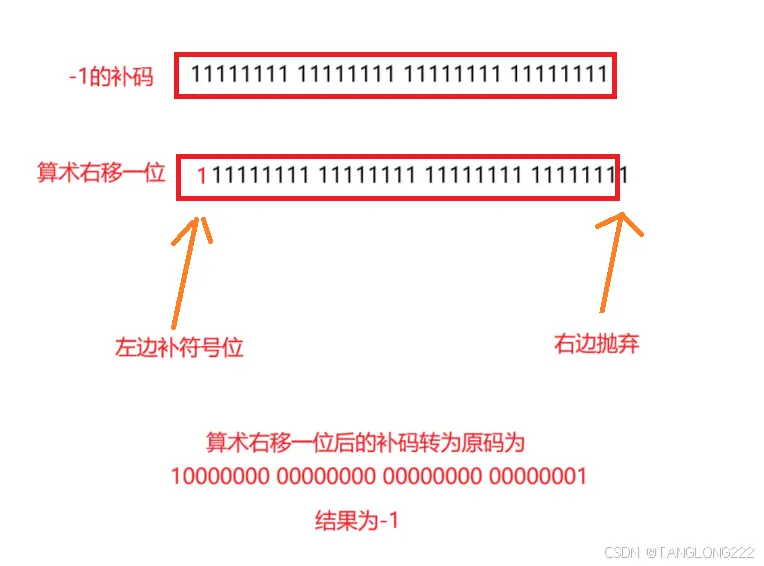
运行结果如图：

（4）算术移位规律总结

其实虽然算术右移和逻辑右移的用法不同，但是它们的效果都是一样的，算术右移也是会让原本的数除以2的位移次方，并且如果不能整除，会返回两边较小的整数，比如-1算术右移了1位，也就是除以了2，变成-0.5，-0.5两边的整数是0和-1，然后由于-1较小，所以最终结果就是-1

最后再次提醒，移位操作符只能对二进制移位，如果不是二进制，要转为二进制，并且转为对应的补码，再进行移位，并且只能移位正整数，不能负数，如<<-1，都是错误的写法，

五、位操作符：&、|、^、~

<code>& //按位与

| //按位或

^ //按位异或

~ //按位取反

需要注意的是前三个都是双目操作符，需要两个操作数，而最后一个按位取反是单目操作符，操作数只有一个

1.按位与操作符&

要与逻辑与操作符&&区分开，两个操作符的用法完全不同，逻辑与操作符在之前已经讲过，如果遗忘了可以自行去复习

按位与操作符也是针对二进制的，并且是一个数的补码，按位与的特点如下：

（1）0 & 0 = 0

（2）1 & 0 = 0

（3）0 & 1 = 0

（4）1 & 1 = 1

我们现在举例来进行说明，如下图：

由于按位与操作符是对二进制位进行与，所以我们先将它们转换为二进制的补码，过程如下：

<code>-3转换过程

原码：10000000 00000000 00000000 00000011

反码：11111111 11111111 11111111 11111100

补码：11111111 11111111 11111111 11111101

5转换过程：

由于正数的原码、反码和补码相同所以只需要求到原码即可

原码：00000000 00000000 00000000 00000101

接下来我们按照规则对它们进行按位与运算，如下：

-3: 11111111 11111111 11111111 11111101

5: 00000000 00000000 00000000 00000101

按位与: 00000000 00000000 00000000 00000101

最后我们可以看出得到的结果是一个正数，它的补码就是原码，所以只需要直接将其算出来，结果为5，运行结果如下：

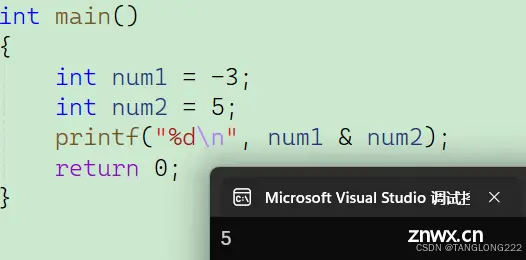
2.按位或操作符|

按位或操作符也要和逻辑或||进行区分，按位或也是针对与二进制的，它的规则如下：

<code>0 | 0 = 0

1 | 0 = 1

0 | 1 = 1

1 | 1 = 1

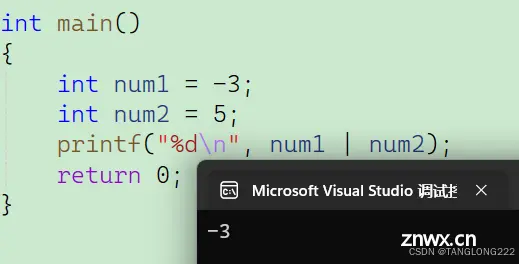
接下来我们还是举例说明，还是使用上面的那个数据，如图：

上面已经算过-3和5的补码，这里不再计算，直接给出它们按位或的过程：

<code>-3: 11111111 11111111 11111111 11111101

5: 00000000 00000000 00000000 00000101

按位或: 11111111 11111111 11111111 11111101

可以看到我们得出的结果应该是个负数，并且要注意这是负数的补码，必须转为原码才行，然后我们现在对它进行取反+1的操作，如下：

补码：11111111 11111111 11111111 11111101

取反：10000000 00000000 00000000 00000010

加一：10000000 00000000 00000000 00000011

最后我们可以看出结果应该是-3，运行结果如下：

3.按位异或^

按位异或的规则比较不同，就是：相异或的两个数不同则为真，也就是1，相同则为假，也就是0，如下：

<code>1 ^ 1 = 0

0 ^ 0 = 0

1 ^ 0 = 1

0 ^ 1 = 1

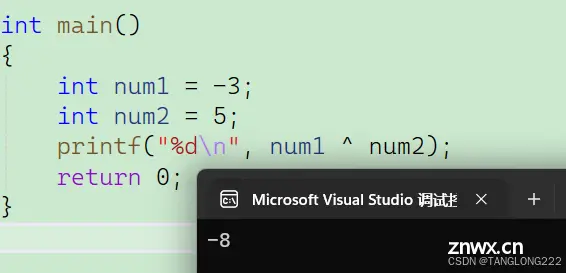
我们还是以上面的数据为例，代码如下：

接下来我们直接用上面算过的补码进行按位异或操作，如下：

<code>-3: 11111111 11111111 11111111 11111101

5: 00000000 00000000 00000000 00000101

异或: 11111111 11111111 11111111 11111000

我们注意到结果也是个负数，这是补码，要将其转为原码，如下：

补码：11111111 11111111 11111111 11111000

反码：10000000 00000000 00000000 00000111

加一：10000000 00000000 00000000 00001000

所以最后异或的答案为-8，我们来看看具体的运行结果：

4.按位取反~

按位取反就是原码变反码时的操作，注意要把逻辑取反!和我们的按位取反~区分开来，这两个操作符也是天差地别，按位取反运算规则如下：

<code>~ 0 = 1

~ 1 = 0

按位取反是里面唯一一个单目操作符，只需要一个操作数，同时它也是最简单的，只需要将0和1对调，如下图代码：

首先我们计算对-3按位取反的结果：

<code> 11111111 11111111 11111111 11111101

按位取反：00000000 00000000 00000000 00000010

取反后是一个正数，补码就是原码，直接计算可得-3按位取反的结果为2，然后我们对5进行按位取反操作：

00000000 00000000 00000000 00000101

按位取反：11111111 11111111 11111111 11111010

可以看到取反后是一个负数，所以我们需要对它取反+1得到原码，如下：

补码：11111111 11111111 11111111 11111010

取反：10000000 00000000 00000000 00000101

加一：10000000 00000000 00000000 00000110

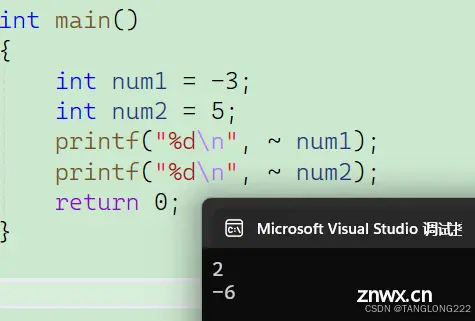
最后5按位取反的结果为-6，最后我们来看看代码执行的结果：

六、单目操作符

到目前为止我们基本上已经将单目操作符讲完了，单⽬操作符的特点是只有⼀个操作数，在单⽬操作符中只有取地址操作符和解引用操作符没有介绍，这2个操作符，我们放在学习指针的时候学习，现在来总结一下有哪些即可：

<code>//单目操作符：

！、++、--、&、*、+、-、~ 、sizeof、(类型)