【C语言】二叉树链式结构的实现,详解
池央 2024-08-21 15:35:01 阅读 54
0.前言
二叉树的基本操作的实现基本离不开一个思想——分治算法。
分治算法的基本思想是将一个规模为n的问题分解为k个规模较小的子问题,这些子问题相互独立且与原问题相同。递归地解这些子问题,然后将各子问题的解合并得到原问题的解。这样,通过逐步缩小问题的规模,可以显著降低解决问题的复杂度。
1.一颗二叉树的创建
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。先此处手动快速创建一棵简单的二树,快速进入二叉树操作学习,后面会详细说明二叉树真正的创建方式
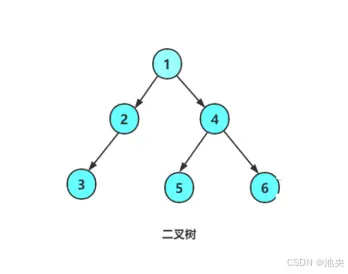
一颗二叉树分为根、左子树、右子树,该二叉树根1的左边链接根2,根2的左边链接根3,根1的右边链接根4,根4的左边链接根5,根4的右边链接根6。
<code>typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail");
return NULL;
}
newnode->left = newnode->right = NULL;
newnode->data = x;
return newnode;
}
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
2.二叉树的三种遍历方式
掌握二叉树的三种遍历方式非常重要,详细思路可看文章:二叉树的三种遍历,这里只展示代码。
2.1前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
printf("%d ", root->data);
BinaryTreePrevOrder(root->left);
BinaryTreePrevOrder(root->right);
}
2.2中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreeInOrder(root->left);
printf("%d ", root->data);
BinaryTreeInOrder(root->right);
}
2.3后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreePostOrder(root->left);
BinaryTreePostOrder(root->right);
printf("%d ", root->data);
}
3.二叉树的销毁
基本思路:和后序遍历类似,先销毁根节点的左节点,再销毁根节点的右节点,再销毁根节点。
如果按前序遍历的方式销毁,先释放掉根节点,那就找不到他的左节点和右节点。当然也可以先把要是否掉的根节点存起来,但是相较于后序遍历销毁麻烦。
3.1传一级指针
此处有个缺陷,在函数里面将根节点释放掉后置为空,并不能将实参变为空。也就是形参的改变影响不了实参。我们还需在函数外面将实参置为空。
void BinaryTreePDestory(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreePDestory(root->left);
BinaryTreePDestory(root->right);
free(root);
}
3.2传二级指针
此处形参的改变将会影响实参,不需要额外再将实参置空
void BinaryTreePPDestory(BTNode** root)
{
if (*root==NULL)
{
return;
}
BinaryTreePPDestory(&((*root)->left));
BinaryTreePPDestory(&((*root)->right));
free(*root);
*root = NULL;
}
4.二叉树节点个数
求二叉树节点个数,通常可以通过递归的方式来实现。递归的基本思想是:对于给定的二叉树,其节点总数等于左子树的节点数加上右子树的节点数,再加上根节点本身(1)。根节点为空是返回0.
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
return 0;
return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
5.二叉树叶子节点个数
叶子节点是没有左节点并且没有右节点的节点。
思路:如果当前节点为空返回0,当前节点存在且无左节点和右节点则是叶子节点返回1。如果当前节点不是叶子节点(即它有左子节点或右子节点),则递归地计算其左子树的叶子节点个数和右子树的叶子节点个数。将左子树的叶子节点个数和右子树的叶子节点个数相加,得到的结果即为以当前节点为根的子树的叶子节点总数。
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
6.二叉树第k层节点个数
思路:知道k-1层节点的左右节点一共有多少个就是二叉树第k层节点个数。当前节点为空返回0,当k等于1时说明到达第k层返回1。不等于空,且k > 1说明第k层的节点在子树里面,转换成子问题求解
int BinaryTreeLevelKSize(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->left, k - 1)
+ BinaryTreeLevelKSize(root->right, k - 1);
}
7. 二叉树查找值为x的节点
7.1只是判断该值是否在二叉中
当前节点为空返回false,当前节点的值等于x返回true,没有找到则递归到左子树里面找,没找到再去右子树找
bool TreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return false;
if (root->data == x)
return true;
return TreeFind(root->left, x) || TreeFind(root->right, x);
}
7.2返回第一个是该值的节点
当前节点为空返回,当前节点的值等于x返回该节点,没有找到则递归到左子树里面找,没找到再去右子树找(这里需要注意的是要先把节点存起来,如果没有存起来则返回的时候不会保留)
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return;
if (root->data == x)
return root;
BTNode* _left = BinaryTreeFind(root->left, x);
if (_left)
return _left;
BTNode* _right = BinaryTreeFind(root->right, x);
if (_right)
return _right;
}
8.层序遍历
层序遍历:设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。

思路:需要借助队列来实现(C语言需要自己实现队列)
首先,检查根节点是否为空,如果不为空,则将其加入队列。然后,进入一个循环,只要队列不为空,就执行以下操作:
从队列中取出一个节点(队首元素),并访问它(打印它的值),再将队列中队头的元素(也就是该节点Pop掉)
如果该节点有左子节点,则将左子节点加入队列。
如果该节点有右子节点,则将右子节点加入队列。
这个过程会按照从上到下、从左到右的顺序遍历二叉树的所有节点。
<code>void BinaryTreeLevelOrder(BTNode* root)
{
Queue pq;
QueueInit(&pq);
if (root)
{
QueuePush(&pq, root);
}
while (!QueueEmpty(&pq))
{
BTNode* front = QueueFront(&pq);
printf("%d ", front->data);
QueuePop(&pq);
if (front->left)
{
QueuePush(&pq, front->left);
}
if (front->right)
{
QueuePush(&pq, front->right);
}
}
printf("\n");
QueueDestroy(&pq);
}
9.判断二叉树是否是完全二叉树
完全二叉树:非空 空。
非完全二叉树:非空 空 非空 空
算法的思路通过层次遍历(广度优先搜索)来判断二叉树是否是完全二叉树。
首先,我们初始化一个队列,并将根节点(如果存在)加入队列中。然后,我们进入一个循环,不断地从队列中取出节点,并尝试将其左右子节点加入队列。如果在某个时刻,我们遇到了一个空节点(即该节点不存在)跳出第一个循环另外判断,不再向队列中添加任何子节点。这是因为,在完全二叉树的定义中,一旦开始遇到空节点,其后的所有节点都应该是空的。
在遍历完所有可能存在的节点后(即所有非空节点的子节点都已经被考虑过),我们再次检查队列。如果此时队列为空,说明我们之前的假设成立,即该二叉树是完全二叉树。如果队列不为空,且队列中的节点不为空,那么说明在之前遇到空节点之后,还有非空节点存在,这与完全二叉树的定义相违背,因此该二叉树不是完全二叉树。
简而言之,这个算法通过层次遍历来检查二叉树是否满足完全二叉树的性质:除了最后一层外,每一层都被完全填满,并且所有节点都尽可能地向左对齐。
bool BinaryTreeComplete(BTNode* root)
{
Queue pq;
QueueInit(&pq);
if (root)
{
QueuePush(&pq, root);
}
while (!QueueEmpty(&pq))
{
BTNode* front = QueueFront(&pq);
QueuePop(&pq);
//遇到空以后跳出后续判断
if (front == NULL)
{
break;
}
QueuePush(&pq, front->left);
QueuePush(&pq, front->right);
}
//是空出队列,遇见非空则说明不是完全二叉树
while (!QueueEmpty(&pq))
{
BTNode* front = QueueFront(&pq);
QueuePop(&pq);
if (front)
{
QueueDestroy(&pq);
return false;
}
}
QueueDestroy(&pq);
return true;
}
10.二叉树的创建
我们可以借助这道题目来理解:二叉树的遍历

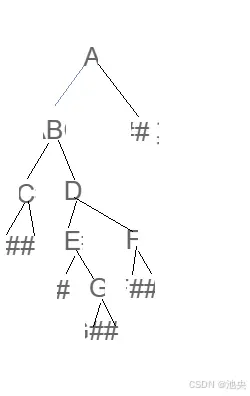
二叉树的形状
按前序遍历的方式创建一颗二叉树,三个参数数组,数组长度,数组下标(初始值设为0)
当*pi>=数组越界或者数组元素等于#时数组下标+1且返回空,
把数组元素赋给节点数据,
递归,让数组的数据按照前序遍历的方式依次赋给节点。
<code>BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
if (*pi >= n || a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
root->data = a[*pi];
(*pi)++;
root->left = BinaryTreeCreate(a, n, pi);
root->right = BinaryTreeCreate(a, n, pi);
return root;
}
11.完整代码(包括队列的实现)
11.1BinaryTree.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
#include"Queue.h"
BTNode* BuyNode(BTDataType x);
//二叉树的创建
BTNode* CreatBinaryTree();
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreePDestory(BTNode* root);
void BinaryTreePPDestory(BTNode** root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
bool TreeFind(BTNode* root, BTDataType x);
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);
11.2Queue.h
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdbool.h>
#include<stdlib.h>
#include"BinaryTree.h"
typedef struct BinaryTreeNode* QDataType;
typedef struct QueueNode
{
QDataType val;
struct QueueNode* next;
}QNode;
typedef struct Queue
{
QNode* phead;
QNode* ptail;
int size;
}Queue;
//初始化
void QueueInit(Queue* pq);
//销毁
void QueueDestroy(Queue* pq);
//判空
bool QueueEmpty(Queue* pq);
//入队列
void QueuePush(Queue* pq, QDataType x);
//出队列
void QueuePop(Queue* pq);
//取队头
QDataType QueueFront(Queue* pq);
//取队尾
QDataType QueueBack(Queue* pq);
//队列长度
size_t QueueLength(Queue* pq);
11.3Queue.c
#include"Queue.h"
//初始化
void QueueInit(Queue* pq)
{
assert(pq);
pq->phead = pq->ptail = NULL;
pq->size = 0;
}
//销毁
void QueueDestroy(Queue* pq)
{
assert(pq);
QNode* cur = pq->phead;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->phead = pq->ptail = NULL;
pq->size = 0;
}
//入队列
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
//在队尾入,尾插
//创建新节点
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc fail");
return;
}
newnode->val = x;
newnode->next = NULL;
//空链表
if (QueueEmpty(pq))
{
pq->phead = pq->ptail = newnode;
}
else
{
pq->ptail->next = newnode;
pq->ptail = newnode;
}
pq->size++;
}
//出队列
void QueuePop(Queue* pq)
{
assert(pq);
//零个节点
assert(pq->phead);
//一个节点
if (pq->phead->next == NULL)
{
free(pq->phead);
pq->phead = pq->ptail = NULL;
}
else
{
QNode* next = pq->phead->next;
free(pq->phead);
pq->phead = next;
}
pq->size--;
}
//判空
bool QueueEmpty(Queue* pq)
{
assert(pq);
return pq->size == 0;
}
//取队头
QDataType QueueFront(Queue* pq)
{
assert(pq);
assert(pq->phead);
return pq->phead->val;
}
//取队尾
QDataType QueueBack(Queue* pq)
{
assert(pq);
assert(pq->ptail);
return pq->ptail->val;
}
//队列长度
size_t QueueLength(Queue* pq)
{
assert(pq);
return pq->size;
}
11.4BinaryTree.c
#include"BinaryTree.h"
BTNode* BuyNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail");
return NULL;
}
newnode->left = newnode->right = NULL;
newnode->data = x;
return newnode;
}
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
if (*pi >= n || a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
root->data = a[*pi];
(*pi)++;
root->left = BinaryTreeCreate(a, n, pi);
root->right = BinaryTreeCreate(a, n, pi);
return root;
}
// 二叉树销毁
//传一级指针
void BinaryTreePDestory(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreePDestory(root->left);
BinaryTreePDestory(root->right);
free(root);
}
//传二级指针
void BinaryTreePPDestory(BTNode** root)
{
if (*root==NULL)
{
return;
}
BinaryTreePPDestory(&((*root)->left));
BinaryTreePPDestory(&((*root)->right));
free(*root);
*root = NULL;
}
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
return 0;
return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
// 二叉树查找值为x的节点
bool TreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return false;
if (root->data == x)
return true;
return TreeFind(root->left, x) || TreeFind(root->right, x);
}
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return;
if (root->data == x)
return root;
BTNode* _left = BinaryTreeFind(root->left, x);
if (_left)
{
return _left;
}
BTNode* _right = BinaryTreeFind(root->right, x);
if (_right)
{
return _right;
}
}
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
printf("%d ", root->data);
BinaryTreePrevOrder(root->left);
BinaryTreePrevOrder(root->right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreeInOrder(root->left);
printf("%d ", root->data);
BinaryTreeInOrder(root->right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreePostOrder(root->left);
BinaryTreePostOrder(root->right);
printf("%d ", root->data);
}
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
Queue pq;
QueueInit(&pq);
if (root)
{
QueuePush(&pq, root);
}
while (!QueueEmpty(&pq))
{
BTNode* front = QueueFront(&pq);
printf("%d ", front->data);
QueuePop(&pq);
if (front->left)
{
QueuePush(&pq, front->left);
}
if (front->right)
{
QueuePush(&pq, front->right);
}
}
printf("\n");
QueueDestroy(&pq);
}
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
Queue pq;
QueueInit(&pq);
if (root)
{
QueuePush(&pq, root);
}
while (!QueueEmpty(&pq))
{
BTNode* front = QueueFront(&pq);
QueuePop(&pq);
//遇到空以后跳出后续判断
if (front == NULL)
{
break;
}
QueuePush(&pq, front->left);
QueuePush(&pq, front->right);
}
//是空出队列,遇见非空则说明不是完全二叉树
while (!QueueEmpty(&pq))
{
BTNode* front = QueueFront(&pq);
QueuePop(&pq);
if (front)
{
QueueDestroy(&pq);
return false;
}
}
QueueDestroy(&pq);
return true;
}
11.5test.c
#include"BinaryTree.h"
int main()
{
BTNode* root = CreatBinaryTree();
// 前序遍历
BinaryTreePrevOrder(root);
printf("\n");
// 中序遍历
BinaryTreeInOrder(root);
printf("\n");
// 后序遍历
BinaryTreePostOrder(root);
printf("\n");
// 判断二叉树是否是完全二叉树
bool flag = BinaryTreeComplete(root);
printf("%d\n", flag);
//层序遍历
BinaryTreeLevelOrder(root);
//二叉树查找值为x的节点
bool flag1 = TreeFind(root, 3);
BTNode* root1 = BinaryTreeFind(root, 3);
// 二叉树第k层节点个数
int KSize = BinaryTreeLevelKSize(root, 3);
printf("%d\n", KSize);
// 二叉树叶子节点个数
int leaf = BinaryTreeLeafSize(root);
printf("%d\n", leaf);
//二叉树节点个数
int size = BinaryTreeSize(root);
printf("%d\n", size);
// 销毁
BinaryTreePPDestory(&root);
root = NULL;
}

欢迎各位大佬一起学习交流
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。