个人主页：NiKo

算法专栏：算法设计与分析

目录

题目 2680:纸张尺寸 

题目 2664:求和

题目 2681: 矩形拼接

题目 2665: 选数异或

题目 2682: GCD

题目 2667: 青蛙过河

题目 2683: 因数平方和

题目 2668: 最长不下降子序列

题目 2680:纸张尺寸 

题目描述

        在 ISO 国际标准中定义了 A0 纸张的大小为 1189mm × 841mm，将 A0 纸沿长边对折后为 A1 纸，大小为 841mm × 594mm，在对折的过程中长度直接取下整（实际裁剪时可能有损耗）。将 A1 纸沿长边对折后为 A2 纸，依此类推。 输入纸张的名称，请输出纸张的大小。

输入格式

        输入一行包含一个字符串表示纸张的名称，该名称一定是 A0、A1、A2、A3、A4、A5、A6、A7、A8、A9 之一。 

输出格式

        输出两行，每行包含一个整数，依次表示长边和短边的长度。

样例输入

<code>A0

样例输出

1189

841

题解

#include<stdio.h>

int main()

{

char let;

int num;

int long_ = 1189,short_ = 841;

int newlong = long_,newshort = short_;

scanf("%c%d",&let,&num);

int type = num;

if(type==0){

printf("%d\n",1189);

printf("%d",841);

}else{

while(type){

// 长边对折

newlong = long_ / 2;

if(newlong < short_){

int temp = short_;

short_ = newlong;

long_ = temp;

}

type--;

}

printf("%d\n",long_);

printf("%d",short_);

}

return 0;

}

题目 2664:求和

题目描述

        给定 n 个整数 a1, a2, · · · , an ，求它们两两相乘再相加的和，即 S = a1 · a2 + a1 · a3 + · · · + a1 · an + a2 · a3 + · · · + an-2 · an-1 + an-2 · an + an-1 · an.

输入格式

输入的第一行包含一个整数 n 。 

第二行包含 n 个整数 a1, a2, · · · an。

输出格式

输出一个整数 S，表示所求的和。请使用合适的数据类型进行运算。

样例输入

4

1 3 6 9

样例输出

117

提示

对于 30% 的数据，1 ≤ n ≤ 1000，1 ≤ ai ≤ 100。

对于所有评测用例，1 ≤ n ≤ 200000，1 ≤ ai ≤ 1000。

题解

#include<bits/stdc++.h>

using namespace std;

int main(void){

ios_base::sync_with_stdio(0);cin.tie(0);

int n;

cin>>n;

long long sum[200001];

long long ans=0;

int a;

cin>>a;

sum[1]=a;

for(int i=2;i<=n;++i){

cin>>a;

sum[i]=sum[i-1]+a;

ans+=a*sum[i-1];

}

cout<<ans;

return 0;

}

题目 2681: 矩形拼接

题目描述

已知 3 个矩形的大小依次是 a1 × b1, a2 × b2 和 a3 × b3。用这 3 个矩形能拼出的所有多边形中，边数最少可以是多少？例如用 3 × 2 的矩形（用 A 表示）、4 × 1 的矩形（用 B 表示）和 2 × 4 的矩形（用 C 表示）可以拼出如下 4 边形。

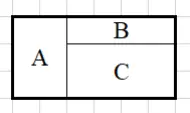
例如用 3 × 2 的矩形（用 A 表示）、3 × 1 的矩形（用 B 表示）和 1 × 1 的矩形（用 C 表示）可以拼出如下 6 边形。

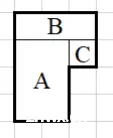
输入格式

输入包含多组数据。

第一行包含一个整数 T，代表数据组数。

以下 T 行，每行包含 6 个整数 a1, b1, a2, b2, a3, b3，其中 a1, b1 是第一个矩形的边长，a2, b2 是第二个矩形的边长，a3, b3 是第三个矩形的边长。

输出格式

对于每组数据，输出一个整数代表答案。

样例输入

<code>2

2 3 4 1 2 4

1 2 3 4 5 6

样例输出

4

6

提示

对于 10% 的评测用例，1 ≤ T ≤ 5，1 ≤ a1, b1, a2, b2, a3, b3 ≤ 10，a1 = a2 = a3。

对于 30% 的评测用例，1 ≤ T ≤ 5，1 ≤ a1, b1, a2, b2, a3, b3 ≤ 10。

对于 60% 的评测用例，1 ≤ T ≤ 10，1 ≤ a1, b1, a2, b2, a3, b3 ≤ 20。

对于所有评测用例，1 ≤ T ≤ 1000，1 ≤ a1, b1, a2, b2, a3, b3 ≤ 100。

题解

#include<bits/stdc++.h>

using namespace std;

int a[3][2];

int main()

{

int T;

cin >> T;

while (T--)

{

//输入三个矩形的长和宽

for (int i = 0; i < 3; i++)

cin >> a[i][0] >> a[i][1];

int ans = 8;//完全不匹配时的答案为8

for (int i = 0; i < 3; i++)//枚举第一个矩形

for (int j = 0; j < 3; j++)

if (i != j)//枚举第二个矩形

for (int k = 0; k < 3; k++)

if (i != k && j != k)//枚举第三个矩形

for (int ii = 0; ii <= 1; ii++)//枚举第一个矩形的长宽

for (int jj = 0; jj <= 1; jj++)//枚举第二个矩形的长宽

for (int kk = 0; kk <= 1; kk++)//枚举第三个矩形的长宽

{

//第一个矩形的长等于后两个矩形的长之和

if (a[i][ii] == a[j][jj] + a[k][kk])

{

ans = min(ans, 6);

//后面两个矩形的宽相等

if (a[j][1 - jj] == a[k][1 - kk])

ans = min(ans, 4);

}

//至少有一个矩形的长和第一个矩形的长相等

if (a[i][ii] == a[j][jj] || a[i][ii] == a[k][kk])

ans = min(ans, 6);

//三个矩形的长全部相等

if (a[i][ii] == a[j][jj] && a[i][ii] == a[k][kk])

ans = min(ans, 4);

}

cout << ans << endl;

}

return 0;

}

题目 2665: 选数异或

题目描述

给定一个长度为 n 的数列 A1, A2, · · · , An 和一个非负整数 x，给定 m 次查询, 每次询问能否从某个区间 [l,r] 中选择两个数使得他们的异或等于 x 。

输入格式

输入的第一行包含三个整数 n, m, x 。

第二行包含 n 个整数 A1, A2, · · · , An 。

接下来 m 行，每行包含两个整数 li ,ri 表示询问区间 [li ,ri ] 。

输出格式

对于每个询问, 如果该区间内存在两个数的异或为 x 则输出 yes, 否则输出 no。

样例输入

4 4 1

1 2 3 4

1 4

1 2

2 3

3 3

样例输出

yes

no

yes

no

提示

显然整个数列中只有 2, 3 的异或为 1。

对于 20% 的评测用例，1 ≤ n, m ≤ 100；

对于 40% 的评测用例，1 ≤ n, m ≤ 1000；

对于所有评测用例，1 ≤ n, m ≤ 100000 ，0 ≤ x < 2的20次方 ，1 ≤ li ≤ ri ≤ n ， 0 ≤ Ai < 2的20次方。 

题解

#include<bits/stdc++.h>

using namespace std;

int main(void){

ios_base::sync_with_stdio(0);cin.tie(0);

int n,m,x;

cin>>n>>m>>x;

int arry[100002];

unordered_map<int,vector<int>> Map; //记录值和所有下标

vector<vector<int>> ans;

for(int i=1;i<=n;++i){//O(n)

cin>>arry[i];

if(Map.find(arry[i])==Map.end())

Map[arry[i]]={i};

else Map[arry[i]].emplace_back(i);

}

for(int i=1;i<=n;++i){//O(n*pair)

if(Map.find(arry[i]^x)!=Map.end()){

//i 与 Map[arry[i]^x] 这俩位置可以异或为x

int temp=arry[i]^x;

for(int j=0;j<Map[temp].size();++j){

//由于答案是成对出现的，这里肯定会出现重复，但是不一定对称

ans.push_back({min(i,Map[temp][j]),max(i,Map[temp][j])});

}

}

}

while(m--){

int left,right;

cin>>left>>right;

bool flag=true;

for(int j=0;j<ans.size();++j){//O(m*pair)

if(left<=ans[j][0]&&right>=ans[j][1]){

cout<<"yes"<<'\n';

flag=false;

break;

}

}

if(flag)

cout<<"no"<<'\n';

}

return 0;

}

题目 2682: GCD

题目描述

给定两个不同的正整数 a, b，求一个正整数 k 使得 gcd(a + k, b + k) 尽可能大，其中 gcd(a, b) 表示 a 和 b 的最大公约数，如果存在多个 k，请输出所有满足条件的 k 中最小的那个。 

输入格式

输入一行包含两个正整数 a, b，用一个空格分隔。 

输出格式

输出一行包含一个正整数 k。

样例输入

5 7

样例输出

1

提示

对于 20% 的评测用例，a < b ≤ 10的5次方 ；

对于 40% 的评测用例，a < b ≤ 10的9次方 ；

对于所有评测用例，1 ≤ a < b ≤ 10的18次方 。

题解

#include<iostream>

using namespace std;

int main()

{

long long a,b,c,d;

cin>>a>>b;

if(a>b){

long long t=a;

a=b;

b=t;

}

c=b-a;

d=a/c;

if(a%c)

d++;

cout<<d*c-a<<endl;

return 0;

}

题目 2667: 青蛙过河

题目描述

小青蛙住在一条河边，它想到河对岸的学校去学习。小青蛙打算经过河里的石头跳到对岸。

河里的石头排成了一条直线，小青蛙每次跳跃必须落在一块石头或者岸上。不过，每块石头有一个高度，每次小青蛙从一块石头起跳，这块石头的高度就会下降 1，当石头的高度下降到 0 时小青蛙不能再跳到这块石头上（某次跳跃后使石头高度下降到 0 是允许的）。

小青蛙一共需要去学校上 x 天课，所以它需要往返 2x 次。当小青蛙具有一个跳跃能力 y 时，它能跳不超过 y 的距离。

请问小青蛙的跳跃能力至少是多少才能用这些石头上完 x 次课。

输入格式

输入的第一行包含两个整数 n, x，分别表示河的宽度和小青蛙需要去学校的天数。请注意 2x 才是实际过河的次数。

第二行包含 n − 1 个非负整数 H1, H2, · · · , Hn-1，其中 Hi > 0 表示在河中与小青蛙的家相距 i 的地方有一块高度为 Hi 的石头，Hi = 0 表示这个位置没有石头。

输出格式

输出一行，包含一个整数，表示小青蛙需要的最低跳跃能力。

样例输入

5 1

1 0 1 0

样例输出

4

提示

由于只有两块高度为 1 的石头，所以往返只能各用一块。第 1 块石头和对岸的距离为 4，如果小青蛙的跳跃能力为 3 则无法满足要求。所以小青蛙最少需要 4 的跳跃能力。 

对于 30% 的评测用例，n ≤ 100；

对于 60% 的评测用例，n ≤ 1000；

对于所有评测用例，1 ≤ n ≤ 10的5次方 , 1 ≤ x ≤ 10的9次方 , 1 ≤ Hi ≤ 10的4次方。

题解

#include <iostream>

#include <cstring>

#include <algorithm>

#include <stack>

using namespace std;

typedef long long LL;

typedef pair<int,int>pii;

const int mod = 1e9 + 7 , INF = 0x3f3f3f3f , N = 1e5 + 10;

int n,m;

int a[N];

bool check(int x)

{

// 如果所有长度为x的区间都大于等于m ，则true

int s = 0;

for (int i = 1 ; i <= min(n - 1,x) ; i ++)

s += a[i];

if (s < m)

return false;

for (int i = x + 1; i <= n - 1; i ++)

{

s -= a[i - x];

s += a[i];

if (s < m)

return false;

}

return s >= m;

}

int main()

{

cin >> n >> m;

m *= 2;

for (int i = 1 ; i <= n - 1 ; i ++)

cin >> a[i];

int l = 0,r = n;

while (l < r)

{

int mid = l + r >> 1;

if (check(mid))

r = mid;

else

l = mid + 1;

}

cout << r << endl;

}

题目 2683: 因数平方和

题目

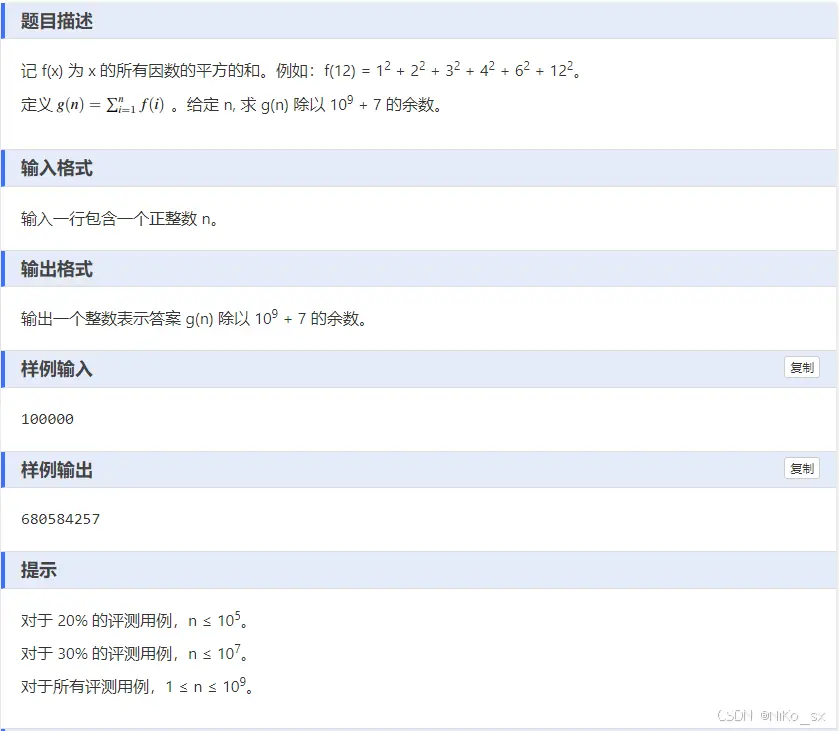
 题解

<code>import java.time.format.DateTimeFormatter;

import java.time.LocalDateTime;

public class Test {

public static void main(String[] args) { new Test().run(); }

void run() {

DateTimeFormatter date = DateTimeFormatter.ofPattern("MMdd");

DateTimeFormatter time = DateTimeFormatter.ofPattern("HHmm");

LocalDateTime start = LocalDateTime.of(0000, 01, 01, 00, 00);

LocalDateTime end = LocalDateTime.of(0000, 12, 31, 23, 59);

int[] buff = new int[128];

int ans = 0;

for (; start.compareTo(end) <= 0; start = start.plusMinutes(1)) {

for (char i = '0'; i <= '9'; ++i) buff[i] = 0;

for (byte b : start.format(date).getBytes()) ++buff[b];

boolean flag1 = true, flag3 = true;

for (char i = '0'; i <= '9'; ++i)

if (buff[i] == 1) flag1 = false;

else if (buff[i] == 3) flag3 = false;

if (flag1 || flag3) continue;

for (byte b : start.format(time).getBytes()) --buff[b];

for (char i = '0'; i <= '9'; ++i)

if (buff[i] != 0) flag1 = true;

if (!flag1) ++ans;

}

System.out.println(4 * ans);

}

}

题目 2668: 最长不下降子序列

题目

 题解

<code>package leetcode板块;

import java.util.Arrays;

import java.util.Scanner;

public class _题目2668蓝桥杯2022年第十三届省赛真题_最长不下降子序列 {

/**

*

* @param args

*/

public static void main(String[] args) {

// 现在你有一次机会，将其中【连续的 K 个数】 修改成 【任意一个相同值】。

// 请你计算如何修改可以使修改后的数列的最长不下降子序列最长，请输出这个最长的长度。

// TODO 最长不下降子序列是指序列中的一个子序列，子序列中的每个数不小于在它之前的数。

/*

对于所有评测用例，1 ≤ K ≤ N ≤ 10^5，1 ≤ Ai ≤ 10^6。

*/

Scanner scanner = new Scanner(System.in);

// 长度为 N , 将其中连续的 K 个数修改成任意一个相同值

int N = scanner.nextInt();

int K = scanner.nextInt();

int arrA [] = new int[N];

for (int i = 0; i<N;i++){

arrA[i] = scanner.nextInt();

}

scanner.close();

// 重点 ： LNDS:longest non-decreasing subsequence

int initLNDS = computeLNDS(arrA);

int maxLNDS = initLNDS;

// ----------------------------------------------

for (int i = 0; i <= N-K;i++){

int [] original = Arrays.copyOfRange(arrA,i,i+K);

int uniqueVals [] = Arrays.stream(arrA).distinct().toArray();

for (int value : uniqueVals){

for (int j = i;j<i+K;j++){

arrA[j] = value;

}

int modifiedLNDS = computeLNDS(arrA);

maxLNDS = Math.max(maxLNDS,modifiedLNDS);

}

System.arraycopy(original,0,arrA,i,K);

}

System.out.println(maxLNDS);

}

/**

*

* @param array

* @return

*/

private static int computeLNDS(int[] array) {

int [] dp_computeLNDS = new int[array.length];

int length = 0;

for (int num : array){

int pos = Arrays.binarySearch(dp_computeLNDS,0,length,num);

if (pos < 0){

pos = -(pos + 1);

}

dp_computeLNDS[pos] = num;

if (pos == length){

length++;

}

}

return length;

}

}