1.定义

RANSAC（Random Sample Consensus）算法是一种基于随机采样的迭代算法，用于估计一个数学模型参数。它最初由Fischler和Bolles于1981年提出，主要用于计算机视觉和计算机图形学中的模型拟合和参数估计问题。

RANSAC算法的基本思想是通过随机采样一小部分数据来估计模型参数，然后用这个模型对所有数据进行测试，将满足模型的数据点作为内点，不满足模型的数据点作为外点。通过迭代的方式不断随机采样和估计模型参数，最终得到内点数目最多的模型作为最终的估计结果。

RANSAC算法的优点是可以处理包含大量外点的数据集，并且不需要事先知道外点的数量。它可以用于解决许多计算机视觉和计算机图形学中的问题，如图像配准、物体识别、三维重建、特征点匹配等。

应用：

1.在点云中我们要平面

2.求解基础矩阵和本质矩阵

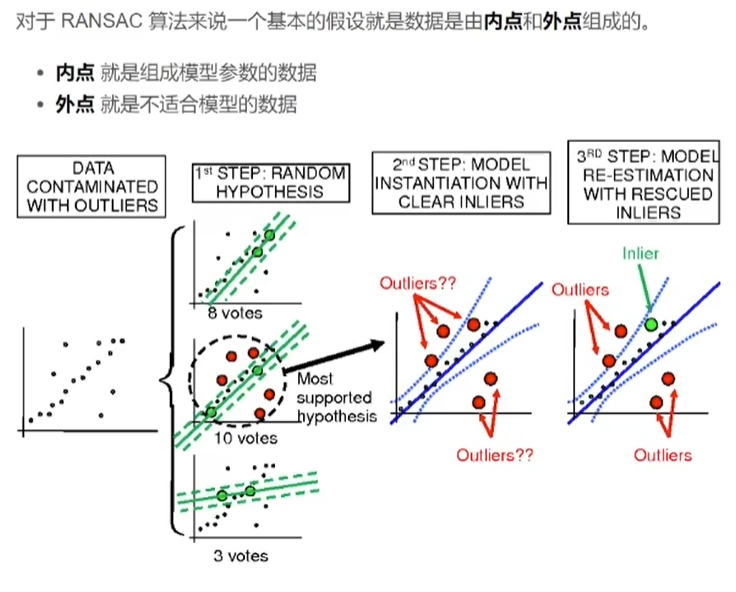
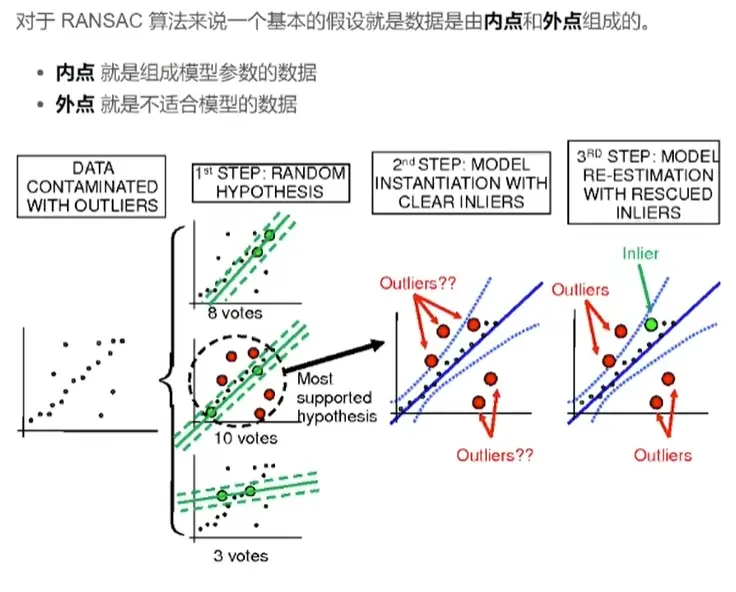
2.基本步骤

需要注意的是，RANSAC算法的可靠性取决于内点比例和迭代次数，内点比例越高，越容易得到正确的估计结果。但是，随着内点比例的增加，需要的迭代次数也会增加。因此，算法的可靠性和效率需要平衡考虑。

总之，RANSAC算法的基本步骤是随机采样、模型估计、内点外点分类、重复迭代以及最终模型选择。通过迭代的方式逐步提高模型的可靠性，最终得到准确的模型参数。

3.外点率和自适应RANSAC

也就是说，每一次迭代，建立一个模型，得到外点率，计算相应的N1,记录count；再次迭代建立模型，得到新的外点率和N，应比上一次要小，这样一来N更新，同时更新count

4.如何计算迭代次数

5.RANSAC算法在C++中的实现：

1）PCL（点云库）

PCL是一个功能强大的点云处理库，其中包含了许多用于3D点云处理的算法，包括RANSAC。它提供了一组现成的数据结构和算法，可用于点云滤波、分割、重建等应用中。

2）OpenCV

OpenCV是一个开源的计算机视觉库，也可以用于3D点云处理。它提供了许多用于3D点云处理的函数和类，包括RANSAC和其它一些用于计算几何的工具。

3）CGAL

CGAL是一个计算几何算法库，也包含了一些用于3D点云处理的算法和数据结构。其中包括用于拟合平面和直线的RANSAC算法。

这些库都可以在C++中用于实现RANSAC-3D算法。选择哪一个库取决于你的具体需求和应用场景。如果你主要需要处理点云数据，那么PCL可能是一个不错的选择。如果你需要进行更一般的计算几何任务，那么CGAL可能更适合你。如果你已经熟悉OpenCV，那么它也可以作为一个选择。

6.Python中相关示例代码

pyransac-3d库官网：pyRANSAC-3D

​import numpy as npfrom sklearn.neighbors import NearestNeighborsfrom sklearn.decomposition import PCAdef ransac_3d(data, n, k, t, d): """ RANSAC-3D algorithm for plane fitting :param data: 3D point cloud data :param n: the minimum number of points to fit a plane :param k: the maximum number of iterations :param t: the inlier distance threshold :param d: the number of inliers required to accept the result :return: the best fit plane model and the corresponding inliers """ best_model = None best_inliers = None for i in range(k): # Randomly select n points indices = np.random.choice(data.shape[0], n, replace=False) sample = data[indices, :] # Fit a plane to the sample points pca = PCA(n_components=3) pca.fit(sample) normal = pca.components_[2, :] point = np.mean(sample, axis=0) plane = np.append(normal, -np.dot(normal, point)) # Compute the distance between each point and the plane distances = np.abs(np.dot(data, plane[:-1]) + plane[-1]) inliers = np.where(distances < t)[0] # Check if we have enough inliers to accept the result if len(inliers) >= d: # Refit the plane to all inliers sample = data[inliers, :] pca = PCA(n_components=3) pca.fit(sample) normal = pca.components_[2, :] point = np.mean(sample, axis=0) plane = np.append(normal, -np.dot(normal, point)) # Save the model if it is better than the current best if best_inliers is None or len(inliers) > len(best_inliers): best_model = plane best_inliers = inliers return best_model, best_inliers​

这个算法使用NumPy、Scikit-learn和PCA库来实现，其中Scikit-learn库中的NearestNeighbors类可用于查找最近邻点，PCA类可用于拟合平面。函数中的参数n、k、t和d分别是算法中的最小样本数、迭代次数、阈值和最小内点数。

7.变体：

1）随机RANSAC算法：

随机抽样一致性算法（Random Sample Consensus，RANSAC）是一种迭代算法，用于估计数学模型的参数。它在计算机视觉和计算机图形学等领域中得到了广泛应用，例如拟合线、平面、圆等几何形状、匹配图像特征等。

在随机 RANSAC 模型中，我们首先从数据集中随机选择一组点来构建初始模型。然后，我们对数据集中的每个数据点进行测试，看它是否与当前模型匹配。如果一个数据点与模型匹配，我们称其为内点。否则，我们称其为外点。

在每一次迭代中，我们都会随机选择一些数据点来构建新的模型，并测试数据集中的每个点是否与新模型匹配。我们计算模型能够匹配的内点数量，将此数量称为内点数。我们记录内点数最大的模型，并将内点数大于预设阈值的点作为新的内点集合。

如果我们达到了预设的迭代次数或者已经找到了足够好的模型，则停止迭代，并返回内点最多的模型。如果我们没有找到足够好的模型，则需要重新进行随机抽样，重复上述过程。

需要注意的是，在随机 RANSAC 中，初始模型的选择是随机的，每次迭代中构建新模型的点集也是随机选择的。这种随机性使得算法具有一定的随机性，因此可以在一定程度上避免局部最优解的出现。

随机 RANSAC 模型和 RANSAC 模型都是用于估计数学模型参数的迭代算法，它们的基本思想是一致的，但是它们在实现细节上存在一些差异。

相同点：

都是迭代算法，用于估计数学模型的参数。都是基于数据点的内点和外点的概念。都采用了随机性来避免局部最优解。

不同点：

随机 RANSAC 模型在每次迭代时，随机选择一些数据点来构建新的模型，而 RANSAC 模型则是从数据集中选择一组点来构建初始模型，然后在每次迭代中选择与当前模型匹配的点来更新模型。随机 RANSAC 模型的初始模型是随机选择的，而 RANSAC 模型是通过数据集中选择一组点来构建的。随机 RANSAC 模型迭代时不断随机选择点集来构建模型，每次迭代中的模型参数不一定相同，而 RANSAC 模型在每次迭代中的模型参数是固定的。随机 RANSAC 模型在每次迭代中都会记录内点数最多的模型，而 RANSAC 模型在每次迭代中只记录内点数最大的模型。随机 RANSAC 模型可以在一定程度上避免局部最优解，但也可能因为随机性导致不同的运行结果不同，而 RANSAC 模型不会受到随机性的影响，可以保证得到相同的结果。

代码实现：

import randomimport numpy as npdef ransac(data, model, n, k, t, d, debug=False, return_all=False): """ 随机 RANSAC 算法 :param data: 数据点集，包含 x 和 y 坐标的数组 :param model: 模型函数，需要输入数据点和模型参数，返回模型估计值 :param n: 用于估计模型所需的最小数据点数 :param k: 迭代次数 :param t: 阈值，用于判断数据点是否与模型匹配 :param d: 数据点集合模型匹配的内点数阈值 :param debug: 是否输出调试信息 :param return_all: 是否返回所有模型参数 :return: 返回估计的模型参数 """ iterations = 0 best_model = None best_inliers = [] best_error = np.inf while iterations < k: # 随机选择 n 个数据点，估计模型参数 maybe_inliers = random.sample(data, n) maybe_model = model(maybe_inliers) # 用模型估计值测试所有数据点，找到内点 also_inliers = [] for point in data: if point in maybe_inliers: continue if model([point], maybe_model, t): also_inliers.append(point) # 如果内点数大于 d，我们认为找到了足够好的模型 if len(also_inliers) > d: # 用所有内点重新估计模型参数 better_model = model(maybe_inliers + also_inliers) # 计算内点均方误差 this_error = model_error(better_model, maybe_inliers + also_inliers) # 如果均方误差更小，记录此模型 if this_error < best_error: best_model = better_model best_inliers = maybe_inliers + also_inliers best_error = this_error if debug: print('RANSAC Iteration {}/{}'.format(iterations + 1, k)) print(' Number of inliers: {}'.format(len(also_inliers))) print(' Best error: {}'.format(best_error)) iterations += 1 if best_model is None: raise ValueError("RANSAC failed to find a good model.") if return_all: return best_model, best_inliers else: return best_model def model_error(model, points): """ 计算模型估计值与数据点之间的均方误差 :param model: 模型函数 :param points: 数据点 :return: 均方误差 """ error = 0 for point in points: error += (model(point) - point[1]) ** 2 return error / len(points)

在这个实现中，data 是数据点的集合，model 是估计模型的函数，n 是用于估计模型所需的最小数据