HNU_AI_作业3--贝叶斯网络、不确定性的量化、决策树、人工神经网络、深度学习
_蟑螂恶霸_ 2024-06-17 14:01:02 阅读 80
参考:
HNU岳麓山大小姐-人工智能导论:清览作业
QCNH雨文-人工智能作业三
DONT_1.3概念基础——深度学习基本原理
1.贝叶斯网络
根据图所给出的贝叶斯网络,其中:P(A)=0.5,P(B|A)=1, P(B|¬A)=0.5, P(C|A)=1, P(C|¬A)=0.5,P(D|BC)=1,P(D|B, ¬C)=0.5,P(D|¬B,C)=0.5,P(D|¬B, ¬C)=0。试计算下列概率P(A|D)。
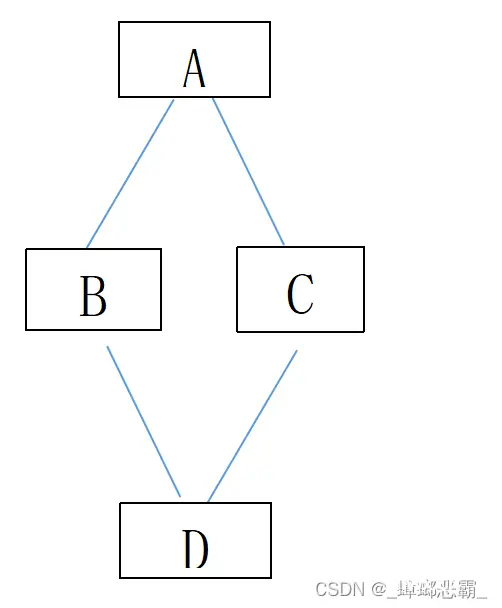
解:
P ( A ∣ D ) = P ( D ∣ A ) ∗ P ( A ) P ( D ) P(A|D) = \frac {P(D|A)*P(A)} {P(D)} P(A∣D)=P(D)P(D∣A)∗P(A)
P ( D ∣ A ) ∗ P ( A ) = P ( D ∣ B C ) ∗ P ( B ∣ A ) P ( C ∣ A ) ∗ P ( A ) + P ( D ∣ ¬ B C ) ∗ P ( ¬ B ∣ A ) P ( C ∣ A ) ∗ P ( A ) + P ( D ∣ B ¬ C ) ∗ P ( B ∣ A ) P ( ¬ C ∣ A ) ∗ P ( A ) + P ( D ∣ ¬ B ¬ C ) ∗ P ( ¬ B ∣ A ) P ( ¬ C ∣ A ) ∗ P ( A ) = 1 ∗ 1 ∗ 1 ∗ 0.5 + 0.5 ∗ 0 ∗ 1 ∗ 0.5 + 0.5 ∗ 1 ∗ 0 ∗ 0.5 + 0 ∗ 0 ∗ 0 ∗ 0.5 = 0.5 P(D|A)*P(A) = P(D|BC)*P(B|A)P(C|A)*P(A)+P(D|¬BC)*P(¬B|A)P(C|A)*P(A) \\ +P(D|B¬C)*P(B|A)P(¬C|A)*P(A)+P(D|¬B¬C)*P(¬B|A)P(¬C|A)*P(A) \\ = 1*1*1*0.5+0.5*0*1*0.5+0.5*1*0*0.5+0*0*0*0.5 \\=0.5 P(D∣A)∗P(A)=P(D∣BC)∗P(B∣A)P(C∣A)∗P(A)+P(D∣¬BC)∗P(¬B∣A)P(C∣A)∗P(A)+P(D∣B¬C)∗P(B∣A)P(¬C∣A)∗P(A)+P(D∣¬B¬C)∗P(¬B∣A)P(¬C∣A)∗P(A)=1∗1∗1∗0.5+0.5∗0∗1∗0.5+0.5∗1∗0∗0.5+0∗0∗0∗0.5=0.5
P ( D ∣ ¬ A ) ∗ P ( ¬ A ) = P ( D ∣ B C ) ∗ P ( B ∣ ¬ A ) P ( C ∣ ¬ A ) ∗ P ( ¬ A ) + P ( D ∣ ¬ B C ) ∗ P ( ¬ B ∣ ¬ A ) P ( C ∣ ¬ A ) ∗ P ( ¬ A ) + P ( D ∣ B ¬ C ) ∗ P ( B ∣ ¬ A ) P ( ¬ C ∣ ¬ A ) ∗ P ( ¬ A ) + P ( D ∣ ¬ B ¬ C ) ∗ P ( ¬ B ∣ ¬ A ) P ( ¬ C ∣ ¬ A ) ∗ P ( ¬ A ) = 1 ∗ 0.5 ∗ 0.5 ∗ 0.5 + 0.5 ∗ 0.5 ∗ 0.5 ∗ 0.5 + 0.5 ∗ 0.5 ∗ 0.5 ∗ 0.5 + 0 ∗ 0.5 ∗ 0.5 ∗ 0.5 = 0.25 P(D|¬A)*P(¬A) = P(D|BC)*P(B|¬A)P(C|¬A)*P(¬A)+P(D|¬BC)*P(¬B|¬A)P(C|¬A)*P(¬A) \\ +P(D|B¬C)*P(B|¬A)P(¬C|¬A)*P(¬A)+P(D|¬B¬C)*P(¬B|¬A)P(¬C|¬A)*P(¬A) \\ = 1*0.5*0.5*0.5+0.5*0.5*0.5*0.5+0.5*0.5*0.5*0.5+0*0.5*0.5*0.5 \\ =0.25 P(D∣¬A)∗P(¬A)=P(D∣BC)∗P(B∣¬A)P(C∣¬A)∗P(¬A)+P(D∣¬BC)∗P(¬B∣¬A)P(C∣¬A)∗P(¬A)+P(D∣B¬C)∗P(B∣¬A)P(¬C∣¬A)∗P(¬A)+P(D∣¬B¬C)∗P(¬B∣¬A)P(¬C∣¬A)∗P(¬A)=1∗0.5∗0.5∗0.5+0.5∗0.5∗0.5∗0.5+0.5∗0.5∗0.5∗0.5+0∗0.5∗0.5∗0.5=0.25
P ( D ) = P ( D ∣ A ) ∗ P ( A ) + P ( D ∣ ¬ A ) ∗ P ( ¬ A ) = 0.75 P ( A ∣ D ) = 0.5 0.75 = 2 3 P(D)=P(D|A)*P(A) +P(D|¬A)*P(¬A)=0.75 \\ P(A|D)= \frac {0.5} {0.75}= \frac {2} {3} P(D)=P(D∣A)∗P(A)+P(D∣¬A)∗P(¬A)=0.75P(A∣D)=0.750.5=32
另:关于P(D|A) 的证明:
P ( D ∣ A ) = P ( A D ) P ( A ) P ( A D ) = P ( A D B C ) + P ( A D B ¬ C ) + P ( A D ¬ B C ) + P ( A D ¬ B ¬ C ) P ( A D B C ) = P ( D ∣ B C ) P ( B ∣ A ) P ( C ∣ A ) P ( A ) P ( A D B ¬ C ) = P ( D ∣ B ¬ C ) P ( B ∣ A ) P ( ¬ C ∣ A ) P ( A ) P ( A D ¬ B C ) = P ( D ∣ ¬ B C ) P ( ¬ B ∣ A ) P ( C ∣ A ) P ( A ) P ( A D ¬ B ¬ C ) = P ( D ∣ ¬ B ¬ C ) P ( ¬ B ∣ A ) P ( ¬ C ∣ A ) P ( A ) 所以 P ( D ∣ A ) = P ( D ∣ B C ) P ( B ∣ A ) P ( C ∣ A ) P ( A ) + P ( D ∣ B ¬ C ) P ( B ∣ A ) P ( ¬ C ∣ A ) P ( A ) + P ( D ∣ ¬ B C ) P ( ¬ B ∣ A ) P ( C ∣ A ) P ( A ) + P ( D ∣ ¬ B ¬ C ) P ( ¬ B ∣ A ) P ( ¬ C ∣ A ) P ( A ) P ( A ) = P ( D ∣ B C ) P ( B ∣ A ) P ( C ∣ A ) + P ( D ∣ B ¬ C ) P ( B ∣ A ) P ( ¬ C ∣ A ) + P ( D ∣ ¬ B C ) P ( ¬ B ∣ A ) P ( C ∣ A ) + P ( D ∣ ¬ B ¬ C ) P ( ¬ B ∣ A ) P ( ¬ C ∣ A ) P(D|A) = \frac {P(AD)}{P(A)}\\ P(AD)=P(ADBC)+P(ADB¬C)+P(AD¬BC)+P(AD¬B¬C) \\ P(ADBC)=P(D|BC)P(B|A)P(C|A)P(A) \\ P(ADB¬C)=P(D|B¬C)P(B|A)P(¬C|A)P(A) \\ P(AD¬BC)=P(D|¬BC)P(¬B|A)P(C|A)P(A) \\ P(AD¬B¬C)=P(D|¬B¬C)P(¬B|A)P(¬C|A)P(A) \\ 所以P(D|A)=\frac {P(D|BC)P(B|A)P(C|A)P(A)+P(D|B¬C)P(B|A)P(¬C|A)P(A)+P(D|¬BC)P(¬B|A)P(C|A)P(A)+P(D|¬B¬C)P(¬B|A)P(¬C|A)P(A)}{P(A)} \\ = P(D|BC)P(B|A)P(C|A)+P(D|B¬C)P(B|A)P(¬C|A)+P(D|¬BC)P(¬B|A)P(C|A)+P(D|¬B¬C)P(¬B|A)P(¬C|A) P(D∣A)=P(A)P(AD)P(AD)=P(ADBC)+P(ADB¬C)+P(AD¬BC)+P(AD¬B¬C)P(ADBC)=P(D∣BC)P(B∣A)P(C∣A)P(A)P(ADB¬C)=P(D∣B¬C)P(B∣A)P(¬C∣A)P(A)P(AD¬BC)=P(D∣¬BC)P(¬B∣A)P(C∣A)P(A)P(AD¬B¬C)=P(D∣¬B¬C)P(¬B∣A)P(¬C∣A)P(A)所以P(D∣A)=P(A)P(D∣BC)P(B∣A)P(C∣A)P(A)+P(D∣B¬C)P(B∣A)P(¬C∣A)P(A)+P(D∣¬BC)P(¬B∣A)P(C∣A)P(A)+P(D∣¬B¬C)P(¬B∣A)P(¬C∣A)P(A)=P(D∣BC)P(B∣A)P(C∣A)+P(D∣B¬C)P(B∣A)P(¬C∣A)+P(D∣¬BC)P(¬B∣A)P(C∣A)+P(D∣¬B¬C)P(¬B∣A)P(¬C∣A)
ANSWER:

2.不确定性的量化
某学校,所有的男生都穿裤子,而女生当中,一半穿裤子,一半穿裙子。男女比例70%的可能性是4:6,有20%可能性是1:1,有10%可能性是6:4,问一个穿裤子的人是男生的概率有多大?
解:裤子-Trousers;裙子-Skirt;男生-Man;女生-Woman;
已知:
P(T|M)=1,P(T|W)=0.5,P(S|W)=0.5P(M/W=4/6)=0.7,P(M/W=1/1)=0.2,P(M/W=6/4)=0.1
求:P(M|T)
(1)错解1
P ( M ∣ T ) = P ( T ∣ M ) ∗ P ( M ) P ( T ) P ( T ) = P ( T ∣ M ) ∗ P ( M ) + P ( T ∣ W ) ∗ P ( W ) P(M|T)= \frac {P(T|M)*P(M)} {P(T)} \\ P(T)=P(T|M)*P(M)+P(T|W)*P(W) P(M∣T)=P(T)P(T∣M)∗P(M)P(T)=P(T∣M)∗P(M)+P(T∣W)∗P(W)
P ( M ) = 0.7 ∗ 0.4 + 0.2 ∗ 0.5 + 0.1 ∗ 0.6 = 0.44 P ( W ) = 0.7 ∗ 0.6 + 0.2 ∗ 0.5 + 0.1 ∗ 0.4 = 0.56 P(M)=0.7*0.4+0.2*0.5+0.1*0.6=0.44 \\ P(W)=0.7*0.6+0.2*0.5+0.1*0.4=0.56 P(M)=0.7∗0.4+0.2∗0.5+0.1∗0.6=0.44P(W)=0.7∗0.6+0.2∗0.5+0.1∗0.4=0.56
P ( T ∣ M ) ∗ P ( M ) = 1 ∗ 0.44 = 0.44 P ( T ) = 1 ∗ 0.44 + 0.5 ∗ 0.56 = 0.72 P ( M ∣ T ) = 0.44 0.72 = 0.611 P(T|M)*P(M)=1*0.44=0.44 \\ P(T)=1*0.44+0.5*0.56=0.72 \\ P(M|T) = \frac {0.44} {0.72}=0.611 P(T∣M)∗P(M)=1∗0.44=0.44P(T)=1∗0.44+0.5∗0.56=0.72P(M∣T)=0.720.44=0.611
(2)错解2
来源:QCNH雨文-人工智能作业三

(3)正解
来源:HNU岳麓山大小姐-人工智能导论:清览作业
①情况h1:男女比例4:6(P=0.7)
P 1 = P ( M ∣ T ) = P ( T ∣ M ) ∗ P ( M ) P ( T ) = 1 ∗ 0.4 P ( T ∣ M ) ∗ P ( M ) + P ( T ∣ W ) ∗ P ( W ) = 0.4 1 ∗ 0.4 + 0.5 ∗ 0.6 = 4 7 P_{1}=P(M|T)= \frac {P(T|M)*P(M)} {P(T)} \\ =\frac {1*0.4} {P(T|M)*P(M)+P(T|W)*P(W)} \\ = \frac {0.4} {1*0.4+0.5*0.6}=\frac {4} {7} P1=P(M∣T)=P(T)P(T∣M)∗P(M)=P(T∣M)∗P(M)+P(T∣W)∗P(W)1∗0.4=1∗0.4+0.5∗0.60.4=74
②情况h2:男女比例1:1(P=0.2)
P 2 = P ( M ∣ T ) = P ( T ∣ M ) ∗ P ( M ) P ( T ∣ M ) ∗ P ( M ) + P ( T ∣ W ) ∗ P ( W ) = 1 ∗ 0.5 1 ∗ 0.5 + 0.5 ∗ 0.5 = 2 3 P_{2}=P(M|T)=\frac {P(T|M)*P(M)} {P(T|M)*P(M)+P(T|W)*P(W)} \\ = \frac {1*0.5} {1*0.5+0.5*0.5}=\frac {2} {3} P2=P(M∣T)=P(T∣M)∗P(M)+P(T∣W)∗P(W)P(T∣M)∗P(M)=1∗0.5+0.5∗0.51∗0.5=32
③情况h3:男女比例6:4(P=0.1)
P 3 = P ( M ∣ T ) = P ( T ∣ M ) ∗ P ( M ) P ( T ∣ M ) ∗ P ( M ) + P ( T ∣ W ) ∗ P ( W ) = 1 ∗ 0.6 1 ∗ 0.6 + 0.5 ∗ 0.4 = 3 4 P_{3}=P(M|T)=\frac {P(T|M)*P(M)} {P(T|M)*P(M)+P(T|W)*P(W)} \\ = \frac {1*0.6} {1*0.6+0.5*0.4}=\frac {3} {4} P3=P(M∣T)=P(T∣M)∗P(M)+P(T∣W)∗P(W)P(T∣M)∗P(M)=1∗0.6+0.5∗0.41∗0.6=43
④MAP-极大后验概率
极大后验概率:选择概率最大的那个当作结果
h M A P = a r g m a x h ∈ H P ( D ∣ h ) P ( h ) = a r g m a x { P 1 ∗ P ( h 1 ) , P 2 ∗ P ( h 2 ) , P 3 ∗ P ( h 3 ) } = a r g m a x { 4 7 ∗ 7 10 , 2 3 ∗ 2 10 , 3 4 ∗ 1 10 } = a r g m a x { 4 10 , 4 30 , 3 40 } = 0.4 h_{MAP}=arg \space max_{h∈H} P(D|h)P(h) \\ = arg \space max \{ P_{1}*P(h_{1}),P_{2}*P(h_{2}),P_{3}*P(h_{3}) \} \\ =arg\space max \{ \frac {4} {7}* \frac {7} {10},\frac {2} {3}* \frac {2} {10},\frac {3} {4}* \frac {1} {10} \} \\ = arg\space max \{ \frac {4} {10},\frac {4} {30},\frac {3} {40}\} = 0.4 hMAP=arg maxh∈HP(D∣h)P(h)=arg max{ P1∗P(h1),P2∗P(h2),P3∗P(h3)}=arg max{ 74∗107,32∗102,43∗101}=arg max{ 104,304,403}=0.4
ANSWER:

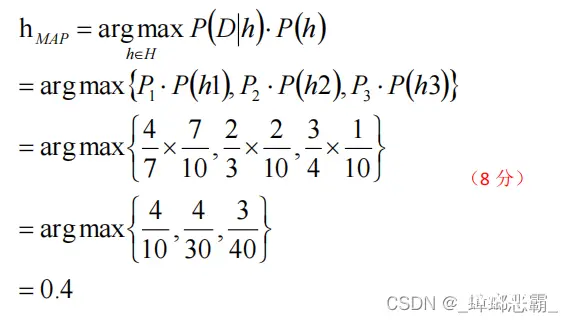
3.决策树
设样本集合如下表格,其中A、B、C是F的属性,请根据信息增益标准(ID3算法),画出F的决策树。
l o g 2 ( 2 / 3 ) = − 0.5842 l o g 2 ( 1 / 3 ) = − 1.5850 l o g 2 ( 3 / 4 ) = − 0.41504 log_{2} (2/3) = -0.5842 \\ log_{2} ( 1/3) = -1.5850 \\ log_{2} (3/4) = -0.41504 log2(2/3)=−0.5842log2(1/3)=−1.5850log2(3/4)=−0.41504
| A | B | C | F |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
解:
①第一次分类
计算A、B、C的熵:
H A = 4 7 H A = 0 + 3 7 H A = 1 = − 1 7 ( 2 ∗ l o g 2 2 4 + 2 ∗ l o g 2 2 4 + 1 ∗ l o g 2 1 3 + 2 ∗ l o g 2 2 3 ) = 0.965 H_{A}=\frac {4} {7}H_{A=0}+\frac {3} {7}H_{A=1} \\ = -\frac {1} {7} (2*log_{2} \frac {2} {4}+2*log_{2} \frac {2} {4}+1*log_{2} \frac {1} {3}+2*log_{2} \frac {2} {3}) \\ = 0.965 HA=74HA=0+73HA=1=−71(2∗log242+2∗log242+1∗log231+2∗log232)=0.965
H B = 4 7 H B = 0 + 3 7 H B = 1 = − 1 7 ( 1 ∗ l o g 2 1 4 + 3 ∗ l o g 2 3 4 + 2 ∗ l o g 2 2 3 + 1 ∗ l o g 2 1 3 ) = 0.857 H_{B}=\frac {4} {7}H_{B=0}+\frac {3} {7}H_{B=1} \\ = -\frac {1} {7} (1*log_{2} \frac {1} {4}+3*log_{2} \frac {3} {4}+2*log_{2} \frac {2} {3}+1*log_{2} \frac {1} {3}) \\ = 0.857 HB=74HB=0+73HB=1=−71(1∗log241+3∗log243+2∗log232+1∗log231)=0.857
H C = 4 7 H C = 0 + 3 7 H C = 1 = − 1 7 ( 3 ∗ l o g 2 3 4 + 1 ∗ l o g 2 1 4 + 0 ∗ l o g 2 0 3 + 3 ∗ l o g 2 3 3 ) = 0.464 H_{C}=\frac {4} {7}H_{C=0}+\frac {3} {7}H_{C=1} \\ = -\frac {1} {7} (3*log_{2} \frac {3} {4}+1*log_{2} \frac {1} {4}+0*log_{2} \frac {0} {3}+3*log_{2} \frac {3} {3}) \\ = 0.464 HC=74HC=0+73HC=1=−71(3∗log243+1∗log241+0∗log230+3∗log233)=0.464
属性C的熵最低,故选择C。
C=1时:F=1,熵为0;【确定C的右子树】C=0时:对其4个例子再进行第二次分类:
②第二次分类(C=0)
H A = 2 4 H A = 0 + 2 4 H A = 1 = − 1 4 ( 2 ∗ l o g 2 2 2 + 0 ∗ l o g 2 0 2 + 1 ∗ l o g 2 1 2 + 1 ∗ l o g 2 1 2 ) = 0.5 H_{A}=\frac {2} {4}H_{A=0}+\frac {2} {4}H_{A=1} \\ = -\frac {1} {4} (2*log_{2} \frac {2} {2}+0*log_{2} \frac {0} {2}+1*log_{2} \frac {1} {2}+1*log_{2} \frac {1} {2}) \\ = 0.5 HA=42HA=0+42HA=1=−41(2∗log222+0∗log220+1∗log221+1∗log221)=0.5
H B = 2 4 H B = 0 + 2 4 H B = 1 = − 1 4 ( 1 ∗ l o g 2 1 2 + 1 ∗ l o g 2 1 2 + 2 ∗ l o g 2 2 2 + 0 ∗ l o g 2 0 2 ) = 0.5 H_{B}=\frac {2} {4}H_{B=0}+\frac {2} {4}H_{B=1} \\ = -\frac {1} {4} (1*log_{2} \frac {1} {2}+1*log_{2} \frac {1} {2}+2*log_{2} \frac {2} {2}+0*log_{2} \frac {0} {2}) \\ = 0.5 HB=42HB=0+42HB=1=−41(1∗log221+1∗log221+2∗log222+0∗log220)=0.5
属性A/B的熵相同,故选择A/B均可。
如果选择A:
A=0时:F=0,熵为0;【确定A的左子树】A=1时:对其2个例子再按照属性B分类;
如果选择B:
B=1时:F=0,熵为0;【确定B的右子树】B=0时:对其2个例子再按照属性A分类;
③第三次分类(A=1)【决策树1】
H B = 1 2 H B = 0 + 1 2 H B = 1 = − 1 2 ( 0 ) = 0 H_{B}=\frac {1} {2}H_{B=0}+\frac {1} {2}H_{B=1} \\ = -\frac {1} {2} (0) = 0 HB=21HB=0+21HB=1=−21(0)=0
其实到这里:
B=0时:F=1,熵为0;【确定B的左子树】B=1时:F=0,熵为0;【确定B的右子树】;
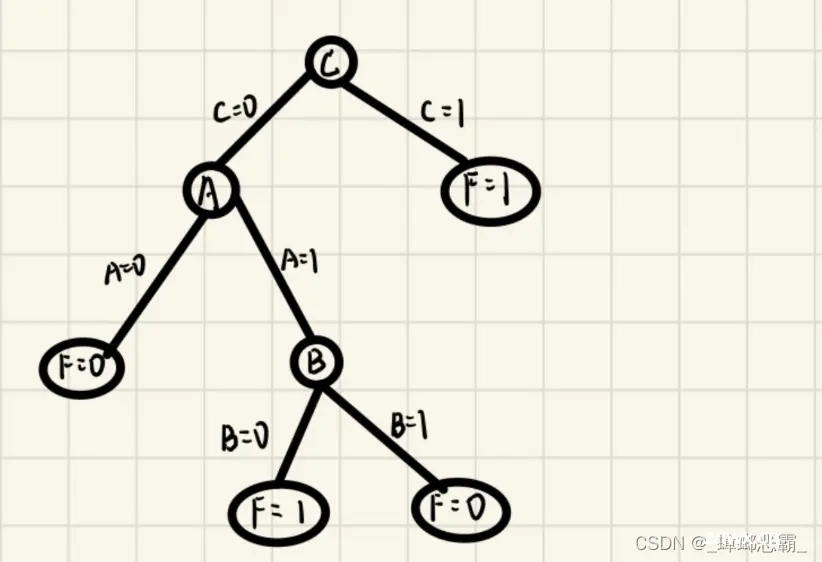
④第三次分类(B=0)【决策树2】
H A = 1 2 H A = 0 + 1 2 H A = 1 = − 1 2 ( 0 ) = 0 H_{A}=\frac {1} {2}H_{A=0}+\frac {1} {2}H_{A=1} \\ = -\frac {1} {2} (0) = 0 HA=21HA=0+21HA=1=−21(0)=0
其实到这里:
A=0时:F=0,熵为0;【确定A的左子树】A=1时:F=1,熵为0;【确定A的右子树】;
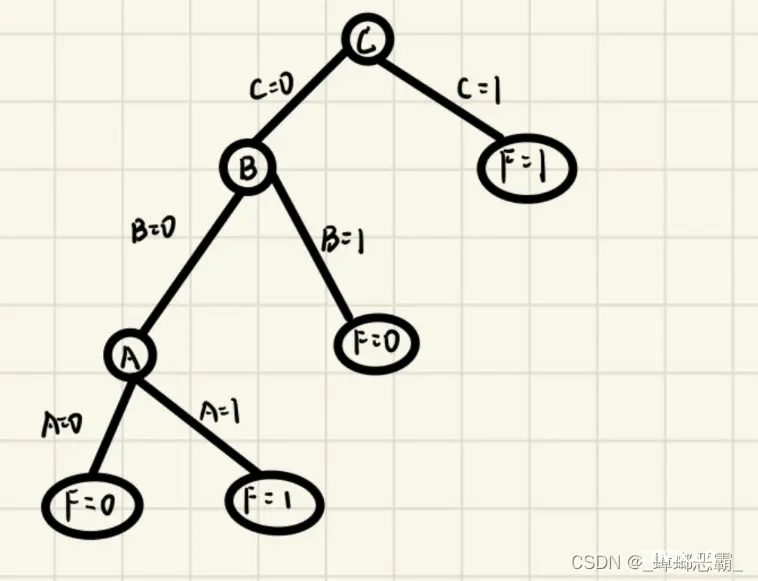
ANSWER:

4.人工神经网络
阈值感知器可以用来执行很多逻辑函数,说明它对二进制逻辑函数与(AND)和或(OR)的实现过程。
(1)与(AND)
真值表| x1 | x2 | x1 AND x2 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
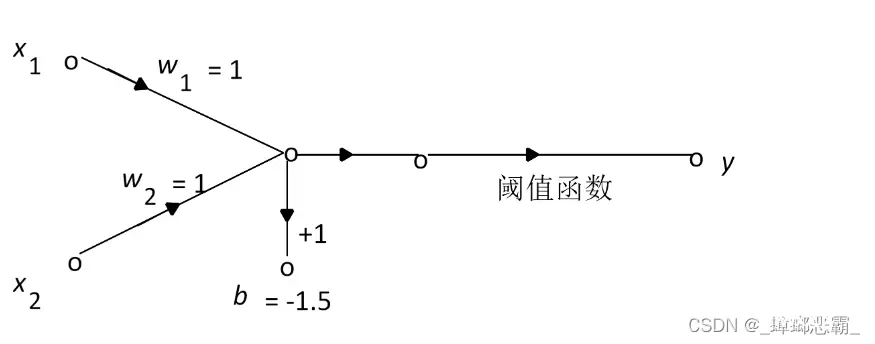
感知器算法

算法实现(1)初始化
设定初始的权值w1,w2和阈值bias;
class Perceptron(object): def __init__(self, num, activator): ''' 初始化感知器,设置输入参数的个数,以及激活函数。 激活函数的类型为double -> double ''' self.activator = activator #权重向量初始化为 0 self.weights = [0.0 for _ in range(num)] self.bias = 0 (2)计算激活函数值 根据输入x1( p), x2( p),…, xn( p) 和权值w1,w2,…,wn计算输出Y( p),其中p表示迭代的轮数
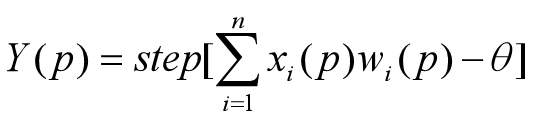
可以把下面的bias看做 -θactivator即step函数
def predict(self, input_vec): ''' 输入向量,输出感知器的计算结果 ''' # 利用map函数计算[x1*w1, x2*w2, x3*w3], 然后转化为列表 # 最后利用 sum 求和 return self.activator( sum( list( map( lambda x, y: x*y, self.weights, input_vec ) ) ) + self.bias ) #return self.activator(sum(tmp))
(3)更新权值
计算公式

实现
def _update_weights(self, input_vec, output, label, rate): '''' 按照感知器规则,更新权重 ''' delta = label - output self.weights = list( map( lambda x, y: x + y*rate*delta, self.weights, input_vec ) ) self.bias += rate * delta
(4)迭代循环
def _one_iteration(self, input_vecs, labels, rate): ''' 一次迭代,把所有的训练数据过一遍 ''' # 把输入和输出打包在一起,成为样本的列表[(input_vec, label), ...] # 而每个训练样本是(input_vec, label) samples = zip(input_vecs, labels) # 对于每个样本,按照感知器规则更新权重 for input_vec, label in samples: output = self.predict(input_vec) self._update_weights(input_vec, output, label, rate) 完整实现

class Perceptron(object): def __init__(self, num, activator): ''' 初始化感知器,设置输入参数的个数,以及激活函数。 激活函数的类型为double -> double ''' self.activator = activator #权重向量初始化为 0 self.weights = [0.0 for _ in range(num)] self.bias = 0 def __str__(self): ''' 打印学习到的权重、偏置项bias ''' return 'weight: %s\n bias: %f\n' % (self.weights, self.bias) def __print__(self): print('weight: %s\n bias: %f\n' % (self.weights, self.bias)) def predict(self, input_vec): ''' 输入向量,输出感知器的计算结果 ''' # 利用map函数计算[x1*w1, x2*w2, x3*w3], 然后转化为列表 # 最后利用 sum 求和 return self.activator( sum( list( map( lambda x, y: x*y, self.weights, input_vec ) ) ) + self.bias ) #return self.activator(sum(tmp)) def train(self, input_vecs, labels, iterations, rate): ''' 输入训练数据:一组向量、与每个向量对应的label;以及训练轮数、学习率 ''' i=0 for _ in range(iterations): print("迭代次数:{}".format(i)) i+=1 self.__print__() self._one_iteration(input_vecs, labels, rate) def _one_iteration(self, input_vecs, labels, rate): ''' 一次迭代,把所有的训练数据过一遍 ''' # 把输入和输出打包在一起,成为样本的列表[(input_vec, label), ...] # 而每个训练样本是(input_vec, label) samples = zip(input_vecs, labels) # 对于每个样本,按照感知器规则更新权重 for input_vec, label in samples: output = self.predict(input_vec) self._update_weights(input_vec, output, label, rate) def _update_weights(self, input_vec, output, label, rate): '''' 按照感知器规则,更新权重 ''' delta = label - output self.weights = list( map( lambda x, y: x + y*rate*delta, self.weights, input_vec ) ) self.bias += rate * delta'''' 以下代码为实现 and 函数'''def activate(x): if x > 0: return 1 return 0def get_train_dataset(): #构建训练数据 input_vecs = [ [0, 0], [0, 1], [1, 0], [1, 1] ] #训练数据 labels = [0, 0, 0, 1] #输出列表 return input_vecs, labelsdef train_data(): # 创建一个感知器 perceptron = Perceptron(2, activate) input_vecs, labels = get_train_dataset() # 训练数据,然后迭代 20 轮,学习速率为 0.1 perceptron.train(input_vecs, labels, 20, 0.1) return perceptronresult = train_data()print(result)#测试真值表print('1 and 1 = %d' % result.predict([1, 1]))print('0 and 0 = %d' % result.predict([0, 0]))print('1 and 0 = %d' % result.predict([1, 0]))print('0 and 1 = %d' % result.predict([0, 1]))
ANSWER:

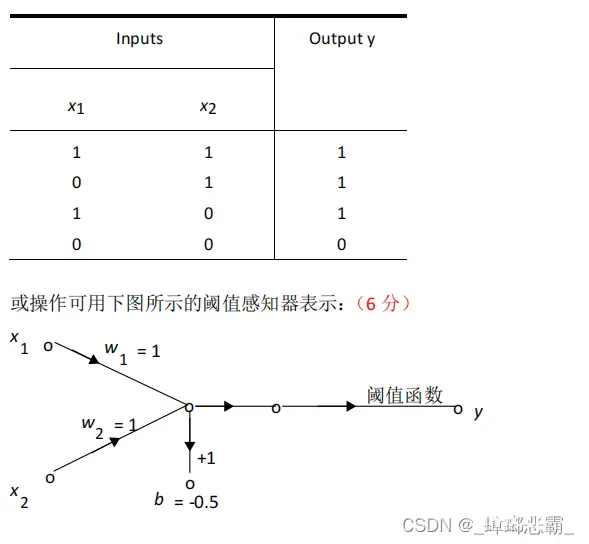
(2)或(OR)
真值表| x1 | x2 | x1 OR x2 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
设y=w1*x1+w2*x2+b,阈值函数用的Step函数

与AND的实现类似:
class Perceptron(object): def __init__(self, num, activator): ''' 初始化感知器,设置输入参数的个数,以及激活函数。 激活函数的类型为double -> double ''' self.activator = activator #权重向量初始化为 0 self.weights = [0.0 for _ in range(num)] self.bias = 0 def __str__(self): ''' 打印学习到的权重、偏置项bias ''' return 'weight: %s\n bias: %f\n' % (self.weights, self.bias) def predict(self, input_vec): ''' 输入向量,输出感知器的计算结果 ''' # 利用map函数计算[x1*w1, x2*w2, x3*w3], 然后转化为列表 # 最后利用 sum 求和 return self.activator( sum( list( map( lambda x, y: x*y, self.weights, input_vec ) ) ) + self.bias ) #return self.activator(sum(tmp)) def train(self, input_vecs, labels, iterations, rate): ''' 输入训练数据:一组向量、与每个向量对应的label;以及训练轮数、学习率 ''' for _ in range(iterations): self._one_iteration(input_vecs, labels, rate) def _one_iteration(self, input_vecs, labels, rate): ''' 一次迭代,把所有的训练数据过一遍 ''' # 把输入和输出打包在一起,成为样本的列表[(input_vec, label), ...] # 而每个训练样本是(input_vec, label) samples = zip(input_vecs, labels) # 对于每个样本,按照感知器规则更新权重 for input_vec, label in samples: output = self.predict(input_vec) self._update_weights(input_vec, output, label, rate) def _update_weights(self, input_vec, output, label, rate): '''' 按照感知器规则,更新权重 ''' delta = label - output self.weights = list( map( lambda x, y: x + y*rate*delta, self.weights, input_vec ) ) self.bias += rate * delta'''' 以下代码为实现 and 函数'''def activate(x): if x > 0: return 1 return 0def get_train_dataset(): #构建训练数据 input_vecs = [ [0, 0], [0, 1], [1, 0], [1, 1] ] #训练数据 labels = [0, 1, 1, 1] #输出列表 return input_vecs, labelsdef train_data(): # 创建一个感知器 perceptron = Perceptron(2, activate) input_vecs, labels = get_train_dataset() # 训练数据,然后迭代 20 轮,学习速率为 0.1 perceptron.train(input_vecs, labels, 20, 0.1) return perceptronresult = train_data()print(result)#测试真值表print('1 or 1 = %d' % result.predict([1, 1]))print('0 or 0 = %d' % result.predict([0, 0]))print('1 or 0 = %d' % result.predict([1, 0]))print('0 or 1 = %d' % result.predict([0, 1]))
ANSWER:
5.深度学习
深度学习的原理是什么?以一个典型的深度学习算法为例进行说明。
深度学习的原理
深度学习是一种机器学习方法,它试图通过模拟人类大脑的神经网络结构来实现智能任务的自动化。其原理基于神经网络的概念,其中包含了多个层次的神经元,每一层都会对输入数据进行一系列非线性变换和特征提取,最终输出一个结果。
举例-卷积神经网络(Convolutional Neural Network,CNN)
卷积层(Convolutional Layer):CNN中的核心部分。 使用一组可学习的滤波器(也称为卷积核)对输入数据进行卷积操作。通过滑动窗口的方式在输入数据上进行滤波操作,提取输入数据中的特征。每个滤波器会检测输入数据中的某种特定模式或特征。 激活函数(Activation Function): 卷积操作得到的结果会被输入到激活函数中,以引入非线性特性。常用的激活函数包括ReLU(Rectified Linear Unit)、Sigmoid、Tanh等,能在网络中引入非线性,使得神经网络能够学习到更加复杂的模式和特征。 池化层(Pooling Layer):减少特征图的空间尺寸,保留重要的特征信息。 常见的池化操作:最大池化(Max Pooling)和平均池化(Average Pooling)。通过减小特征图的尺寸,池化层能够降低模型的参数数量,提高模型的计算效率。 全连接层(Fully Connected Layer): 经过一系列的卷积层和池化层之后,通常会将特征图展平为一维向量,并输入到全连接层中。全连接层中的每个神经元都与前一层中的所有神经元相连,它们通过学习权重来将高层的特征表示映射到输出类别。 损失函数(Loss Function):衡量模型的预测输出与真实标签之间的差异。 常见的损失函数:交叉熵损失函数(Cross-Entropy Loss)和均方误差损失函数(Mean Squared Error Loss)等。 优化算法(Optimization Algorithm):用于更新模型参数,使得损失函数的值尽可能地减小。 常用的优化算法包括随机梯度下降(Stochastic Gradient Descent,SGD)及其改进算法,如Adam、RMSProp等。
通过不断地反向传播误差并更新参数,深度学习模型能够逐渐优化自身的性能,从而实现对复杂数据的高效处理和学习。
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。