文章目录

[发表博客之：int8 量化 原理讲解，AI推理工程师必备技能！](https://cyj666.blog.csdn.net/article/details/138426588)

发表博客之：int8 量化 原理讲解，AI推理工程师必备技能！

如果你在找工作，你必须看我这篇文章！！

模型推理的时候，为了降低时延，通常会采用int8量化。那么为啥int8量化这个技术会带来收益呢？

首先下面这个图是某个模型的matmul op。其中两个输入都是fp32，输出也是fp32。由于是用fp32精度来计算的，因此肯定比较费时间的！

而int8量化时，其实就是在上面图的基础上，分别在matmul的两个输入上面，成对的插入了QDQ算子！变成下面这张图这样！

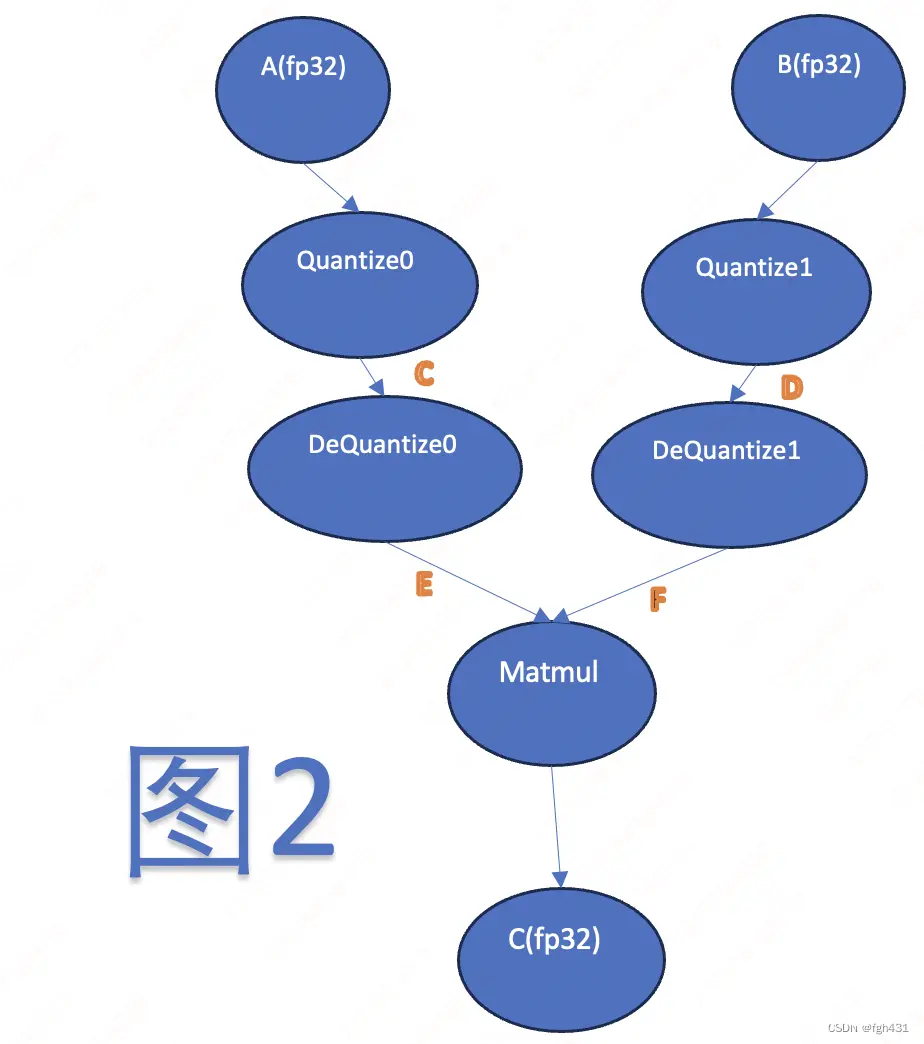
有人可能疑惑了，你把模型上插入了两对QDQ算子，你怎么保证图2和图1是等价的呢？其实啊，图1和图2未必是完全一样的，

但是只要保证图2和图1最后使得模型总体的效果是一样的就行了，这个不是推理工程师的事情，保证模型效果一样是压缩工程师的事情！压缩工程师会保证插入QDQ之后的模型效果仍然很棒！如果不能保证，那这个就是压缩工程师的锅！

继续看图2。<code>Quantize 算子就是将 fp32 的输入量化到int8，而 DeQuantize 算子就是将int8的输入反量化到fp32。Quantize 算子有两个输入，一个是fp32的输入

x

x

x，另一个就是scale参数，输出是int8类型的数据。

它的作用就是将fp32的输入，按照scale参数，量化到int8。公式是用

x

x

x除以scale参数，然后四舍五入取整，最后clip到-127到127之间当然啦，细节啥的不重要。 那DeQuantize算子有两个输入，一个是int8的输入

x

x

x，另一个也是scale参数，算子的输出是fp32类型

就是将int8的输入，反量化到fp32。具体公式就是用int8的数字

x

x

x，乘以 scale参数即可！也就是DeQuantize算子其实就是个乘法而已啊！很平平无奇！

继续看图2。DeQuantize0 和 DeQuantize1 的输出都是fp32数字，从而和MatMul算子的两个输入都是fp32。那我这个Matmul还是用fp32精度计算啊！这能有个毛线的加速啊！因此需要对图2进行一定的等价变换！

继续看图2。一般而言，Matmul的第1个输入正常是个输入，输入是个

[

M

,

K

]

[M,K]

[M,K]的tensor

另一个输入是权重，是个

[

K

,

N

]

[K,N]

[K,N]的权重tensor 一般而言，Quantize0和Dequantize0的scale参数是个单独的数字，也就是孤零零的一个数字！Quantize1和Dequantize1的scale参数是

N

N

N个数字，也就是每列共同拥有一个scale参数！

不同的列的scale参数是不一样的！哈哈，其实这个专业术语叫做per channel量化！ 而矩阵运算中，

M

a

t

m

u

l

O

u

t

[

i

,

j

]

=

∑

k

=

0

K

−

1

E

[

i

,

k

]

F

[

k

,

j

]

MatmulOut[i,j]=\sum_{k=0}^{K-1} E[i,k]F[k,j]

MatmulOut[i,j]=k=0∑K−1​E[i,k]F[k,j]，也就是

M

a

t

m

u

l

O

u

t

MatmulOut

MatmulOut中的每一个元素，是E的一行和F的一列进行乘加运算得到的！

而E的所有元素共享一个scale参数，F的一列也是共享一个scale参数的，因此可以把

E

E

E的scale参数和

F

F

F的scale都提出来！

这样

M

a

t

m

u

l

O

u

t

[

i

,

j

]

=

D

e

Q

u

a

n

t

i

z

e

0

s

c

a

l

e

∗

D

e

Q

u

a

n

t

i

z

e

1

s

c

a

l

e

[

j

]

∑

k

=

0

K

−

1

C

[

i

,

k

]

D

[

k

,

j

]

MatmulOut[i,j]=DeQuantize0_{scale} * DeQuantize1_{scale}[j] \sum_{k=0}^{K-1} C[i,k]D[k,j]

MatmulOut[i,j]=DeQuantize0scale​∗DeQuantize1scale​[j]k=0∑K−1​C[i,k]D[k,j]

D

e

Q

u

a

n

t

i

z

e

1

s

c

a

l

e

[

j

]

DeQuantize1_{scale}[j]

DeQuantize1scale​[j] 表示 DeQuantize1算子的scale参数的第j个元素！

也就是说，matmul的输出结果，完全可以先由

E

E

E和

F

F

F做矩阵乘法，

然后乘以

D

e

Q

u

a

n

t

i

z

e

0

s

c

a

l

e

∗

D

e

Q

u

a

n

t

i

z

e

1

s

c

a

l

e

[

j

]

DeQuantize0_{scale} * DeQuantize1_{scale}[j]

DeQuantize0scale​∗DeQuantize1scale​[j]得到！由此得到图3

其中 Dequantize2 的scale参数是由 <code>图2中DeQuantize0和DeQuantize1的scale参数相乘得到的！并且在图3中我们可以看到此时matmul的输入是int8啦！此时可以调用int8的matmul进行计算！

不过要注意，此时matmul的输出是int32数字哦！ 上面这个技术叫做

DQ 下移！欢迎大家点赞我！