人工智能原理及其应用---主观Bayes推理
轻舟行岸 2024-06-21 16:31:03 阅读 50
主观Bayes方法是解决标准Bayes公式所存在的需要由逆概率去求原概率的问题。
全概率公式如下:
设时间A1,A2,A3,…,An满足:
(1)任意两个事件都不相容,即当i≠j时,有Ai∩Aj=Φ(i=1,2,….,n;j=1,2,…,n)
(2)P(Ai)>0(i=1,2,…,n)
(3)样本空间D,对任何事件B有下式成立:
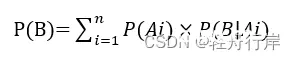
Bayes公式:
设事件A1,A2,…,An满足上面的条件,则对任何事物B有下式成立:
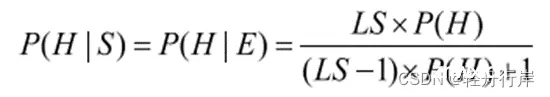
该定理称为Bayes定理,上式也称为Bayes公式。
将全概率公式代入Bayes公式,有:
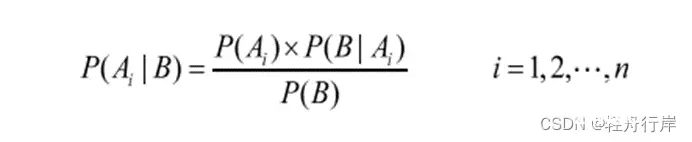
表示形式,在主观Bayes方法中,知识是用产生式表示的,形式为:
IF E THEN (LS,LN) H
其中,(LS,LN)表示该知识的知识强度,LS为充分性度量,LN为必要性度量。
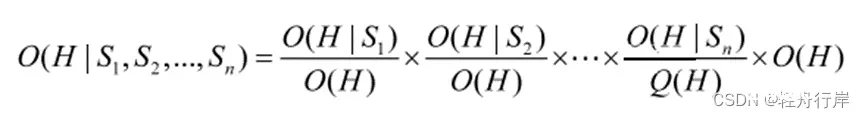
几率函数:
X的几率等于X出现的概率与X不出现的概率之比,且P(X)与O(X)的变化一致。
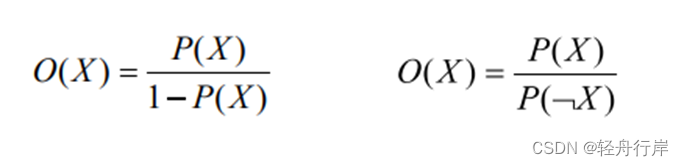
当E为真时,可以用LS将H的先验几率O(H)更新为其后验几率O(H|E)
当E为假时,可以用LN将H的先验几率O(H)更新为其后验几率O(H|﹁E)
LS与LN的关系
由于E和﹁E不会同时支持或同时排斥H,因此只有下面三种情况存在:
a) LS>1且LN<1
b) LS<1且LN>1
c) LS=LN=1
主观Bayes方法推理的任务:
根据E的概率P(E)及LS和LN的值,把H的先验概率P(H)或先验几率O(H)更新为后验概率或后验几率。
证据在当前观察下肯定为真时
当证据E肯定为真时,P(E)=P(E|S)=1。将H的先验几率更新为后验几率的公式为:O(H|E)=LS×O(H)
把H的先验概率P(H)更新为后验概率P(H|E)的公式,有
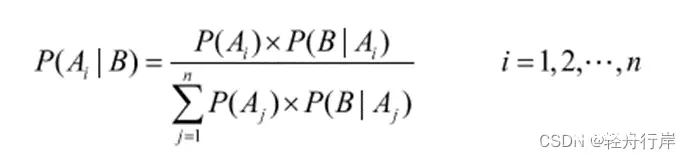
证据在当前观察下肯定为假时
当证据E肯定为假时,P(E)=P(E|S)=0,P(﹁E)=1。将H的先验几率更新为后验几率的公式为:O(H|﹁E)=LN×O(H)
把H的先验概率P(H)更新为后验概率P(H|﹁E)的公式,有
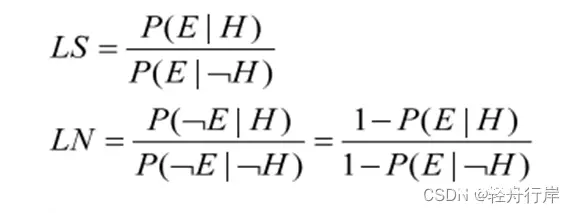
证据在当前观察下既非真又非假时
由杜达等人给出的公式有:
P(H|S)=P(H|E)×P(E|S)+P(H|﹁E)×P(﹁E|S)
a) P(E|S)=1
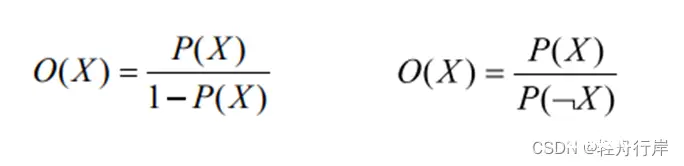
b) P(E|S)=0
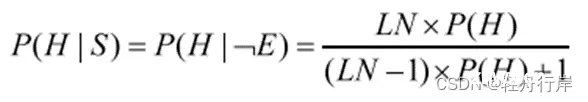
c) P(E|S)=P(E)
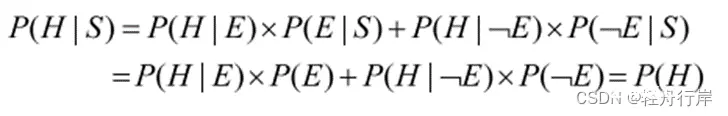
d) P(E|S)为其它值
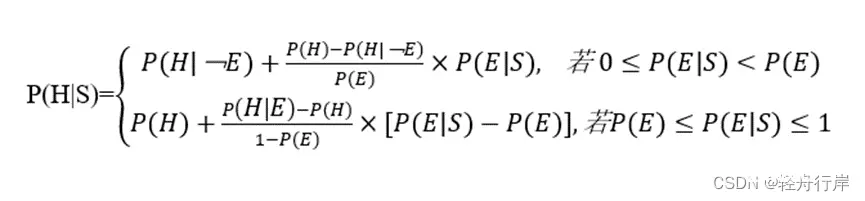
结论不确定性的合成
假设有n条知识都支持同一结论H,并且这些知识的前提条件分别是n个相互独立的证据E1,E2,…,En,而每个证据所对应的观察又分别是S1,S2,…,Sn。
求H的后验概率方法是:
a) 首先对每条知识分别求出H的后验几率O(H|Si)
b) 然后利用这些后验几率并按下述公式求出在所有观察下H的后验几率:
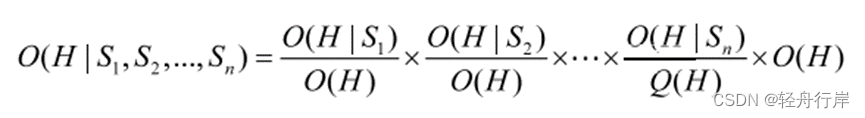
上一篇: 【腾讯云 HAI域探秘】释放生产力:基于 HAI 打造团队专属的 AI 编程助手
下一篇: 大数据毕业设计Python+Spark高速公路车流量预测可视化分析 智慧城市交通大数据 交通流量预测 交通爬虫 地铁客流量分析 深度学习 计算机毕业设计 知识图谱 深度学习 人工智能
本文标签
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。