0 前言

构建

读者需要具备的知识有：信息熵、条件熵、信息增益、信息增益比。
本文所使用的数据集为：西瓜数据集 1.2节。

1 C4.5算法流程

准备数据集：
输入数据集包含多个样本，每个样本具有多个特征（属性）和一个目标类别标签。
设置阈值：
初始化信息增益的阈值ε，用于决定何时停止树的生长。在决策树的构建过程中，对于每个节点，计算所有特征的信息增益。如果某个特征的信息增益大于或等于阈值ε，则使用该特征进行节点划分；否则，停止划分，并将该节点标记为叶节点。通过设定较高的阈值，可以限制决策树的生长，减少节点的数量，从而避免过拟合。本文并未设置阈值，感兴趣的读者可以自行实验。
选择最优属性：
从候选属性中选择信息增益率最高的属性作为当前节点的分裂属性。
分裂数据集：
根据选定的最优属性的不同取值，将数据集分割成若干个子集。
递归构建子树：
对每个子集，重复步骤3~4，直到满足以下任一条件为止：①子集中的所有样本都属于同一类别。②没有更多属性可以用于进一步划分（或剩余属性的信息增益率均低于阈值ε）。

2 例题

准备数据集：
见前言西瓜数据集。假设数据集为D。
设置阈值：
本文不考虑。
构建根节点、分割数据集：结果如下图(2-1)所示。
计算出除编号、好瓜外的其他特征的信息增益比gr(?,?)，发现gr(好瓜,纹理)的信息增益比为最大，将特征纹理作为根节点，将数据集D分割成3个子集，子集①：纹理为模糊，子集②：纹理为清晰，子集③：纹理为稍糊。当纹理为模糊时全是坏瓜，故需要设置'否'叶节点，其他情况有好瓜也有坏瓜，故应该继续构建分支。
若读者规定决策树构建必须有阈值ε，假设阈值ε=0.4000，可以看出已经计算的所有特征的信息增益均小于阈值，根据阈值构建算法，此时D1、D2均应该变成叶节点(叶节点的类别应设置为该分支的子数据集中占比最多的类)，读者是否会考虑该树太"简陋"了？所以阈值的设定很大程度上关系到决策树的准确性。
li>
递归构建图2-1的D1：结果如下图(2-2)所示。
计算除编号、好瓜、纹理外的其他特征的信息增益比gr(?,?)，发现有多个特征信息增益比同等大，默认选择第一个信息增益比最大的特征构建节点，同时分割数据集D1为若干个子集，根据子集数据去设置叶节点或继续构建分支。
li>
递归构建图2-2的D3：结果如下图(2-3)所示。
计算出特征色泽、敲声、脐部、触感的信息增益比，选择第一个最大信息增益比的特征色泽构建节点，并分割数据集D3为若干子集，并判断子集需要设置叶节点还是继续构建分支。构建决策树中途会出现某分支没有特定特征的样本，请阅读上图中的文字说明。
li>
递归构建图2-3的D4：结果如下图(2-4)所示。
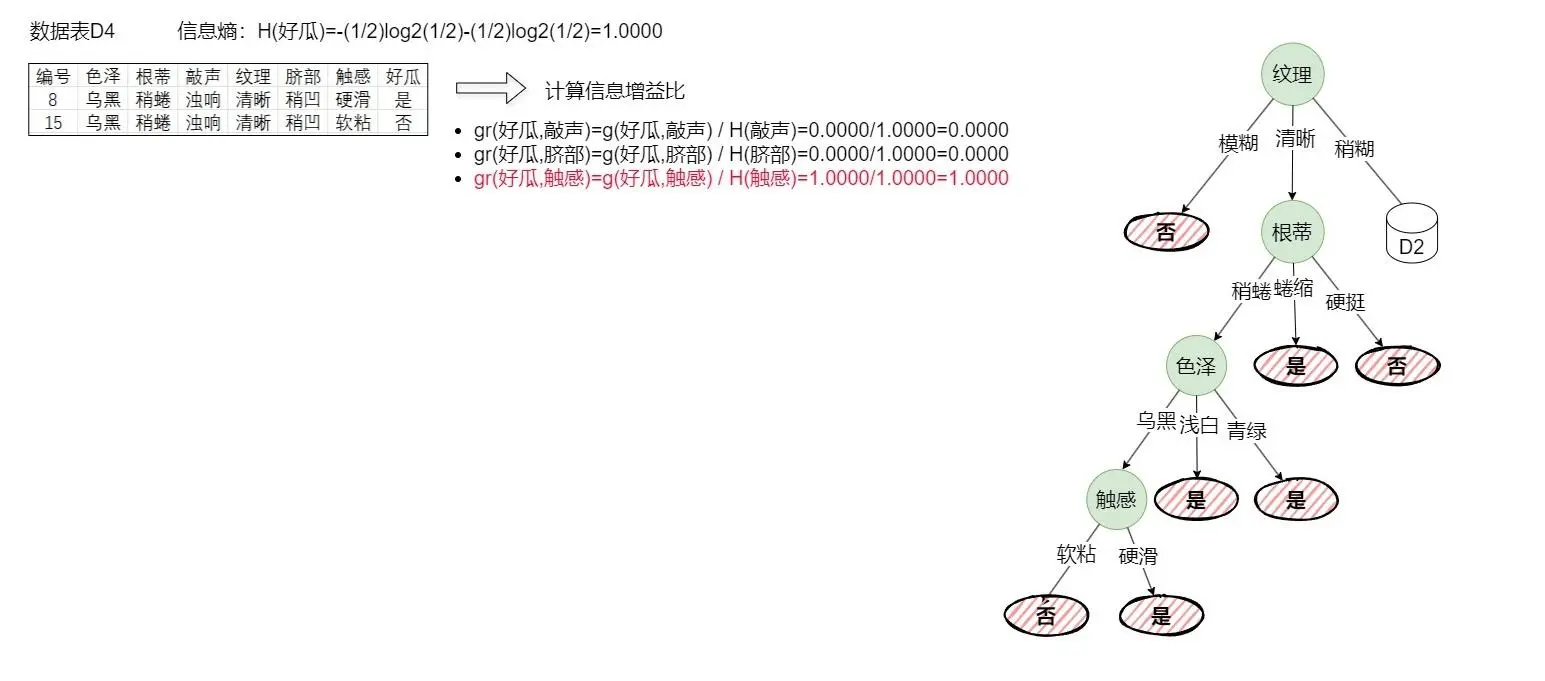
同样计算信息增益比，选择信息增益比最大的特征构建节点，同时分割数据集并构建分支。从上图可以看到已经没有样本继续构建，所以下一步应该构建D2。
li>
递归构建图2-4的D2：结果如下图(2-5)所示。
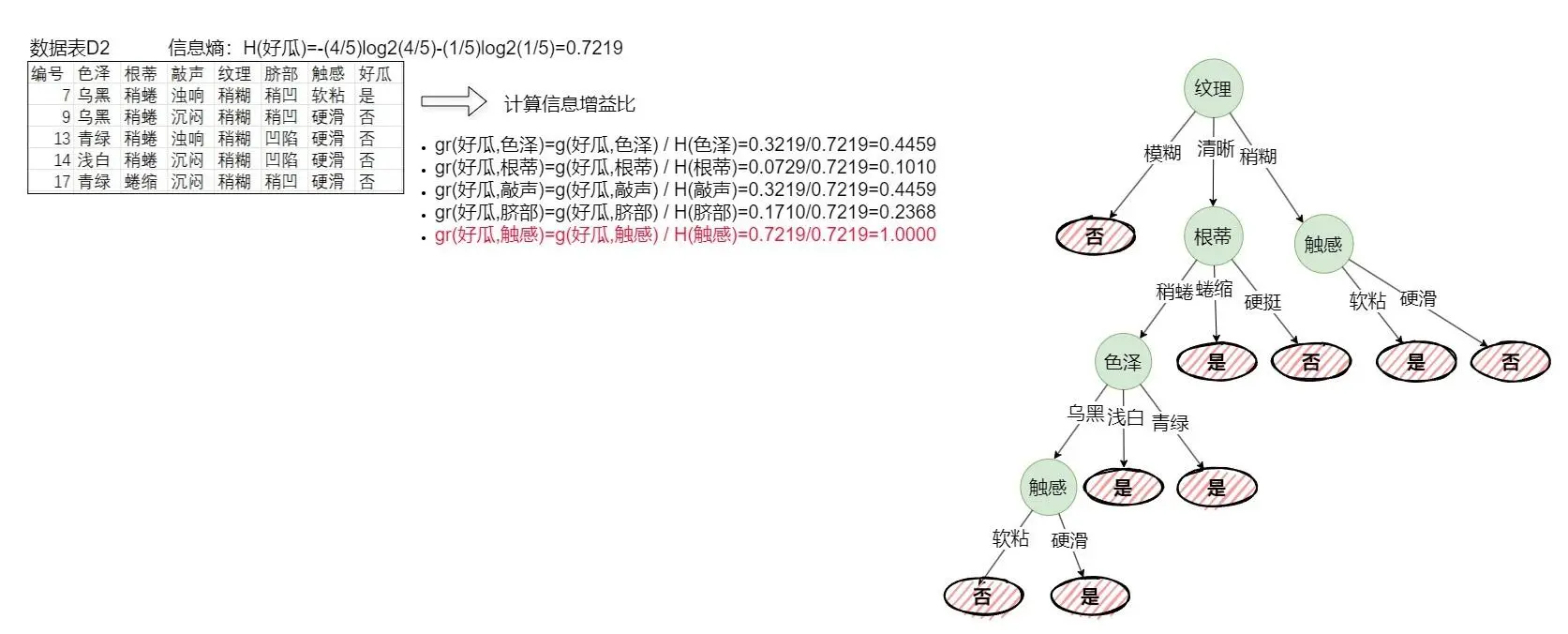
依次按照前文步算法骤，直到构建完成。
li>